涡轮机叶片同步振动参数辨识方法研究(建模仿真)

王维民， 任三群， 陈立芳， 黄 山

(北京化工大学 高端机械装备健康监控与治愈化北京市重点实验室, 北京 100029)

涡轮机叶片同步振动参数辨识方法研究(建模仿真)

王维民， 任三群， 陈立芳， 黄 山

(北京化工大学 高端机械装备健康监控与治愈化北京市重点实验室, 北京 100029)

基于叶尖定时非接触式叶片振动测量技术，提出一种需要较少传感器又能提高测量精度的叶片同步振动参数分析方法。通过低转速到高转速运行过程，测量出叶片振动位移随转频变化之间的关系，根据非线性最小二乘拟合算法获得叶片谐共振点处的中心频率、振动最大幅值、相位、振动恒偏量，但无法获得叶片振动倍频值。对谐共振动点附近处的频率值进行恒速运转，不同位置处的传感器获得不同的振动位移，通过GARIV算法获得各叶片在对应谐共振频率点处的倍频值，结合扫频拟合获得的叶片振动参数可做出叶片坎贝尔图。基于以上的识别方法，提出了叶尖计时传感器的布置方法，并对实际测量中可能存在的干扰因素进行了详细的仿真分析，验证了方法的可行性。该辨识方法的实验验证将在《涡轮机叶片同步振动参数辨识方法研究(实验研究)》一文中给出。

涡轮叶片； 同步振动； 参数辨识； 叶尖定时(BTT)； GARIV

叶尖计时测量法常被用于非接触式应力测量系统中以评估叶片的工作应力[1]。也可以被用于监测叶片和轮盘的工作状态，叶片振型预测以及阻尼比识别等[2]。该方法主要通过安装在机匣上的叶顶传感器监测叶片实际到达时间与理论到达时间的差值来获得叶片的振动情况。在研究涡轮叶片振动特性的过程中，主要分为异步振动和同步振动两种。同步振动较于异步振动而言，由于单支叶顶传感器在监测过程中监测到的叶片振动值不变，这对叶片振动参数辨识带来较大的难度，所以需要布置较多的传感器才能辨识出叶片的同步振动参数。但在实际的工程测量中，可安装的测点数量被严格的限制，进而言之使用较少的传感器来辨识叶片振动特性是非常有必要的。

叶片同步振动参数识别方法有双参数法[3-4]，但对噪声较为敏感，抗干扰较差。正弦曲线拟合法[5-6]，要求布置较多的传感器。单独使用GARIV方法时[7]，可获得叶片谐共振中心的频率值，但叶片振动幅值等参数的求取误差较大。文献[8]在正弦曲线拟合法的基础上提出了多传感器扫频拟合方法，虽然可以通过倍频遍历算法获取叶片谐共振中心处的倍频值，但需安装传感器的数量较多。

本文通过比较GARIV法和扫频拟合法的优点，提出了新的同步振动参数辨识方法。该方法具体为先通过扫频拟合确定同步振动中谐共振点处的中心频率、幅值等参数；然后对存在的谐共振中心进行恒速运转，通过GARIV方法获得对应谐共振中心的倍频值，进而获得较为完整的叶片同步振动参数。在测试方案确定上，先将叶片对象模型化，通过对模型进行建模仿真来确定合适的传感器布置，安装角度的允许误差，测量时合适的运转转速值，以及多倍频存在时的辨识可行性等都做了验证，并针对模型给出了具体的要求。对于扫频拟合方法，通过仿真给出了合适的升速值，以及在数据处理过程中使用的拟合方法，以期提高拟合的准确性。最后通过一个仿真实例来综合展示新方法的辨识准确性。

1 叶片振动倍频值求解算法

1.1自回归算法(AR法)求解振动倍频值

Heath给出了自回归方法对同步振动下求解倍频值的具体推导过程。其中，假设叶片为单自由度无阻尼振动模型，且运转在谐共振中心频率处，通过推导可以获得使用4支等间距分布的传感器时，单叶片振动参数求解方程组为

(1)

式中:x1，x2，x3，x4分别为四支传感器监测到的叶片振动位移。a1=2cos(ωnΔtp);ωn表示叶片谐共振中心处振动角频率;Δtp表示叶片经过等间距传感器的时间间隔;DB为叶片振动的恒偏量。通过式(1)可以求解出a1和DB的值。

叶片同步振动过程中谐共振中心对应的倍频值可表示为

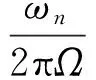
(2)

式中:n表示倍频值;Ω表示转频值。将a1=2cos(ωnΔtp)代入式(2)中可得：

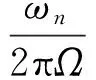
(3)

当传感器等间距分布之间的夹角为θ时(与下文中的传感器安装夹角相同)，则Δtp表示为

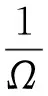
(4)

代入式(3)得：

(5)

推导中假设叶片组运转转速为谐共振中心处转速，但通过分析式(5)可知运转转速对振动倍频的求解没有影响。进而言之，只要a1值的求解准确，则在任何运转转速下都可以准确求解出振动倍频值。但考虑到实际情况中的误差、干扰及多倍频等的存在，需要对可运行转速做进行进一步的分析。

1.2GAR法及GARIV法

1.2.1 GAR方法

AR法是基于单叶片单圈数据进行分析的。考虑整机分析和测量分析的实时性，在AR的基础上进行扩展，提出GAR方法。通过对式(1)扩展得到GAR法的计算式为

(6)

式(6)中xR,B,p表示叶片B在第R圈时经过传感器p采集到的振动位移。上述公式仅仅在维度上进行了扩展，没有在实际测量过程中可能存在的干扰噪声等进行有效的处理。在GAR的基础上为了减弱噪声等干扰的影响，引入了辅助变量，即GARIV法。

1.2.2 GARIV方法

(7)

当测量过程中有误差时，记误差为εi，则有：

(8)

代入式(8)有：

(9)

上式可简写为如下形式：

Y=Xθ

(10)

引入辅助矩阵Z，该矩阵通过对矩阵X进行适当的平移后获得的，具体如下：

(11)

其中平移k值的选取为k=NAReq×R，式中NAReq为单圈单叶片可成立等式个数，如4个传感器时可成立的等式个数为2；5个传感器时，可成立的等式个数为3；R值的选取不定，k值往往选取可移动总数的10%。在实测数据处理中发现，平移k值对倍频值求取的影响较小。

对式(10)两边同时左乘ZT，则有：

ZTY=ZTXθ

(12)

由干扰的不相关性和假设测量误差的均值为0，可通过式(12)将包含误差εi的项消除，则测量误差对采用GARIV方法的影响较小，进而起到提高测量精度的要求，提高抗干扰能力。详细证明过程可参考文献[7]。

2 叶片振动倍频值测量方案

为保证辨识方法在实际测量使用时的可行性，需通过建模仿真对实际使用中可能出现的各种情况进行研究，最后给出有效可行的测量方案。

2.1仿真模型简介

为模拟实际情况下叶片振动，对实验台中使用的叶片模型化，见图1。建立质量-刚度-阻尼模型，不考虑叶片之间存在耦合，进而可对单个叶片做同步振动特性分析。

图1 从实际烟机叶片到实验台使用的简化叶片

2.2相关影响因素对AR法求取叶片振动倍频值的影响

2.2.1 单倍频时传感器安装夹角对倍频值求解的影响

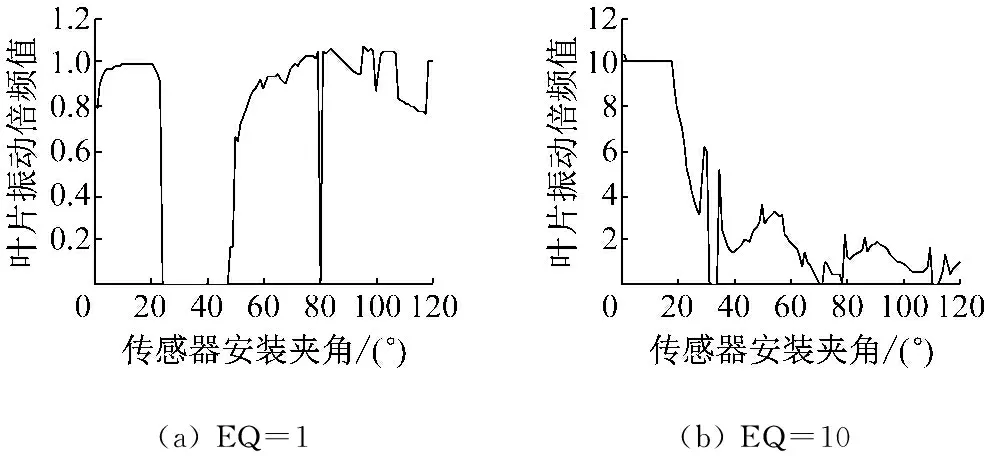
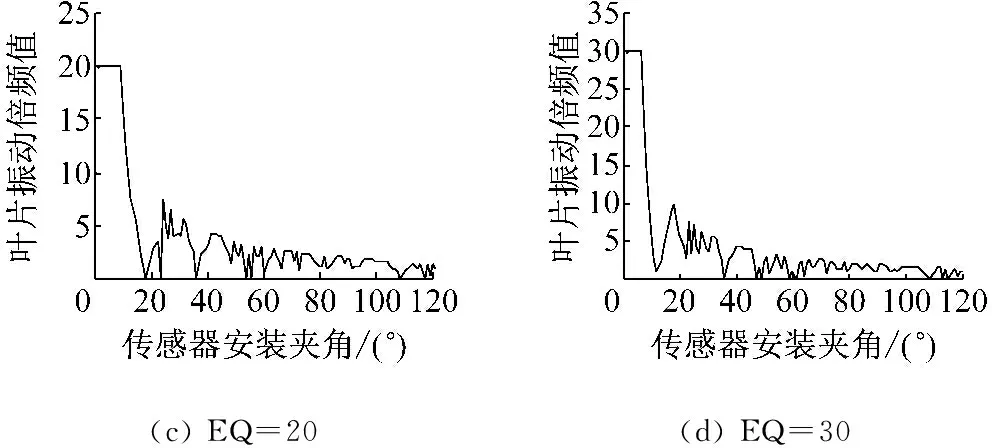
仿真中默认激振力仅激起单倍频下的叶片同步振动，传感器安装夹角变化范围为1°～120°，步长1°。仿真结果如图2所示，图(a)～(d)分别为1倍频，10倍频，20倍频和30倍频时，通过AR法求解的倍频值与传感器安装夹角之间的关系。

通过图2分析可知，随着倍频值的增大，为通过AR法获得准确的倍频值，则传感器允许的安装夹角在减小。例如分析1倍频时传感器允许安装夹角不超过20°，分析30倍频时传感器安装夹角不应超过6°。

(a)EQ=1(b)EQ=10

(c)EQ=20(d)EQ=30

图2 不同倍频下传感器安装夹角对倍频值求解的影响

Fig.2 The influence of the angle between sensors on solving the EO under different EO

通过仿真计算发现传感器1与键相传感器的初始夹角不会对AR法分析的结果产生影响。当使用AR法(GAR、GARIV法)时，传感器布置方面的要求为，根据叶片可能激起的倍频值确定合适的传感器布置夹角，这样才能通过AR法较为准确的获取叶片同步振动下的倍频值。

2.2.2 多倍频存在时AR法求解倍频值的准确性

在实际测量时，更多的是激起多倍频的情况，此时就需要研究AR法(GAR、GARIV法)能否很好的解决多倍频存在时的倍频值求取问题。

假设叶片模型中存在两个倍频值，分为两种情况。第一种为两个倍频值是依次关系，如19、20，对应的谐共振中心频率为78.95 Hz和75 Hz；第二种为两个倍频值相距较远，如11、20，对应的谐共振中心频率为136.36 Hz和75 Hz。激振力大小相同，同时传感器安装满足2.2.1中的要求。对两种情况下的两个谐共振中心频率附近进行恒速运转及倍频值分析。如19倍频时恒速运转转频范围为78.5～79.5 Hz，步长为0.1 Hz(下文中转频步长同样设为0.1 Hz)；20倍频处进行的恒速运转转频范围为74～76 Hz。每一运转转频通过AR法求得的倍频值，如图3所示。

11倍频处进行的恒速运转转频范围为135～138 Hz，11倍频和20倍频共存时不同运转转频下求取的倍频结果,如图4所示。

(1) 对上述两种情况的分析可知，多倍频存在时，通过AR法(适用AR的拓展法)可以分析出存在的叶片振动倍频值；

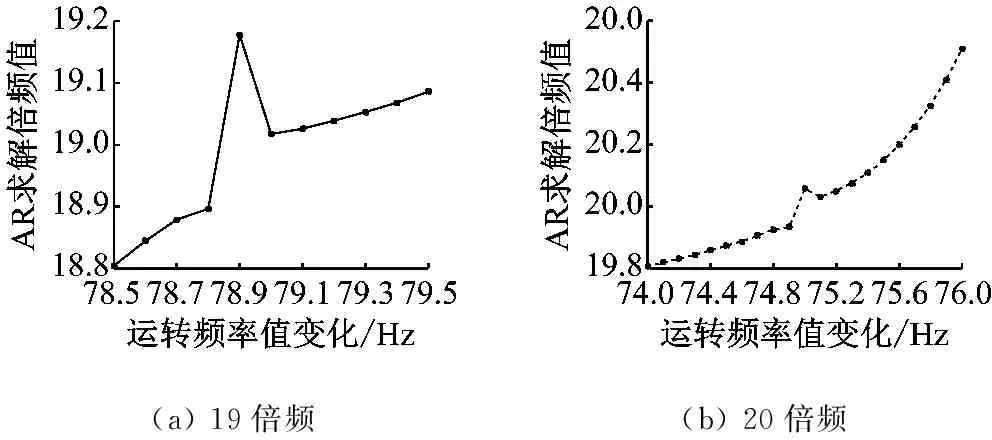
(a)19倍频(b)20倍频

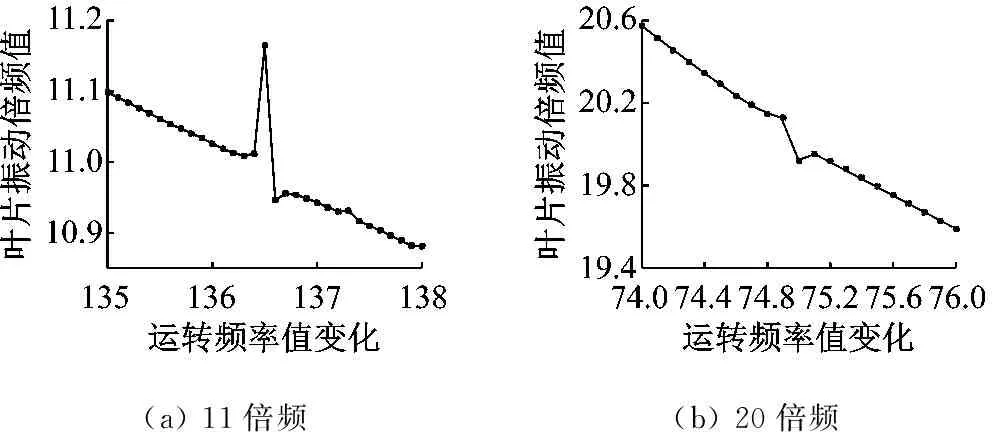
图3 倍频值为19和20时不同转频下求解的倍频值变化情况

图4 倍频值为11和20时不同转频下求解的倍频值变化情况

Fig.4 Obtained blade vibration EO at different operation speed for EO=11 and EO=20

(2) 在谐共振中心频率附近进行运转测量，对倍频值的求取也是非常准确的，即不需要将运转转频与谐共振中心频率保持一致，在谐共振中心频率附近也可以实现，这也与1.1节的结论对应。

2.2.3 测量过程中干扰(或噪声)对倍频值求取的影响

就实际测量系统而言，干扰或者噪声的存在是不可避免的。通过使用GARIV法可减弱噪声或干扰对测量结果的影响，提高测量精度。下面通过添加不同强度的高斯噪声来比较AR、GAR、GARIV三种方法在不同运转转频下的倍频值分析结果。假设模型存在多倍频19、20。添加噪声情况为：无噪声，信噪比为100，90，70四种情况。图5为倍频值20时不同噪声下三种分析方法在不同运转转频下的倍频值分析结果。

分析可知无噪声时，AR、GAR、GARIV三种方法获得的结果一样，如图5(a)。随着噪声的逐渐增大，GAR法计算的结果出现较大的偏差，AR法和GARIV法与正确值接近，但AR法在计算过程中会由于噪声的存在导致a1值超出允许范围而失效，综合比较可知GARIV法具有抗干扰能力，如图5(b)和(c)。随着噪声强度的增大，即SNR减小到70时，三种方法的测量结果都出现较大的误差，测量准确性降低，如图5(d)。总结而言，GARIV法对一定噪声下的测量分析结果较为准确，即具有较好的抗干扰能力，可用来分析实际测量中的振动倍频值。通过比较相同噪声，不同运转转频下的结果可知，越接近谐共振中心频率时，运转测量结果的准确性越高，抗干扰能力越强。所以，可以通过将运转转频接近谐共振中心频率来提高倍频值的测量精度，但也需要考虑到谐共振中心处的叶片振动局部最大，避免发生危险情况。

(a)无噪声,不同运转转频下倍频值求解(b)SNR=100,不同运转转频下倍频值求解

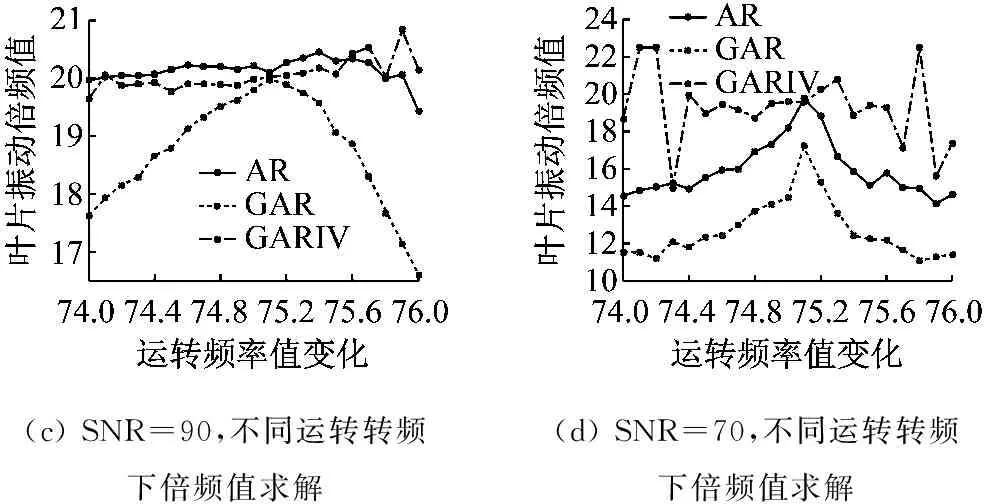
(c)SNR=90,不同运转转频下倍频值求解(d)SNR=70,不同运转转频下倍频值求解

图5 20倍频，不同信噪比和运转转频下倍频值求解

Fig.5 Comparison of the results of blade vibration EO at different rotating speed and noise

2.2.4 传感器安装角度误差对倍频值求取的影响

针对安装角度误差，通过按一定范围内生成随机数，以达到产生随机夹角误差的目的。为避免特殊情况的发生，通过大量随机产生的模拟误差来研究安装误差对倍频值求取的整体影响趋势。

同时由于分析公式中对传感器安装夹角有要求，仿真中分别通过设计夹角和平均夹角两种情况来对比哪种夹角下的分析结果更准确。平均夹角由各传感器的夹角经实际测量并平均后获得。图6为倍频值20，添加噪声一定时，不同最大夹角误差时的仿真结果对比。考虑到实际运转转频不可能与谐共振中心频率相同，故选取运转转频为75.2 Hz。

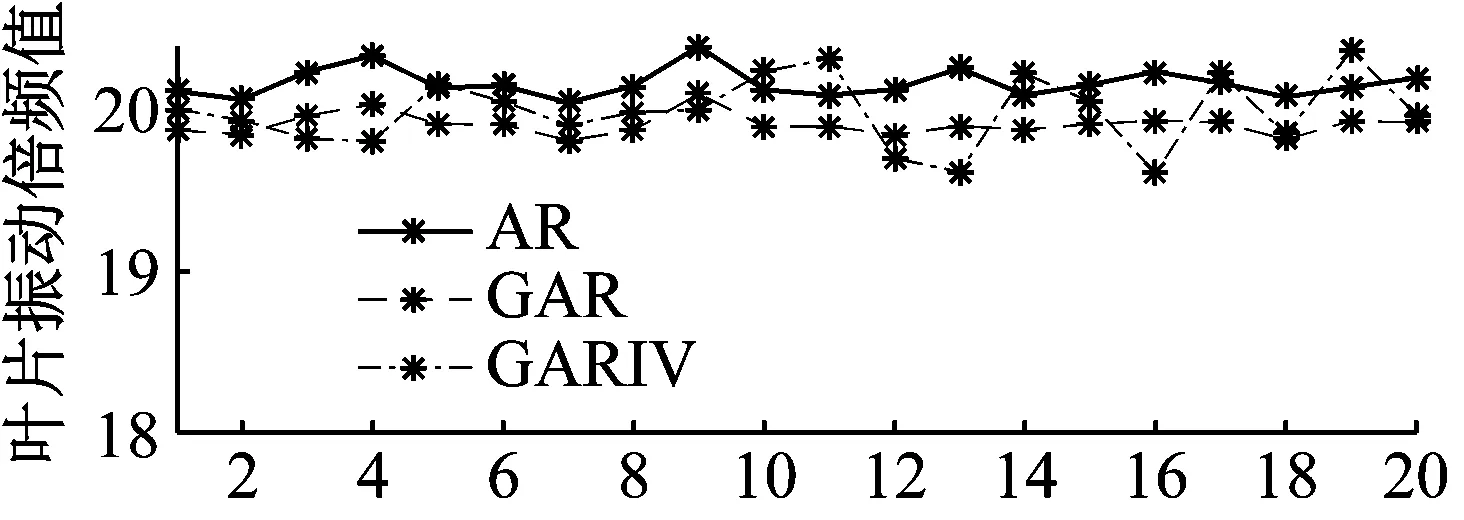
(a) 夹角误差最大0.5°，平均夹角下运行次数

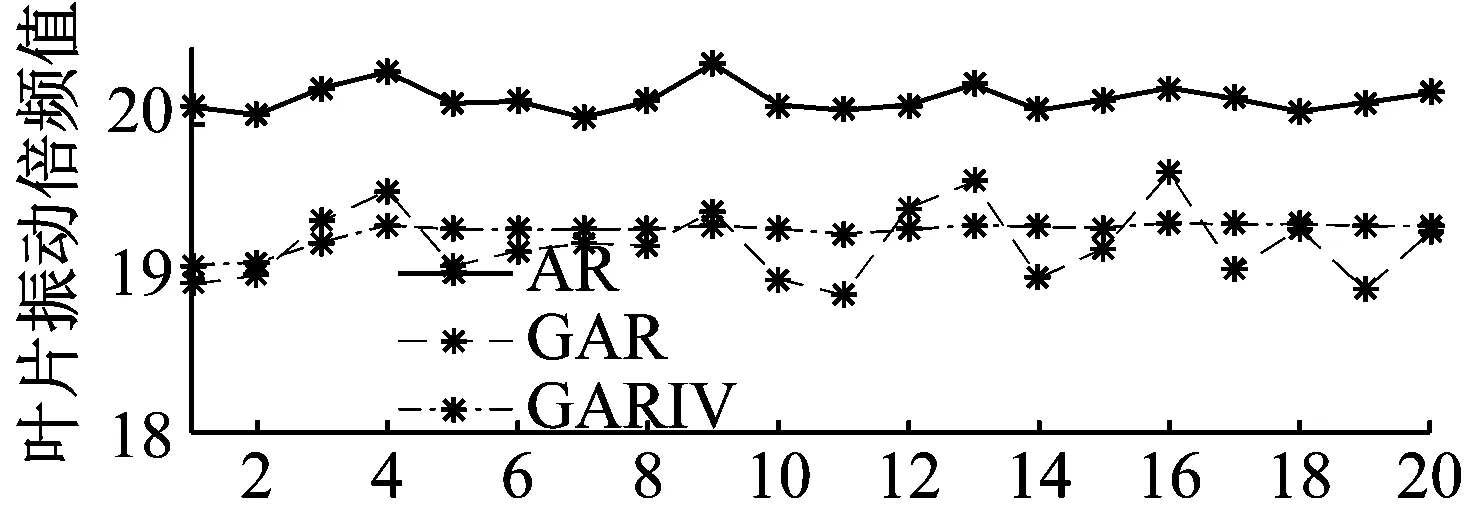
(b) 夹角误差最大0.5°，设计夹角下运行次数

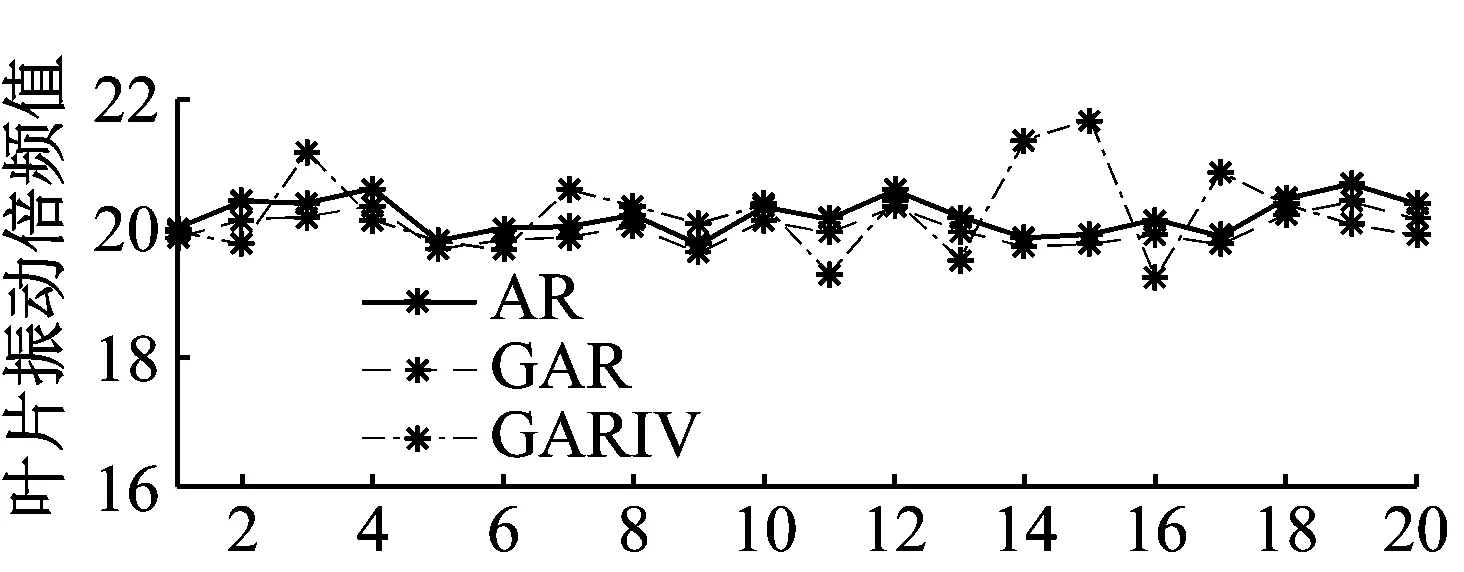
(c) 夹角误差最大1.5°，平均夹角下运行次数

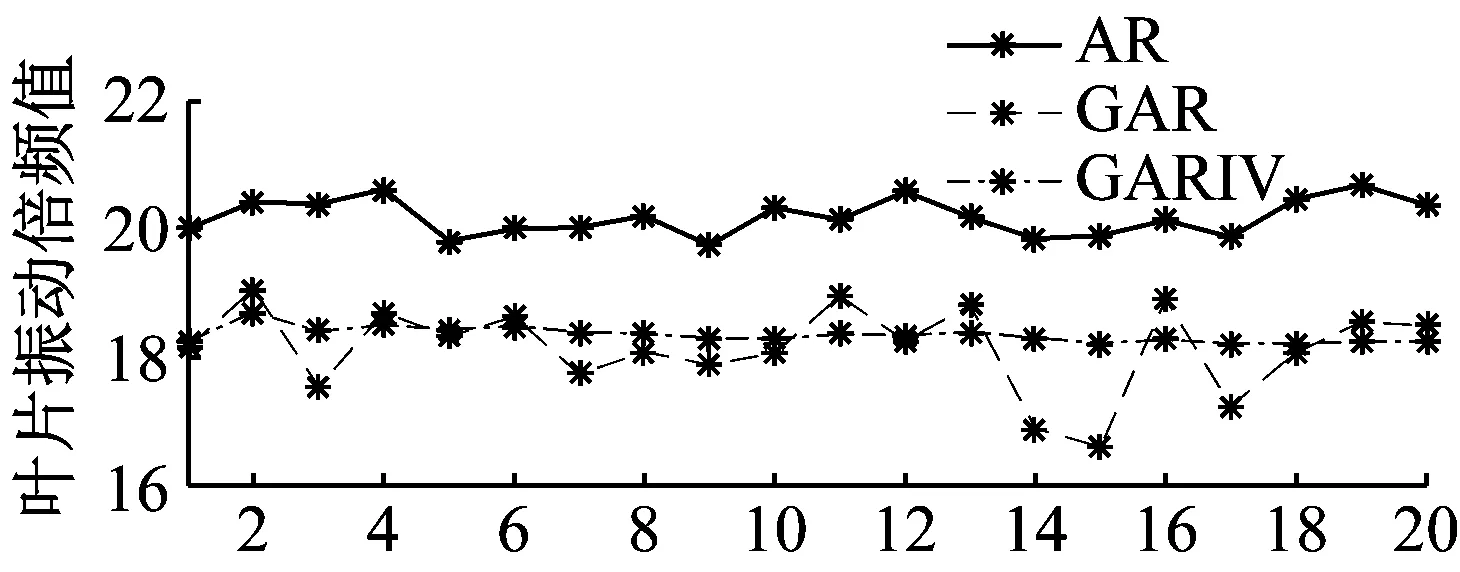
(d) 夹角误差最大1.5°，设计夹角下运行次数

通过图6分析可知，相同噪声下，采用平均夹角的计算结果要比采用设计夹角的计算结果更准确。同时随着夹角误差的增大，采用设计夹角的分析结果虽然较为平稳，但与正确值偏差增大。采用平均夹角的分析结果虽然与准确值接近，但也出现了较大的波动。

总结以上，在设计和安装传感器时，不能超出允许夹角的同时，可通过动态测量的方式获得各传感器之间的夹角，进而获得平均安装夹角。应保证各安装夹角相等，且与设计值保持一致。

3 扫频拟合分析与坎贝尔图的获取

3.1扫频拟合分析

将旋转叶片简化成悬臂梁，不考虑叶片之间耦合时，叶片振动位移随转频之间的响应函数可表示为

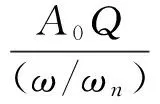
(13)

式中:A0为激振力幅值；Q为品质因数，Q=1/(2ξ);ξ表示阻尼比；A0Q表示振动幅值；ω为转频；ωn为中心转速频率；φ表示初始相位；DC为叶片振动恒偏量。η′表示如下：

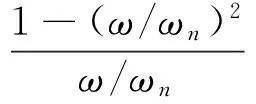
(14)

当叶片运转转速经过谐共振中心转频时，叶片在激振力的作用下会产生较大的振动。根据振动位移与转频之间的响应函数，可通过非线性最小二乘拟合算法获得谐共振中心频率、振动幅值、初始相位、振动恒偏量等参数。非线性最小二乘拟合算法具体内容可参考LM法[9-10]。

在仿真实验过程中发现，不同升速情况下，叶片振动相应曲线不同，如图7所示。

图7 不同升速情况下叶片振动位移响应曲线

响应曲线是拟合的数据源，对拟合结果影响很大，所以需通过仿真对升速值进行确定。可有效保证实际测量时叶片振动参数拟合的准确性。在上述仿真的基础上，通过不同升速下的拟合结果来确定可允许的最大升速值。

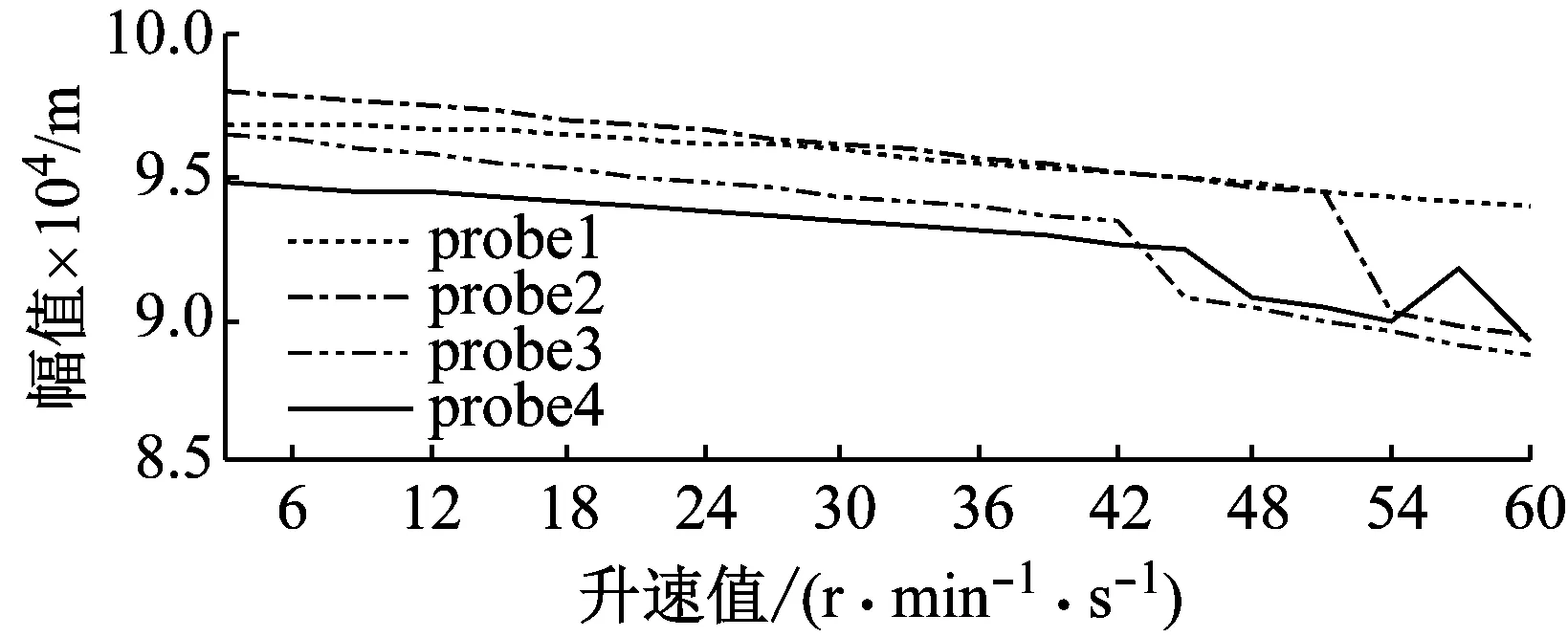
图8 不同传感器在不同升速下的响应曲线拟合情况

通过图8可知，在不同升速下叶片振动幅值的拟合结果不同，随着角加速度的增大，拟合获得的幅值逐渐减小，与实际值偏离逐渐增大，拟合的误差逐渐增大，所以选择合适的升速值可通过拟合获得较为准确的叶片同步振动参数。

3.2综合验证

为综合验证扫频拟合结合GARIV法来辨识叶片同步振动参数，进而获得叶片振动坎贝尔图。建立的仿真模型参数设置与2.1节一致，叶片运转区间内被激起的倍频值和振幅对应关系,如表1所示。

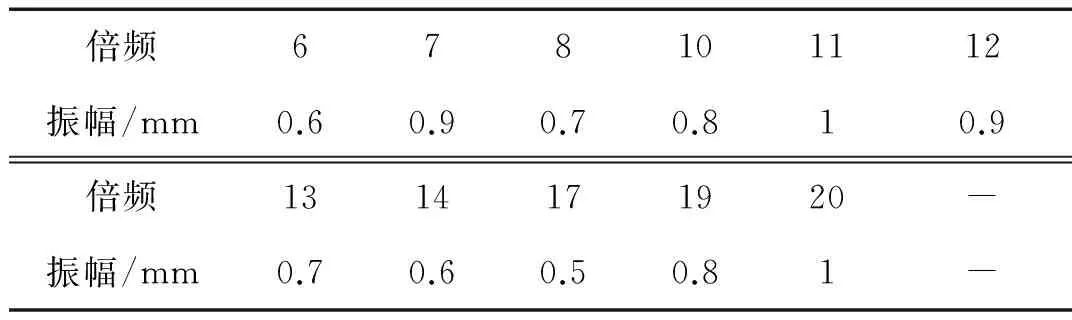
表1 模型参数设置

仿真时传感器布置角度满足前文中的要求，在振动位移的结果上添加10%的高斯白噪声。

先通过扫频运转获得叶片振动位移随运转转速的变化情况，初步识别出存在的谐共振区间和粗糙的共振中心频率，然后对提取出的谐共振区间进行非线性最小二乘拟合(LM法拟合)获得叶片振动位移响应曲线的参数，包括谐共振中心频率、振动幅值、相位、振动恒偏量等。对四支传感器拟合的结果进行平均获得叶片同步振动参数。根据扫频结果针对存在的每一个谐共振区间选取合适的运行转频，然后进行恒速运转仿真，四支叶顶传感器监测到的振动位移经过GARIV方法分析可以获得叶片各个谐共振中心对应的振动倍频值。表2为通过扫频拟合获得的谐共振中心频率和振动幅值，以及GARIV分析获得的振动倍频值(表中的频率指谐共振中心频率)。

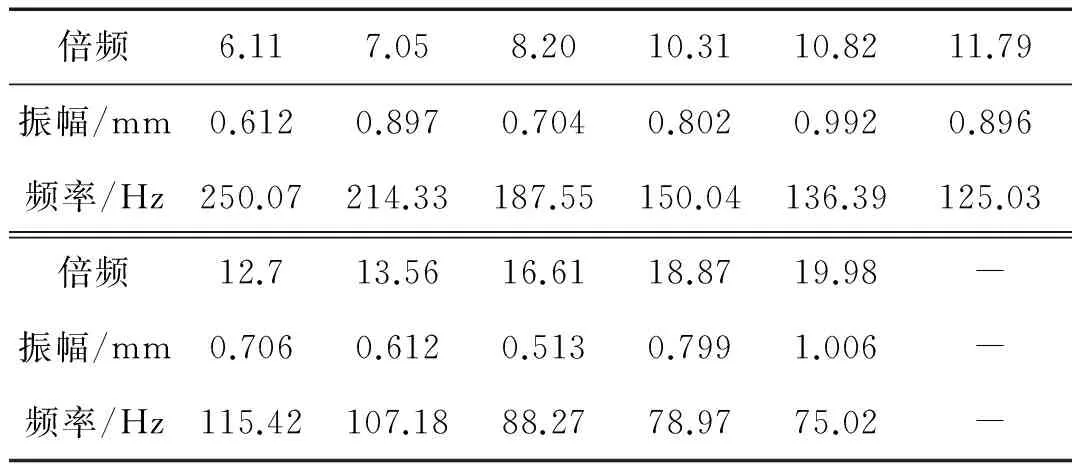
表2 叶片振动参数辨识结果

通过上表可以发现LM法对叶片振动幅值和谐共振中心的拟合结果是非常准确的，GARIV方法也较准确的分析出各谐共振中心对应的振动倍频值。通过上表可以获得叶片振动坎贝尔图，如图9所示。

图9 叶片振动坎贝尔图

4 结 论

本文提出了扫频拟合分析和GARIV法相结合来辨识叶片同步振动时的振动参数。主要完成以下：

(1) 通过建模仿真给出了不同倍频下传感器允许的安装夹角，验证了AR法及其扩展法可对单倍频和多倍频进行有效辨识，同时也对运转转速的选择做了说明。

(2) 验证了GARIV法对叶片振动倍频识别的准确性，以及抗干扰能力；通过仿真对传感器安装夹角的误差进行了规范，提出GARIV分析算法中计算采用传感器平均夹角。

(3) 在使用扫频拟合方法的过程中，通过比较不同升速值下的叶片振动参数拟合结果提出了合适的升速值。

通过结合两种方法的优点可辨识出叶片同步振动参数，在准确辨识的基础上将使用的传感器数量减少到四个，可较好的满足工程应用。

[1] PICKERING T M. Methods for validation of a turbomachinery rotor blade tip timing system[D]. Blacksburg: Blacksburg Virginia Tech University, 2014.

[2] ABDELRHMAN A M, HEE L M, LEONG M S, et al. Condition monitoring of blade in turbomachinery: A review[J]. Advances in Mechanical Engineering, 2014(2014)：210717.

[3] DIMITRIADIS G, CARRINGTON I B, WRIGHT J R, et al. Blade-tip timing measurement of synchronous vibrations of rotating bladed assemblies[J]. Mechanical Systems & Signal Processing, 2002, 16(4): 599-622.

[4] HEATH S. A new technique for identifying synchronous resonances using tip-timing[J]. Journal of Engineering for Gas Turbines and Power, 2000, 122: 219-225.

[5] 欧阳涛. 基于叶尖定时的旋转叶片振动检测及参数辨识技术[D]. 天津: 天津大学, 2011.

[6] ROBINSON W, WASHBURN R. A real time non-interference stress measurement system (NSMS) for determining aero engine blade stresses[C]//Proceedings of the 37th Symposium of the Instrumentation Society of America, San Diego, California. 1991: 91-103.

[7] CARRINGTON I B. Development of blade tip timing data analysis techniques[D]. Manchester: University of Manchester, 2002.

[8] 欧阳涛, 郭文力, 段发阶, 等. 基于叶尖定时的旋转叶片同步振动辨识新方法[J]. 振动与冲击, 2011, 30(8): 249-252.

OUYANG Tao, GUO Wenli, DUAN Fajie, et al. New method for identifying rotating blades synchronous vibration based on tip-timing[J]. Journal of Vibration and Shock, 2011, 30(8): 249-252.

[9] FREUND O, MONTGOMERY M, MITTELBACH M, et al. Non-contact test set-up for aeroelasticity in a rotating turbomachine combining a novel acoustic excitation system with tip-timing[J]. Measurement Science and Technology, 2014, 25(3): 116-121.

[10] 张光澄. 非线性最优化计算方法[M]. 北京: 高等教育出版社， 2005： 159-169.

Synchronousvibrationparametricidentificationmethodforbladesofaturbine

WANG Weimin, REN Sanqun, CHEN Lifang, HUANG Shan

(Beijing Key Laboratory of Health Monitoring Control and Fault Self-recovery for High-end Machinery, Beijing University of Chemical Technology, Beijing 100029, China)

A new method used to identify a turbine’s blade synchronous vibration parameters based on the blade tip-timing (BTT) non-contact type blade vibration measurement technique and previous studies in this field was proposed here. According to the measured relationship between blade vibration displacement and rotating speed, the parameters, such as, the center frequency of blade’s harmonic resonance points, the maximum amplitude of blade vibration, and its initial phase were computed with the nonlinear least square fitting algorithm. If the blade assembly was operated at a constant rotating speed being close to the frequency of its resonance point, different blade vibration displacements were measured with sensors at different positions. The double-frequency vibration displacements of various blades at their corresponding harmonic resonance points were computed with the global autoregressive with instrumental variables (GARIV) method. A blade’s Campbell diagram was made with its vibration parameters obtained using GARIV method and the sweep frequency fitting method. Based on this method, the locating scheme of BTT sensors was proposed, interference factors existing in the actual measurements were analyzed in detail, the feasibility of the proposed method was verified. The test verification of this method will be published later.

turbine blades; synchronous vibration; parametric identification; blade tip-timing (BTT); GARIV method

国家自然科学基金(51275028; 51135001)

2016-11-01 修改稿收到日期：2016-12-16

王维民 男，博士，教授，1978年4月生

陈立芳 女，博士，讲师，1973年3月生

TK14； V216.2

： A

10.13465/j.cnki.jvs.2017.17.019