运行状态下海上风机结构振源特性研究

董霄峰， 练继建， 王海军

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2. 天津大学 前沿技术研究院有限公司，天津 301700)

运行状态下海上风机结构振源特性研究

董霄峰1,2， 练继建1,2， 王海军1,2

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2. 天津大学 前沿技术研究院有限公司，天津 301700)

由于海上风机结构运行环境的复杂性，其振源的准确识别与振源特性研究已经成为风机运行安全性评估的重点问题。以某新型复合式筒型基础结构海上风力发电试验样机为研究对象，依据原型观测获得的全负荷条件下结构不同位置的振动响应数据，对不同运行工况下诱发结构振动的振源进行全面识别与分析。利用谱峭度法识别明确引起海上风机结构振动的主要振源及其对应振动响应的频域属性，通过经验模态分解法对实测信号进行分解得到表征各振源特性的频域或频率尺度的分量，同时引入振动能量法对不同振源的能量比重进行统计分析，给出了海上风机结构运行状态下结构整体振动主振源及其对应振动能量分布随运行因素变化的分布规律。研究表明随着机组负荷的增加运行状态下海上风机结构振动的振源变化遵循由单一的环境荷载激励转为环境荷载激励和叶轮转动联合作用再到完全由叶轮转动产生的谐波激励影响的规律。

海上风电；现场实测；振源识别；谱峭度；经验模态分解；振动能量

海上风机结构在运行状态下往往受到风、浪、流等复杂多变环境荷载的联合作用，由于风机机组与支撑结构连为一体，结构振动主要为机组与支撑结构的耦联振动，响应信号中既体现机组运行的特点同时也包含环境激励下结构自身的振动特性。机组运行为支撑结构提供振源，支撑结构振动又反作用于机组，风机结构过大的振动不仅对自身产生破坏作用，还对机组结构的稳定性造成影响。有鉴于此，近年来有关海上风机结构运行状态下安全状况方面的研究越来越受到人们的重视，并成为当前风电领域的热点研究问题之一。

目前、国内外对风机结构运行状态下的振动特性与结构安全性研究还多停留在通过模拟环境荷载和结构计算来实现[1-3]，重点关心外界荷载对于结构的作用效力而忽略了结构内部运行环境的影响。另外，基于现场原型观测的结构振动资料主要还仅限于结构动态参数的识别[4-5]，而对海上风机结构振动的诱因和结构振动能量分布特性的研究凤毛麟角。因此，为探究海上风机结构振动的振源特性并准确把握各种振源能量的分布变化规律，本文以某海上风力发电机实测振动响应为研究依据，首先基于谱峭度法(Spectral Kurtosis)获取结构振动的主要振源类型与对应振动频率的振动属性，此后采用经验模态分解法(EMD)对信号按频域由高到低进行分解排列，将各阶信号频分与可能的激振源频率进行比对并完成对结构在工作状态下振源的初步识别，再引入振动能量法对与通频内各信号分量所对应的不同振源能量所占振动总能量的比重进行统计分析，最后归纳海上风机结构运行状态下结构整体振动主振源及其对应振动能量分布随运行因素变化规律，为海上风机结构运行安全性评估工作提供必要的理论依据。

1 基本理论与方法背景

1.1谱峭度法

对于实测离散随机信号X(t)，其离散傅里叶变换为X(f)，则信号X(t)的谱峭度可以定义为复随机变量X(f)在每个频分f处的峭度[6]，按照如下形式表示：

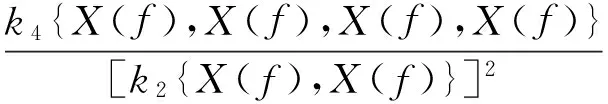
(1)

式中：X(f)∈{X(f),X*(f)}；X*(f)是X(f)的复共轭形式；kr是第r阶累积量。若X(t)为一平稳随机过程，则频域X(f)成分可以表达为每个频率f处循环的复随机变量，这就说明对于X(f)的非零累积量其共轭成分与非共轭成分要保持一致，则式(1)又可以写为

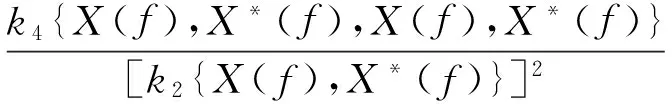
(2)

根据复随机变量的循环性，每种频率成分处的峭度值以期望的形式定义为：

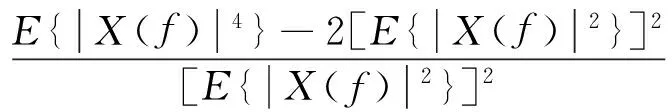
(3)

在实际应用中，对于数据长度为L的信号X(t)，通常在时域上需预先确定数据长度为N的时间窗口，保证信号X(t)可以分割为M个非重合的信号区域，并且恒有M×N=L。对首个信号区域内信息进行独立的N点离散傅里叶变换为XN(f)，随后沿时间轴移动窗口，即可以得到不同时段的频谱，对不同频带内的傅里叶谱统计其相应的峭度，就能够绘制出整体的谱峭度。以上操作后，离散信号X(t)的全频域内的谱峭度的无偏估计值可以写为

(4)

谱峭度法最重要的用途之一是检验信号中不同频分振动的属性，即判断信号成分是体现随机振动特性还是受迫振动特性[7]。然而，保证谱峭度法精度的主要影响因素是对信号分段数M的选取，M选取不当容易造成谱峭度整体计算的失真。因此，为避免信号数据长度与区块划分对传统谱峭度计算精度的影响，文献[8]提出了一种行之有效的求解谱峭度的过程，其思路是根据对实测数据分析的需要，预先划定适宜宽度的频带将整个频域分割为若干的单位频段，通常采用窄带带通滤波的方法，再基于峭度的基本定义对每个频段内的振动响应求解其峭度值，将获得的峭度值在全频域进行分布即得到谱峭度。此种区分振动随机特性与谐波特性方法的判断标准较为简单，即当某种频域或频率内的响应为随机特性激励诱发所致的，其峭度值通常稳定在3.0附近，而当振动响应体现谐波受迫特性时，其峭度值一般接近于1.5。

1.2振动能量理论

假设同样的实测离散随机信号X(t)含有多种频分，其内部各频分信号均为零均值平稳随机过程，则X(t)表达式可以写为各信号累加之和：

(5)

式中：i为信号中包含频分的个数(i=1，2，…，n)；Ci(t)为信号X(t)中不同频分信号表达式，每一个Ci(t)理论上对应一个频率或一段频域。

原始信号经过EMD法分解会得到数量若干的标准IMF分量[9-10]，各IMF分量按照频域由高到低排列的顺序分别表征原始信号中所包含的不同频分尺度的信号成分，理论上可以与Ci(t)相互对应，其数量为n。为了说明信号的能量分布特征，在此引入振动信号能量法理论，对于原始信号X(t)其总振动能量可以表示为信号幅值平方对时间的积分[11-12]：

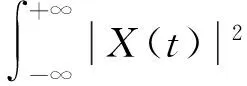
(6)

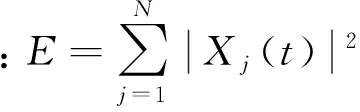
(7)

式中：j为信号X(t)的离散数据个数(j=1，2，…，m)；E为原始信号总能量；Xj(t)为对应信号中的单个数据。同样对于原始信号每一阶分解后的分量Ci(t)，其具有的振动能量Ei可以按如下表达式计算得到：

(8)

由于信号分解后的IMF分量具有正交性，因此各阶分量信号能量与原始信号总能量应存在如下恒等关系[13]：

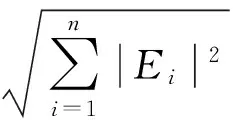
(9)

定义信号各阶分量能量比重为Wi，其可以说明原始信号在不同频域内的能量分布特性，具体表达式可以写为

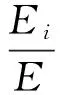
(10)

1.3振源与能量分布识别流程

基于以上介绍的谱峭度法与振源能量理论，考虑实际海上风机结构在运行状态下的激励特性，可以确定结构振源及其能量分布特性识别流程如下：

(1) 选取风机典型运行工况，通过频域分析与谱峭度法确定海上风机结构实测振动的主要频域特性与主振源的属性；

(2) 对原始信号进行EMD分解，将分解各阶信号主频与风机可能振源激励频率进行比较，确定振动中存在主要振源类型与特性；

(3) 基于振动能量理论对EMD分解后各阶信号进行能量计算，确定各类振源在振动信号中所占有的能量比重。

以上识别流程可将谱峭度法、EMD信号分解法与振动能量理论较好地结合起来，从而实现海上风机结构振源及其能量分布的同步识别。

2 工程概况

测试海上风机采用直驱式机组形式，额定功率2.5 MW，额定转速18 r/min，风机基础采用复合式筒型基础形式[14-15]。风机叶轮直径93.4 m，轮毂高度80.0 m，塔筒为三段式安装，机舱与塔筒及相邻塔筒之间设有工作平台。基础总高25.2 m，下部筒体高度7.2 m，上部筒身高度18 m，下部筒体底面直径30 m，基础总重量约为2 500 t。测试在塔筒内部由上至下布置5个测点，位置为距离工作平台高度约1.5 m处的塔筒壁上，具体布置位置参见图1所示。传感器选择低频振动位移传感器，频响范围最低可达到0.1 Hz，均为三向测振，满足采集结构低频多向振动信号的试验目的。

图1 现场测点布置示意图

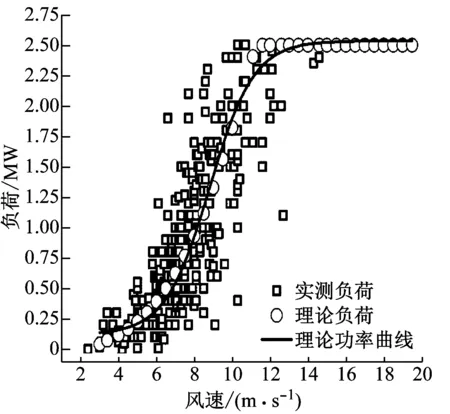
图2 现场实测负荷与理论负荷比对图

图2显示随风速变化现场实测机组负荷分布趋势与理论机组负荷分布基本保持一致，且满足风机机组理论功率曲线，从而说明实测获得机组负荷数据与实测结构振动响应数据真实可靠。而同时为清楚地说明海上风机结构在运行过程中振源及其能量分布的变化规律，本文选取多组现场测试工况并将整个风机运行机组负荷范围分成三个区域，分别按照低负荷区(0～800 kW)、中负荷区(800 kW～1 700 kW)及高负荷区(1 700 kW～2 500 kW)进行研究说明。

3 方法工程应用与验证

选择两组典型运行工况来说明提出方法的工程适用性，工况1参数：运行风速4.0 m/s、叶轮转速8 r/min、机组负荷150 kW；工况2参数：运行风速10.7 m/s、叶轮转速18 r/min，机组负荷2 500 kW，图3和图4分别给出两种运行条件下风机振动信号的功率谱与谱峭度图。

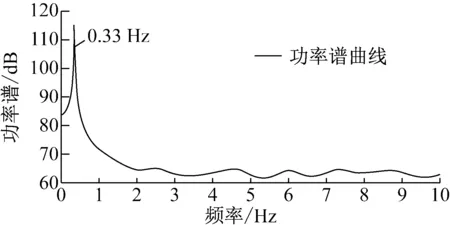
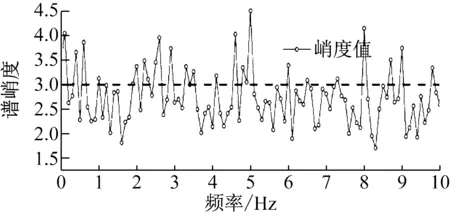
图3 工况1时响应信号功率谱密度与谱峭度

从图3可以看出，工况1结构振动主要频率集中在0.33 Hz处，其对应的峭度值在3.0附近，说明此时风机振动主要体现结构随机振动特性。其原因可以归结为在风机运行参数较低的情况下，结构振动主要受到环境荷载的作用，其激励结构以其自身的结构固有模态频率进行振动，风机运行引起的谐波激励对结构产生的作用较小。

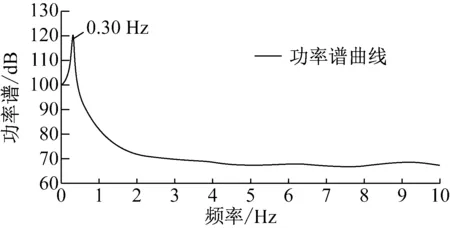
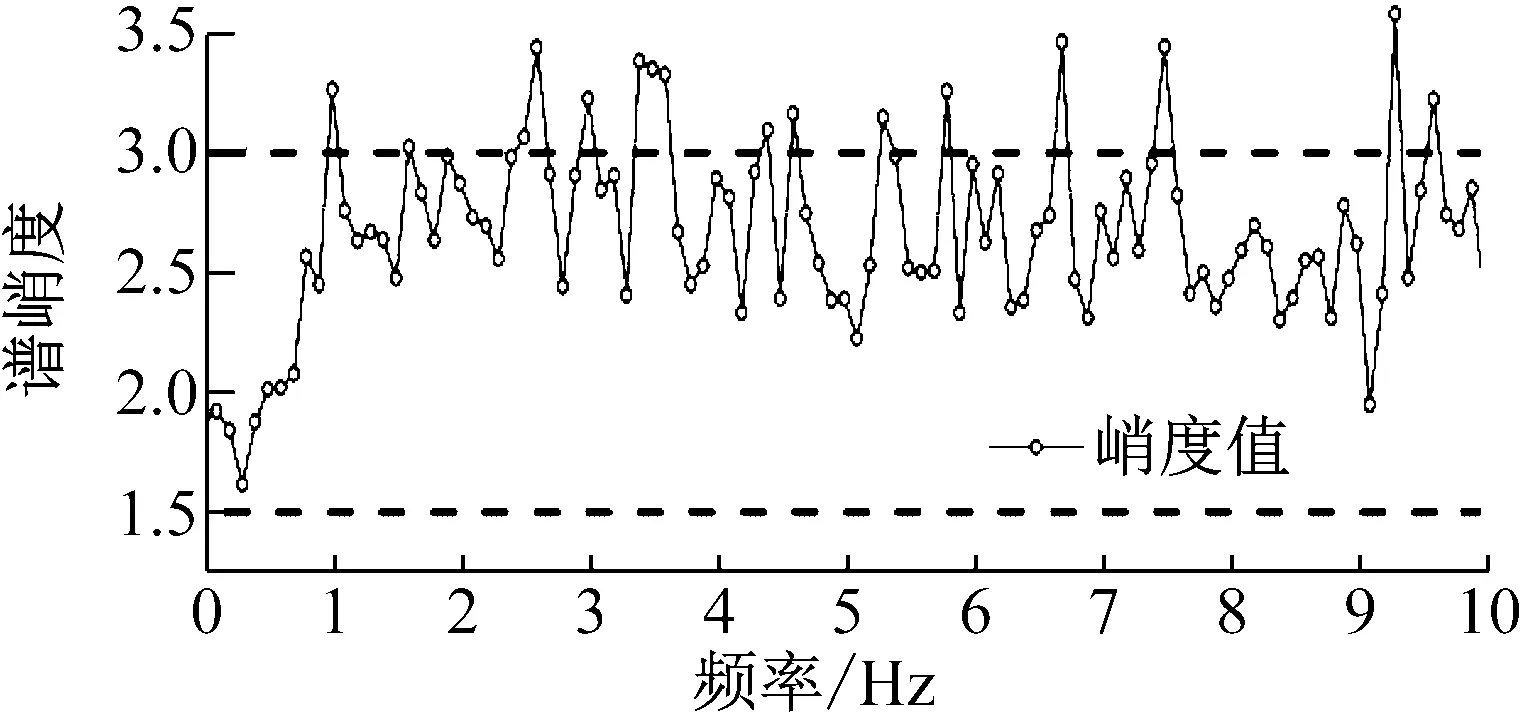
图4 工况2时响应信号功率谱密度与谱峭度

图4中可以看出，此工况下风机结构振动的优势频率仅稳定在0.30 Hz附近，这与叶轮转频保持一致，说明此工况下风机结构振动主要受到叶轮转动的影响。再对应到相应的谱峭度图中，0.30 Hz频率处存在明显的向下的峰值，数值上接近于1.50，这说明响应中0.30 Hz频率对应的振动体现较为稳定谐波特征。

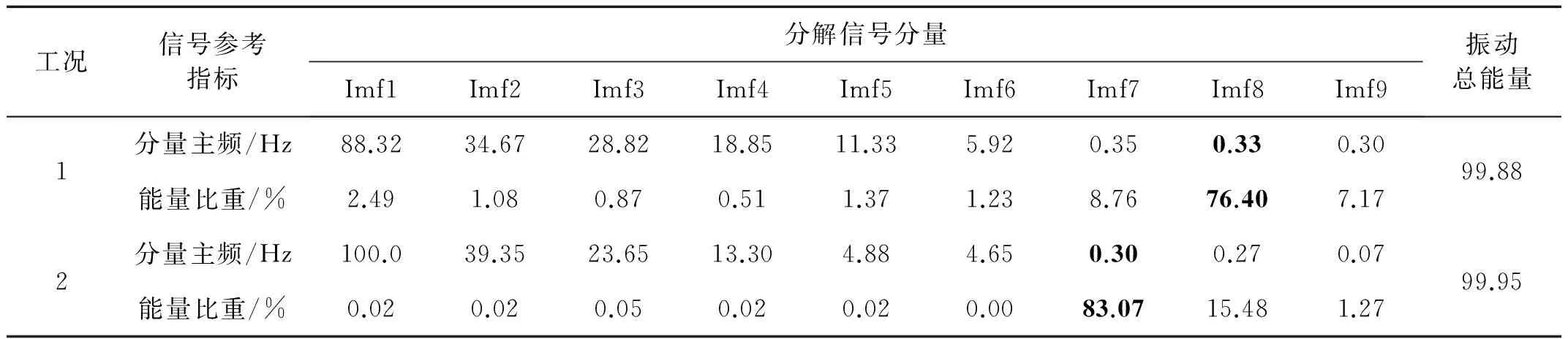
表1 典型工况分解各阶分量信号主频与能量比重统计表

表2引起风机结构振动的振源类型和频率信息表

Tab.2Vibrationsourcetypesandcorrespondingfrequenciesofwindturbinestructure

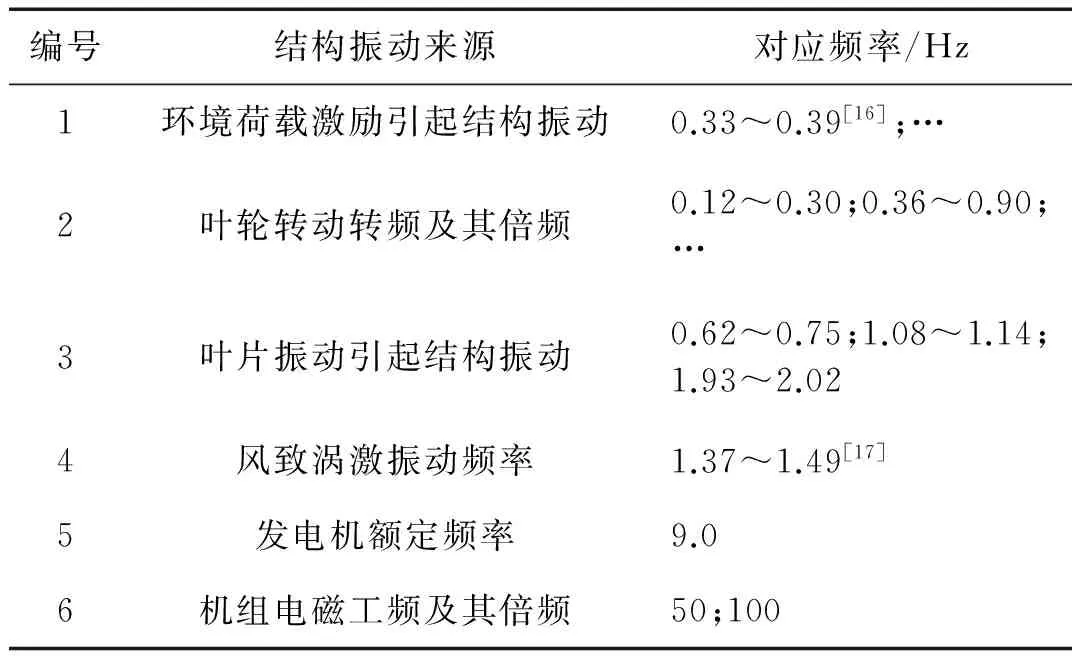
编号结构振动来源对应频率/Hz1环境荷载激励引起结构振动0.33～0.39[16];…2叶轮转动转频及其倍频0.12～0.30;0.36～0.90;…3叶片振动引起结构振动0.62～0.75;1.08～1.14;1.93～2.024风致涡激振动频率1.37～1.49[17]5发电机额定频率9.06机组电磁工频及其倍频50;100

表1给出了基于EMD法对两种工况信号分解后获得各阶分量主频与能量比重信息，可以知道各阶分量信号能量比重总和基本维持为100%，结构振动能量主要集中在信号前9阶分量且足够可以表征原始信号的全部主要频域特性。而表2为根据风机结构的受力、工作特点同时参考风力发电机组的振源理论给出的可能引起海上风机结构振动的振源类型与对应频率。具体由表1可知，海上风机结构在工况1时主要能量分布在主频为0.33 Hz的第8阶分量上，能量比重76.40%，而工况2时结构振动能量则主要集中在优势频率为0.30 Hz的第7阶信号分量上，能量比重83.07%。与表2中可能振源激励频率进行比对可知，两种工况下海上风机结构振动的主振源分别为环境荷载激励与机组运行引起谐波激励。

4 海上风机结构振源识别

基于本文提出方法对不同负荷工况实测数据进行分析，获得对应的主要振源频率分布情况见图4所示。与表2中的理论振源频率进行对照可知，0.16～0.30 Hz范围内频率为不同工况下机组转频，0.41～0.60、0.78～0.93、1.00～1.27、1.66～1.81、2.05～2.49、2.62～2.70 Hz等频域范围为风机运行多倍转频；0.33～0.37 Hz、1.32～1.35 Hz、2.51～2.57 Hz频率范围则对应风机结构自身的前三阶模态频率，0.62～0.75 Hz、1.08～1.14 Hz、1.93～2.02 Hz范围内频率应为风机叶片的前三阶固有频率，这三种振源频率的响应均为结构受环境荷载激励后所产生；另外在1.37～1.49 Hz范围内出现次数较少的频率可能为较高风速条件下风致涡激振动的频率。

图5 海上风机结构主要振源频率分布图

5 振源及其能量随运行因素变化规律

5.1运行因素对结构主振源的影响规律

图6给出了海上风机结构在不同负荷范围内，各测点振动位移信号主频率出现次数统计分布趋势示意图，图中实心点表示经谱峭度分析后该频率为谐波成分，而空心点则是代表结构模态成分的振动频率。由图可知，海上风机结构在机组负荷较低工况下，结构主振频率范围为结构低阶模态频率0.33～0.35 Hz，体现结构受环境激励而产生固有模态特性。该工况下风机机组运行较为缓慢，仅对塔筒上部存在微弱影响，如图6(a)中1#测点在0.21 Hz附近出现的频率分布峰值。随着负荷的增加，逐渐增大的运行转速对结构的影响程度开始上升，集中体现在图6(b)中0.25～0.26 Hz频域内各测点均出现了明显的主频分布峰值。但由于受到机组负荷的限制，机组运行并没有成为结构振动的唯一振源，环境激励下结构振动在振源成分中仍占有较大的比重，振动主频分布峰值存在于0.33～0.34 Hz范围内，说明此时结构振动是由风机运行与环境荷载联合激励下发生的。当机组负荷增加至接近额定功率时，机组运行对结构的影响也达到最大，结构振动主频的分布峰值仅于额定转频0.30 Hz附近出现，而体现结构一阶模态的0.33 Hz出现次数明显减少。说明在高负荷条件下风机振动的主振源来自机组运行过程中的叶轮转动，环境激励影响较小。

综上可知，随着机组负荷的增加海上风机结构振动的主振源变化遵循由单一的环境激励转为环境荷载和叶轮转动联合作用再到完全由叶轮转动引起谐波激励影响的规律。结构振动形式从低负荷条件下按固有模态频率振动，转变为中等负荷下环境荷载与风机运行引起谐波激励作用下的联合振动，再到高负荷下完全由机组运行影响下的纯受迫振动的变化过程。

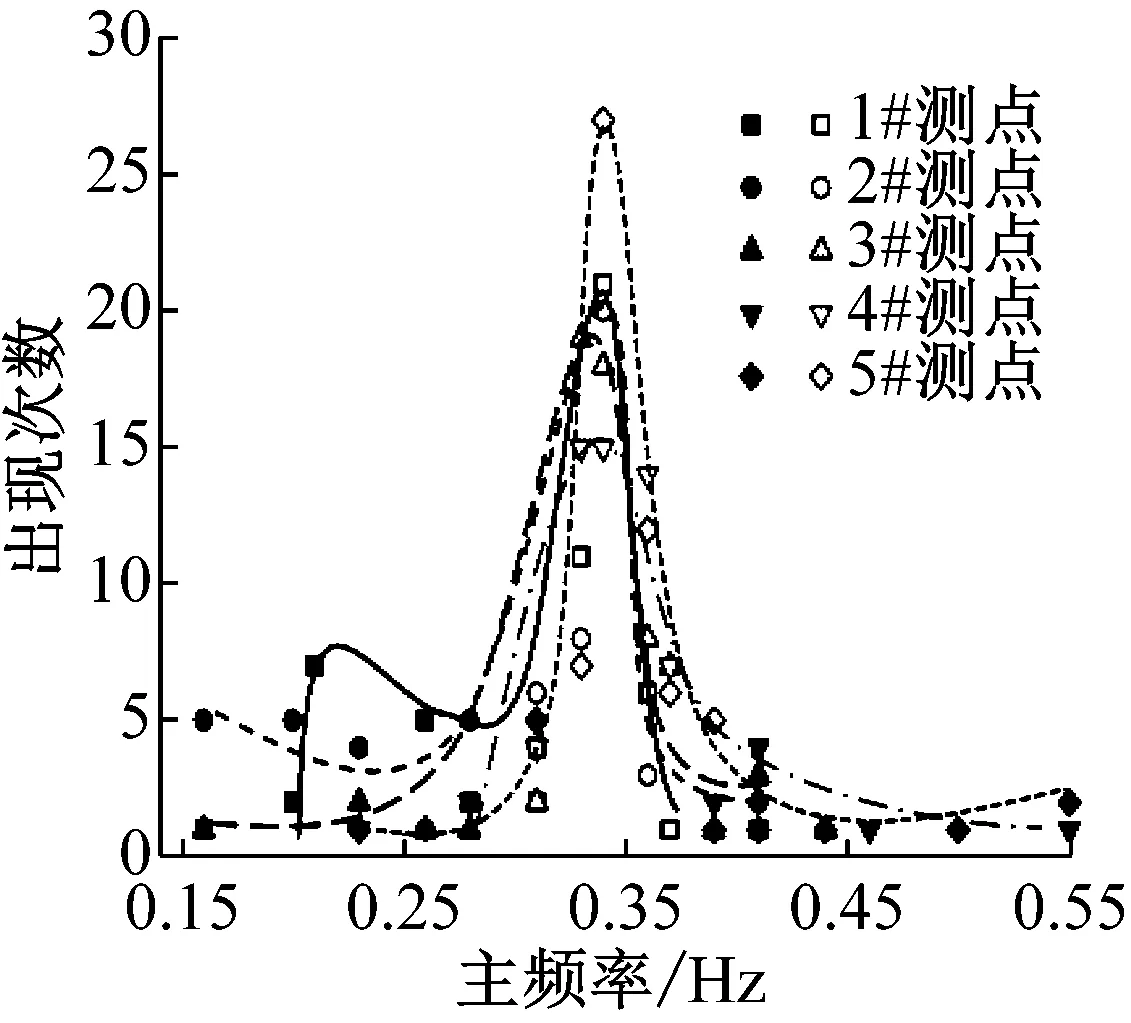
(a) 低负荷区

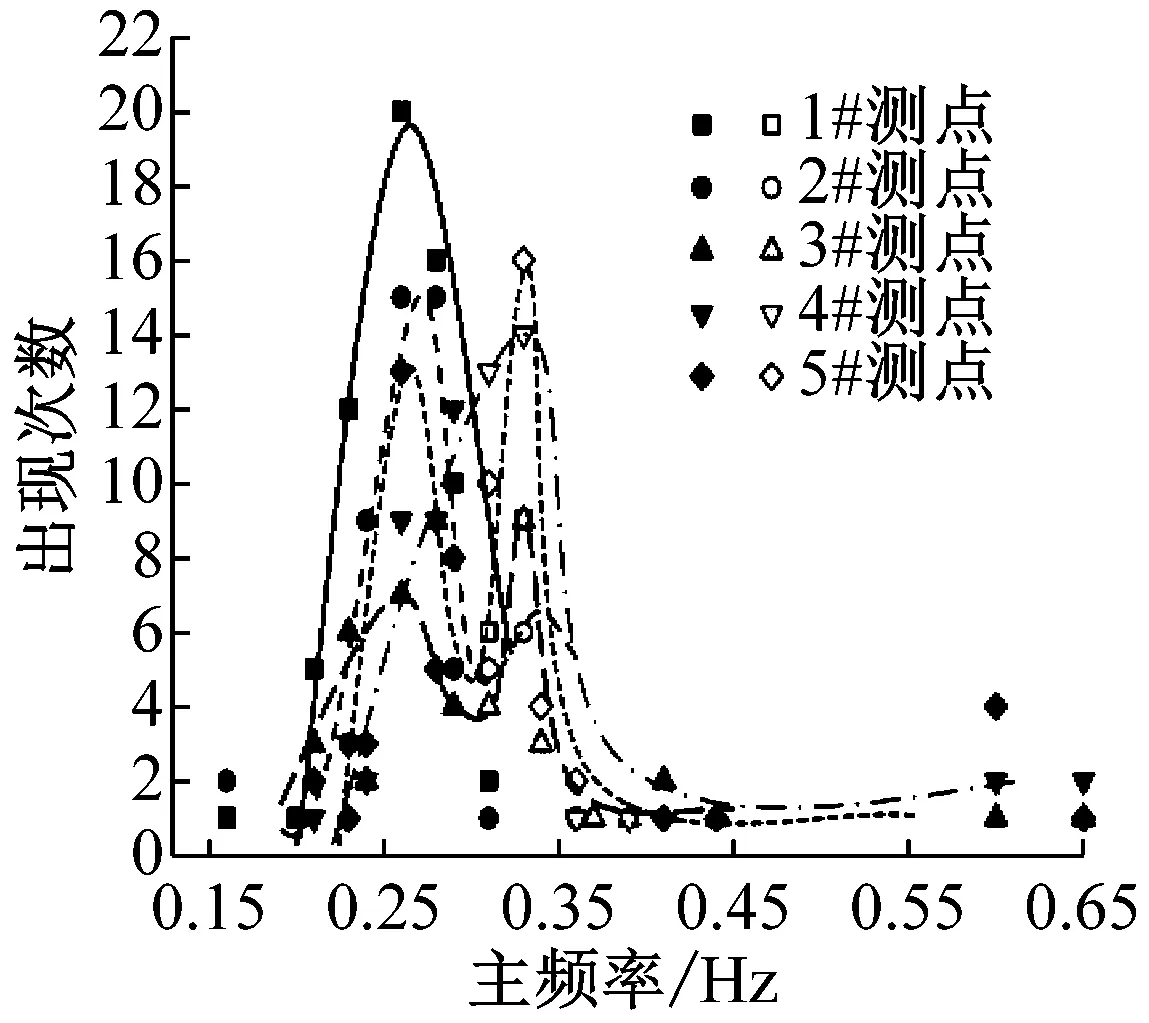
(b) 中负荷区

(c) 高负荷区

5.2各振源能量随结构位置的变化规律

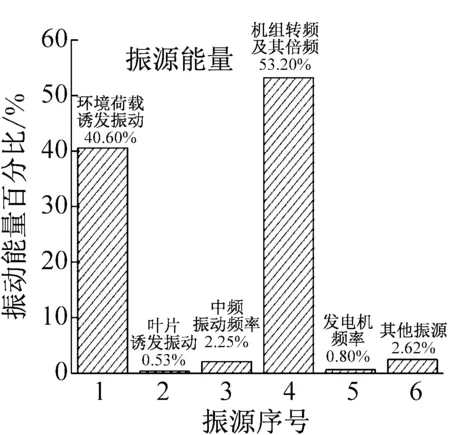
图7为运行风速6.6 m/s、叶轮转速12 r/min、机组负荷600 kW工况下风机塔筒各测点振动位移信号各主要振源成分所占能量比重分布图。该工况下风机结构处于环境荷载与谐波激励的同时作用，其振动特性主要体现这两种荷载对结构的作用特征，而从各测点的振源能量分布上来看，以环境荷载诱发结构振动及叶轮转动引起谐波激励占有振动能量的90.0%以上，最大可达到总振动能量的99.5%，发生在位于塔筒底部第一层工作平台的4#测点处，这两种振源是引起风机结构振动的强振源。

随着测点位置降低，叶轮转动引起的谐波激励对风机振动的影响在逐渐减小，能量比例从塔筒顶部1#测点处的53.2%降到了4#测点处的23.10%，说明风机运行引发谐波激励主要影响结构上部振动，由于机组距离下部结构较远导致影响减小。相对而言，由环境激励诱发结构振动能量随着测点位置的降低而逐渐增加，相应地从塔筒上部两个测点约40.0%的能量比重增加到4#测点处的76.40%，环境荷载对下部结构影响的增加一方面是由于机组运行影响的减弱，另一方面也可能是风机下部振动诱发结构多阶固有频率振动所致。除了以上两种主要振源以外，引起风机结构振动的振源还包括叶片振动诱发结构振动，发电机运行引起结构振动及电磁工频等，但由于所占能量较低，可视为风机结构振动的弱振源。

(a) 1#测点

(b) 2#测点

(c) 4#测点

5.3各主振源能量随运行因素的变化规律

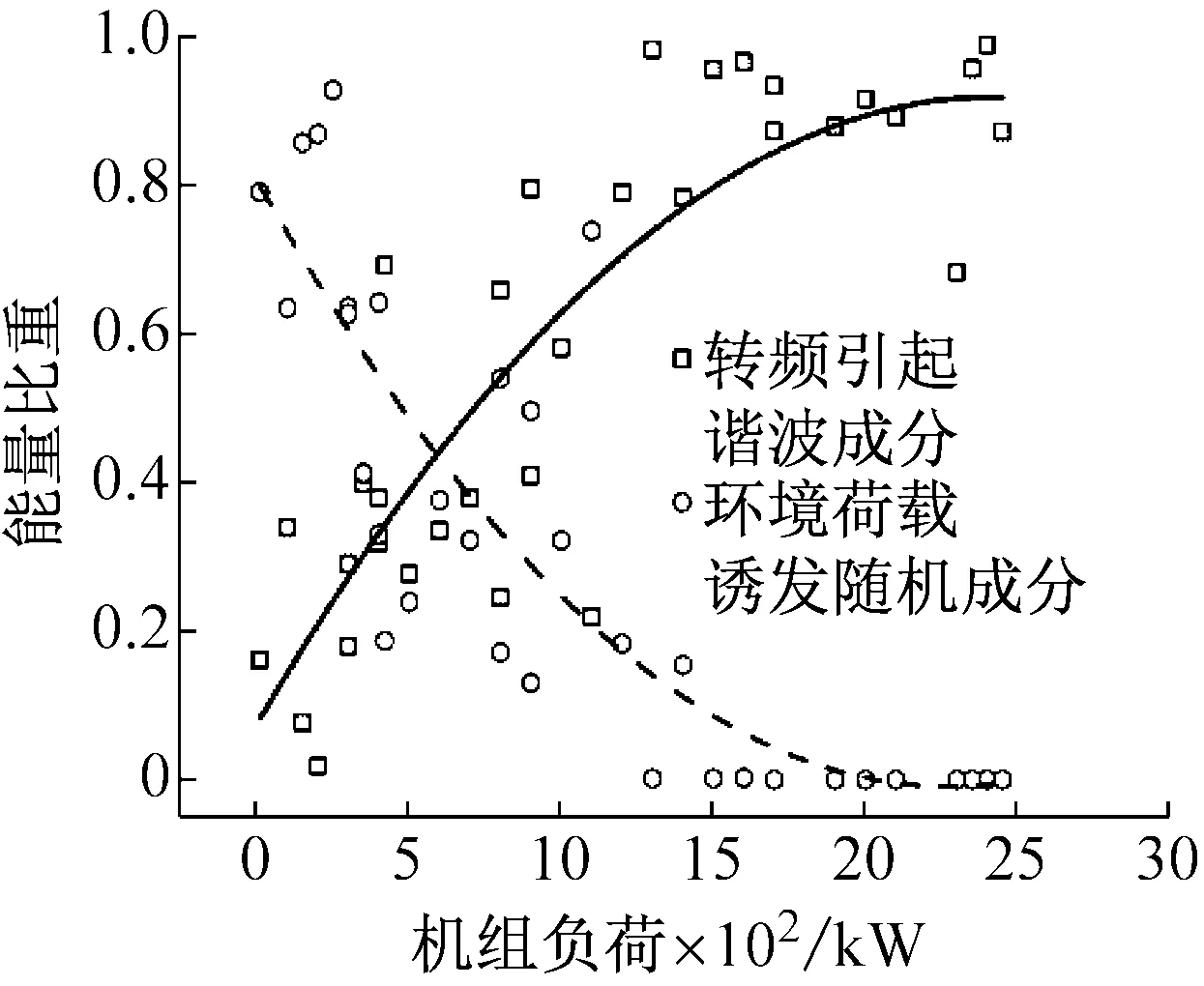
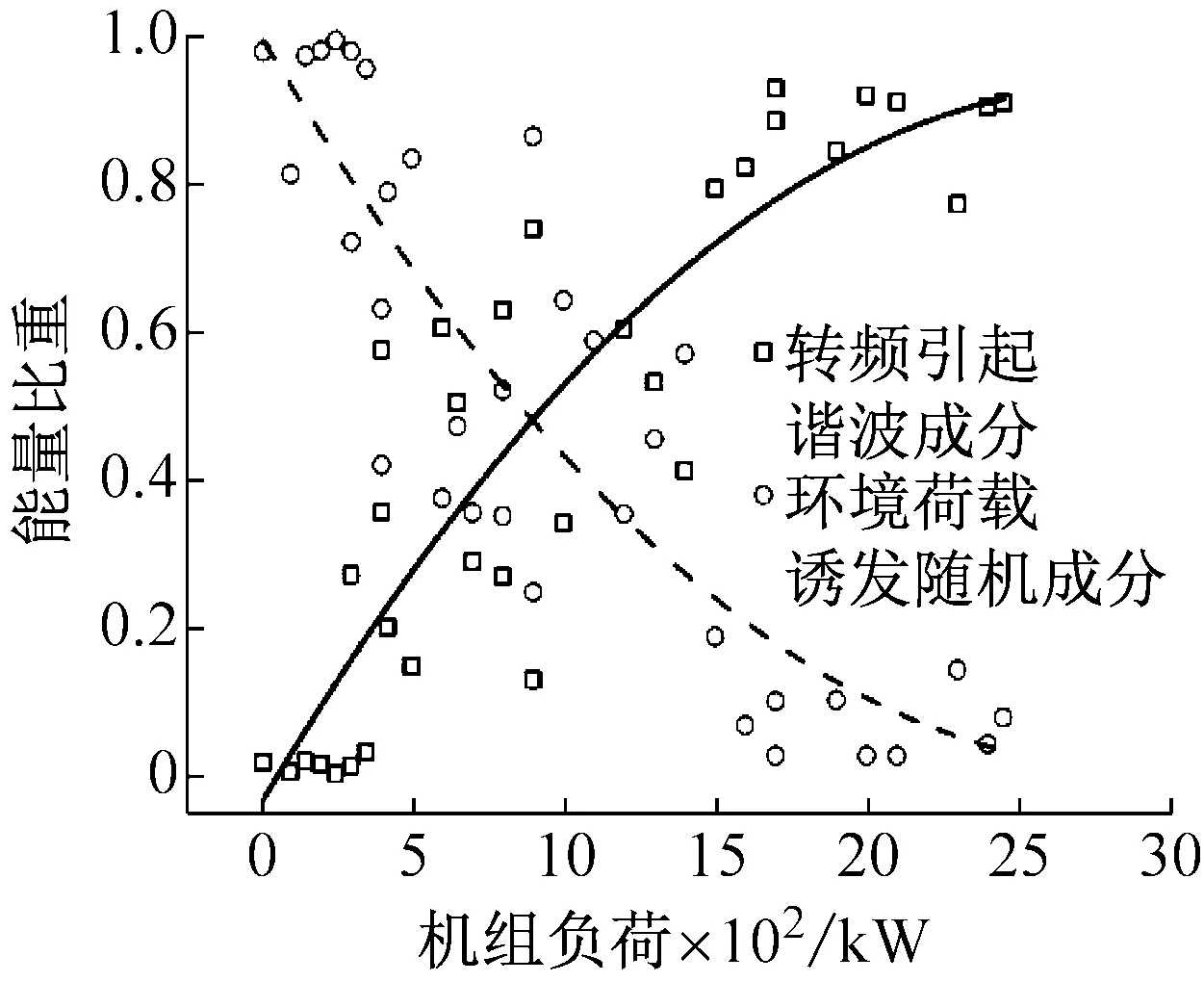
海上风机结构1#、2#和4#测点处不同主振源能量比重随机组负荷变化如图8所示。由图中可以看出结构在全负荷范围内，叶轮转动引起的谐波激励与环境荷载在内的两种主要振源所诱发结构振动的能量比重随着机组负荷变化的规律基本保持一致，均表现为谐波振源能量随着机组负荷的增加而增加，而环境荷载振源导致结构振动的能量则随着运行因素的变化而逐渐减小。这种变化的诱发原因主要是在风机结构处于较低负荷区域运行时，由于叶轮转速较低，其产生的谐波激励对结构影响有限，结构主要还是受到环境荷载作用从而在响应中体现更多结构自身的振动信息。而当机组负荷逐渐增大时，叶轮转动对结构的影响开始逐渐增大且不可忽略，这一阶段结构响应中既包括环境荷载诱发产生的随机振动，也包括谐波激励作用结构产生的受迫振动，两种振源在能量上处于较为平衡的状态。而当叶轮转速继续增加后，风机叶轮转动对结构产生的谐波影响将成为结构振动的主要振源，相比之下，环境荷载对结构的影响作用已经变得微乎其微了，在负荷大概超过1 200 kW时，结构振动基本以谐波激励下的受迫振动为主，环境荷载引起的随机成分占据的能量比重很小甚至接近于零。

(a) 1#测点

(b) 2#测点

(c) 4#测点

5.4谐波与其倍频能量随运行因素的变化规律

图9分别为风机在不同风速运行状态下，统计获得结构各振源能量在信号响应中所占比重的饼状图。由此可以看出，当运行风速刚刚超过切入风速且在4.0 m/s时，叶轮转动较为缓慢，谐波激励对风机结构影响较小，此时结构振动的主振源为环境荷载。在振动能量比重中，机组转频与倍频所占比重仅分别为0.97%与0.11%，虽在同一量级上但前者能量要大于后者。当运行风速达到6.6 m/s时，风机进入较为稳定的运行阶段，此时随着叶轮转动的加快，谐波激励占总能量比重已经超过环境荷载，机组转频能量比重达到了52.39%，而倍频能量比重仅为0.81%。虽然倍频能量比重相比于低风速下有所增加，但与转频能量的差距则进一步拉大，对风机结构产生主要影响的谐波激励振源为叶轮转动的转频，倍频激励的影响效果并不明显。当风机处于接近额定风速的11.6 m/s与接近切出风速的22.0 m/s时，风机结构均处于额定状态的运行工况，此时叶轮转动产生的谐波能量几乎占据了结构振动的全部能量，分别为98.00%与98.88%，而倍频能量比重仅为0.16%与0.12%，与前者相比微乎其微，说明风机在高负荷运行状态下叶轮转频是结构振动的最主要振源，而倍频对结构影响较小。

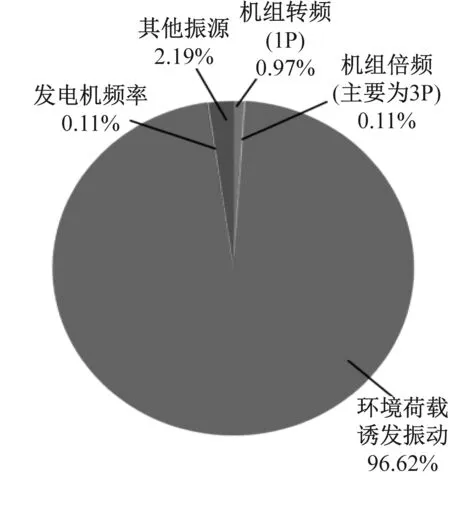
(a) 风速4.0 m/s

(b) 风速6.6 m/s

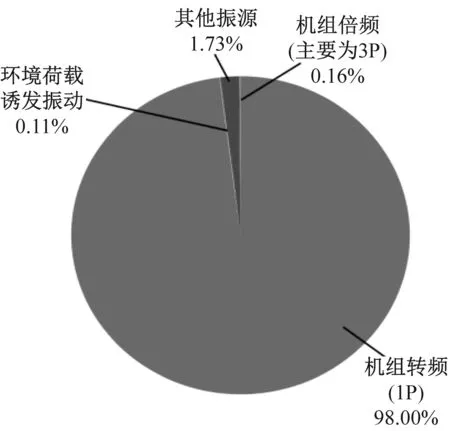
(c) 风速11.6 m/s

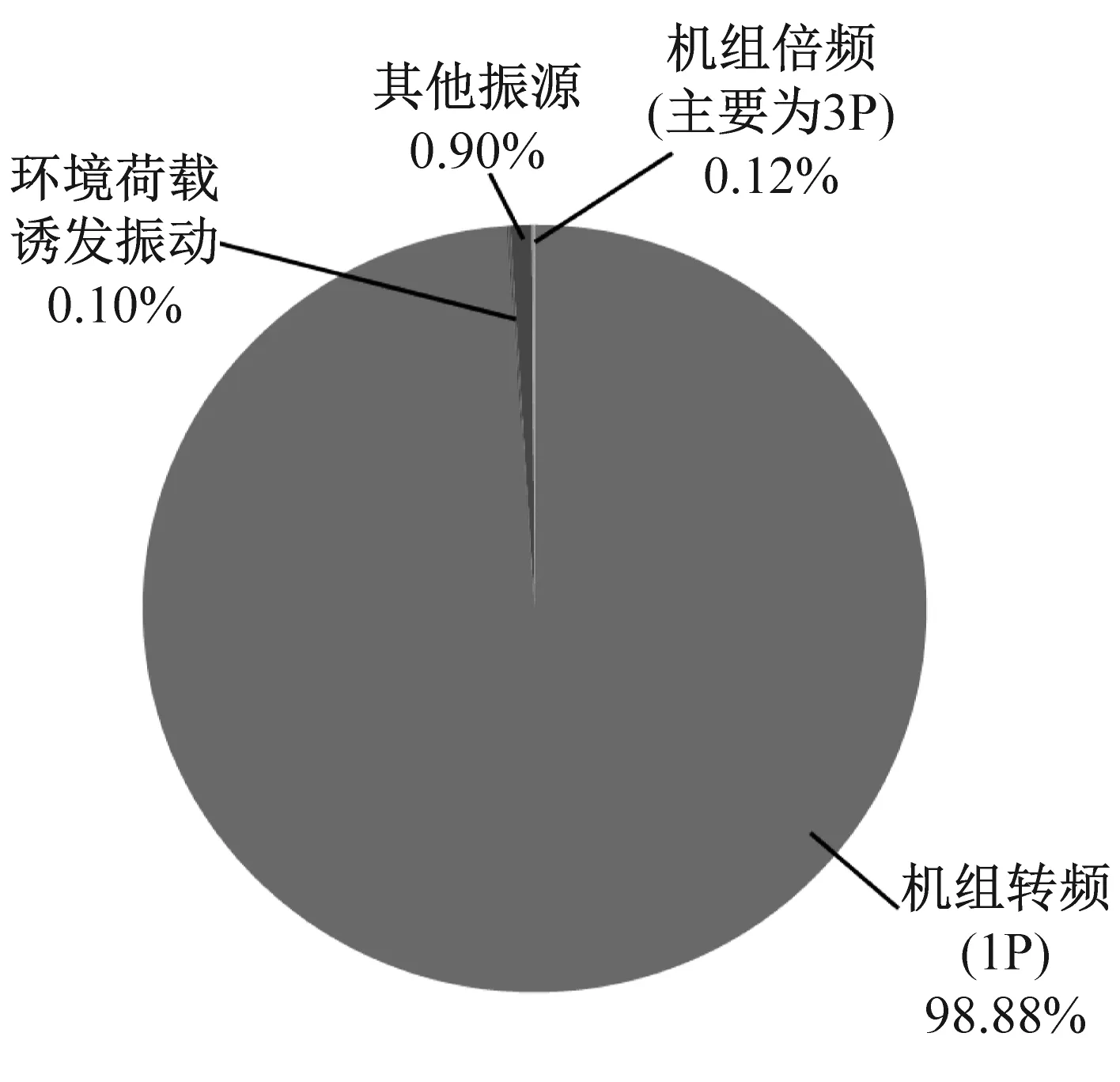
(d) 风速22.0 m/s

由以上研究可以发现，随着运行因素的增加，叶轮转动转频激励对风机结构产生的影响明显呈现增强的趋势。而将谐波振源细分后的倍频谐波激励对结构的影响则相对较小甚至可以忽略，这就说明在风机运行安全性评估中，需要重点考虑的是叶轮转动转频与结构固有模态频率间的关系。而对于倍频谐波来说，由于对结构影响效应有限，因此可以考虑在安全评估上适当地放宽固有模态频率与3P频率间的安全标准，使得风机结构在1P与3P频率间的频域安全范围加大。以上研究成果可以在风机设计过程中使得整体结构刚性化加强，固有模态频率更加远离叶轮转动转频，虽然靠近倍频频率(3P频率)而不影响结构运行的安全稳定性，为新型刚性海上风机结构基础优化设计提供了理论依据。

6 结 论

本文基于某海上风电试验样机现场实测振动数据，同时从频域和能量的角度研究运行状态下引起海上风机结构振动的主要振源及其能量分布特性随风机运行因素变化的规律机理，主要获得以下结论：

(1) 在运行状态下对风机振动影响最为关键的振源是环境激励与叶轮转动产生的谐波激励，前者主要体现结构自身的低阶模态成分，而后者则主要呈现机组转频及其倍频信息。

(2) 随着运行风速和机组负荷的增加海上风机结构振动的主振源变化遵循由单一的环境荷载激励转为环境荷载激励和叶轮转动联合作用再到完全由叶轮转动引起谐波激励影响的规律。

(3) 随着测点位置的降低，谐波激励对风机振动的影响在逐渐减小，说明其主要影响结构上部的振动，而由环境荷载激励引发的结构振动能量随着测点位置的降低而逐渐增加。

(4) 海上风机结构在全负荷范围内，各测点谐波振源能量随着机组负荷的增加而增加，而环境荷载振源导致结构随机振动的能量则随着运行因素的变化而逐渐减小。

(5) 将谐波振源细分后的谐波倍频(主要为3P频率)激励对结构的影响远小于叶轮转动对应的谐波基频(1P频率)的影响，因此在风机运行安全性评估中需重点考虑的是叶轮谐波基频激励与结构固有模态频率间的关系，而适当地放宽固有模态频率与对结构影响有限的倍频间的安全标准，增大风机结构在1P与3P频率间的频域安全范围而不影响结构运行的安全稳定性。

[1] 陈小波，李静，陈健云.海上风电机组随机风浪荷载时程数值计算[J].太阳能学报，2011，32(3)：288-295.

CHEN Xiaobo, LI Jing, CHEN Jianyun. Numerical calculation of random wind and wave loads time history of offshore wind turbine[J]. Acta Energiae Solaris Sinica, 2011,32(3): 288-295.

[2] MARINO E, BORRI C, PEIL U. Offshore wind turbines: a wind-fully nonlinear waves integrated model[C]. The Fifth International Symposium on Computational Wind Engineering, Chapel Hill, North Carolina, USA, 2010: 23-27.

[3] 刘志强.海上风力发电支撑体系在环境荷载作用下动力响应分析[D].大连：大连理工大学，2008.

[4] ANDREW SWARTZ R, LYNCH J P, ZERBST S, et al. Structural monitoring of wind turbines using wireless sensor networks[J].Smart Structure and Systems,2010,6(3):1-14.

[5] 马人乐，马跃强，刘慧群，等. 风电机组塔筒模态的环境脉动实测与数值模拟研究[J].振动与冲击，2011，30(5)：152-155.

MA Renle, MA Yueqiang, LIU Huiqun, et al. Ambient vibration test and numerical simulation for modes of wind turbine towers[J].Joumal of Vibration and Shock,2011,30(5):152-155.

[6] VRABIE V D, GRANJON P, SERVIERE C. Spectral kurtosis: from definition to application[C]. In the Proceedings of the Sixth IEEE NSPI Grado-Trieste, Italy, 2003.

[7] DION J L, STEPHAN C, CHEVALLIER G, et al. Tracking and removing modulated sinusoidal components: A solution based on the kurtosis and the Extended Kalman Filter[J]. Mechanical Systems and Signal Processing, 2013, 38:428-439.

[8] DION J L, TAWFIQ I, CHEVALLIER G. Harmonic component detection: Optimized Spectral Kurtosis for operational modal analysis[J]. Mechanical Systems and Signal Processing, 2012, 26:24-33.

[9] HUANG N E, SHEN Z. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time analysis[C]. Proceedings of the Royal Society of London, Series A. 1998, 454:903-995.

[10] KOOSINIS Y, MCLAUGHLIN S. Investigation and performance enhancement of the empirical mode decomposition method based on a Heuristic search optimization approach[J]. Transactions on Signal Processing, 2008, 56(1):1-13.

[11] 穆钢，史坤鹏，安军，等.结合经验模态分解的信号能量法及其在低频振荡中的应用[J].中国电机工程学报，2008，28(19)：36-41.

MU Gang, SHI Kunpeng, Anjun, et al. Signal energy method based on EMD and its application to research of low frequency oscillations[J]. Proceedings of the CSEE, 2008, 28(19): 36-41.

[12] 袁浩东.基于振动能量的故障诊断方法研究[D].郑州：郑州大学，2012.

[13] 张超，陈建军，郭讯.基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击，2010，29(10)：216-220.

ZHANG Chao, CHEN Jianjun, GUO Xun. A gear fault diagnosis method based on EMD energy entropy and SVM[J]. Joumal of Vibration and Shock, 2010,29(10):216-220.

[14] LIAN Jijian, SUN Liqiang, ZHANG Jinfeng et al. Bearing capacity and technical advantages of composite bucket foundation of offshore wind turbines[J]. Transactions of Tianjin University, 2011,17: 132-137.

[15] LIAN Jijian, DING Hongyan, ZHANG Puyang, et al. Design of Large-scale prestressing bucket foundation for offshore wind turbines[J]. Transactions of Tianjin University, 2012,18: 79-84.

[16] DONG Xiaofeng, LIAN Jijian, YANG Min, et al. Operational modal identification of offshore wind turbine structure based on modified SSI method considering harmonic interference[J]. Journal of Renewable and Sustainable Energy, 2014, 6(3): 033128(1-29).

[17] 董霄峰. 海上风机结构振动特性分析与动态参数识别研究[D]. 天津：天津大学，2015.

Vibrationsourcefeaturesofoffshorewindpowerstructuresunderoperationalconditions

DONG Xiaofeng1,2, LIAN Jijian1,2, WANG Haijun1,2

(1.State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China; 2. Frontier Technology Research Institute Limited Company, Tianjin University, Tianjin 301700, China)

Due to the operational environment complexity of offshore wind power structures, the correct identification of their vibration sources and their vibration source features study become key problems for their operation security assessments. Here, a new type test prototype of offshore wind turbine with a composite cylindrical foundation structure was taken as the study object, according to vibration response data at the structure’s different positions measured on the original prototype under the condition of full loading, its vibration sources to excite structural vibrations under different operational conditions were identified and analyzed. Firstly, the main vibration sources causing structural vibrations of the offshore wind turbine, and frequency domain properties of the corresponding vibration responses were identified with the spectral kurtosis (SK) method. Secondly, the measured signals were decomposed using the empirical mode decomposition (EMD) method to obtain components in frequency domain or frequency scale characterizing different vibration sources’ features. Simultaneously, the vibration energy method was introduced to analyze statistically energy proportions of various vibration sources. At last, the distribution laws of the main vibration sources of the offshore wind turbine’s entire structure under operation and the relevant vibration energy with the variation of operational factors were derived. The study showed that the vibration sources of the offshore wind turbine under operation have a variation law from pure environmental load excitations to the combination of ambient loads and its impeller rotating, and finally to harmonic component excitations caused by its impeller rotating.

offshore wind power; site measurement; vibration source identification; spectral kurtosis (SK); empirical mode decomposition (EMD); vibrational energy

国家创新研究群体科学基金(51021004)；高等学校学科创新引智计划(B14012)

2016-04-07 修改稿收到日期：2016-06-09

董霄峰 男，博士，讲师，1986年8月生

练继建 男，教授，博士生导师，1965年8月生 E-mail: tju_dongxf@126.com

TK8

： A

10.13465/j.cnki.jvs.2017.17.004