基于改进的BP神经网络和小波奇异值的交通事件检测
2017-09-23王宝国李渊韬胡彤宇张军朱新山杨正瓴
王宝国+李渊韬+胡彤宇+张军+朱新山+杨正瓴

引言
道路上偶然发生的一些事件,譬如故障停车、货物散落、渣土洒落等引起的交通拥堵以及交通事故等,这些统称为交通事件。因为交通事件的发生带有一定的随机性,所以这些交通事件发生的时间和地点也都是不能预测的。
当事件确定已经发生过,此时进行的事件检测就是交通事件检测,它应该检测出交通事件所发生的位置以及类型。我们可以通过一些人工方式进行检测,例如紧急电话、巡逻车等,但考虑到人工方式检测总体反应时间较长,交管部门无法及时了解道路交通状况,容易引起交通堵塞,这对整个道路交通管理会带来不便。自动事件检测(AID)方法可以很好的帮助交通管理部门快速的处理交通事件或者交通异常。自动事件检测(AID)能够实时获取交通场景的信息,快速检测交通事件的发生,从而交通管理部门能够随时实施相应的管理手段以及交通控制,迅速处理已经发生的交通事件,这样可以降低发生二次交通事故的概率,也保证了交通运行安全。
交通事件自动检测算法可分为“间接检测算法”和“直接检测算法”两大类。间接检测算法应用广泛,主要包括模式识别方法和统计方法。在模式识别方法中又以California算法系列和Mcmaster算法应用最广。统计方法主要包括指数平滑法、时间序列算法和贝叶斯算法等。近年来随着神经网络的广泛应用,出现了很多以神经网络为基础的事件检测算法。
传统的交通事件检测算法存在着以下不足:检测效率低、误报率高等。同时由于算法的局限性很难应用在城市中比较复杂的道路上;上述有些智能算法由于阈值或临界值的设置通常十分困难,具备经验性,且其取值直接影响到算法的检测效率和效果,因而这将成为这些算法的最大制约因素。传统的小波分析提取故障特征的过程中受到小波基和分解层数选取的影响较大,不利于故障类型的识别。
为了克服上述方法的不足,充分考虑交通环境的复杂性和交通信号时间序列的非线性特点,本文在以上算法的基础上提出了一种基于改进的BP神经网络和小波奇异值的方法进行交通事件检测。
1方法
1.1算法基本思想
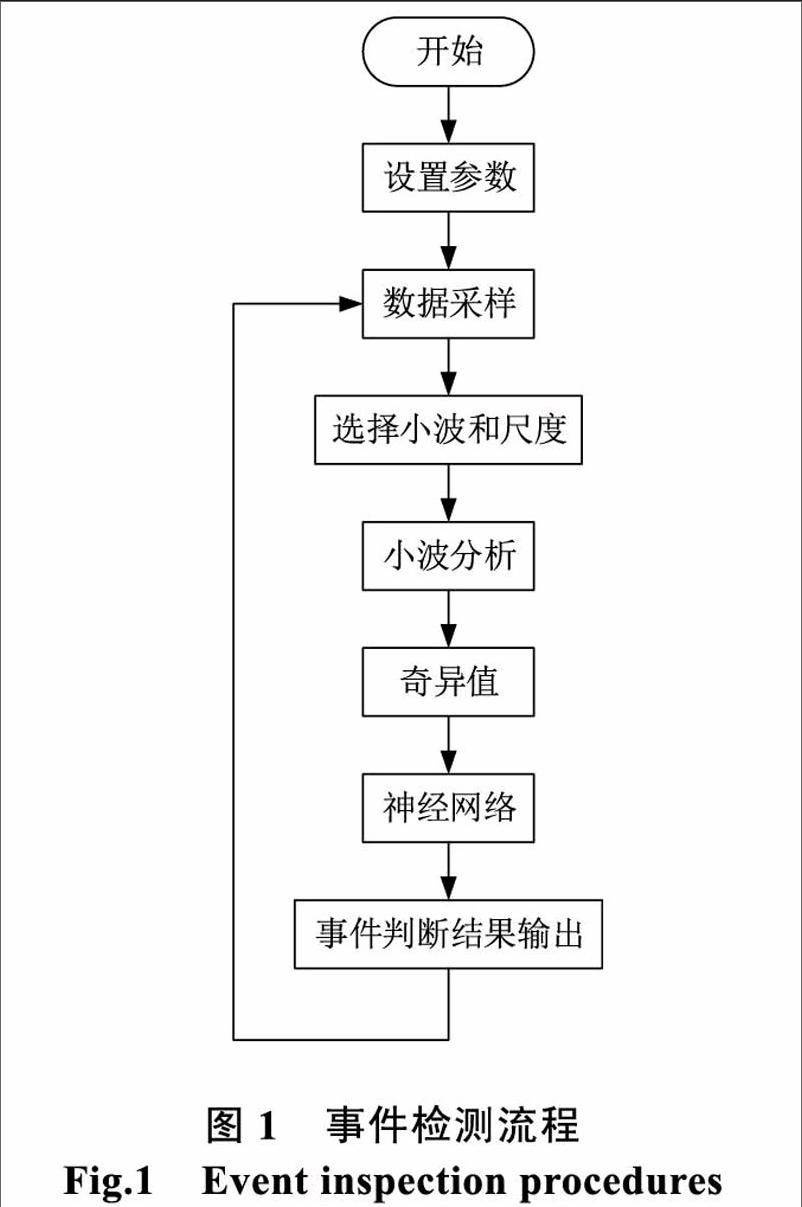
在交通事件发生点,交通流参数将发生变化。通过车辆检测器采集车流的相关信息,利用小波变换对输入信号进行预处理并求解其奇异点,奇异点就是事件发生点,然后通过神经网络对奇异点进行分类从而判断事件类型。算法流程如图1所示:
本方法的具体实施步骤如下。
(1)将获取到的交通流进行小波分解,获取小波细节系数;
(2)通过相重构技术将小波系数向量重构成特征矩阵,并对其进行奇异值分解,获取小波奇异值;
(3)将小波奇异值输入到神经网络进行学习訓练,进行交通事件类型识别。
1.2BP神经网络的基本理论
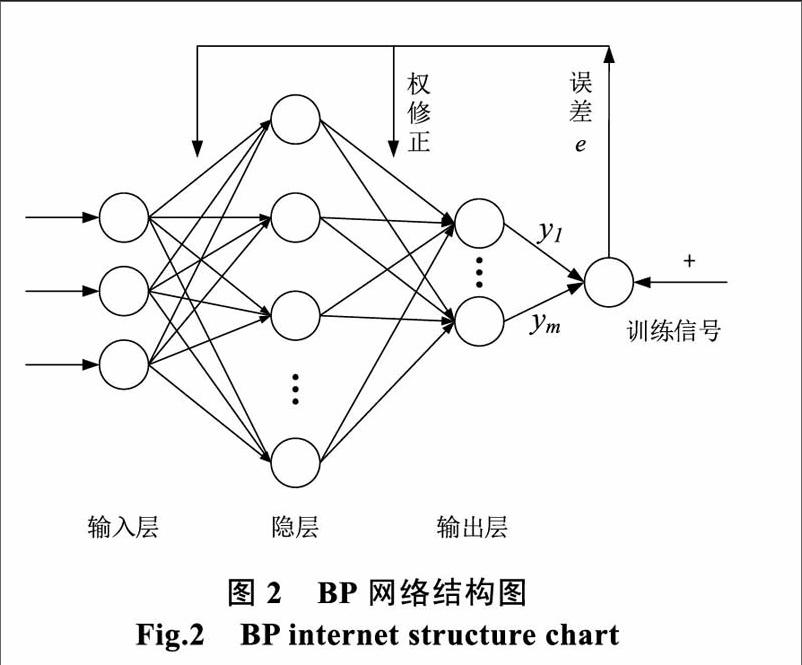
在系统中搭建如图2所示的具有反馈结构的三层BP神经网络,包含输入层、隐层和输出层。由于具有至少一个S型函数隐层的网络能够逼近任何有理函数,增加层数虽然可以进一步降低误差,提高精度,但同时也使网络复杂化,增加网络权值的训练时间。而精度的提高实际上也可以通过增加隐层中的神经元数目来获得,且其训练效果比增加层数更容易观察和调整。所以本文最终选取三层神经网络结构。
1.2.1BP网络结构参数的确定
将采集到的数据通过小波分析进行奇异点检测,提取高频系数d作为神经网络的输入。网络隐层神经元的个数n决定了整个网络的学习速率和精度,隐层神经元个数n与输入层神经元个数n的关系可以由Kolmogorov定理得到,如下式(1)所示。
结合式(1)和式(2)选取合适的n值进行网络的训练,如果不能满足训练要求,则在一定的范围内调整n的取值,直至达到训练要求。
1.2.2 BP网络的学习过程
BP网络的学习过程由正向传播和反向传播组成。在正向传播过程中,输入信号从输入层经隐层神经元逐层处理,并传向输出层,每一层神经元的状态只影响下一层神经元的状态,各神经元间的传递函数采用sigmoid函数:
如果在输出层不能得到期望的输出,则转向反向传播,将输出的误差e按原来的连接通路返回。通过修改各层神经元之间的权值wij,和神经元的阈值H,使得误差信号最小。得到合适的网络权值和阈值之后,便可对新样本进行非线性映射。
为克服BP网络收敛速度慢和易陷入局部极小值的缺陷,本文采用附加动量法和自适应学习率。在网络训练的第n次循环中权值e,和阈值e,的改变量按带动量项的最速下降法则进行,即:
自适应学习速率有利于缩短学习时间。对于一个特定的问题,要选择适当的学习速率不是一件容易的事情。训练初期功效较好的学习速率,不见得适合后来的训练。通常调节学习速率的准则是:检查权值的修正值是否真的降低了误差函数,如果确实如此,则说明选取的学习速率值小了,可以对其增加一个量。若不是这样,则产生了过调,那么就应该减少学习速率的值。下面给出了一种自适应学习速率的调整公式:
此方法可以保证网络总是以网络可以接受的最大的学习速率进行训练。当一个较大的学习速率仍能够使网络稳定学习,使其误差继续下降,则增加学习速率,使其以更大的学习速率进行学习,一旦学习速率调的过大,而不能保证误差继续减少,则减小学习速率,直到学习稳定为止。
1.3交通流小波奇异值的获取
小波分析在处理突变信号方面表现突出,有着很好的时频特性和局部特性。小波分析在信号的高频部分可以取得较好的时间分辨率,在信号的低频部分可以获得较好的频率分辨率,从而能有效的从信号中提取信息。
1.3.1信号的小波变换和变换系数为连续小波变换。
在连续小波变换中考虑两参数函数族:
在许多应用中,特别是在信号处理中,数据用有限数目的值表示,所以重要的是考虑连续小波变换的离散情形。endprint
信号中不规则地突变部分和奇异点往往包含比较重要的信息,它是信号重要特征之一。小波分析具有空间局部化性质,可有效地分析信号的奇异性。
奇异值具有良好的稳定性、比例不变性、旋转不变性和降维压缩特性。将矩阵进行奇异值分解,再通过奇异值降维压缩可获得矩阵的有效秩,这里的有效秩为所保留的奇异值的个数。奇异值的这些特性能有效地反应矩阵的特征。
1.3.3提取交通流奇异值
小波奇异值的获取可分为以下步骤:
(1)对原始交通流信号进行一定层数的小波分解;
(2)根据小波细节系数向量构成特征矩阵;这里特征矩阵的形成采用相重构技术。假设交通流信号为重构的吸引子矩阵为:
(3)对上一步中得到的特征矩阵进行奇异值分解,提取小波奇异值。
2实例验证
2.1数据采集背景
在天津市一个快速路段全线每隔500-1000 m(本文选用1000 m)布设车辆检测器,现场检测各路段的交通流参数。由于采样周期必须小于事件周期,数据采样间隔选为60 s。交通流参数选用交通密度。在检测路段的上游和下游各布设一套检测器(如下图3所示),将单位时间内上下游检测器测量数据的差值作为系统检测的输入。
2.2事件检测算法
一般情况下,当交通密度小于25辆/(km·车道)时,交通流较为顺畅,其相应的车速大约为64km/h。当交通密度大于25辆/(km·车道)时,则从繁密交通向拥挤交通过渡,如果超过47辆/(km·车道),将出现严重拥挤。因此设定25辆/(km·车道)为事件判断的阈值。
按交通密度大小将交通事件分为四类:正常交通(A)、交通拥挤(B)、拥挤加剧(C)、拥挤减缓(D)。通常认为交通密度K≤25辆/(km·车道)的交通流量为顺畅状态,K≥47/(km·车道)交通开始拥挤。四个状态与交通密度的对应关系可用表1来反应:
2.3 MATLAB仿真
利用采集到的交通流数据进行MATLAB仿真,通过对上下游检测器的模拟数据进行二尺度小波分解,得到二尺度高频系数,然后把这些数据输入到神经网络中进行训练。本实验共设20000个样本,其中15000个用于训练,5000个用于检验,正确识别4813个,即检测率为96.26%。部分检测结果如表2所示。
3结语
根据检测结果可以看出,将小波分析与BP神经網络结合能很好的检测交通事件并给出交通事件的分类信息。用BP神经网络对交通事件进行分类,为解决BP神经网络收敛速度慢和易陷入局部极小值的问题,本文采用了附加动量法和自适应学习率调整法相结合的方法。此算法结合了小波分析在信号处理方面的优越性,在算法中将信号的奇异点即交通事件发生点提取出来,取得了很好的效果。考虑到原始交通流数据集的不平衡性和数据源过于单一化应采用文献介绍的基于多源数据的城市道路交通事件检测和利用重采样、基于特征加权的检测方法,有望获得更好的检测效果。endprint
