基于乘客均衡候车的轨道交通协同限流建模

马 羽，王卓群，温少表，罗 钦,3

1)深圳地铁集团有限公司运营总部客运一分公司，广东深圳 518071；2)深圳大学城市轨道交通学院，广东深圳 518060；3)深圳技术大学城市交通与物流学院，广东深圳 518118

【交通物流/TransportationLogistics】

基于乘客均衡候车的轨道交通协同限流建模

马 羽1，王卓群2，温少表1，罗 钦2,3

1)深圳地铁集团有限公司运营总部客运一分公司，广东深圳 518071；2)深圳大学城市轨道交通学院，广东深圳 518060；3)深圳技术大学城市交通与物流学院，广东深圳 518118

城市轨道交通大客流呈现非均衡、非稳态、非线性特征，直接影响乘客服务水平和列车运行可靠性，是车站客运组织管理中的重要环节．在分析大客流条件下乘客候车延误影响因素的基础上，考虑列车周期性运行特性，并抽象乘客到达规律符合均匀分布，以各站乘客均衡候车为优化目标，构建线路层车站间的单目标多约束协同限流模型，并基于Matlab非线性规划fmincon函数进行求解．算例分析结果表明，该方法能从线路大客流均衡管控的角度缓解运能与运量之间的矛盾，避免局部车站客流积压严重，具有有效性和合理性．

城市轨道交通；大客流；均衡候车; 多站协同；限流；出行体验

图1 车站客流与运力相互作用关系Fig.1 Interaction between passenger flow and capacity of rail station

近年来，随着中国轨道交通的持续快速发展，北京、上海、广州及深圳等地轨道交通正步入网络化运营阶段，轨道交通在城市客运中发挥着日趋显著的作用．客流大幅增长，特别是高峰时段客流量更大、到达时间更集中且方向性明显，导致需求与运输能力不匹配的矛盾日益突出，客流拥挤和乘客滞留问题严重．此外，自然灾害、事故、车辆故障和人为破坏等重大突发事件也可能引发车站大量乘客的滞留，形成大客流．大客流事件对于轨道交通系统的运营管理提出挑战，并有特殊要求；在大客流事件发生期间，若不采取相应的应急措施，将影响列车安全运行和准点到达，甚至可能发生人员伤亡等意外事件发生．为此，轨道交通运营管理部门采取一系列措施来保障运营的安全和可靠，其中，“限流”——通过一定时间内限制进站上车或换乘通行的客流量，已成为一种最常用的管理方式．当前采用的限流方法大多面向单一车站，即以大客流车站进出站人数作为划分拥挤等级程度的标准，不同的等级对应着不同的限流方案．如站台限流、站厅限流，甚至站外限流．单站客流的容纳量主要取决于该站站台面积、站厅面积，扶手梯、电梯、楼梯的数量及相应的承载能力等，各影响因素之间的相互作用如图1所示．单站限流能有效保障车站运营的安全与有序，但有一定的局限性．解决大客流问题的根本方法在于如何合理利用列车和车站的运输能力，在较短的时间内实现客流的有效疏散．但当部分车站进站客流较大，而列车到达车站的车载剩余能力又极其有限时，将造成此类车站乘客大量滞留并造成候车时间过长，从而带来较大安全隐患和服务水平的大幅下降．因此，有必要从全线综合考虑相关车站单位时间进站客流和列车能力利用率，实现基于乘客均衡候车的多站大客流协同管控．

目前，针对大客流等待时间优化的相关研究较少，成果多集中于影响客流等待时间的要素分析．施云惠等[1]提出完整的城市轨道交通线路层、路网层拥挤度指标体系并给出计算方法；郑雪梅等[2]通过构建站点系统动力学模型对车站现状进行仿真实验，模拟客流在站内设施的分布及其动态变化过程，进而明确当前客流拥堵的关键位置及拥堵成因；肖慧雅等[3]对地铁站现有限流设施的不足之处进行分析，并提出相应的改进措施；姚向明等[4]从线网层面考虑建立客流需求与输送能力匹配度最大化和延误客流量最小化的多目标数学规划模型，以求得各站最佳进站客流量；曹志超等[5]利用排队论方法提出一种严重拥挤情况下基于列车时刻的乘客等待时间模型；张正等[6]通过分析限流的作用和影响因素，提出车站间协同限流及相关参数的计算方法；赵鹏等[7]应用数学规划方法构建以乘客延误损失最小化和客运周转量最大化为目标的线路层车站间及时段间协调控制模型．李伟等[8]则从列车运营角度出发，通过协调轨道网络中列车的发车时间，使网络客流运输效率最大．上述成果为研究轨道交通大客流管控方法提供了有益的借鉴，本研究通过分析城市轨道交通大客流条件下乘客候车延误机理，确定影响乘客等待时间的主要因素，在此基础上考虑线路层各车站到达人数与列车运输能力的相互影响，构建乘客候车时间均衡为优化目标的多站协同限流模型．

1 大客流情况下的乘客候车延误分析

城市轨道交通客流具有非均衡、非稳态及非线性等复杂特征，主要表现在客流起讫点分布的多样性、到达时间的随机性、以及受站车能力的限制性[9-10]．基于多站协同管控的思想，本研究统筹考虑线路高峰时段客流分布状况，从乘客候车时间均衡的角度，把计算各站客流最佳上车人数作为车站实施限流的依据．最佳上车人数指通过线路协同限流使得各站乘客在高峰时段内的候车时间趋于均匀，避免线路部分站点由于到站列车车厢剩余运力不足，导致乘客长时间无法上车而造成乘客大量滞留．由于城市轨道交通列车提供周期性运行服务，乘客在达到站台后面临列车车厢剩余承载能力不足而产生留乘，则需等待1～i(i=2,3,…,n)个列车周期．因此，对于单个车站而言，如不能有效协调进站与上车人数的关系，会导致滞留乘客总数随时间推移而增加，受延误影响乘客越来越多，延误影响范围逐周期扩大[11-14]．

大客流引起的候车延误与乘客到达率λ(t)、 乘客流量函数q(t)及列车周期T相关．其中，列车周期T与列车发车间隔td及列车停站时间tw有关，T=td+tw；q(t)与列车车厢剩余承载能力以及车站乘客上下车率相关．因此，在k个周期时间内，第j站乘客在某出行方向上的总滞留人数为

(1)

2 多站协同限流模型构建与求解

2.1模型假设与变量定义

为简化模型，本研究做如下假设：

1)已知高峰时段客流需求量及起讫点(下称OD点)．考虑到高峰时段客流组成多为通勤客流，其结构稳定，可通过历史数据分析获得较高精度的OD客流信息；

2)列车按计划时刻表运行，无晚点或其他突发事件发生；

3)假设进站客流为同一控制时间段内均匀到达，状态稳定；

4)乘客可正常上车，不受下车客流的逆向影响；

5)客流需求总量保持不变，即计算客流不考虑转移到其他交通方式．

2.2变量定义与模型构建

基于2.1节的假设，定义影响候车时间的相关参数如下：Hi为第i个控制时间段时长；Dij为第i个控制时间段第j站到达的乘客总人量；Sij为第i个控制时间段第j站各次列车允许的上车人数；z为客流分解点(即列车通过该客流分解点后运能快速释放)；Qij为列车在第i个控制时间段第j站各次列车的剩余容纳能力(单位：人)；C为列车定员人数；αj为乘客在第j站下车率(单位：人)；Pij为第i个控制时间段内首次列车到站时第j站的候车人数；λij为第i个控制时间段内第j站客流均匀到达率(单位：人)；T为列车发车时间间隔(单位：min)．

下面以各控制时间段(第i周期)全线j站等待时间最小且均衡为目标，构建多站协同限流模型，如式(2)至式(5)．

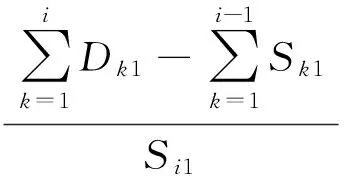
(2)

(3)

(4)

(5)

(6)

Sij≤min(Qij,Pij)

(7)

其中，式(3)表示列车在各控制时间段内各次列车在各站剩余能力，是上车客流人数的限制条件，列车总承载量为列车定员人数与满载系数的乘积；式(4)表示第j站在第i个控制时间段内客流平均到达率；式(5)表示第j站在第i个控制时间段内可开行的列车对数；式(6)表示各控制时间段内首次列车到站时各站的候车人数；式(7)为最佳上车人数的约束条件，该值既应满足客流需求上限约束，即上车人数不能超过当前候车人数，同时又满足列车剩余能力的上限，即不能超过列车可容纳量．

2.3求解算法

式(2)至式(5)为单目标非线性数学模型，约束条件为线性不等式，可用Matlab的非线性规划fmincon函数进行求解，逐次递推得到各分时间段内各站最佳上车人数以及客流平均等待周期、平均控流率等指标．其中，控流率为车站在控制时段内不能满足的客流需求与实际客流需求的比值．

3 多站协同限流模型构建与求解

3.1基本信息

以某轨道交通线路为例，包含A—Q共17个车站，假设控制时段为早高峰07∶30—08∶30，仅考虑从A到Q单一运行方向，该时段内最大断面为J—K，断面客流达4万人次．表1为分时段各车站客流需求量，其他相关参数取值如表2．由表1可见，各站及分时段的客流需求不均衡性都较大，主要集中在A站至J站和07∶30—08∶00．自K站开始，列车运能紧张问题得以快速缓解，乘客无需留乘．线路呈现出的客流分布特点使列车在前方运行区间运能被快速占用，导致后方车站乘客大量滞留，需等待多个列车周期．若不从线路协同角度实施大客流管控，将对部分车站乘客出行体验和客运组织带来较大冲击．

表1 各时段车站客流需求量(单方向进站人数)

3.2结果分析

由表2可见，A和B站客流需求量一般，C—J站客流需求较大，自K站起，客流分解，无需限流．经初步推算，如不采取限流措施，列车到达G站时将会满载，后方车站乘客很难上车．因此，控流车站选定为A—J共10个车站．运用Matlab的fmincon函数对算例进行求解，计得车站分时段最佳上车人数如表3．

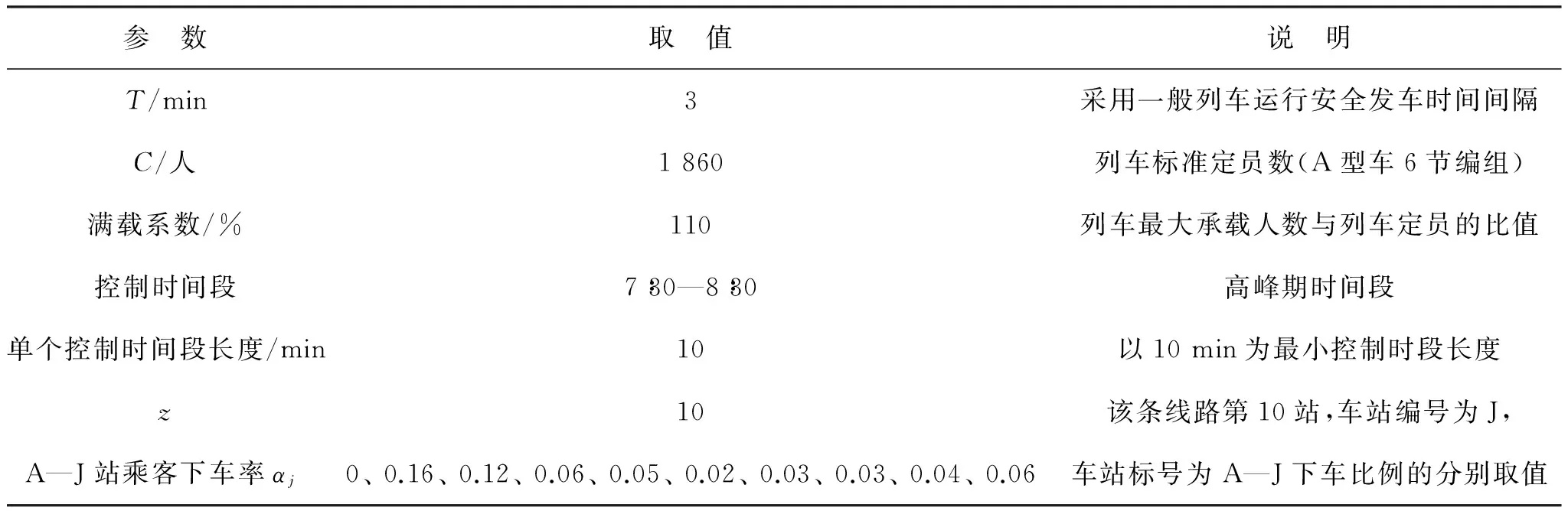
表2 本算例相关参数

表3 车站分时段上车人数

在此基础上，计算各车站在控制时间段内的平均控流率，如图2．控流率越大，表示客流需求与列车运输承载量之间的矛盾越突出．由图2可见，前方车站中D站控流强度较大，平均控流率为43.7%，达到一个小峰值；其后J站控流强度最大，控流率为55.8%，一方面由于J站本身到达客流较大，另一方面由于前方车站客流较大，列车到达J站时剩余承载能力极其有限．此外，从各站乘客平均等待周期来看，不采用限流控制时，A至F站无需额外侯乘，G站自07∶40起即第2个分时段开始产生滞留乘客，而H至J站在控制时段内乘客大量留乘，自第2个分时段起到达客流需要等待额外5个周期，这种情况随时间推移将更加严重，造成全线各站乘客候车周期严重不平衡；实施车站协同限流以后，B站至F站由于流量控制需额外候车，候车时间一般为3个周期，而G至J站乘客候车时间则可大幅优化，乘客可在等待约4个周期后离去，各站乘客候车时间趋于均衡，缓解部分大客流站乘客长时间滞留问题，协同限流后的各站平均等待周期如图3．

图2 车站平均控流率Fig.2 Average control flow rate at each station

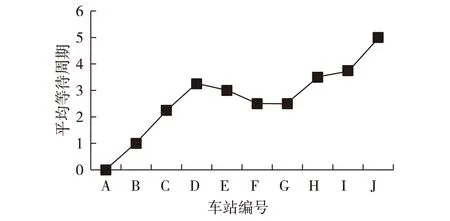
图3 各车站平均等待周期Fig.3 Average waiting period at each station

协同限流前后各车站滞留人数如图4，图4中限流协调控制条件下为整个控制时间段内(07∶30—08∶30)平均滞留人数，客流基本处于稳定状态；而无控制条件下，则在08∶00时各站台滞留人数达到控制时段内最高值．由图4两种情况对比可知，基于多站协同限流措施，通过控制B至E站乘客上车人数，预留后续相关车站的列车载客空间，可将乘客候车时间均衡化，由此降低局部车站过度拥挤带来的安全隐患，极大的缓解了后方车站的滞留现象．

图4 车站滞留人次比较Fig.4 Comparison of the total number of stranded passengers at each station

结 语

本研究考虑列车周期性运行特性，简化乘客的到达规律，使构建求解模型及算法简便有效，所提出限流措施主要面向车站客运组织，通过算例分析表明，该方法能从线路大客流均衡管控的角度，一定程度上有效缓解运能与运量之间的矛盾．然而本研究仍存在些许不足，首先，客流的基础数据可以通过预测模型更加精准拟合[15-18]；其次，单纯通过车站限流措施进行大客流疏散很难达到理想的效果，有必要结合加车、扣车、跳停、压缩运行时分及小交路折返等列车运行调整措施，实施站车协同管控，以实现网络及线路层车站和列车对客流的均衡集散[19-20]，最大程度减小对乘客出行和列车运行影响，提高服务乘客水平和列车正点率．

/

：

[1] 施云惠，熊梦伟，孙艳丰．城市轨道交通线网拥挤度指标体系研究[J]．铁道科学与工程学报，2016，13(11)：2290-2298． Shi Yunhui, XiongMengwei, SunYanfeng. Research on congestion degree index system of urban rail transit network [J]. Journal of Railway Science and Engineering, 2016,13(11):2290-2298.(in Chinese)

[2] 郑雪梅，蒋 熙．基于系统动力学的地铁客村站客流控制研究[J]．铁道科学与工程学报，2016，13(11)：2284-2289． Zheng Xuemei, Jiang Xi. The study of passenger flow control at kecun station of urban rail transit based on system dynamics[J].Journal of Railway Science and Engineering, 2016,13(11):2284-2289. (in Chinese)

[3] 肖慧雅，姚丽亚，曾 伟，等．城市轨道交通站点限流设施优化方法研究[J]．道路交通与安全， 2016，16(6)：46-50． Xiao Huiya, Yao Liya, Zeng Wei, et al. Study of the optimization methods of flow-limiting facilities in urban rail transit stations [J]. Road Traffic & Safety, 2016,16(6):46-50.(in Chinese)

[4] 李冰玉，秦孝敏．城市轨道交通网络大客流拥堵传播机理研究[J]．中国安全科学学报，2016，26(1)：162-168． Li Bingyu, Qin Xiaomin. Study on propagation mechanism of mass passenger flow congestion in urban rail transit network[J]. China Safety Science Journal, 2016, 26(1):162-168.(in Chinese)

[5] 曹志超，袁振洲，张思林，等．城市轨道交通大客流等车时间计算模型[J]．铁道标准设计，2015, 59(3)：33-37． Cao Zhichao, Yuan Zhenzhou, Zhang Silin, et al. The model of calculating waiting time in urban rail transit under oversaturated conditions [J]. Railway Standard Design, 2015, 59(3):33-37.(in Chinese)

[6] 张 正，蒋 熙，贺英松．城市轨道交通高峰时段车站协同限流安全控制研究[J]．中国安全生产科学技术，2013，9(10)：5-9． Zhang Zheng, Jiang Xi, He Yingsong. Study on collaborative flow-limiting safety control of urban railway station in peak hours[J]. Journal of Safety Science and Technology, 2013, 9(10):5-9. (in Chinese)

[7] 赵 鹏，姚向明，禹丹丹．高峰时段城市轨道交通线路客流协调控制[J]．同济大学学报自然科学版，2014，42(9)：1340-1346． Zhao Peng, Yao Xiangming, Yu Dandan. Cooperative passenger inflow control of urban mass transit in peak hours [J]. Journal of Tongji University Natural Science,2014,42(9):1340-1346.(in Chinese)

[8] Li Wei, Xu Ruihua, Luo Qin, et al. Coordination of last train transfers using automated fare collection (AFC) system data [J]. Journal of Advanced Transportation, 2017, 50(8): 2209-2225.

[9] Zhang Jianhua,Zhao Mingwei,Liu Haikuan, et al. Networked characteristics of the urban rail transit networks[J]. Physica A: Statistical Mechanics and its Applications, 2012, 392(6): 1538-1546.

[10] 邱 蓉. 地铁平行换乘车站旅客行为及运能分析[J].铁道标准设计. 2013(4): 8-13. Qiu Rong. Analysis on passenger behavior and transport capacity[J]. Railway Standard Design, 2013(4): 8-13.(in Chinese)

[11] 陈伽申,蒲 琪,涂颖菲. 城市轨道交通乘客上下车行为与停站时间研究[J]. 城市轨道交通研究,2017(1):61-64, 78. Chen Jiashen, Pu Qi, Tu Yingfei. On the relation between passenger boarding behavior and train dwelling time[J]. Urban Mass Transit, 2017(1):61-64, 78.(in Chinese)

[12] 李凌燕. 城市轨道交通网络突发大客流传播机理及组织优化[D].成都: 西南交通大学，2015. Li Lingyan. Sudden passenger flow propagation mechanism analysis and organizational optimization in urban rail transit network[D]. Chengdu: Southwest Jiaotong University, 2015.(in Chinese)

[13] 李 曼,王艳辉,晋 君,等. 基于路网客流模态的城市轨道交通网络拥堵演变机理[J]. 东南大学学报自然科学版，2017，47(2):404-409. Li Man, Wang Yanhui, Jin Jun, et al. Network congestion evolution law of urban rail transit based on network passenger flow model[J]. Journal of Southeast University Natural Science Edition, 2017, 47(2):404-409.(in Chinese)

[14] Niu Huimin,Zhou Xuesong. Optimizing urban rail timetable under time-dependent demand and oversaturated conditions[J]. Transportation Research Part C,2013, 36(11): 212-230.

[15] 王玉萍. 城市轨道交通客流预测与分析方法[D].西安：长安大学,2011. Wang Yuping. Study on urban rail transit passenger forecast and analysis [D]. Xi’an: Chang’an University, 2011.(in Chinese)

[16] 郭 平. 城市轨道交通客流特征及预测相关问题[J]. 城市轨道交通研究,2010(1):58-62. Guo Ping. On characteristics and prediction of urban rail transit passenger flow[J].Urban Mass Transit,2010(1):58-62.(in Chinese)

[17] 朱广宇,王雨晨,张 彭, 等.基于变点发掘的城市轨道交通客流预测模型[J].中南大学学报自然科学版,2016,47(6):2153-2159. Zhu Guangyu, Wang Yuchen, Zhang Peng, et al. A forecasting model for urban rail transit passenger flow based on change-point detection method[J]. Journal of Central South UniversityScience and Technology, 2016, 47(6): 2153-2159.(in Chinese)

[18] 石庄彬,张 宁,邵星杰, 等.城市轨道交通客流高峰持续时间预测方法[J].城市轨道交通研究,2016,19(7):35-39. Shi Zhuangbin, Zhang Ning, Shao Xingjie, et al. Prediction of passenger flow duration in urban rail transit peak hours[J]. Urban Mass Transit,2016, 19(7): 35-39.(in Chinese)

[19] 张 璐.基于动态客流的城市轨道交通网络列车时刻表优化研究[D].北京：北京交通大学,2016. Zhang Lu. Timetable optimization of urban rail transit network based on dynamic passenger flow[D]. Beijing：Beijing Jiaotong University, 2016.(in Chinese)

[20] 罗 钦,杨永泰,莫义弘,等. 城市轨道交通行车调度应急辅助决策系统的设计与实现[J]. 铁道运输与经济,2017, 39(2):85-89. Luo Qin, Yang Yongtai, Mo Yihong, et al. Design and realization of emergency auxiliary decision-making system of traffic control for urban rail transit[J].Railway Transport and Economy, 2017, 39(2):85-89.(in Chinese)

【中文责编：方圆；英文责编：木南，淡紫】

Modelingofflowco-controlamongmulti-stationsbasedonpassengerequilibriumwaitingforurbanrailtransit

MaYu1,WangZhuoqun2,WenShaobiao1,andLuoQin2,3

1)PassengerTransportNo.1Company,OperationHeadquartersofShenzhenMetroGroupCo.Ltd.,Shenzhen518071,GuangdongProvince,P.R.China2)CollegeofUrbanRailTransit,ShenzhenUniversity,Shenzhen518060,GuangdongProvince,P.R.China3)CollegeofUrbanTrafficandLogistics,ShenzhenTechnologyUniversity,Shenzhen518118,GuangdongProvince,P.R.China

Mass passenger flow in urban rail transit always presents non-balanced, non-steady and non-linear feature. Flow control becomes the main process in passenger organization management since it would directly influence the passenger service level and train operation reliability. According to the train periodic running characteristics and simplifying the arrival of passengers in accordance with the law of uniformity based on analyzing delay influence of passenger waiting time under the condition of mass passenger flow, this paper presents co-passenger flow control model among multi-stations in a single line, aiming to balance the passengers’ waiting time in each station. The fmincon function provided by Matlab is used to find the optimal value. The result analysis of a simulation case shows that the model is effective and reasonable to alleviate the contradiction between transport capacity and traffic volume from the angle of equal control of mass passenger flow and to avoid some stations of the line having large number of stranded passengers.

urban rail transit; mass passenger flow; waiting time equalization; multi-stations coordination; flow control; trip experience

2017-03-29；Accepted：2017-06-08

Associate professor Luo Qin．E-mail: luoqin@szu.edu.cn

U 29-39；TP 39

：Adoi：10.3724/SP.J.1249.2017.05537

Foundation：Research Projects of the Social Science and Humanity on Young Fund of the Ministry of Education (15YJCZH108)

：Ma Yu，Wang Zhuoqun, Wen Shaobiao, et al. Modeling of flow co-control among multi-stations based on passenger equilibrium waiting for urban rail transit[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(5): 537-543.(in Chinese)

教育部人文社会科学研究青年基金资助项目(15YJCZH 108)

马 羽(1972—)，男，深圳市地铁集团有限公司工程师．研究方向：轨道交通运营管理．E-mail：00278@szmcob.com

引文：马 羽，王卓群，温少表，等．基于乘客均衡候车的城市轨道交通协同限流建模[J]. 深圳大学学报理工版，2017，34(5)：537-543.