分数阶模拟电容和模拟电感的设计

何清平，刘佐濂，杨 汝

广州大学物理与电子工程学院，广东广州 510006

【物理与应用物理/PhysicsandAppliedPhysics】

分数阶模拟电容和模拟电感的设计

何清平，刘佐濂，杨 汝

广州大学物理与电子工程学院，广东广州 510006

基于波特图频域近似算法和阻容分抗电路设计出分数阶模拟电容，利用广义阻抗变换电路把α(0<α<1)阶模拟电容转换为α阶模拟电感，把分数阶模拟电容的阶次扩展至0～2阶．采用Multisim软件对分数阶模拟电感、分数阶LC串联电路仿真，结果与理论分析基本一致．

电子电路；分数阶电路；LC串联电路；模拟电感；模拟电容；阻抗变换

长期以来，电容和电感被公认是基于整数阶微积分建立电路分析的．然而，大量研究表明，电容和电感本质上是分数阶的，基于分数阶微积分建立电容和电感的数学模型更能准确反映实际电容和电感的电学特性[1-4]．Westerlund等[2]通过实验测定出不同电介质下分数阶电容的阶数；Jesus等[3]已制造出具有0.59和0.42阶的分数阶电容；Machado等[4]指出基于趋肤效应可制造出任意阶次的电感元件．王发强等[5-6]使用阻容分抗电路设计出分数阶模拟电容，用于分数阶Lorenz、Chen、Liu和多翼等混沌系统的电路实现[7-11]，进一步证实电路系统的分数阶特性．分数阶LC串并联电路[12-13]、LCL型电路[14]和滤波电路[15-16]均已有系统的理论研究．本研究在缺乏分数阶元件的情况下，基于频域近似算法和阻容分抗电路，设计0～2阶的分数阶模拟电容和模拟电感，可为研究分数阶电路特性，拓展分数阶电路的工程应用提供替代元件．

1 分数阶微积分的基本理论

1.1分数阶微积分的定义

分数阶微积分是研究任意阶次微分、积分算子的特性及应用的数学分析方法[17]．其中，Caputo定义的分数阶微积分，其初值条件是整数阶的，具有清晰的物理意义，常用于解决工程应用和物理问题．

Caputo积分的定义式[17]为

(1)

Caputo微分的定义式[17]为

(2)

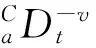
Caputo微积分定义的Laplace变换为[17]

(3)

(4)

其中，L[·]为拉普拉斯变换；s为复频率；F[s]是变量为s的函数；k≥0且为整数，n=⎣α」+1．

式(3)和式(4)表明，Caputo定义的微积分的Laplace变换简单，只需得到函数f(t)的整数阶导数的初值(f(k)(0),k=0,1, …，n-1)即可，极大地降低了分数阶微积分方程的求解难度，更具工程实用性．

1.2分数阶微积分的频域近似算法

分数阶微积分运算的求解，工程上常用波特图频域近似算法[18-19]，先对分数阶微积分进行时域-频域转换，再在频域中应用分段线近似法进行计算．由式(3)可知，阶次为α(0<α<1)的分数阶积分的传递函数为H(s)=1/sα， 用单极点分数幂表示为H(s)=1/(1+s/pT)α， 其波特图为一条斜率为-20αdB/dec的直线．如图1，在工程计算中，通常用斜率为0和-20dB的线段组成的锯齿线来近似，把分数阶函数转化为求解系统的零极点对的问题[18]．

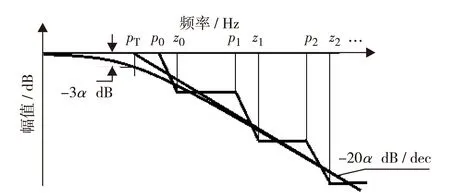
图1 1/(1+s/pT)α的波特图及其锯齿线逼近[18]Fig.1 Bode plot of 1/(1+s/pT)α and its approximation with zigzag straight lines[18]

假设最大角频率为ωmax的频率范围内，工程实际所要求动力学系统变量的计算误差不超过y(y为正值，单位：dB)，工作频段限制为N个，取0<α<1， 则1/sα的近似传递函数[19]为

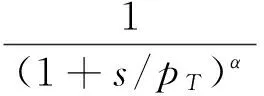
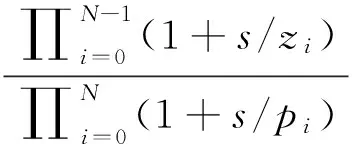
(5)

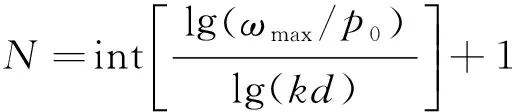
2 分数阶模拟电容和模拟电感的设计

2.1α(0<α<1)阶模拟电容的设计

分数阶模拟电容可采用树型、链型和混合型的阻容分抗电路进行模拟[6]．在复频域中，电容量为C0、 阶次为α的分数阶电容的传递函数为F(s)=1/(C0sα)． 对链型阻容分抗电路，其两端之间的复频域表达式为[6]

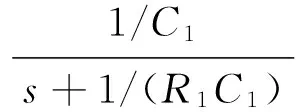
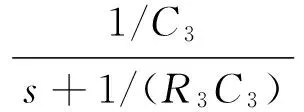
(6)

根据工程需求，选定α、ωmax、pT和y的值并代入式(5)计算，得到分数阶传递函数H(s)=1/sα(α=0.1～0.9)的频域近似表达式．设分数阶模拟电容的值为C0、 阶次为α， 对比式(5)和式(6)的参数，计算得R1,R2, …,Rn和C1,C2, …,Cn的值．

2.2分数阶模拟电感的设计及阶次扩展

图2是由运算放大器组成的一种广义阻抗变换器(generalimpedanceconverter,GIC)电路[20]，它既能模拟电容，也能模拟电感，电路所呈现的阻抗性质由Z1～Z4及ZL所选择的电容或电阻来决定．

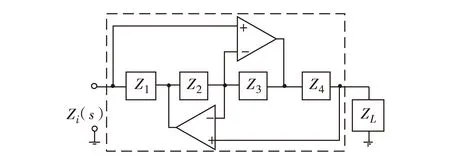
图2 一种GIC电路[20]Fig.2 A general impedance converter circuit[20]

若运算放大器是理想的，则该电路输入阻抗为

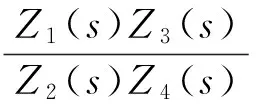
(7)

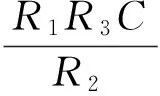
3 仿真验证

3.1β(0<β<1)阶模拟接地电感的设计

根据式(7)和图2的GIC电路，可把β阶的分数阶电容回转为β阶的模拟接地电感．图3是基于运放LF351D设计的GIC电路，取R1=R2=R3=RL=1kΩ，C4为β阶电容量为1μF的分数阶电容，可得到β阶电感量为1H的模拟接地电感，取不同的电阻值可得到不同的模拟电感值．分数阶电容C4采用文献[8]的参数ωmax=100rad/s、pT=0.01rad/s、y=2dB，由式(5)和式(6)计算出β阶次、电容值为1μF时链型分抗电路的阻容元件参数．

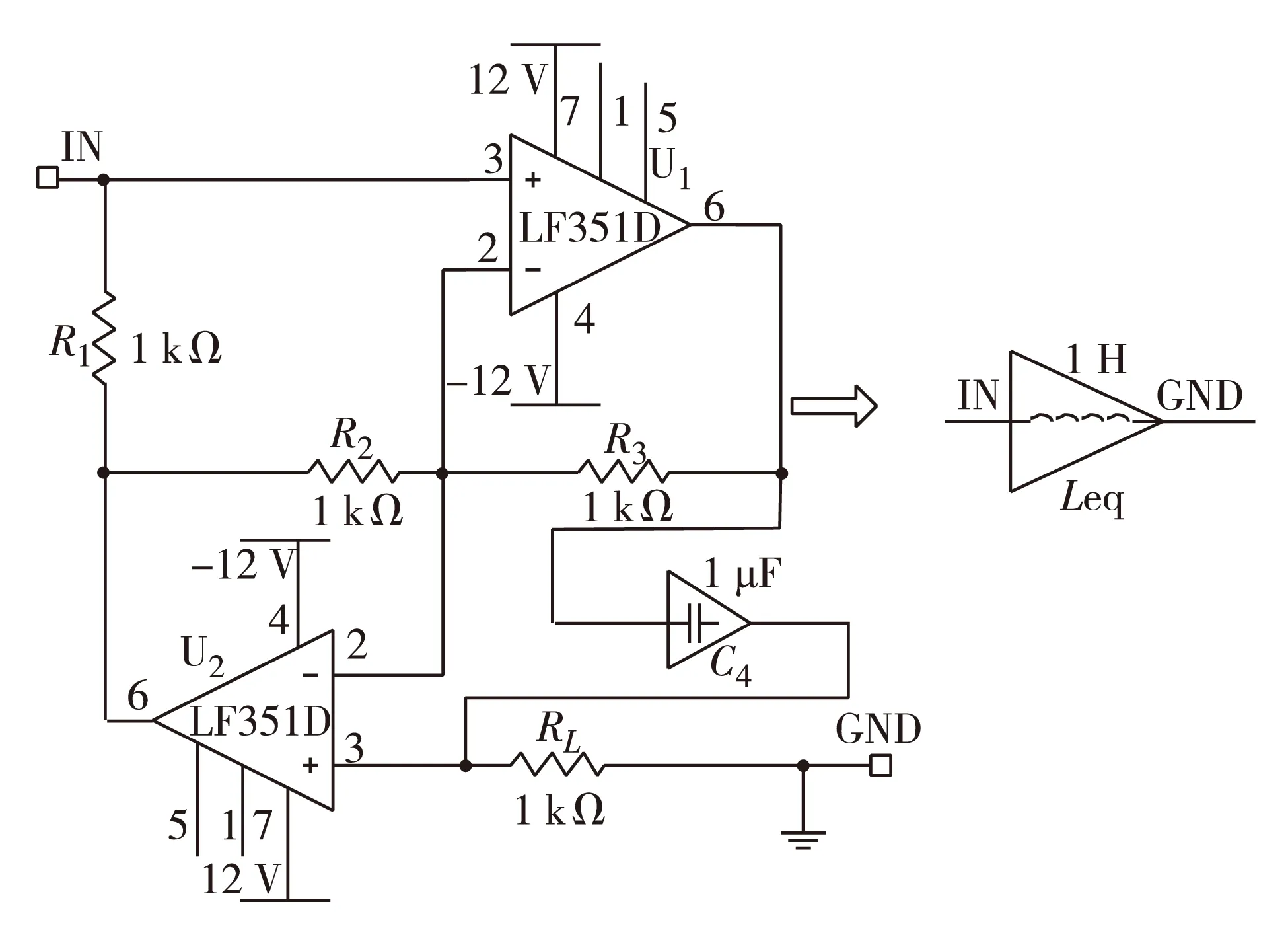
图3 β阶电容回转为β阶电感的GIC电路Fig.3 A GIC circuit to transform β-order capacitor into β-order inductor

3.2β阶模拟接地电感的仿真验证

用正弦电压ui=sin(wt)激励时，流过β阶电感的电流相位比电压超前βπ/2． 用Multisim软件对图3的电路进行仿真，得到β阶模拟接地电感的正弦电压激励的电流波形，在虚拟示波器上显示的波形如图4．波形①为电感两端的电压波形，波形②、③和④分别对应阶次β为0.4、0.8和1.0，电感值为1H时的电感电流，电压和电流的转换关系为每500mV表示1mA．可见，电感电流与电压的相位关系与理论分析基本一致．

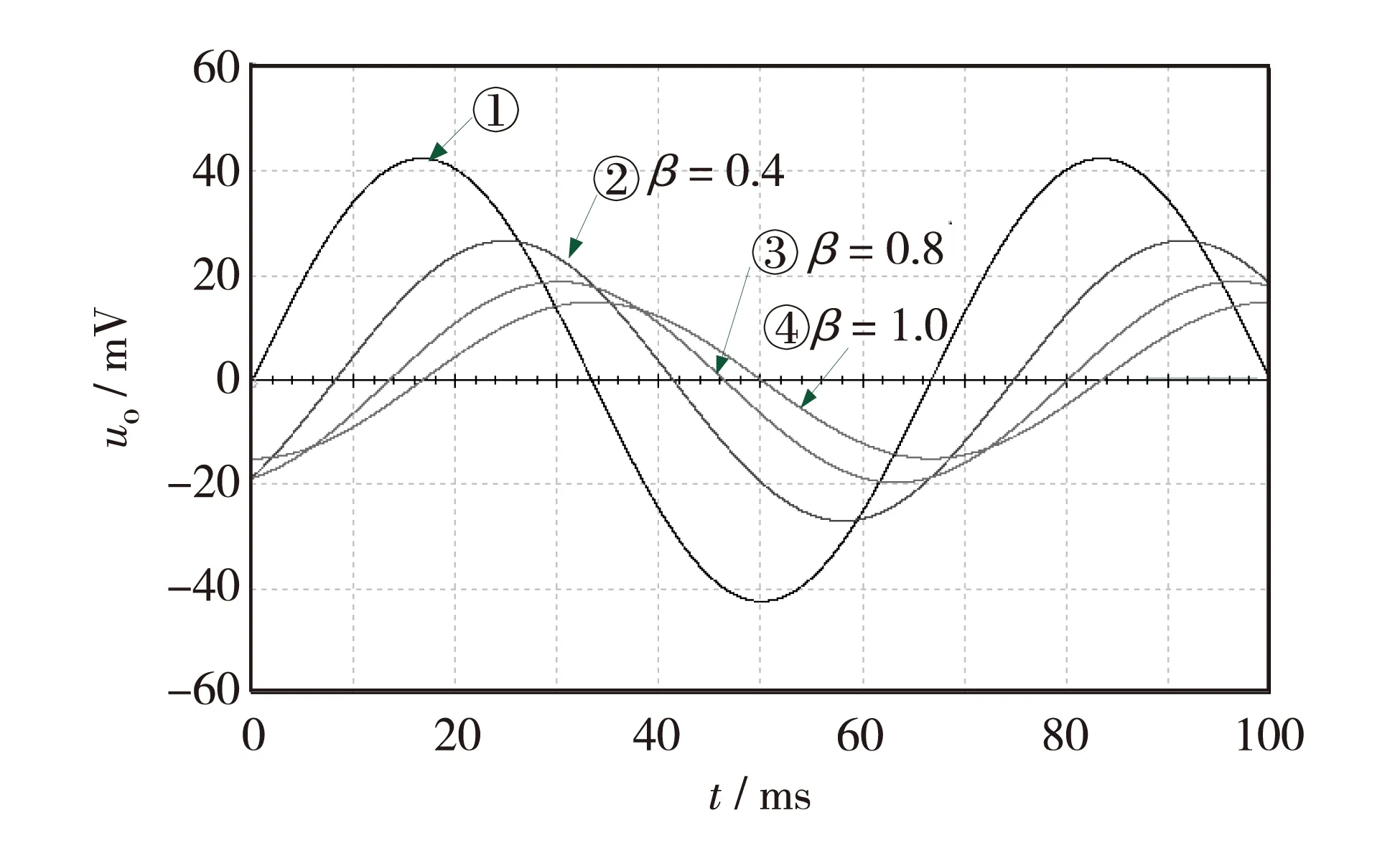
图4 分数阶电感的正弦电压激励响应①量程为20 mV/Div; ② 量程比①放大250倍；③量程比①放大100倍；④ 量程比①放大50倍Fig.4 The sine wave response of the fractional order inductor

3.3LβCα串联电路仿真

为验证所设计分数阶模拟电容和模拟电感的正确性，对分数阶LβCα串联电路进行仿真．使用Multisim分析自带的波特仪对串联电路的幅频特性，得到分数阶串联电路的谐振频率，再与理论计算得到的谐振频率ωres对比．ωres的计算公式为[12]

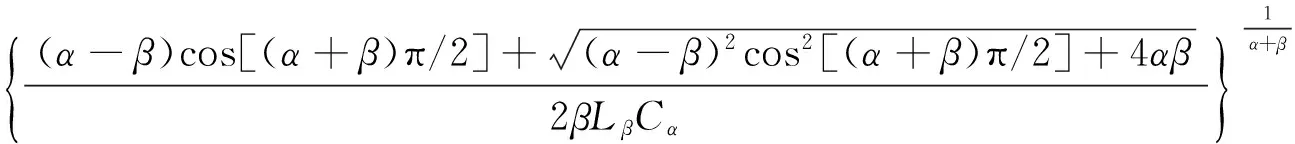
(8)

选取分数阶模拟电容和模拟电感的谐振参数时，应确保谐振频率位于其正常工作频域内．由式(8)可得，当α=0.4，β=0.8，Cα=1μF，Lβ=5kH时，fres=ωres/(2π)=10.80Hz，与图5(a)仿真得到的谐振频率基本一致；当α=0.8，β=0.4，Cα=1μF，Lβ=6kH时，fres=ωres/(2π)=13.78Hz，与图5(b)中仿真得到的谐振频率基本一致．可见，电路仿真得到的谐振频率与理论计算得到的基本一致，证明所设计的分数阶模拟电容和模拟电感有效可行．

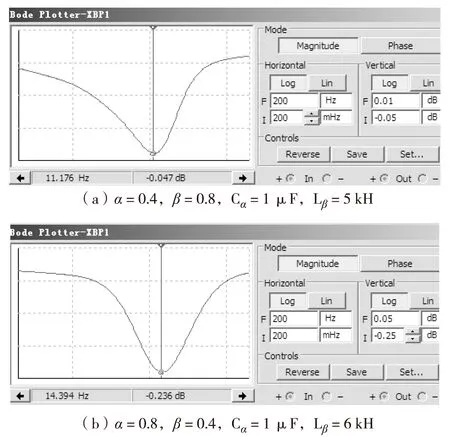
图5 分数阶LβCα串联电路仿真的波特图Fig.5 Simulation Bode plot of fractional order LβCα serial circuit

结 语

基于分数阶微积分的基本概念，总结了频域近似算法的基本原理，将其与链型阻容分抗电路的传递函数进行对比，得到分数阶模拟电容的等效电路参数，设计出α(0<α<1)阶的模拟电容；利用GIC电路，把α阶的模拟电容转换为α阶的模拟电感，把分数阶模拟电容的阶次扩展至0～2阶．为验证设计的正确性，采用Multisim软件对阶次为0～1的分数阶模拟电感进行仿真，通过比较电感电压和电感电流的相位关系，验证了分数阶电感的正确性；同时，对分数阶LC串联电路仿真得到的谐振频率与理论计算结果基本一致，进一步验证了分数阶模拟电容和模拟电感设计的正确性．所设计的分数阶模拟电容和模拟电感可用于分数阶混沌电路、滤波电路和谐振电路等场合，为研究分数阶电路的工程应用提供参考．

/

：

[1] 王发强，马西奎．电感电流连续模式下 Boost 变换器的分数阶建模与仿真分析[J]．物理学报，2011，60(7)：89-96． Wang Faqiang, Ma Xikui. Fractional order modeling and simulation analysis of Boost converter in continuous conduction mode operation[J]. Acta Physica Sinica,2011,60(7):89-96.(in Chinese)

[2] Westerlund S, Ekstam L. Capacitor theory[J]. IEEE Transactions on Dielectrics and Electrical Insulation,1994,1(5):826-839.

[3] Jesus I S, Machado J A T. Development of fractional order capacitors based on electrolyte processes[J]. Nonlinear Dynamics,2009,56(1):45-55.

[4] Machado J A T, Galhano A M S F. Fractional order inductive phenomena based on the skin effect[J]. Nonlinear Dynamics,2011,68(1/2):107-115.

[5] 王发强，刘崇新．分数阶临界混沌系统及电路实验的研究[J]．物理学报，2006，55(8)：3922-3927． Wang Faqiang, Liu Chongxin. Study on the critical chaotic system with fractional order and circuit experiment[J]. Acta Physica Sinica,2006,55(8):3922-3927.(in Chinese)

[6] 刘崇新．分数阶混沌电路理论及应用[M]．西安:西安交通大学出版社，2011：118-128． Liu Chongxin. Theory and application of Fractional order chaotic circuit[M]. Xi’an: Xi’an Jiaotong University Press,2011:118-128.(in Chinese)

[7] 贾红艳，陈增强，薛 薇．分数阶Lorenz系统的分析及电路实现[J]．物理学报，2013，62(14)：140503． Jia Hongyan, Chen Zengqiang, Xue Wei. Analysis and circuit implementation for the fractional order Lorenz system[J]. Acta Physica Sinica,2013,62(14):140503.(in Chinese)

[8] 陈 恒，雷腾飞，王 震，等．分数阶Chen混沌系统的动力学分析与电路实现[J]．河北师范大学学报自然科学版，2015，39(3)：208-215． Chen Heng, Lei Tengfei, Wang Zhen, et al. Dynamics analysis and circuit implementation for the fractional order Chen chaotic system[J]. Journal of Hebei Normal University Natural Science Edition,2015,39(3):208-215.(in Chinese)

[9] 陈向荣，刘崇新，王发强，等．分数阶Liu混沌系统及其电路实验的研究与控制[J]．物理学报，2008，57(3)：1416-1422． Chen Xiangrong, Liu Chongxin, Wang Faqiang, et al. Study on the fractional order Liu chaotic system with circuit experiment and its control[J]. Acta Physica Sinica,2008,57(3):1416-1422.(in Chinese)

[10] 杨志宏，张彩霞，屈双惠，等．异分数阶 chen 系统的动力学特性及其多元电路实现[J]．江西师范大学学报自然科学版，2017，41(2)：133-139． Yang Zhihong, Zhang Caixia, Qu Shuanghui, et al. The dynamic properties of the heterogeneous fractional order Chen system and its plural circuit implementation[J]. Journal of Jiangxi Normal University Natural Science,2017,41(2):133-139. (in Chinese)

[11] 贾红艳，王庆合．异结构分数阶四翼混沌系统的同步及电路实现[J]. 天津科技大学学报，2017,32(1):62-67． Jia Hongyan，Wang Qinghe．Synchronization of four-wing fractional-order chaotic system with different structures and its circuit implementation[J]. Journal of Tianjin University of Science & Technology,2017,32(1):62-67.(in Chinese)

[12] Radwan A G, Salama K N. Passive and active elements using fractional circuit[J]. IEEE Transactions on Circuit and Systems,2011,58(10):2388-2397.

[13] 刁利杰，张小飞，陈帝伊．分数阶并联RLαCβ电路[J]．物理学报，2014，63(3)：038401． Diao Lijie, Zhang Xiaofei, Chen Diyi. Fractional-order multipleRLαCβcircuit[J]. Acta Physica Sinica,2014,63(3):038401.(in Chinese)

[14] 余战波．分数阶T型LαCβ电路仿真研究[J]．西南大学学报自然科学版，2015，37(2)：141-147． Yu Zhanbo. Numerical simulation of a T-shaped fractionalLαCβcircuit[J]. Journal of Southwest University Natural Science Edition,2015,37(2):141-147.(in Chinese)

[15] Zhou Rui，Zhang Runfan，Chen Diyi. Fractional-order LβCα low-pass filter circuit[J]. Journal of Electrical Engineering & Technology,2015,10(4):1598-1610.

[16] Ahmadi P , Maundy B , Elwakil A S , et al. High-quality factor asymmetric-slope band-pass filters: a fractional-order capacitor approach[J]. IET Circuits Devices & Systems,2012,6(3):187-197.

[17] Podlubny I. Fractional differential equations[M]. New York, USA: Academic Press,1999:79-106

[18] Charef A, Sun H H, Tsao Y Y, et al. Fractal system as represented by singularity function[J]. IEEE Transactions on Automatic Control,1992,37(9):1465-1470.

[19] Ahmad W M, Sprott J C. Chaos in fractional-order autonomous nonlinear systems[J]. Chaos Solitons & Fractals,2003,16(2):339-351.

[20] 燕奎臣，王晓辉，李 硕．回转器及其应用[J]．仪表技术与传感器，2000(5)：36-39． Yan Kuichen, Wang Xiaohui, Li Shuo. Gyrator and its application[J]. Journal of Instrument Technique and Sensor,2000(5):36-39.(in Chinese)

【中文责编：英子；英文责编：子兰】

Designofsimulatorforfractionalordercapacitorandinductor

HeQingping,LiuZuolian,andYangRu

SchoolofPhysicsandElectronicEngineering,GuangzhouUniversity,Guangzhou510006,GuangdongProvince,P.R.China

A fractional order simulant capacitor is designed based on the Potter frequency domain approximation algorithm and the impedance capacitance division circuit.By using a generalized impedance transformation circuit, theα(0<α<1) order simulant capacitor is converted to anαorder simulant inductor. The order of the fractional order simulant capacitor is extended from zero to second. The fractional order simulant inductance and fractional order LC series circuit are simulated by using Multisim software, and the results are in good agreement with the theoretical analysis ones.

electronic circuit; fractional order circuit; LC serial circuit; inductive simulator; capacitive simulator; impedance conversion

2017-01-06；Accepted：2017-05-21

Professor Yang Ru. E-mail: yangru@gzhu.edu.cn

TN 721.2

：Adoi：10.3724/SP.J.1249.2017.05516

Foundation：National Natural Science Foundation of China (51277035)；Natural Science Foundation of Guangdong Province (2014A030313528)

：He Qingping, Liu Zuolian, Yang Ru. Design of simulator for fractional order capacitor and inductor[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(5): 516-520.(in Chinese)

国家自然科学基金资助项目(51277035)；广东省自然科学基金资助项目(2014A030313528)

何清平(1978—)，男，广州大学实验师．研究方向：非线性电路理论及应用．E-mail:jerryhqp@126.com

引文：何清平，刘佐濂，杨 汝．分数阶模拟电容和模拟电感的设计[J]. 深圳大学学报理工版，2017，34(5)：516-520.