基于索梁活载比的部分斜拉桥布索形式比较

彭晶蓉，贺拴海，李 尧

1) 长安大学公路学院，陕西西安710064；2)中交第一公路勘察设计研究院有限公司，陕西西安710064

【土木建筑工程/ArchitectureandCivilEngineering】

基于索梁活载比的部分斜拉桥布索形式比较

彭晶蓉1，贺拴海1，李 尧2

1) 长安大学公路学院，陕西西安710064；2)中交第一公路勘察设计研究院有限公司，陕西西安710064

推导部分斜拉桥刚构体系索梁活载比简化计算公式，对不同的布索方式提出了用索量的概念．部分斜拉桥结构的斜拉索与主梁夹角越大(≤54.74°)时，斜拉索分担的竖向荷载较大，故辐射形布索方式的索梁活载比最大，扇形次之，竖琴形布置最小；而对应的斜拉索的总长度辐射形最长，扇形次之，竖琴形最短．可推断，在结构设计尺寸初步确定的情况下，以用索量为目标可挑选出最为经济的布索方式．以某部分斜拉桥为工程背景，建立3种布索形式的有限元计算模型，结果表明，为达到预期的索梁活载比，辐射形布索方式用索量最少；扇形次之，比辐射形多25%；竖琴形最多，比辐射形多81%．有限元结果与简化计算公式结果规律一致，数值仅差8%．

桥梁工程；部分斜拉桥；布索方式；辐射形；扇形；竖琴形；索梁活载比；用索量

部分斜拉桥起源于瑞士，近年来，在世界各地得到广泛的应用．目前国外已建及在建部分斜拉桥已有百余座[1-3]．中国起步较晚，2000年建成的芜湖长江大桥(180m+312m+l80m)是目前为止世界上跨度最大的部分斜拉桥[4]．作为刚构桥与斜拉桥的组合结构，部分斜拉桥的力学行为介于两者之间，由梁的受弯、受压以及索的受拉共同承受竖向荷载．其刚柔相济、经济美观及施工方便等特点使得部分斜拉桥近年来迅速发展[5-7]．

部分斜拉桥的拉索是其重要组成部分，拉索的布置形式也是影响结构性能的重要参数，不同的布索形式在主梁上的分布区域不同，斜拉索与主梁、主塔的夹角也不同，使得结构的受力行为也相差甚远[8-10]．文献[11]介绍了部分斜拉桥是介于连续梁桥与斜拉桥之间的新型桥梁，它的力学行为介于两者之间；通过调整斜拉索的布置形式，计算了荷载作用下主梁的弯矩和轴力在塔根附近弯矩值的变化，结果表明：部分斜拉桥的布索方式将直接影响主梁的受力，且密索布置优于稀疏索布置，但其优势不明显，从布索方式上看，辐射式明显优于竖琴式和扇形．文献[12]分析各种斜拉索布索形式下曲线矮塔斜拉桥动力性能研究，通过比较扇形与竖琴形两种布索形式的频率结果，表明竖琴形布索受索力方向的影响，使全桥刚度略微下降．

本研究基于部分斜拉桥索、梁共同承担活荷载的受力特点，在推导设计参数索梁活载比简化计算公式的基础上，提出了用索量，在结构的初步设计尺寸确定的情况下，比较不同的布索方式的优劣．

1 部分斜拉桥的布索方式及特点

常规斜拉桥设计中最为常见的索面布置分为辐射形、扇形和竖琴形3种，如图1．辐射形布置是塔上锚固集中于塔顶一点，主梁锚固点等距布置．这种布索方式斜拉索与主梁夹角较大，塔上仅设一个索鞍．塔顶与斜拉索的锚固位置为全封闭整体节点，节点处所有附连件都在节点处焊连，使得该处焊缝密集，纵横交叉，受力复杂，且在维修、养护上比较困难．竖琴形布置的斜拉索与主梁的夹角相同，简洁美观；塔上各锚固点的间距大，对索塔的受力有利；且各锚点结构形式相同，方便施工．而扇形布置介于辐射形和竖琴形之间，塔上各锚固点的间距适中[13-15]．

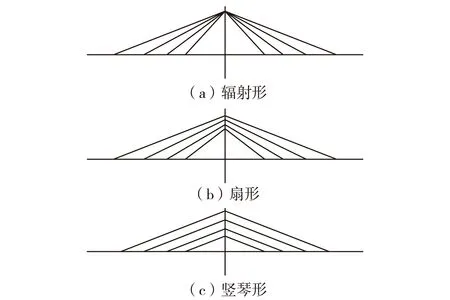
图1 斜拉桥索面立面布置形式Fig.1 Different layouts of cables for cable stayed bridge

根据目前统计的国内外部分斜拉桥资料可见，部分斜拉桥的索面立面布置形式主要为扇形和竖琴形[12，16-20]．鉴于部分斜拉桥各种布索方式的拉索倾角变化是结构受力的主要因素，本研究结合经济指标与索梁活载比对布索方式进行研究．

2 公式推导

2.1索梁活载比

所谓部分斜拉桥，是因为它外观上既有塔又有斜拉索，外形类似斜拉桥，但在结构性能上，斜拉索仅分担部分荷载，还有相当部分的荷载由梁的受弯、受剪来承担．根据文献[20-24]提出的部分斜拉桥索梁活载比η的概念，认为部分斜拉桥在活荷载作用下，斜拉索和主梁各自承担活载的比值定义为索梁活载比．索梁活载比取决于结构参数，即桥梁结构的几何尺寸、物理材料性质等，故一座桥梁结构存在唯一的索梁活载比与之对应．

按照比拟梁的思想，遵循结构力学的基本假设，以一座三跨刚构体系的部分斜拉桥为例，推导索梁活载比的计算公式．简化示意图如图2．

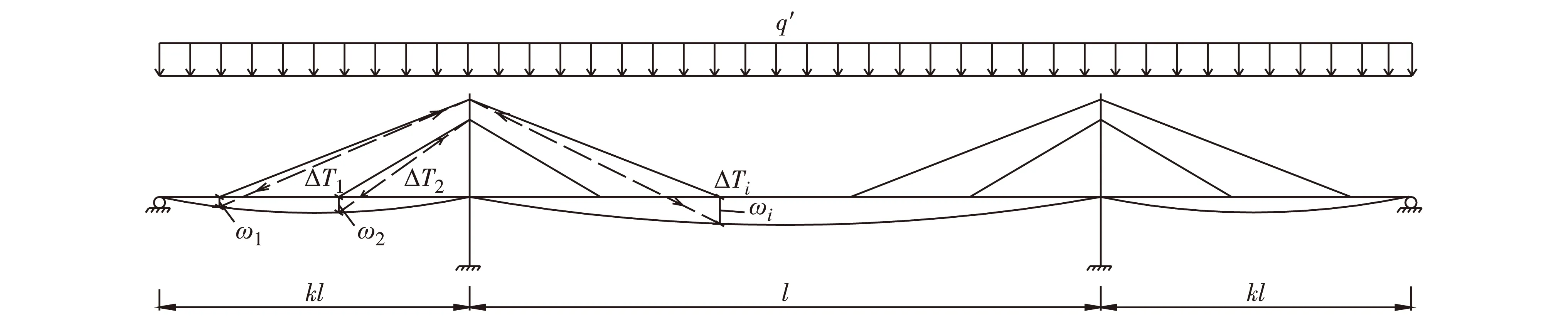
图2 部分斜拉桥示意图Fig.2 Diagram of extra-dosed bridge

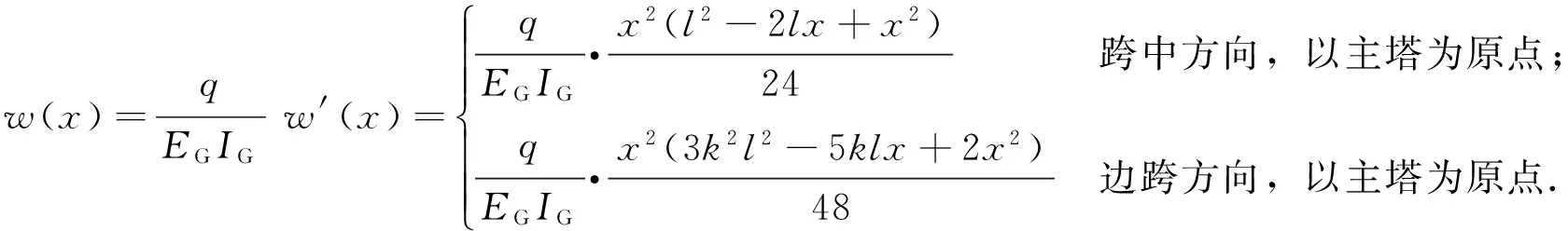
(1)

假设拉索i在主梁上锚固点的挠度为ω(xi)， 根据材料力学公式ΔTi/(EciAci)=Δli/Lci, 可得主梁上施加集度为q′的均布荷载时，结构索梁活载比为

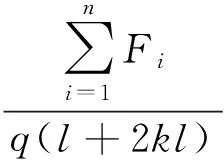
(2)

其中，Eci、Aci、Lci、 Δli、αi和xi分别为第i根索的弹性模量、拉索横截面面积、拉索长度、拉索变形量、拉索与主梁的夹角(锐角)、拉索主梁锚固点与塔底的距离．一般桥梁设计中拉索材料及拉索面积相同，则式(2)可简化为

(3)

2.2全桥用索量

对于桥梁结构几何尺寸及拉索材料均确定的情况，由式(2)可知其索梁活载比η与拉索倾角α有直接关系．为比较部分斜拉桥的3种布索方式对结构性能的影响，假定条件如下：一是结构的跨径布置相同，且拉索在主梁上的锚固点相同；二是主塔塔高相同，且尾索在主塔上的锚固点相同．仅通过改变其它索在主塔上的锚固位置以达到不同的布索形式，如图3．

图3 布索方式示意图Fig.3 Diagram of different cable layouts

鉴于部分斜拉桥的3种拉索布置方式对应不同的斜拉索长度，现提出拉索用索量的概念Vc以对不同的布索方式进行评价．用索量Vc可表示为

(4)

其中，Vc为斜拉索的体积用量．由于Li=xi/cosαi，当每根斜拉索在主梁上的锚固点(xi)确定时，显然辐射形的斜拉索总长度最长、扇形其次、竖琴形最短．但由于索梁活载比η与拉索角度α相关，故需联立式(3)、(4)，才可得出拉索横断面面积Aci从而得到对应布索方式的用索量Vc．

3 工程实例分析

3.1工程概况

选取某部分斜拉桥为背景工程，该桥跨径为(108+208+108)m，主梁断面为变高度单箱双室直腹板箱梁，箱梁梁体中心线梁高3.8～6.0m(梁高按二次抛物线变化)．主梁上塔根无索区长25m，边支座无索区长12m，跨中无索区长30m，每一侧索面共布置9根拉索，则梁上锚固间距为8.0m，主塔塔顶锚固点距桥面28m．全桥示意图如图4，斜拉索为扇形布置时塔上锚固点间距为1.0m，对应的辐射形及竖琴形索面布置如图5．

图4 某部分斜拉桥扇形索面示意图(单位：m)Fig.4 Fan-shaped cables for an extra-dosed bridge (unit:m)

图5 辐射形及竖琴形索面示意图(单位：m)Fig.5 Radiation-shaped and harp-shaped cables for an extra-dosed bridge (unit: m)

当结构截面尺寸及跨径确定后，由式(3)可知主梁变形中间函数ω′(x)可根据索梁锚固点确定具体数值，已知主跨跨径l为208m，边跨跨径kl为108m，计算结果如表1．

3.2三种索面对比分析

表1 边、中跨主梁变形参数ω′(x)计算结果

表2 三种索面布置斜拉索倾角参数

表3 三种索面布置斜拉索长度参数

3.3有限元模型计算验证

以依托工程为背景建立有限元分析模型，模型主梁、主塔和桥墩均采用梁单元，斜拉索采用Ernst公式修正弹性模量的只受拉桁架单元．模型中结构的施工顺序及截面尺寸均保持一致，仅修改斜拉索索面的布置形式．

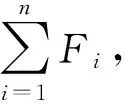
4 结 论

本研究推导简化计算公式，并以一座工程实例进行验算，得出以下结论：

1)根据部分斜拉桥的索梁活载比η的计算公式可知，斜拉索与主梁共同承担结构的活荷载，如若结构的尺寸初步确定，斜拉索的布置形式是该值的唯一影响因素．

2)依托工程计算结果表明，在跨径、塔高和截面形式等基本参数确定的情况下，辐射形布索方式的索梁活载比最大、扇形次之、竖琴形布置最小，其主要原因为斜拉索与主梁夹角较大时，分担的竖向荷载较多．但该结论并不绝对，对本研究中式(2)求偏导，可知最大的索梁活载比η对应的夹角α=54.74°． 因此，具体工程具体分析．

3)通过引入用索量Vc的概念，在初设阶段，可对3种布索方式的经济性、美观性、适用性以及施工难易程度等因素综合对比分析，对设计者而言有一定的参考价值．

4)由于部分斜拉桥的塔高较低，相比常规斜拉桥而言主塔截面尺寸较小．辐射形索面在施工时所有拉索均需锚固于塔顶，施工难度大，对锚固区要求高，本结论虽表明辐射形用索量最少，但缺少施工难度、 局部受力等综合因素的分析， 有待完善．

/

：

[1] 朱 刚.矮塔斜拉桥方案设计及分析研究[D].杭州：浙江大学，2008. Zhu Gang. Project design and analysis research of extra-dosed cable-stayed bridge [D].Hangzhou：Zhejiang University，2008.(in Chinese)

[2] 王 静，吴 庆，周亚运. 矮塔斜拉桥临时固结体系模拟方案研究[J].南京工程学院学报，2016，2(14):23-28. Wang Jing， Wu Qing， Zhou Yayun. Simulation research into temporary consolidation of extra-dosed cable-stayed bridges[J]. Journal of Nanjing Institute of Technology.2016，2(14):23-28.(in Chinese)

[3] 刘 昀，颜东煌.部分预应力混凝土斜拉桥设计的合理性分析[J].中外公路，2015，35(2):83-86. Liu Yun，Yan Donghuang. Rationality analysis of partial prestressed concrete cable stayed bridge[J]. Journal of China and Foreign Highway，2015，35(2):83-86.(in Chinese)

[4] 方秦汉.芜湖长江大桥[J].华中科技大学学报城市科学版，2002，19(1)：1-3. Fang Qinhan. Wuhu Yangtze river bridge[J].Journal of Huazhong University of Science and Technology Urban Science Edition，2002，19(1)：1-3.(in Chinese)

[5] 吴节松.宽幅矮塔斜拉桥的部分关键技术研究[D].合肥：合肥工业大学，2014. Wu Jiesong. Research on the key technology of the wide extra-dosed cable-stayed bridge[D].Hefei：Hefei Polytechnic University，2014.(in Chinese)

[6] 肖汝诚，卫 璞，孙 斌，等.大跨度部分地锚斜拉桥力学分析与参数研究[J].东南大学学报自然科学版，2013，43(5)：1097-1103. Xiao Rucheng，Wei Pu，Sun Bing，et al. Mechanical analysis and parametric study of long-span partially earth-anchored cable-stayed bridge[J].Journal of Southeast University Natural Science Edition，2013，43(5)：1097-1103.(in Chinese)

[7] 贺拴海.桥梁结构理论与计算方法[M].北京：人民交通出版社，2003. He Shuanhai. Theoretical and computational methods of bridge structure[M]. Beijing： China Communications Press，2003. (in Chinese)

[8] 王凌波，彭晶蓉，贺拴海. 预应力混凝土部分斜拉桥拉索与预应力筋分配比研究[J].中外公路，2016，36(5):110-114. Wang Lingbo，Peng Jingrong， He Shuanhai. Research on distribution ratio of cable and pre-stressing steel wire in pre-stressed concrete extra-dosed cable stayed bridges[J]. Journal of China and Foreign Highway，2016，36(5):100-104.(in Chinese)

[9] 彭晶蓉，贺拴海，王凌波. 基于模型试验的曲线部分斜拉桥施工过程模拟分析[J].铁道科学与工程学报，2016，13(11):2190-2197. Peng Jingrong， He Shuanhai，Wang Lingbo. Simulation and analysis of the curved extra-dosed bridge construction based on model test[J]. Journal of Railway Science and Engineering，2016，13(11):2190-2197.(in Chinese)

[10] 孙淑红.外倾索面PC箱梁部分斜拉桥受力性能研究[D].重庆：重庆交通大学，2012. Sun Shuhong. Behaviors of Pre-stressed concrete box girder for partially cable-stayed bridges with double outwardly inclined cable planes[D].Chongqing：Chongqing Jiaotong University，2012.(in Chinese)

[11] 杨庆国.矮塔斜拉桥布索方式计算研究[J].交通标准化，2009，9(19):63-67. Yang Qingguo. Disposition of cable in extra-dossed cable-stayed bridge[J]. Transport Standardization，2009，9(19):63-67.(in Chinese)

[12] 刘昊苏.不同布索形式下曲线矮塔斜拉桥静动力性能研究[D].北京：北京建筑大学，2013. Liu Haosu.The Investigation ion the static and dynamic behaviors of the curved extra-dosed cable-stayed bridges with different cable-styles[D].Beijing：Beijing Architecture University，2013.(in Chinese)

[13] 张力文，夏睿杰，肖汝诚，等.部分地锚式斜拉桥合理成桥状态二阶段确定法[J].深圳大学学报理工版，2012，29(1):51-55. Zhang Liwen，Xia Ruijie， Xiao Rucheng， et al.The two-stage method to determine the reasonable completed status of partially earth-anchored cable-stayed bridge[J]. Journal of Shenzhen University Science and Engineering，2012，29(1)51-55.(in Chinese)

[14] 赵晓晋，贺拴海，白鹭涛. 双塔斜拉-连续梁组合体系的力学行为分析[J].深圳大学学报理工版，2016，33(5)：492-500. Zhao Xiaojin，He Shuanhai，Bai Lutao．Mechnical behavior analysis of double-pylon cable-stayed-continuous beam combination system [J]．Journal of Shenzhen University Science and Engineering，2016，33(5)：492-500．(in Chinese)

[15] 杨 飞.山区曲线部分斜拉桥结构体系与结构性能研究[D].西安：长安大学，2011. Yang Fei.Study for structure system and structure performance of curve extra-dosed cable-stayed bridges in the mouritairis[D].Xi’an：Chang’an University，2011.(in Chinese)

[16] 赵晓晋，贺拴海，李 源，等．斜拉桥前支点挂篮施工过程模拟分析[J]．深圳大学学报理工版，2017，34(2)：138-146． Zhao Xiaojin， He Shuanhai， Li Yuan， et al. Process simulation of fore fulcra form traveller construction for cable-stayed bridge[J]. Joumal of Shenzhen University Science and Engineering，2017，34(2)：138-146.(in Chinese)

[17] 黄汪胜.大跨预应力连续箱梁桥矮塔斜拉加固布索方式.研究[D].南京：南京航空航天大学，2011. Huang Wangsheng. Research on cable arrangements of long-span pre-stressed continuous box girder bridge with low tower cable-stayed reinforcement[D].Nanjing： Nanjing University of Aeronautics and Astronautics.(in Chinese)

[18] 陈爱军，邵旭东，李立峰，等.无背索竖琴式斜拉桥拉索索力敏感性分析[J].华东公路，2008，31(4)：3-6. Chen Aijun, Shao Xudong, Li Lifeng, et al. Cable force sensitivity analysis of cable stayed bridge without back cable[J]. East China Highway，2008，31(4)：3-6.(in Chinese)

[19] 兰 彬.背索布索方式对独塔斜拉桥结构性能影响分析[D].西安：长安大学，2011. Lan Bin.Analysis on structure performance of single inclined pylon cable-stayed bridge under different kinds of back-stay’s cable layout[D].Xi’an：Chang’an University，2011.(in Chinese)

[20] 陈从春. 矮塔斜拉桥设计理论核心问题研究[D]. 上海：同济大学，2006. Chen Congchun. Study on major problems for design theory of extra-dosed cable-stayed bridges[D]. Shanghai： Tongji University，2006.(in Chinese)

[21] 吴益炳，陈仕刚.部分斜拉桥索梁活载比计算公式的推导[J]公路，2016，61(11):144-148. Wu Yibing，Chen Shigang. The formula derivation about distribution ratio of live load between cable and beam in extra-dosed cable-stayed bridge[J].Highway，2016，61(11):144-148.(in Chinese)

[22] 刘 凯.曲线部分斜拉桥的几个设计参数研究[D].西安：长安大学，2013. Liu Kai. Study on several design parameters of curve extra-dosde cable-stayed bridge[D].Xi’an：Chang’an University，2013.(in Chinese)

[23] 杨 可. 矮塔斜拉桥动力特性及地震响应分析[D]大连：大连海事大学，2016. Yang Ke. Research on dynamic behavior and seismic response of extra-dosed cable-stayed bridges[D]Dalian：Dalian Maritime University，2016.(in Chinese)

[24] 毕树兵.矮塔斜拉桥墩顶不平衡转体施工关键技术研究[J].公路交通科技，2011，7(12):238-241. Bi Shubing. Research on unbalanced swivel construction of extra-dosed cable-stayed bridges[J]. Journal of Highway and Transportation Research and Development，2011，7(12):238-241.(in Chinese)

【中文责编：坪梓；英文责编：之聿】

Comparisonofcabledesignsbasedonthedistributionratiobetweencableandbeamofextra-dosedbridge

PengJingrong1,HeShuanhai1,andLiYao2

1)SchoolofHighway,Chang’anUniversity,Xi’an710064,ShaanxiProvince,P.R.China2)CCCCFirstHighwayConsultantsCo.Ltd,Xi’an710075,ShaanxiProvince,P.R.China

The formula of live load ratio between the cable and beam for the rigid system extra-dosed bridge is derived, and the concept of cable quantity is put forward for different cable layouts. For extra-dosed bridge, the larger the angle between cable and girder is (less than54.74°), the more live load born by cables, so the ratio of radial layout is the maximum, then that of the fan-shaped layout, and the ratio of harp-shaped layout is the minimum. However, the length for three cable layouts is exactly opposite. Therefore, when the initial design of the extra-dosed bridge is completed, the most economical cable layout can be chosen based on the cable quantity. Finite element models of three cable layouts for an extra-dosed bridge are set up. The results show that in order to achieve the expected live load ratio between the cable and beam, the cable quantity for the radial cable layout is the least, followed by that of the fan-shaped layout which is25% more than the cable quantity of the radial cable layout. The cable quantity of the harp-shaped layout is the most which is81% more than that of the radial cable layout. The finite element analysis results are consistent with the calculated ones by the simplified formula with only a difference of8%.

bridge engineering; extra-dosed bridge; cable layout; radial layout; fan-shaped layout; harp-shaped layout; distribution ratio; cable quantity

2017-01-04；Accepted：2017-04-18

Professor He Shuanhai．E-mail：heshai@chd.edu.cn

U 442；U 448.27

：Adoi：10.3724/SP.J.1249.2017.05482

Foundation：Science and Technology Project of Guangdong Provincial Transportation Department (2014-02-017)

：Peng Jingrong, He Shuanhai, Li Yao．Comparison of cable designs based on the distribution ratio between cable and beam of extra-dosed bridge[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(5): 482-487.(in Chinese)

广东省交通运输厅科技项目(2014-02-017)

彭晶蓉(1988—)，女，长安大学博士研究生.研究方向：桥梁结构理论研究.E-mail：pjrgreen6@163.com

引文：彭晶蓉，贺拴海，李 尧．基于索梁活载比的部分斜拉桥布索形式比较[J]. 深圳大学学报理工版，2017，34(5)：482-487.