聚类集成中基聚类的优化研究
2017-09-23钟才明庞永明
程 凯 钟才明 庞永明
1(宁波大学信息科学与工程学院 浙江 宁波 315210)2(宁波大学科学技术学院信息工程学院 浙江 宁波 315210)
聚类集成中基聚类的优化研究
程 凯1钟才明2庞永明1
1(宁波大学信息科学与工程学院 浙江 宁波 315210)2(宁波大学科学技术学院信息工程学院 浙江 宁波 315210)
聚类集成是将一个数据集的多个划分(基聚类)合成一个新的聚类,该聚类最大程度地代表了所有输入基聚类对数据集的聚类信息。显而易见,初始基聚类的质量对于最终的集成划分至关重要。传统的聚类集成中的基聚类器使用最多的是K-means,因为K-means不仅实现简单,计算复杂度不高,而且其聚类机制符合机器学习关于局部数据的类别条件概率为常数的假设。但由于K-means通常直接使用高斯距离作为距离测度,其只能发现球形簇的类;而对于具有结构复杂、尤其是基于连接性且非球形分布的类结构的数据集,不能生成高质量(即同质性高)的基聚类。为此提出一个基聚类的优化方法,即:判定K-means所生成类的同质性,对同质性较差的类进行再次划分,以提高基聚类的同质性,从而提高整个聚类集成的质量。在8个数据集上的实验数据表明所提出的方法是有效的。
聚类集成 K-means 基聚类 同质性 伪高斯
0 引 言
采聚类分析已经成为模式识别、机器学习、数据挖掘研究领域的一个非常活跃的研究课题,在识别数据的内在结构方面具有极其重要的作用。根据数据在类中的聚集规则以及应用这些规则的方法,有多种聚类算法[1-2]。但是没有一种聚类算法能准确揭示各种数据集内部所呈现出来的多种多样的簇结构[3]。所以聚类集成成为了另一个重要且有效的手段,它对原始数据集的多个聚类结果进行学习和集成,得到一个能较好地反映数据集内在结构的数据划分。
聚类集成可以这样描述:给定一个聚类结果集合, 聚类集成的目标就是要寻找一个聚类, 使其相对于所有的输入聚类结果来说,尽可能多地符合(或一致)[4]。聚类集成的方法有两个步骤:对原始数据进行不同的基聚类和合并基聚类生成最终的划分[5](如图1所示)。

图1 聚类集成的一般过程
聚类集成的第一步是生成基聚类。通常在集成学习中,集群的差异度被认为是影响集成结果的关键因素之一[6],所以这一阶段需要产生多个具有差异度的基聚类结果,差异从不同的方面反映数据集的结构,有利于集成。这一阶段是对数据集或其子集反复运行聚类算法,有以下几种方法:
(1) 使用一个聚类算法,每次运行都设置不同的参数和随机初始化[7];
(2) 使用不同的聚类算法,如K-means、SL(Single-Linkage)、CL(Complete-Linkage),AL(Average-Linkage)等产生多个不同的聚类[7];
(3) 将数据集的特征空间投影到数据子空间,有随机投影和一维投影等手段[7,9];
(4) 对数据集的子集进行聚类,子集可通过采样如Sub-sampling,Bagging,Bootstrap和随机采样等方法获得[7,10-12]。
聚类集成的第二步是合并基聚类,得到一个统一的聚类结果。目前存在许多合并基聚类的方法,如投票法[7]、超图划分[6]、基于有效性指标的集成方法[8]。
本文主要是针对聚类集成第一步中基聚类的质量提出了一种优化方法,即判定基聚类中每个类的同质性,对同质性较低的类进行二次处理,以提高基聚类的同质性,生成高质量的基聚类。
目前大多数聚类集成中基聚类采用的方法是K-means,因为集成中需要较多的基聚类,而K-means实现简单,计算复杂度不高,执行速度快[13]。但K-means适宜发现球形簇的数据集,对于结构复杂的数据集,尤其是边界不易区分、非球形分布以及高维数据,不能产生较好的聚类结果,所以它生成基聚类还是有缺陷[14]。
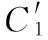
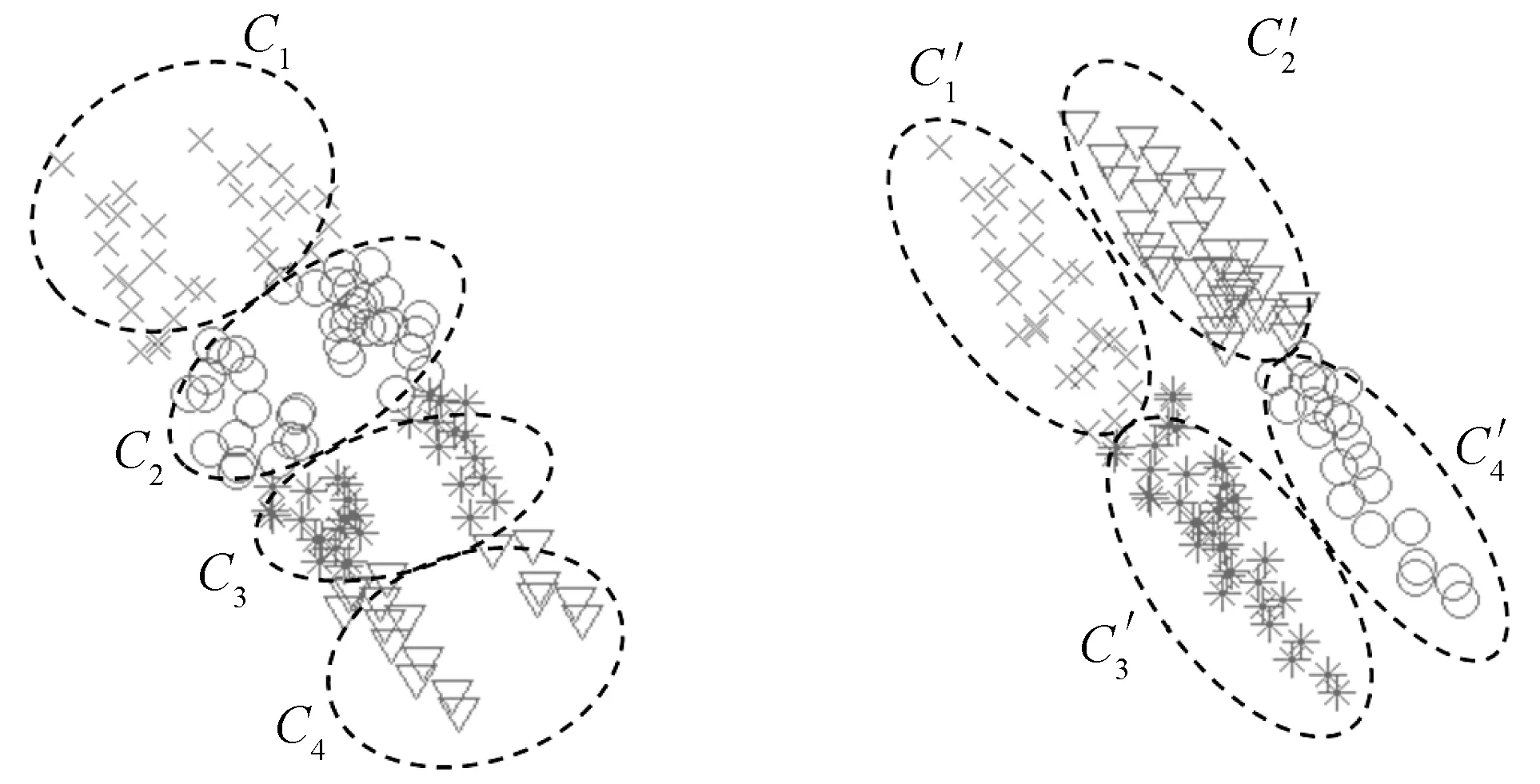
(a) 存在伪高斯的基聚类 (b) 理想的基聚类图2 同一数据集不同的基聚类结果
本文提出的基聚类算法大致流程如图3所示。为了生成多个具有差异度的基聚类,采用聚类集成中常用的基聚类方法K-means进行多次聚类。每一个基聚类结果都是由K-means划分成的多个小高斯簇组成,其中有一些高斯簇并不是一个真实的高斯,而是由若干个更小的高斯簇组成。对于基聚类中的每个高斯簇,分别计算它的覆盖率。覆盖率是反映高斯簇同质性高低的一个重要指标,通过它可以找出同质性较低的高斯簇,即伪高斯。对于找出的伪高斯,并不知道它是何种结构,所以分别采用K-means和SL对其进行二分,选择其中较好的一种处理结果作为优化后的基聚类结果。对基聚类中的每一个伪高斯都作如上处理,生成最终高质量的基聚类。

图3 本文方法实现的示意图
1 伪高斯的判别
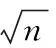
对于每一个高斯簇,可以利用它的均值Mu和协方差矩阵Sigma生成一个标准的高斯分布。将生成的高斯覆盖在原来的高斯上,观察覆盖情况,会发现对于伪高斯,它的结构、形状和生成的标准高斯差异太大,所以重合的部分较少,即覆盖率低(如图4(a)所示);而对于真实高斯,通过它生成的也是一个标准的高斯,他们的形状、结构差异不大,重合的部分较多,即覆盖率高(如图4(b)所示)。

(a) 伪高斯 (b) 真实高斯图4 不同高斯簇的覆盖情况
对于覆盖率的概念,也可以使用密度的概念来描述。对一个数据集,数据点分布密集的区域,密度较高,数据点分布稀疏的区域,密度较低。对图4中的两个数据集,生成相应的密度估计图(如图5所示)。图5(a)中,伪高斯的密度曲线有两个波峰,而生成的标准高斯只有一个波峰,且与伪高斯的波峰所在位置完全不一样。根据生成的标准高斯中每个点在两个密度曲线中的密度计算差值,找出覆盖的点,可以得到同样的结论:重合部分较少,覆盖率低。相反,对于图5(b),原本的高斯与生成的标准高斯所描绘的密度曲线都有一个波峰且位置几乎相同,根据密度差值计算出大部分点都是覆盖的点,重合的部分较多,覆盖率高。
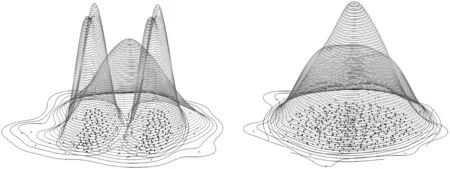
(a) 伪高斯 (b) 真实高斯图5 不同高斯簇的密度分布情况
判别伪高斯的具体方法是,对于每一个高斯簇,定义这个集合为X_Old={xi,xi+1,…,xj},集合中点的个数为Num,利用集合X_Old的均值Mu和协方差矩阵Sigma生成标准的高斯分布数据集X_New={xm,xm+1,…,xn}。
对于X_New中的每一个点xm,采用最近邻算法,找到X_Old中距离xm最近的一个点xi,并计算出它们的欧式距离Dism,即
Dism=min{dis(xm,xi)xm∈X_New,xi∈X_Old}
(1)
这里会设定一个距离阈值delta,对X_New中每一个点,当Dism小于delta,便认为该点是覆盖在原来高斯上的点,加入到集合X_Cover中:
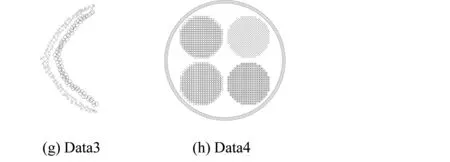
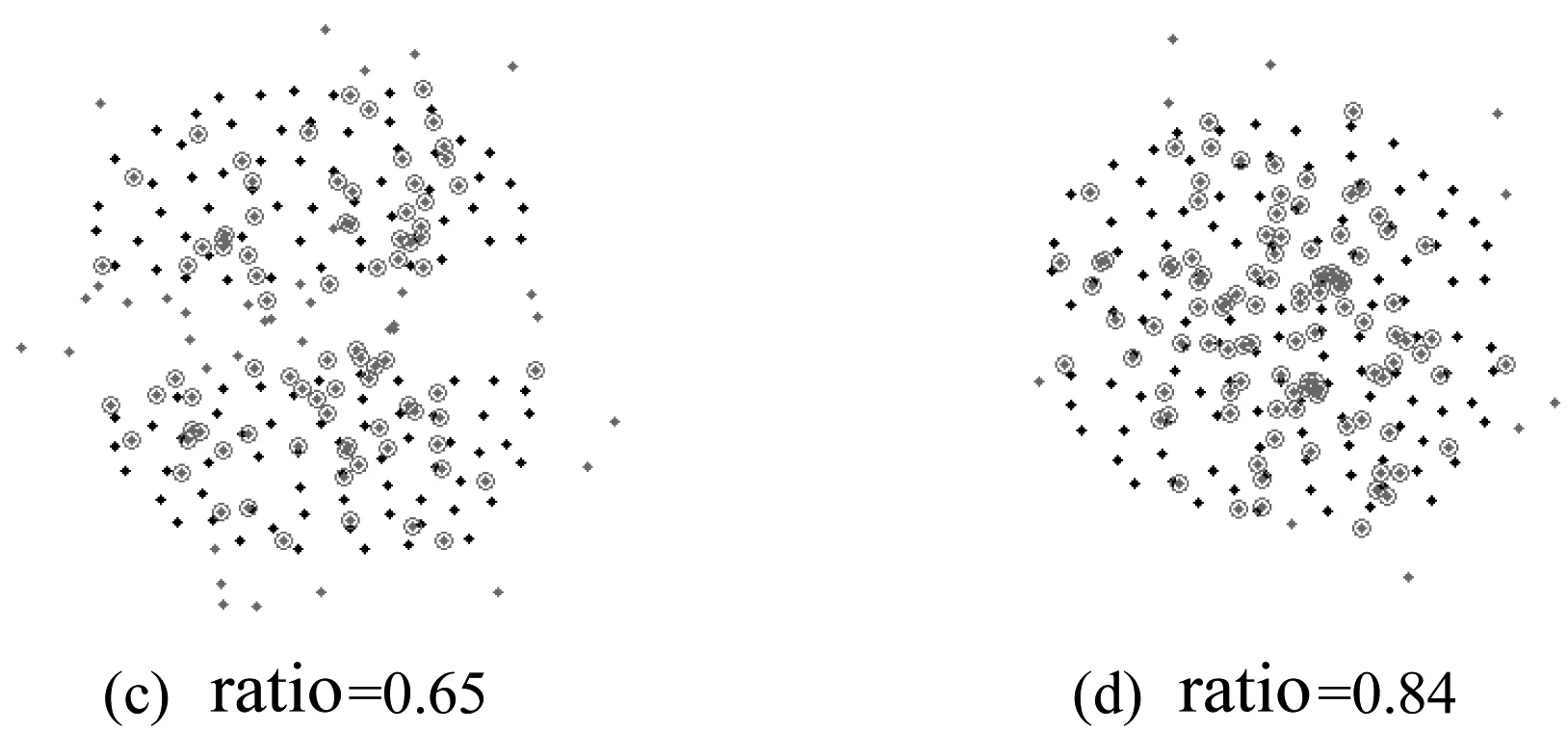
X_Cover={xkxk∈X_New,Disk (2) delta的计算如下:显而易见,对于伪高斯(如图4(a)所示),Dism的波动幅度较大,而对于非伪高斯(如图4(b)所示),Dism的波动幅度较小,因此可以对基聚类的每一个集合求方差Var={Var1,Var2,…,VarK},并作归一化处理: Vari=(Vari-Varmin)/(Varmax-Varmin) (3) Vari作为参数delta的影响因子,这里delta定义如下: (4) 其中Dis_ave=Dism/Num,即最小距离Dism的均值。 经过上面的处理会得到集合X_Cover,集合中点的个数为Num_Cover,集合中所有的点都覆盖在原来高斯上。这样便可以计算出每个高斯的覆盖率: ratio=Num_Cover/Num (5) 其中,这里需要设定一个覆盖率阈值beta=0.75,具体beta的大小将在实验阶段进行讨论。当ratio小于阈值时,便可以判断该高斯为伪高斯。这样就通过基于距离计算覆盖率的方法,找出了伪高斯。具体算法流程见算法1。 算法1 步骤1使用K-means基聚类得到K个类; 步骤2根据每一个类X_Old的均值Mu和协方差矩阵Sigma生成标准高斯X_New; 步骤3对X_New中每一个点,计算X_Old中距离它最近点的欧式距离Dism; 步骤4通过距离阈值delta筛选出X_New中覆盖在原来集合X_Old上的点,加入到集合X_Cover中; 步骤5利用X_Cover中点的个数Num_Cover和X_New中点的个数Num_Cover,计算每个类的覆盖率ratio,并与阈值beta作比较,判断该类是否为伪高斯。 由于基聚类是由K-means划分成的多个小高斯簇组成,高斯簇的个数较多,每个高斯簇的点较少,高斯簇的结构比较简单,所以伪高斯的结构也比较简单。一般具有两种结构:高斯球形簇结构和基于连接的结构,直接采用二分就可以将其划分开。这里有提供两种方法对它进行处理:第一种方法,利用K-means对伪高斯进行二分,K-means对高斯结构的数据集能够较好的进行处理;第二种方法,利用SL对伪高斯进行二分,SL对基于连接的数据集有较好的处理能力。 定义集合X_Found={xa,xa+1,…,xb}为伪高斯,利用K-means对其二分,得到两个类X_Found11、X_Found12和二分后的分类标签C1;同时,利用SL对X_Found二分,得到两个类X_Found21、X_Found22和二分后的分类标签C2。 对于X_Found,如果二分的效果很好,则利用算法1分别对划分开的两个类计算覆盖率,得到的两个覆盖率结果应该是较高的。反之,如果二分的效果不好,计算出的覆盖率应该很低。这可以作为选择何种二分方法的依据。 基于以上考虑,对K-means二分结果X_Found11和X_Found12利用算法1计算两个类的覆盖率得到ratio11、ratio12。同时对SL二分结果X_Found21、X_Found22也作相同计算得到覆盖率ratio21和ratio22。这样便可计算出K-means划分的综合覆盖率ratio1和SL划分的综合覆盖率ratio2: ratio1=ratio11+ratio12 (6) ratio2=ratio21+ratio22 (7) 选择其中覆盖率较大的一种二分结果作为最终伪高斯的划分结果,用公式表示: (8) 这样便得到伪高斯处理之后的类标签Ci。具体算法流程见算法2。 算法2 步骤1K-means对伪高斯X_Found二分,得到两个类X_Found11、X_Found12和二分后的分类标签C1; 步骤2SL对伪高斯X_Found二分,得到两个类X_Found21、X_Found22和二分后的分类标签C2; 步骤3对X_Found11、X_Found12、X_Found21和X_Found22利用算法1,计算覆盖率ratio11、ratio12、ratio21和ratio22; 步骤4计算K-means二分方法的综合覆盖率ratio1和SL二分方法的综合覆盖率ratio2; 步骤5选择覆盖率大的一种二分结果作为伪高斯的分类标签Ci。 对于每一个基聚类中出现的伪高斯都作如上处理,便可得到优化之后的基聚类结果E={C1,C2,…,CK}。 有了高质量的基聚类,无疑将提高最终集成的质量,本文在优化基聚类之后,采用了Strehl提出的方法[7]进行集成,具体的实验结果在下一节中说明。 3.1 集成结果比较 实验采用8个不同的数据集分别进行聚类集成,其中Path-based、Spiral、Jain和S1四个数据集来自http://cs.uef.fi/sipu/datasets;Data1、Data2、Data3和Data4为四个人工描绘的数据集。集成部分采用Strehl提出的方法[7]。图6是直接K-means基聚类对8个不同形状的数据集集成的结果,图7是本文方法对8个数据集集成的结果。 图6 基于K-means基聚类的集成结果 图7 基于改进基聚类方法的集成结果 表1中的数据为50次集成准确率的均值。所选的8种数据集内部较为复杂,具有很好的代表性,Path-based、Jain、S1和Data4四个数据集内部结构复杂,既有球形分布也有非球形分布,且有边界不易区分的部分。K-means基聚类对这些地方没有很好的处理,不能产生质量较高的基聚类结果。改进的基聚类算法对这些易产生同质性较低划分的地方作了处理,一定程度上提高了集成的效果。Spiral、Data1、Data2和Data3四个数据集属于基于连接性且非球形分布的类结构的数据集,K-means不能生成高质量的基聚类,所以集成的效果也一般,改进的基聚类算法对这类数据能较好的处理,大大提高了聚类集成的效果。 表1 K-means基聚类算法和改进基聚类算法的集成准确率 3.2 基聚类中类数目K的讨论 图8 基聚类算法不同K取值时的集成准确率 3.3 覆盖率阈值beta的讨论 算法1中基聚类的每个类计算出的覆盖率与beta进行比较,当覆盖率小于beta时,则判断该类为伪高斯,并作进一步处理,反之则不作处理。所以beta的大小非常关键,直接影响判断伪高斯的正确与否,需要进行大量的实验来确定beta的取值。 图9表示两个高斯簇逐渐靠近变化为一个高斯簇的过程中覆盖率的变化情况,可以发现两个高斯簇越靠近,覆盖率越高,当两个高斯簇合并为一个高斯簇时覆盖率达到最高。经过大量数据集的实验与分析,表明beta=0.75是一个较合理的取值,可以作为覆盖率阈值准确判断一个类是否为伪高斯。 图9 两个高斯簇逐渐靠近变化为一个高斯过程中覆盖率变化情况 本文对聚类集成中传统的基聚类方法进行优化,建立一个能产生更好基聚类的算法,对提高聚类集成的质量有显著的效果。改进的方法重点解决如何通过类与类之间的覆盖率在无类标签的情况下判断类的同质性,找到同质性低的类,并对其作精化处理,得到更好的基聚类,以完成更好的聚类集成。 但是这种算法依然存在一些局限性,对一些高维的数据集聚类效果不是很好。分析可知,覆盖率计算中使用欧氏距离作为距离测度,这种方法不能很好地表现出一些高维数据集中点与点之间的距离。其次,对于基聚类中出现同质性较低的伪高斯情况较少的数据集,它的集成结果提高有限。因为同质性较低的伪高斯是影响集成效果的关键,本算法针对的是基聚类中出现伪高斯情况较多的数据集,对这样的数据集有较大的改进。本方法存在一些不足,也是未来一段时间需要做的工作。 [1] Duda R O, Hart P E, Stork D G. Pattern classification[M]// Pattern classification. Wiley, 2001:119-131. [2] Jain A K, Dubes R C. Algorithms for clustering data[J]. Technometrics, 1988, 32(2):227-229. [3] 孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008, 19(1): 48-61. [4] Gionis A, Mannila H, Tsaparas P. Clustering aggregation[J]. ACM Transactions on Knowledge Discovery from Data, 2007, 1(1): 1-30. [5] Sandro Vega-pons, Jose Ruiz-shulcloper. A Survey of Clustering Ensemble Algorithms[J]. International Journal of Pattern Recognition and Articial Intelligence, 2011, 25(3): 337-372. [6] 罗会兰, 孔繁胜, 李一啸. 聚类集成中的差异性度量研究[J]. 计算机学报, 2007, 30(8): 1315-1324. [7] Strehl A, Ghosh J, Cardie C. Cluster ensembles: A knowledge reuse framework for combining multiple partitions[J]. Journal of Machine Learning Research, 2002, 3(3): 583-617. [8] 王海波, 徐涛. 基于有效性指标的聚类集成学习方法[J]. 计算机应用与软件, 2012, 29(9): 45-49. [9] Topchy A, Jain AK, Punch W. Combining multiple weak clusterings[J]. IEEE international conference on data mining, 2003, 1(1): 331-338. [10] Dudoit S, Fridlyand J. Bagging to improve the accuracy of a clustering procedure[J]. Bioinformatics, 2003, 19(9): 1090-1099. [11] Fraley C, Raftery AE. How many clusters? Which clustering method? Answers via model based cluster analysis[J]. The Computer Journal, 1998, 41(8): 578-588. [12] Minaei-Bidgoli B, Topchy A, Punch W. Ensembles of partitions via data resampling[J]. Proceedings of international conference on information technology, 2004, 2(2): 188-192. [13] Iam-On N, Boongoen T, Garrett S, et al. A Link-Based Approach to the Cluster Ensemble Problem[J]. IEEE Transactions on Software Engineering, 2011, 33(12):2396-2409. [14] 韩最蛟. 基于数据密集性的自适应K均值初始化方法[J]. 计算机应用与软件, 2014, 31(2): 182-187. REFINEMENTOFBASECLUSTERSFORCLUSTERINGINTEGRATION Cheng Kai1Zhong Caiming2Pang Yongming11 (CollegeofInformationScienceandEngineering,NingboUniversity,Ningbo315210,Zhejiang,China)2(CollegeofScienceandTechnology,NingboUniversity,Ningbo315210,Zhejiang,China) Cluster ensemble integrates the multiple partitions of a dataset into a new clustering, which discloses the cluster structure information of all the base clusters to the greatest extent. The qualities of base clusters are obviously crucial to the final ensemble result. K-means is one of the most used algorithms to produce base partitions, as it can be implemented easily and the corresponding computational cost is low, and furthermore, its clustering mechanism conforms to the assumption in machines learning that the class conditional probability of local data is a constant. But K-means usually adopts Gaussian distance as the distance measure, thus it can only find the clusters of spherical shape. It is also unable to generate high-quality base clusters when applied to datasets with complex structures, especially those whose class structures are not distributed spherically but based on connectivity. Therefore, this paper presents an optimization method for base clusters, namely, to judge the homogeneity of the clusters generated by K-means and partition those with poor homogeneity once again to improve the homogeneity. As a result, the quality of the entire cluster ensemble is improved. The experiments on 8 datasets demonstrate the effectiveness of the proposed method. Clustering integration K-means Base clusters Homogeneity Spurious Gaussian TP18 A 10.3969/j.issn.1000-386x.2017.09.052 2016-08-27。国家自然科学基金项目(61175054)。程凯,硕士生,主研领域:模式识别,机器学习。钟才明,教授。庞永明,硕士生。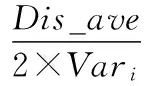
2 伪高斯的精化
3 实验结果与分析
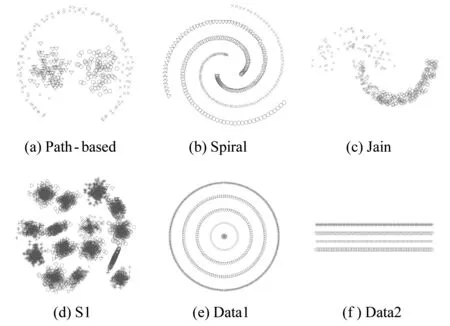


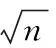
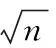


4 结 语
