四维CT肺图像多层次时空一致性配准方法

杨 浩 胡冰锋 孙瑞芳 杨 烜*

1(西安电力高等专科学校 陕西 西安 710032)2(深圳大学计算机与软件学院 广东 深圳 510086)

四维CT肺图像多层次时空一致性配准方法

杨 浩1胡冰锋2孙瑞芳2杨 烜2*

1(西安电力高等专科学校 陕西 西安 710032)2(深圳大学计算机与软件学院 广东 深圳 510086)

四维CT肺图像提供了肺部动态信息，可广泛用于肺部疾病诊断和精确放射治疗。提出一种针对四维CT肺图像的多层次时空一致性配准方法。该方法首先从最大吸入相位的图像中提取控制点，利用结构张量跟踪算法对控制点进行跟踪；构建多层时空一致性优化模型，对控制点进行调整，从整图配准角度提高控制点配准精度；每次调整后根据配准的一致性误差，添加新的控制点，进一步降低配准的一致性误差，并对新的控制点集重新进行优化调整。该模型在空间上对形变进行约束，保持形变扭曲的平滑性；在时间上对控制点轨迹进行约束，保持控制点的轨迹平滑性；通过一致性约束，降低了正向和反向形变函数的一致性误差。在测试数据集上的实验结果表明，该方法可以得到平滑、稳定、合理的形变结果，可以用于估计肺部运动模型。

图像配准 CT图像 一致性形变 时空约束

0 引 言

CT成像技术已广泛用于医学图像研究领域。近些年，三维CT成像技术已经发展到四维成像，即在三维图像的基础之上加上时间维度，构成一系列离散的三维图像集合。四维CT成像可以用于研究肺部的生理特征，基于4DCT的图像配准技术可以得到肺部的运动模型。该模型可以用于图像引导放疗领域，为图像引导放疗提供更准确的肺部运动信息(包括肿瘤运动)，结合精确放疗技术，减少放射量对正常组织的损伤，提高肺癌的治疗效果[1]。

图像配准就是估计浮动图像与目标图像之间的形变函数，使浮动图像经过形变之后与目标图像的差异尽可能小。由于四维图像在时间轴的关联性，四维配准并不是简单的多个三维图像配准，其求解的形变函数不仅仅要考虑诸如空间平滑约束，还需考虑时间平滑、正反形变的一致性约束等。所谓空间平滑指的是某个特定时间的空间形变具有较低的扭曲能量；时间平滑指器官随时间变化形成稳定的运动轨迹，没有大幅度的震荡；一致性约束是指正向和反向形变之间满足相互可逆的条件，这样得到的形变更具生物学意义[2]。目前空间平滑和空间平滑约束已有较成熟的研究成果[3-4]，而一致性约束是一个比较困难且仍在进行研究的问题。

一致性图像配准要求建立浮动图像和目标图像之间的相互可逆的正向和反向形变函数，即浮动图像中的像素点A能映射到目标图像唯一像素点B。反之，目标图像中的点B也都能通过反向形变映射到浮动图像中的点A。而目前大量的图像配准技术并不满足这个约束[5]，这种不一致造成的结果是配准得到的对应关系并不能真正反映图像目标间的对应关系。

目前一致性配准算法主要分为两类，一类如Zhang等[6]提出的基于图像强度信息的一致性配准方法，如一致性demons配准算法，该算法在demons原算法基础上加入一致性的约束；Alvarez等[7]针对稠密光流场引入了双向一致性规约；通过迭代优化一致误差，求解得到一致性形变函数；Ye等[8]在变分弹性模型下提出一种一致性图像配准方法，通过引入残差图像的一致性变换约束提高配准精度；Leow等[9]在线性弹性模型上提出一种同时迭代正反变换的一致性方法，其单向形变函数通过对称代价泛函进行求解，避免计算正反变换的逆函数；Modat等[10]在FFD(Free-Form Deformation)基础上提出了一种一致性对称自由形变算法。

另一类是以Johnson等[2]为代表的基于控制点对的一致性配准方法。这类方法在基于薄板样条的形变函数下加入一致性形变约束，通过迭代逼近求解一致性形变。但是该方法存在控制点对应关系存在误差的问题，同时计算量巨大。Yang等[12]提出了一种快速一致性形变算法，该算法省略了传统算法[2]的求逆步骤，可节省大量的运算。Shen等[13]则提出了代价相对较低的一致性配准优化模型，该模型在代价函数中同时加入一致性约束，通过多次迭代优化使正向形变和反向形变满足互逆条件。

本文提出了一种时空一致性约束优化模型。该模型首先提取控制点，对控制点进行跟踪，在跟踪的基础上利用时空约束优化模型对控制点进行调整，同时加入了空间平滑约束、时间平滑约束和简化的一致性约束。进一步地，在每一次优化之后，又根据形变的一致性误差增加控制点，并对新增控制点进行优化调整，重复该过程，直至一致性误差满足要求。该方法可以提高四维图像配准精度，得到平滑、稳定、满足一致性约束的形变函数。

1 时空一致性配准模型

优化的思想就是构建代价函数，利用跟踪准确的控制点对应关系调整跟踪不准确的控制点。如图1所示，跟踪算法得到所有控制点在不同相位图像中的预测位置，进而根据控制点对应关系，利用薄板样条算法[3]求解浮动图像到所有目标图像的形变函数ft。由于大部分控制点跟踪较为准确，ft可以较好地表达相位间的形变关系，为后期优化调整提供一个理想的初值。优化的思想就是建立目标函数，通过调整控制点的跟踪位置使目标函数达到最优，进而根据调整后的控制点确定形变函数。

图1 4D肺图像配准示意图ft是正向形变，ht反向形变

在优化过程中，代价函数容易陷入局部极值，而控制点的数量越多，优化过程陷入局部极值的可能性越大。针对该问题，本文提出多层次配准方法。该方法在初始控制点基础上进行优化配准，每一次优化之后再根据一致性误差增加新的控制点，并对新增的控制点进行优化调整，直至满足一致性误差的条件，如图2所示。这样就避免了一次性配准中控制点数量过多可能陷入局部极值的问题，同时逐层增加控制点也有助于减少一致性误差。

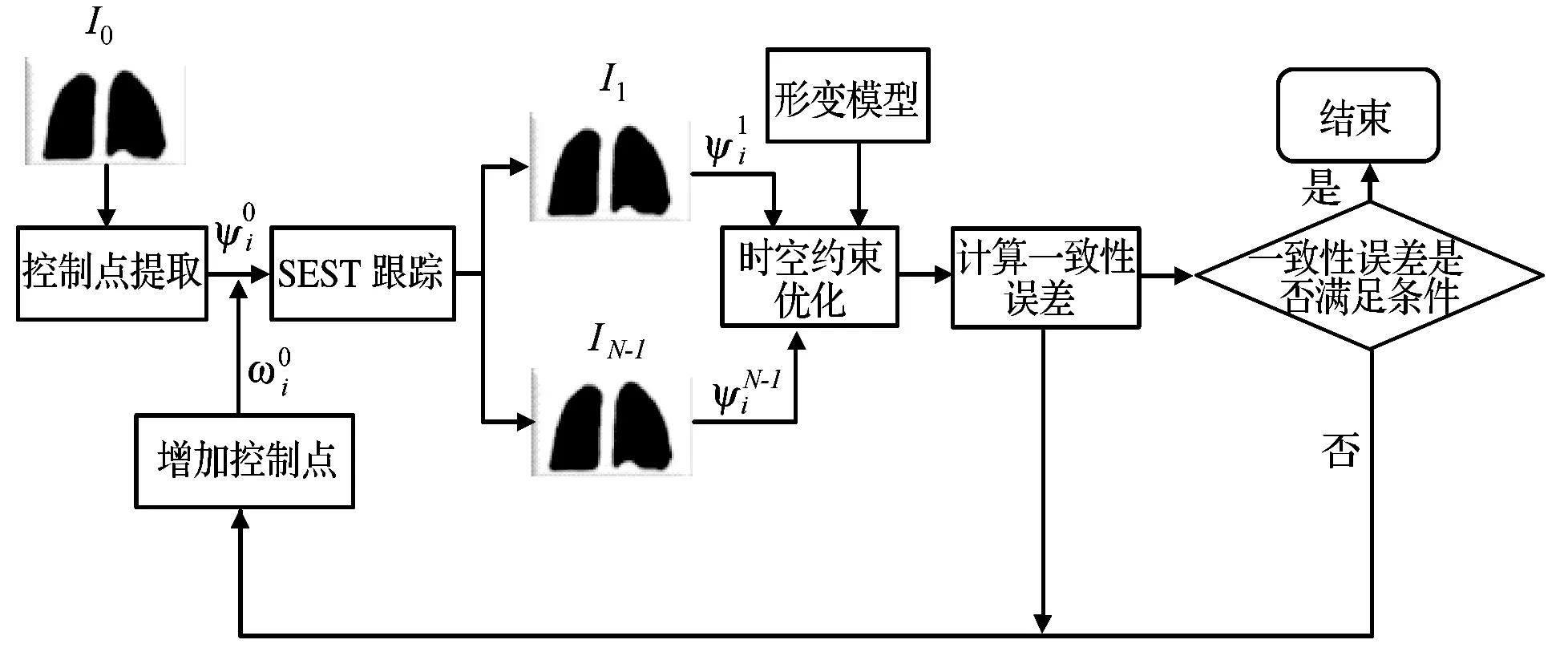
图2 多层次配准流程示意图

1.1 控制点提取与跟踪

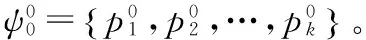
1.2 时空约束优化

根据上述的肺运动特点，本文提出的优化模型考虑以下几个因素：1) 形变图像和目标图像尽可能相似；2) 正向形变和反向形变之间尽可能满足一致性约束；3) 空间形变的扭曲能量尽可能小；4) 控制点的时间轨迹要尽可能平滑。这里的一致性约束并没有严格要求正反形变互逆，而是通过正向和反向形变的配准误差表达一致性约束程度。这种方法是一种简化的一致性误差约束方法，可以避免求解正向形变函数的逆函数，从而减少优化的时间消耗。

本文的时空一致性约束配准模型由三部分组成：

CE(μ)=CESim(μ)+α·CEB(μ)+β·CES(μ)

(1)

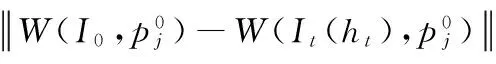
(4)

优化模型中第一部分CESim是相似性度量，用来描述目标图像It和形变图像I0(ft)之间的相似度，以及浮动图像I0和反向形变图像It(ht)之间的相似度，体现了一种简化的一致性约束。如果二者能同时达到最小，也能达到正向形变和反向形变趋于一致的效果。需要说明的是，本文比较的是控制点周围的一个邻域W之间的相似程度，而不是整个三维图像的相似程度，这样处理的目的，主要是为了提高计算效率，同时实验分析也表明这种局部相似度是可行的。

第二部分用来计算正向形变函数ft和反向形变ht的扭曲能量[3]，形变扭曲能量越高表明形变越剧烈。

第三部分计算控制点轨迹的平滑度，肺图像上的点随时间变化的轨迹应该是比较平缓的，剧烈震荡的轨迹往往是配准精度下降的表现。本文采用拉普拉斯算子度量轨迹的平滑度。

本文采用拟牛顿(quasi-Newton)优化算法的改进算法BFGS(BroydenFletcherGoldfarbShanno)求解代价函数CE(μ)。BFGS优化算法具有高精确度和快速收敛的优势，在计算机内存不足、计算量大的情况下可以用L-BFGS(Limited-Memory Quasi-Newton Method)近似。在优化过程中，如果控制点的个数比较多，就选择L-BFGS优化算法。

1.3 形变模型

本文方法中采用薄板样条[3]对形变场进行估计，其中图像中非控制点的形变要靠所有控制点的拉伸作用力去控制。如果控制点过少就会造成远离控制点区域形变误差较大，同时一致性误差会变得更大。如果在一致性误差较大的区域加入新的控制点，既可以保证一致性误差有所改善，同时也可以使新控制点附近区域的形变更准确。

1.4 计算一致性误差

假设当前正向形变函数为f，反向形变函数为h，点x处的正向一致性误差ef和反向一致性误差eh定义如下：

ef=f(h(x))-xeh=h(f(x))-x

(5)

1.5 增加控制点

多层次配准方法的思想就是在少量初始控制点基础上，逐渐增加新的控制点进行更细致的配准，直到满足结束条件为止。增加新的控制点的原则就是基于当前形变的一致性误差。由于控制点上的一致性误差为0，通过在一致性误差较大的区域加上控制点，可以减少新增控制点邻域内的一致性误差，同时也可以提高形变函数的精度。我们把局部范围内一致性误差最大的点列为新增控制点候选，如果候选新增控制点处于非特征结构上(如非血管或非血管分叉等)，可能会导致跟踪困难。所以本文提取一致性误差较大且处于血管结构上的点作为本次迭代新增控制点。

在确定了新增控制点之后，我们采用SEST算法预测新增控制点在所有相位目标图像中的位置，然后通过时空一致性优化模型对这些新增控制点进行调整。将调整后的新增控制点加入到当前层次控制点集中得到新的控制点集，再进行下一层的迭代，这样逐层增加控制点，直至一致性误差满足结束条件。

1.6 配准流程

整个配准过程是通过迭代增加控制点，并调整控制点的位置，以完成对目标的优化，完整过程见2.1节。层次时空一致性配准步骤如下：

Step1在浮动图像I0中提取一定数量的初始控制点集ψ0。设置迭代收敛阈值参数ε，令迭代数i=0。

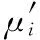
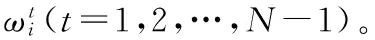
本文算法是在MATLAB R2014a开发环境， Windows Server 2008操作系统环境下实现的。下面附上算法的部分核心代码：

While (iterε) //iter为迭代次数，MaxIter为最

//大迭代次数，一致性误差大于收敛误差

iter=iter+1;

MCE_all(iter)=MCE;

//MCE是平均一致性误差

BCEpointset_all=selectControlPoints(I_ref,CE,iter,init_grid,MCE);

//选择新增加的控制点

var_added_all_5 = pointsCorrdinatesTrack(I_ref,I_tar,

BCEpointset_all);

//对新增控制点进行跟踪

[BCEpointset,var_added_5]=deleteExceptinoalTrackedPoints

(init_grid,var_5,BCEpointset_all,var_added_all_5);

//删除异常跟踪点

var_added_other = getLMOtherPhaseCors(I_ref,BCEpointset,4,cases);

//获取控制点在其他相位的坐标位置

…

var=fminlbfgs(@(x)costfunction(I_ref,x,init_grid,sizeV_new,

weight_cost,cases),var,optim);

//对控制点进行优化调整

[init_grid,var] = changeSamePoints(init_grid,var);

CE = getConsistentError(sizeInit,init_grid,round(var),

size_enlarge,C);

//计算一致性误差

I_CE = double(I).*CE; MCE=sum(I_CE(:))/num_lung_tissue;

//计算平均一致性误差

end

2 实验结果及分析

本文实验环境采用双处理器服务器，Intel Keon CPU E5620，主频2.4 GHz，内存8 GB。通过dir-lab[16]网站提供的四维CT肺数据集验证本文提出方法的有效性。该数据集共有10组不同病人的4D肺CT数据，每组数据提供了从T00到T50相位的6个时间点75个标志点的专家标注位置，这些标志点可用于评估本文方法的配准精度。表1列出了该数据集中图像大小及分辨率。

表1 DIR-lab数据

为了避免胸腔数据的干扰，本文对原始图像进行分割，得到肺实质数据。进一步地，采用文献[17]的方法对肺图像进行血管增强。实验中所用优化参数见表2，其中代价函数空间平滑权重值大于轨迹平滑权重，是因为扭曲能量的计算结果比较大；平均一致性误差阈值为迭代收敛条件，在实验过程中发现，一致性误差阈值过小会导致算法多次迭代，而一致性误差提高并不明显，经过多次实验，得出该参数的合适经验值为0.01。控制点局部邻域窗口大小主要是用于计算目标函数中的局部区域度量。该区域不易过大，过大会带来较大的计算量。该区域也不能过小，过小其统计结果不够稳定；搜索区域大小主要是SEST跟踪时的搜索范围，过大的搜索范围容易发生误匹配，而过小的搜索范围容易找不到对应位置。

表2 配准方法参数列表

2.1 配准误差

本文利用专家标志点来评价多层次时空一致性配准HSCR(HierarchicalSpatio-temporal Consistent Registration,)方法的配准精度，以专家标志点与算法得到的标志点之间的距离(TRE)为评价标准。我们把HTSC的配准结果和文献[18-19]的结果进行对比，表3列出75个控制点的TRE比较。可以看出，HSCR的配准结果在平均误差方面都大幅度优于文献[18]的配准结果，而在标准差方面稍微高于[18]。HSCR在case1-case5的配准精度与文献[19]相当，而在case6至case10实验数据方面，HSCR的配准结果明显好于文献[19]的配准结果。综上分析，从整体的配准误差统计分析来看，HSCR取得了比较理想的配准效果。

表3 以75个标志点的配准误差，括号外为平均误差，括号内为标准差，“*”为没有数据

图3为10组数据中75个控制点的HSCR配准误差分布图，其中每组数据统计的是所有标志点在T10-T50 5个时刻的全部误差。图中可以看出这10组数据中75%的控制点配准误差在2 mm以下，50%的标志点跟踪误差在1 mm以下。表4列出了75个控制点箱线图统计中的离群点信息，num表示离群点个数，mean表示离群点的平均TRE，percent表示离群点所占的比例。从该表中可以看出case1的离群率较高，但是离群平均误差较小；case6、case8和case9的离群平均误差较大，但是离群率还是较小的。HSCR的配准误差标准差较大，但是离群率还是较小的，所以总体的配准性能还是良好的。

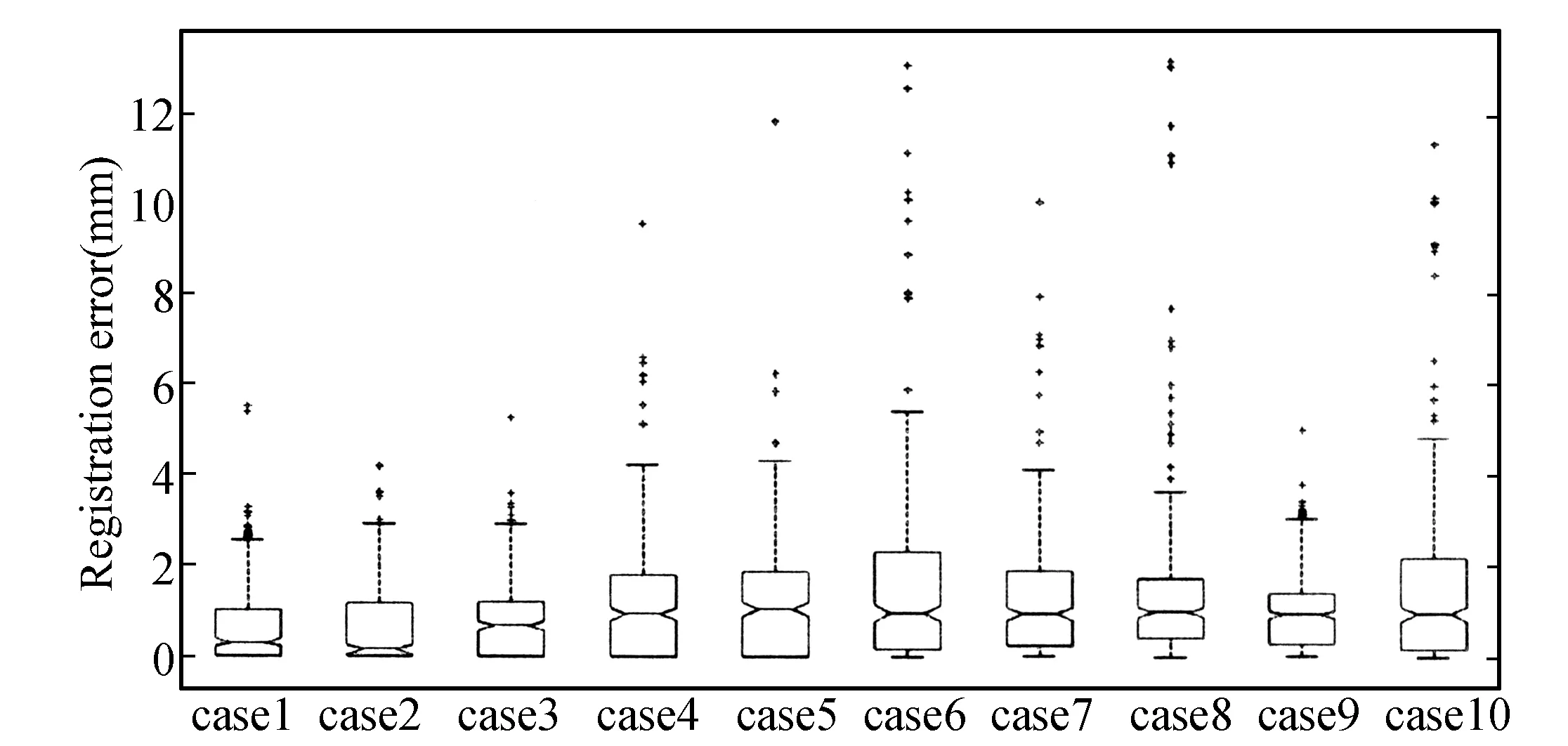
图3 case1-case10 10组数据上75个标志点配准平均误差boxplot分布

Case12345678910num277785129161714mean2.953.493.506.316.659.626.737.543.327.94percent7.2%1.8%1.8%2.1%1.3%3.2%2.4%4.2%4.5%3.7%

为了进一步评价HSCR的配准效果，图4展示了4个样本的配准结果，这4个样本选自呼吸运动较剧烈的case5。其中a为参考相位(T00)一个控制点的局部邻域切片图像；b所在行有两幅图，从左至右分别为配准前所有6个相位(T00-T50)沿着a中横、纵虚线采样的图像强度叠加；c所在行有两幅图，从左至右分别为配准后所有6个相位沿着a中横、纵虚线采样的图像强度叠加。从图中可以看出，配准前同一目标位置有较大差异，导致在b中显示出位移的效果，而配准后同一目标在c中基本是对齐的，这表明配准的结果比较理想。

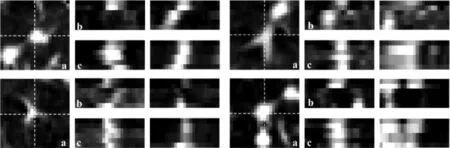
图4 四维肺CT图像配准结果

2.2 一致性误差和平滑性

在保证配准精度达到一定程度的情况下，形变的一致性和平滑性越好，配准的效果也就更加合理。本文将从一致性误差和形变平滑性两方面评价HSCR配准方法。表5列出了一致性配准的统计结果，包括初始控制点数量(Initial Number)、最终收敛控制点数量(Final Number)、迭代次数(Iteration)、初始配准的平均一致性误差(Initial Consistent Error)和最终收敛的配准平均一致性误差(Final Consistent Error)。

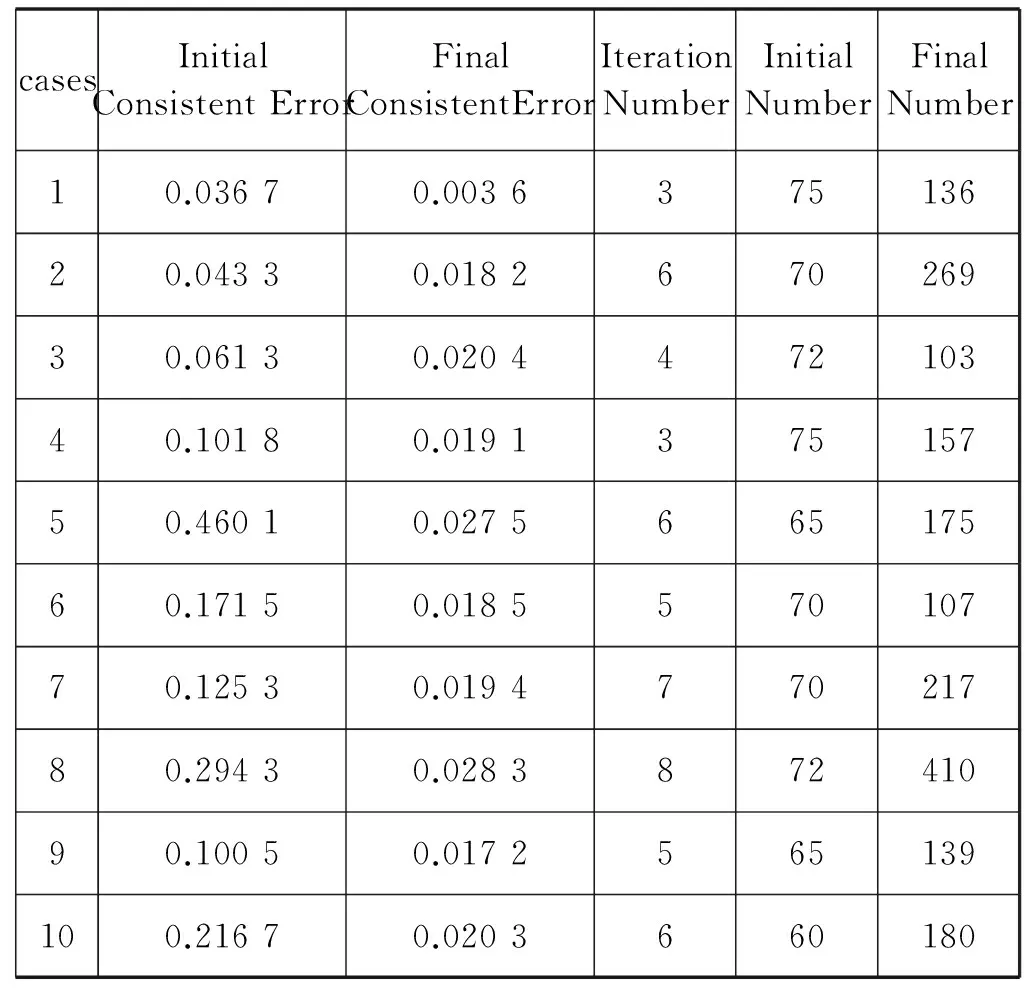
表5 10组数据一致性误差数据统计

从表5可以看出，HSCR收敛后的平均一致性误差比初始控制点得到的平均一致性误差明显下降，而且控制点的数量也随着迭代次数增加而增加，这表明层次增加控制点对于解决配准一致性的问题是有效的。

为了更加详细地表明增加控制点的效果，选取了case4的配准结果进行分析。以case4的第73横断面切片一致性误差为例，如图5所示，可以看出新增的控制点都是位于一致性误差较大的位置(图像越亮，一致性误差越大)“o”为初始控制点位置，“+”增加的控制点位置。(a)的平均一致性误差为0.091 1，最大的一致性误差为0.694 8；(b)的平均一致性误差为0.028 3，最大的一致性误差为0.326 4。上述分析表明HSCR增加的控制点可以使局部区域的一致性误差减小。

图5 增加控制点前后的一致性误差对比

本文将从形变区域的雅可比行列式统计形变的平滑程度，原则上，形变的雅克比行列式越接近1，表明形变扭曲的情况越小，体保持特性更好。本文以case5为例，图6为增加控制点前后形变结果的雅可比行列式直方图统计，其中初始形变的雅可比行列式平均值为0.876 9，配准收敛后形变结果的雅可比行列式平均值为0.896 5。从图6可以看出，经过HSCR优化后的形变结果的雅可比行列式的值更加靠近1，这表明增加控制点后得到的形变比初始形变更加平滑。且改善了形变的体保持特性。

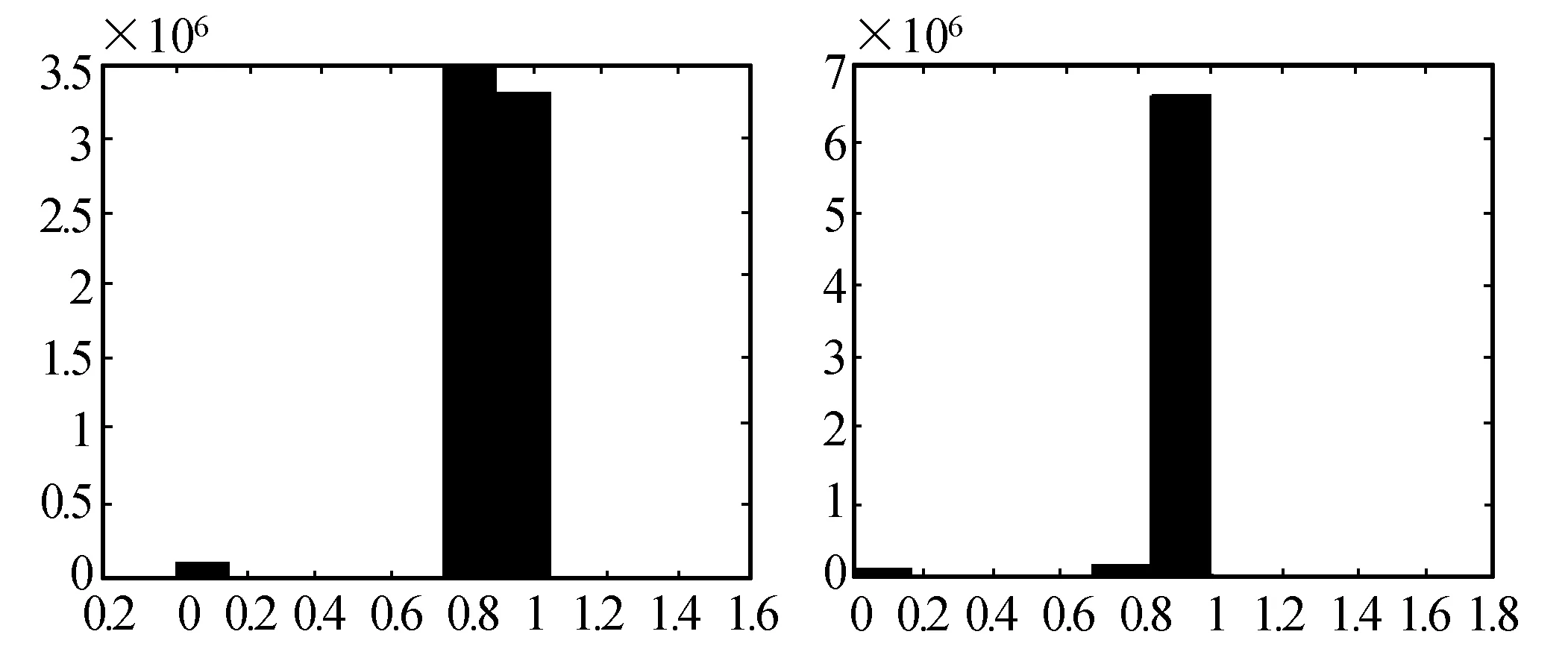
(a) 初始控制点得到的形变的雅可比行列式统计直方图 (b) 增加控制点后的雅可比行列式统计直方图图6 增加控制点前后配准结果得到的雅可比直方图统计对比

3 结 语

为了得到连续、平滑且满足一致性形变约束的肺形变模型，本文针对4DCT图像提出了时空一致性配准方法。该方法提取初始点集，利用SEST算法对点集进行跟踪，并从形变图像和目标图像尽可能相似，形变扭曲尽可能小，控制点轨迹尽可能平滑，以及正反形变之间满足一致性约束等方面，提出了一个优化模型，对提取的控制点进行优化调整。采用层次时空一致性配准策略，逐层增加新的控制点集，并通过优化模型对控制点进行调整，以提高配准精度。降低正反向形变的一致性误差。在DIR-lab数据库中测试了算法性能，实验结果表明，该配准方法可以达到良好的配准精度，同时可以保证形变的平滑度和一致性，并改善了形变的体保持特性。

[1] Tan C, Yi J B, Yang X. Transformation models for four-dimensional image registration: A survey [J]. Recent Patents and Topics on Imaging, 2015, 5: 88-96.

[2] Johnson H J, Christensen G E. Consistent landmark and intensity-based image registration [J]. IEEE Transactions on Medical Imaging, 2002, 21(5): 450-461.

[3] Bookstein F L. Principal warps: Thin-plate splines and the decomposition of deformations [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(6): 567-585.

[4] Castillo E, Castillo R, Martinez J,et al. Four-dimensional deformable image registration using trajectory modeling[J]. Physics in Medicine and Biology, 2010, 55(1): 305-327.

[5] Sotiras A, Davatzikos C, Paragios N. Deformable medical image registration: A Survey [J]. IEEE Transactions on Medical Imaging, 2013, 32(7): 1153-1190.

[6] Zhang Z, Jiang Y, Tsui H. Consistent multi-modal non-rigid registration based on a variational approach [J]. Pattern Recognition Letter, 2006, 27(7): 715-725.

[7] Alvarez L, Deriche R., Papadopoulo T, et al. Symmetrical dense optical flow estimation with occlusions detection [J]. Lecture Notes in Computer Science, 2002, 2350: 721-735.

[8] Ye X, Chen Y. A new algorithm for inverse consistent image registration [J]. Advances in Visual Computing, 2009, 5875: 855-864.

[9] Leow A, Huang S, Geng A, et al. Inverse consistent mapping in 3D deformable image registration: Its construction and statistical properties [J]. Information Processing in Medical Imaging, 2005, 3565: 493-503.

[10] Modat M, Cardoso M J, Daga P, et al. Inverse-consistent symmetric free form deformation [J]. Information Processing in Medical Imaging, 2013, 4765: 323-329.

[11] Christensen G E, Rabbitt R D, Miller M I. Deformable templates using large deformation kinematics [J]. IEEE Transactions on Image Processing, 1996, 5(10): 1435-1447.

[12] Yang X, Zhang D, Yao S, et al. A fast algorithm to estimate inverse consistent image transformation based on corresponding landmarks[J]. Computerized Medical Imaging & Graphics the Official Journal of the Computerized Medical Imaging Society, 2015, 45:84-98.

[13] Shen D, Davatzikos C. HAMMER: Hierarchical attribute matching mechanism for elastic registration [J]. IEEE Transactions on Medical Imaging, 2002, 21(11): 1421-1439.

[14] Wu J H, Hu B F, Yang X. Deformable registration of 4D-CT image using landmark tracking [J]. Biomedical Research, 2016, 27(2): 797-807.

[15] Baboiu D M, Hamarneh G. Vascular bifurcation detection in scale-space[C]// Mathematical Methods in Biomedical Image Analysis (MMBIA), 2012 IEEE Workshop on. IEEE, 2012: 41-46.

[16] www.dir-lab.com.

[17] Yang X, Pei J. Lung deformation estimation using spatially mean shift for 4D-CT[C]// IEEE International Conference on Bioinformatics and Biomedicine. IEEE, 2013:237-242.

[18] Metz C T, Klein S, Schaap M, et al. Nonrigid registration of dynamic medical imaging data using nD+ t B-splines and a groupwise optimization approach [J]. Medical Image Analysis, 2011, 15(2): 238-249.

[19] Wu G, Wang Q, Lian J, et al. Reconstruction of 4D-CT from a Single Free-Breathing 3D-CT by Spatial-Temporal Image Registration[M]// Information Processing in Medical Imaging. Springer Berlin Heidelberg, 2011:686-698.

CONSISTENTREGISTRATIONMETHODFORTHEMULTILAYERSPATIO-TEMPORAL4DCTLUNGIMAGES

Yang Hao1Hu Bingfeng2Sun Ruifang2Yang Xuan2*1

(Xi’anElectricPowerCollege,Xi’an710032,Shaanxi,China)2(CollegeofComputerScienceandSoftware,ShenzhenUniversity,Shenzhen510086,Guangdong,China)

Four-dimensional CT lung images provide lung dynamic information, which can be widely used in the diagnosis of pulmonary diseases and precise radiotherapy. This paper proposes a hierarchic spatio-temporal consistent registration for 4D CT lung images. The proposed method extracts control points from the image at the maximum inhalation phase, and tracks these control points by using the structure tensor tracking algorithm; a hierarchical spatio-temporal consistent optimization model is proposed to adjust the control points finely, which has the advantages of improvement of the registration accuracy as a whole; new control points are selected from the region where consistent errors are large, and are added to the control point set after each optimization. These newly added control points are optimized further to reduce the consistent errors of registration. In the proposed method, the spatial smoothness constraint keeps the deformation smooth; the temporal smoothness constraint keeps the trajectories of points stable; the consistent constraint reduces the consistent errors introduced by the transformations in two directions. The experimental results of public dataset show that the proposed method can estimate smooth, stable, and reasonable deformation results.

Image registration CT images Consistent transformations Spatio-temporal constraints

TP391

A

10.3969/j.issn.1000-386x.2017.09.040

2016-09-16。国家自然科学基金联合项目(U1301251)。杨浩，讲师，主研领域：医学图像处理。胡冰锋，硕士。孙瑞芳，硕士生。杨烜,教授。