基于标定场的激光雷达两步标定方法*

吴奋陟，郭绍刚，朱飞虎，王 立，吴 云，刘 达

(北京控制工程研究所,北京 100190)

基于标定场的激光雷达两步标定方法*

吴奋陟，郭绍刚，朱飞虎，王 立，吴 云，刘 达

(北京控制工程研究所,北京 100190)

针对激光雷达大测量范围高精度测角测距问题，提出一种基于标定场的激光雷达两步标定方法.该方法在分析激光雷达测角误差和测距误差的基础上，提出激光雷达误差修正模型.该模型将距离修正从标定模型中分离，首先利用靶标场完成全视场的角度标定，并确定其外部参数，再利用基线场实现距离标定.以降低距离标定参数与角度标定参数之间的耦合性，保证激光雷达角度和距离标定的精度和准确度.实验结果表明方法合理有效，能够实现激光雷达的高精度标定.

激光雷达；两步标定；标定场

0 引 言

激光雷达是以发射激光束探测目标距离、方位、速度等信息的雷达系统.由于其测量速度快、精度高、抗干扰能力强、测量范围广、获取信息直观、数据量大等，成为空间探测和感知必备的测量敏感器.

激光雷达标定的目的在于修正其测距和测角误差等内部参数，确定其测量本体坐标系的位置和指向，即外部参数.标定参数的确定是激光雷达高精度测量的前提.传统标定方法一般根据约束关系直接对所有标定参数进行最优估计；为了保证标定精度，通常采用特制的标志物，以建立严格的约束方程.项志宇等[1]将一定宽度的木棍放置在已知距离上，通过建立已知距离与激光雷达测量值、初始姿态偏差和系统偏心误差的关系，标定解算系统参数.胡少兴等[2]将5块平面板放置在激光雷达各个轴向的已知距离上，作为测量点在某个轴向上的理论坐标，用于修正系统中心偏差、测距误差和安装姿态误差等参数.Andreas Rietdorf等[3-4]采用若干平面度好的平板标定三维成像激光雷达，根据平面特征约束建立条件方程，并利用Gauss-Helmert 模型方法得到激光雷达内部参数的最优估计值.Yuriy Reshetyuk等[5-7]在室内或室外布置一定数量的目标，将目标理论位置与激光雷达测量值一一对应建立约束方程，同时解算系统的内、外参数.上述方法要求采用特制的标志物，利用约束关系同时求解3～5个修正参数，难以满足激光雷达高精度标定的需要.

本文提出一种基于标定场的激光雷达两步标定方法.所需标定场简单、易实现，便于重复使用，对标定装置平面度要求低.采用的标定模型将距离修正从完整模型中分离，首先利用靶标场完成角度标定，并确定其外部参数，再利用基线场实现距离标定.该方法使众多标定参数得到了一定程度的分离，降低了距离标定参数与角度标定参数之间的耦合性，保证了激光雷达角度和距离标定的精度和准确度.

1 激光雷达工作原理

本文所述激光雷达通过电机带动两个转轴互相垂直的摆镜高速旋转，将激光束出射至被测目标，分别根据激光束的飞行时间、两个正交方向的电机转动角度，测量得到被测目标的距离大小R和方位(β,α)，从而完成极坐标式的点位测量，如图1所示.

激光雷达的光路折转由安装在转轴正交电机XM和YM上的水平摆镜和垂直摆镜实现.激光器出光后入射至水平摆镜(X摆镜)，X摆镜在一定角度范围内转动将入射至该摆镜的光线以不同角度折转至垂直摆镜(Y摆镜)，Y摆镜转动使得光线以不同角度折转出射并入射至目标(如图4)；进入光学系统入瞳的光线可以认为是平行出射光经过扫描机构两路摆镜原路返回光学系统.

2 误差修正模型

2.1测角误差分析

影响激光雷达角度测量精度的主要因素有：

1)电机测角误差，是指由于角度位置检测器件性能等因素导致的电机测角单元的测量误差；该误差直接影响水平角和垂直角的测量精度.

2)激光入射不垂直误差，是指由于整机装配不理想导致激光入射方向与X摆镜旋转轴不垂直的误差.

3)水平轴与垂直轴不垂直误差，是指由于整机装配不理想导致的实际水平轴和垂直轴偏离理想状态，使得两旋转轴不正交.

4)摆镜不垂直误差，是指由于摆镜自身面形缺陷以及安装偏差等因素导致的摆镜法线与各自旋转轴的不垂直误差.

2.2测距误差分析

激光雷达采用基于飞行时间的距离测量原理.影响距离测量精度的主要因素有：

1)时间基准误差，是指由于时间测量芯片的时间分辨率导致的距离测量误差.

2)上升沿抖动误差，是指由于数字电路的上升沿抖动导致时间测量出现偏差.

3)前沿鉴别误差，是指由于激光脉冲宽度、信噪比、衰减系数等因素导致时间测量电路的时间鉴别存在误差.

4)零位误差，是指距离测量电子零和机械零的偏差.电子零是指电子线路开始参考脉冲计数的原点；机械零是指机械结构上光路出射的原点.

5)回波强度误差，是指回波信号强度影响时间测量精度.

6)大气折射率误差，是指大气折射率影响光传播的速度，从而导致距离测量存在误差.

2.3测角误差修正模型

激光雷达与全站仪均为极坐标式的测量，尽管两者的结构组成和机械形式不同，但轴系关系相同.因此激光雷达角度修正借鉴成熟的全站仪轴系误差修正模型[8].该模型能够减弱轴系误差对角度测量的影响，修正了由于测角单元误差、装配误差等因素引起的水平角测量与垂直角测量的相关性.

(1)垂直角β修正

垂直角β测量误差通过引入垂直角比例系数q和常系数w进行修正：

β′=β+qβ+w

(1)

其中，β′为修正后的垂直角.

(2)水平角α修正

水平角α测量误差通过全站仪误差模型中的视准轴误差修正系数e和水平轴误差修正系数c进行修正：

(2)

其中，α′为修正后的水平角.

(3)完整的角度修正模型

激光雷达按照极坐标方式测量目标点的空间位置，输出距离R、垂直角β和水平角α.不考虑测量误差，目标点在世界坐标系下的笛卡尔坐标为

(3)

其中，(X,Y,Z)为目标在世界坐标系下的三维坐标的理论值，(Tx,Ty,Tz)为激光雷达测量本体系原点在世界坐标系下的坐标.考虑测距和测角误差，Rw(φx,φy,φz)为激光雷达测量本体系至世界坐标系的旋转阵；引入如式(1)、(2)所示的角度误差修正模型，同时将目标点在世界坐标系下的笛卡尔坐标转为极坐标形式，得到与距离无关的角度及外参数修正模型，如下所示：

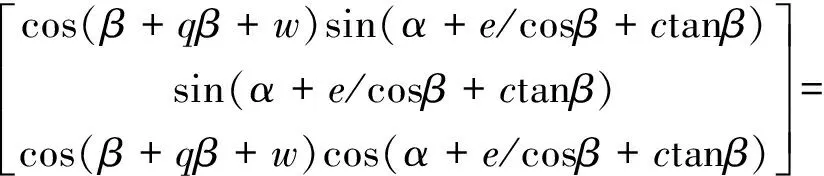
(4)

(5)

(6)

(7)

(8)

2.4测距误差修正模型

根据基于飞行时间的测距原理，时间t内测量距离R为

(9)

式中，t为测量的时间间隔，c为光在真空中传播的速度，n为大气折射率，N为记录的脉冲个数，T0为脉冲宽度.

根据误差传播定律，对式(9)求全微分：

(10)

(11)

其中，R表示未修正的距离测量值.

考虑时间延迟和零误差的影响，激光脉冲式测距存在固定的距离测量误差v，通常称为测距加常数[9].

因此，综合考虑，激光雷达的距离测量值按照式(12)进行修正

R′=R+kR+v

(12)

其中，R表示激光雷达输出的距离测量值，R′表示经过修正系数k和v修正后的距离测量值.

2.5最优化求解

将每一个空间点的测量值与理论值作为已知值，根据式(4)～(8)可得：

(13)

(14)

式(14)中，Fk=F(Pk)为初值Pk处的函数值；Jk=J(Pk)为初值Pk处F(Pk)的雅克比矩阵；μk为阻尼因子.采用该方法对标定参数进行最优估计，收敛速度快，精度高[11].

将距离测量值与理论值作为已知值按照式(12)对应，可得：

(15)

每个空间点可列1个方程，则n个点有n个方程，待求未知数(k,v)两个；当已知点不少于2个时，采用最小二乘法求解，如下所示：

(16)

(17)

3 标定试验

表1 激光雷达标定内参数Tab.1 Intrinsic parameters of lidar

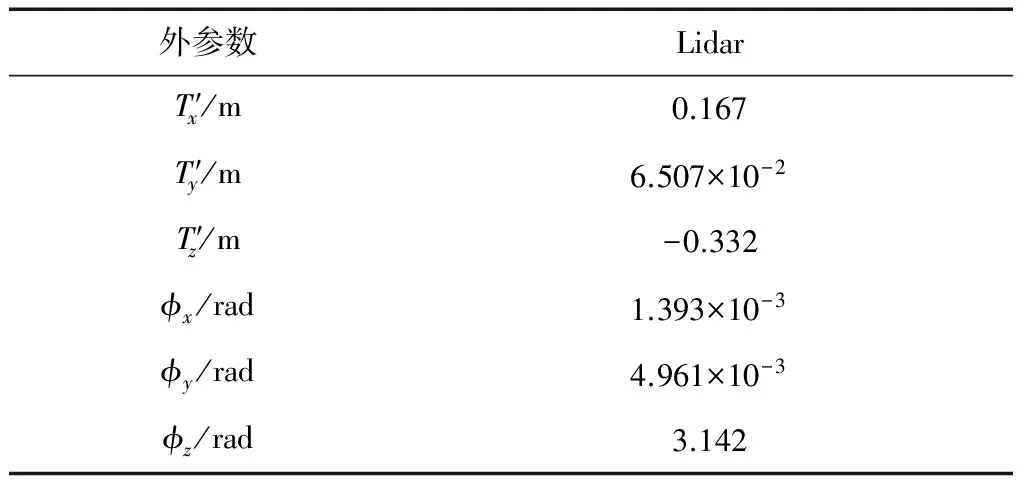
表2 激光雷达标定外参数Tab.2 External parameters of lidar

在实验室70 m范围内，对激光雷达的角度和距离标定精度进行了验证.在30°×30°视场范围内共计选取了10个角度位置验证激光雷达标定后的测角精度.验证结果如图6～7所示.另外，选取了11段距离验证激光雷达标定后的测距精度.验证结果如图8所示.

在室内70 m范围内，激光雷达30°×30°视场标定精度优于0.007°(3σ)，距离精度优于0.1 m(3σ).

4 结 论

本文在分析激光雷达测角误差和测距误差的基础上，提出一种误差修正模型，该模型将距离修正从标定模型中分离，首先利用靶标场完成角度标定，并确定其外部参数，其次利用基线场实现距离标定.该方法使众多标定参数得到了一定程度的分离，降低了距离标定参数与角度标定参数之间的耦合性，保证了激光雷达角度和距离标定的精度和准确度.方法基于标定场实现，对标定装置平面度要求低，简单易于实现.实验结果表明，该方法能够有效修正激光雷达的测距和测角误差，标定后角度测量精度优于0.007°(3σ)，距离测量精度优于0.1 m(3σ)，方法可用于激光雷达敏感器的高精度标定.

[1] 项志宇. 快速三维扫描激光雷达的设计及其系统标定[J]. 浙江大学学报(工学版)，2006,40(12)：2130-2133. XIANG Z Y.Fast 3D Scanning laser radar system design and calibration[J]. Journal Of Zhejiang University(Engineering Science), 2006,40(12)：2130-2133.

[2] 胡少兴，张爱武，刘海云，等. 360°连续扫描的便携式三维激光雷达设计与开发[J]. 光学学报，2008,28(s1)：168-171. HU S X, ZHANG A W,LIU H Y.Designing and developing a360°continuous scanning portable 3D lidar system[J]. Acta Optica Sinica, 2008,28(s1)：168-171.

[3] ANDREAS R, FRANK G, JENS A. A concept for the calibration of terrestrial laser scanners[C]//Proceedings FIG Working Week. Athens, 2004.

[4] 郁肖飞，史朝龙，李新纯，等. 多光束三维成像激光扫描系统校准方法研究[J]. 战术导弹技术，2013,2:92-98,113. YU X F, SHI C L, LI X C. Study of calibration of the multi-beam 3D imaging laser Scanners[J]. Tactical Missile Technology, 2013,2:92-98,113.

[5] YURIY R. Investigation and calibration of pulsed time-of-flight terrestrial laser scanners[D]. Stockholm:Royal Institute of Technology,2006.

[6] 陈玮娴，陈义，袁庆. 地面三维激光扫描仪的自检校场布设方案研究[C]//大地测量学术年会暨第六届全国大地测量研究生学术论坛.淄博，2011. CHEN W X, CHEN Y, YUAN Q.Study on self calibration field layout scheme of ground 3D laser scanner[C]//Annual Conference on Geodesy and The 6thNational Symposium on Geodesy Postgraduates. Zibo, 2011.

[7] 高宝华，蒋理兴，郭连惠，等. 地面三维激光扫描仪自检校方法研究[J]. 海洋测绘，2012,32(5)：45-52. GAO B H,JIANG L X, GUO L H. Study on the self-calibration method of the laser scanner[J]. Hydrographic Surveying and Charting, 2012,32(5)：45-52.

[8] 徐忠阳. 全站仪轴系误差自动修正及其对角度观测的影响[C]//全国测绘仪器综合学术年会，北京，中国测绘学会，2003. XU Z Y.Automatic correction of shafting error of total station and Influence on angle observation[C]//National Comprehensive Academic Annual Meeting of Surveying Instruments. Beijing, Chinese Society for Geodesy, Photogrammetry and Cartography, 2003.

[9] 耿春萍，程度，张治. 激光脉冲测距的测距精度及误差分析[J]. 光电技术应用，2007,22(2)：28-31. GENG C P, CHENG D, ZHANG Z. Precision and error analysis of laser pulse ranging[J]. Electro-Optic Technology Application. 2007,22(2)：28-31.

[10] 李庆扬. 数值计算原理[M]. 北京: 清华大学出版社, 2000:291-295.

[11] Leica Geosystems AG. TM6100A User Manual

Two-StepCalibrationMethodofLidarSensorBasedonCalibrationField

WU Fenzhi, GUO Shaogang, ZHU Feihu, WANG Li, WU Yun, LIU Da

(BeijingInstituteofControlEngineering,Beijing100090，China)

In order to solve the problem of high precision distance and angle measurement of lidar with large measurement range, a two-step calibration method of lidar sensor based on calibration field is proposed in this paper. Based on the analysis of the angle measurement error and the distance measurement error of lidar, an error correction model is proposed in this paper. This model separates the distance correction from the angle correction. First, the calibration field is used to complete the angle calibration, and the external parameters are also calculated in this step. Second, the baseline field is used to complete the distance calibration. This method reduces the correlation between the distance calibration parameters and the angle calibration parameters, and guarantees the calibration precision and accuracy. The experimental results show that the method is reasonable and effective, and is able to complete the high precision calibration of lidar.

lidar; two-step calibration; calibration field

TP391

：A

： 1674-1579(2017)04-0057-06

10.3969/j.issn.1674-1579.2017.04.010

*国家重点基础研究发展计划(973)资助项目(2013CB733100).

2017-04-18

吴奋陟(1986—)，女，工程师，研究方向为成像式敏感器标定；郭绍刚(1982—)，男，高工，研究方向为成像式敏感器方案设计；朱飞虎(1986—)，男，高级工程师，研究方向为成像式敏感器电路设计；王立(1976—)，男，研究员，研究方向为成像式敏感器方案设计；吴云(1985—)，男，工程师，研究方向为三维点云处理算法设计；刘达(1980—)，男，高级工程师，研究方向为成像式敏感器算法设计.