基于并行度最大化的多目标优化任务划分算法

袁开坚，张兴明，高彦钊

(国家数字交换系统工程技术研究中心，郑州 450002) (*通信作者电子邮箱kaijian_yuan@163.com)

基于并行度最大化的多目标优化任务划分算法

袁开坚*，张兴明，高彦钊

(国家数字交换系统工程技术研究中心，郑州 450002) (*通信作者电子邮箱kaijian_yuan@163.com)

针对可重构系统硬件任务划分并行度最大问题，提出一种基于并行度最大的多目标优化任务划分算法。首先，该算法在满足可重构硬件面积资源和合理依赖关系的约束下，按广度优先的遍历方式搜索待划分的操作节点；然后，着重考虑执行延迟对于系统完成时间的影响，将块内操作节点的并行度最大化；最后，在减少碎片面积和不增加块间连接边数的原则下接受新的节点，否则就结束一个块划分。实验结果表明，与现有的基于层划分(LBP)和基于簇划分(CBP)两种算法相比，提出的算法获得了最大的块内操作并行度，同时还减少了划分块数和块间的连接边数。

可重构系统；任务划分；并行度最大化；多目标优化；广度优先搜索

0 引言

现如今随着可编程逻辑器件的快速发展，可重构计算(Reconfigurable Computing, RC)成为了一种新的计算方式[1]，这种方式可以通过软件配置结构可变的硬件，故其既具备了软件的通用性、灵活性，又兼具了专用集成电路(Application Specific Integrated Circuit, ASIC)的高性能低功耗的优点。可重构计算凭借其优越性在解决数字信号处理[2]、多媒体处理[3]、加解密算法[4]等资源密集型计算上，成为了一种理想的选择。

在可重构计算的任务编译过程中，由核心循环转换来的数据流图(Data Flow Graph, DFG)如何被映射到可重构处理单元(Reconfigurable Processing Unit, RPU)是实现可重构系统高性能的关键所在[5]。其中转换来的数据流图的节点表示计算任务，如加法、减法、乘法等，有向边表示节点之间的数据依赖关系[6]。对于一个计算密集型应用而言，需要的硬件资源往往大于可重构处理单元所能提供的资源。此时需要对任务划分成若干个子任务，分时复用处理单元上提供的硬件资源，这个过程叫作任务的时域划分[7]。

可重构计算硬件任务的时域划分问题实质就是图的分割问题，已经被证明是一个NP完全问题[8-9]。目前的研究在并行度、块间通信量、划分块数等影响因素中，往往追求其中一个最优解，而忽略了其他因素的优化对系统的影响[10]。文献[11]首次针对可重构计算提出了两种任务划分的方法，层划分和簇划分。基于层划分(Level Based Partitioning, LBP)是采用ASAP(As Soon As Possible)策略分层，根据贪心算法来提高各个划分块中节点的并行度，但忽略了操作节点之间的依赖关系，造成划分块之间的通信量增大，并且还产生大量硬件碎片。基于簇的划分(Cluster Based Partitioning, CBP)是基于列表的启发式算法，将数据依赖关系紧密的操作尽可能地划分到同一个块中，以减少划分块之间的通信量，复杂度较低，但是仍然会产生大量的碎片。这两种方法都是针对单一目标的算法，并没有统筹考虑多个因素的影响。文献[12]针对簇划分产生面积碎片问题改进，充分利用硬件面积资源减少了划分块数，但又忽略了块间的通信量。文献[13]提出了一种划分块数最小化的硬件任务划分算法，还考虑了执行总延迟、划分块之间边数等多个因素，有效地减少了可重构系统的配置时间，但随着RPU增大，划分块间的边数增加，延长了通信延迟。文献[14-15]利用基因算法虽然获得较好的划分结果，但是以牺牲执行延迟为代价，不能很好地满足可重构系统的快速划分要求。文献[16]提出了一种并行度最大化的贪婪算法，获得较大并行度，但此算法假设资源没有限制，并没有考虑实际存在的硬件碎片问题。

本文针对执行延迟最小化的任务划分需求，提出了一种基于并行度最大化的多目标优化(Parallelism Maximization with Multi-objective Optimization, PMMO)可重构任务划分算法。采用广度优先的遍历方式，在保证任务划分获得最大的块内并行度下，采取了多种划分策略，提高资源面积的利用率，综合优化了划分块数和块间通信量等因素的影响，在实现并行最大的同时达到一种多目标优化的效果。

1 模型的描述与定义

为了研究任务划分问题，这里给出数据流图和划分问题相关的形式化模型定义。

定义1 一个数据流图可以用G=(V,E,S,L)来表示。节点vi∈V(1≤i≤n)表示某一具体的运算操作符，有向边eij=〈vi,vj〉,eij∈E表示节点vi与vj存在依赖关系，vi是vj先驱节点，vj是vi的后继节点。在操作符vj运算之前，操作符vi必须要先完成运算。当每一个运算符映射到可重构处理单元上时，都要有相应的所需资源面积和执行延迟。用si∈S来表示节点vi的硬件资源面积，SRPU表示一块可重构处理单元的面积。用li∈L来表示节点vi的执行延迟。

定义2 采用某种划分方法可以得到一种具有k个模块的划分,表示为P={p1,p2,…,pk}。其中第i个划分块pi由任务中的若干个节点组成。

定义3 一个任务节点vi被划分到某一模块时，其所有前驱节点必须已经划分到已完成执行的模块中，否则就会产生不合理的依赖关系。当两个划分模块之间存在着不合理的依赖关系，就是一个不合理的划分。图1给出了一种划分示例。假设每一个节点操作所需资源相同，即可以用节点数表示所需面积资源。设SRPU=2，限定图1(a)的每一个划分块的节点数不能超过2。图1(b)中的划分块p2中的有一个节点的前驱节点在p3中，同时划分块p3中的有一个节点的前驱节点也在p2中。无论是按照p1p2p3的顺序执行，还是按照p1p3p2的顺序执行，p2和p3之间都产生了不合理的依赖关系，此划分是一个不合理的划分。而图1(c)中的划分块之间都满足依赖关系，是一个合理的划分，可以按照p1p2p3的顺序执行。

定义4 设Bi是可重构系统对划分模块pi配置的时间，Ci是pi与其他模块进行数据通信的时间，Di是模块pi内部节点的执行延迟。设划分成k个模块的一个任务在系统中执行所需的总时间记为：

(1)

由式(1)可知，为了使执行总时间最少，就要使模块的配置时间、模块间的通信时间、模块内的执行延迟最小，对应地就要减少划分的模块数、减少模块间的连接边数、增大模块内部节点的执行并行性。

图1 划分示例

定义5 一个可重构系统的时域划分模型可以描述如下。

输入：G=(V,E,S,L)，SRPU。

输出：一种划分P={p1,p2,…,pk}。

约束条件：

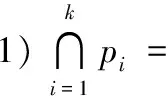
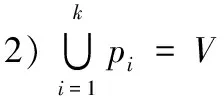
4)待划分节点的所有前驱节点必须已经划分到已完成执行的模块中。

目标：1)执行并行度最大化；2)划分的块数较小化；3)尽可能减少划分块之间的连接边数。

2 算法设计及分析

2.1 PMMO算法设计

为了保证一个DFG的任务划分获得最小的执行延迟，尽量减少划分块数与块之间的连接边数，PMMO算法在满足RPU硬件面积资源和合理依赖关系的约束下，按广度优先的遍历方式，着重考虑了执行延迟对于系统完成时间的影响，最大化划分块内的并行性，并且优化了资源面积的利用。PMMO算法采取以下策略来进行算法设计。

策略1 保证划分块内的操作并行度最大化。

在满足资源面积和依赖关系的前提下，采用广度优先的原则，优先选择当前层的操作节点进行划分。当遇到不能满足约束条件的节点时跳过，继续查找其后处于就绪状态的节点，当遍历搜索到了满足条件的节点时，还要考虑加入此节点之后的块内执行延迟不能大于当前的块内延迟，这样才能将节点添加到当前的划分块中。当本层的就绪节点搜索完毕时，接着优先考虑所属层号较小的就绪节点。此策略的目的就是使块内操作并行最大化，从而使整个任务的执行延迟最小化。

策略2 在保证策略1的情况下，充分利用可重构处理单元的面积资源。

当有多个节点处于就绪状态且执行延迟相同时，在保证合理划分的要求下，优先选择占用硬件面积资源大的操作节点，使得剩余硬件碎片较小，提高资源的利用率。此外对于队首之后的节点，在满足剩余硬件资源碎片和不增加执行延迟的条件下，贪婪搜索可以将其加入到当前块中，进一步减少硬件碎片。此策略的目的是在块内操作并行性最大化下，充分利用处理单元面积资源，减少硬件碎片，尽可能减少划分的块数。

策略3 在保证策略1的情况下，尽量减少划分块之间的连接边数。

每次将一个节点划分到块中，都要更新当前划分块与就绪节点之间的连接边数，边数越多说明节点与划分块联系越紧密，在满足执行延迟的条件下，尽可能将其划入到块中。此外当有多个就绪节点都满足约束要求时且加入节点后块间的连接边数不大于当前的边数时，优先选择当前块内的后继节点，这样可以使紧密型的操作节点更多地处于同一划分块中。此策略的目的是在操作并行性最大化下，减少划分块之间的边数，降低块间的通信时间。

基于以上3个策略，PMMO算法描述如下。

输入：一个任务的DFG。 输出：一个划分后的DFG、所有划分块的执行延迟总和、划分块数、块间的连接边数总和。 约束：SRPU、待划分节点的所有前驱节点必须已经划分到已完成执行的模块中。 init();

//初始化节点

level();

//计算每个节点所在层

ready_list();

//就绪节点列表

采用广度优先遍历；

while(rList!=NULL) if

((Area_Used+node[vi].area)<=SRPU) 更新使用面积； 更新块间的边数； 更新块内的延迟； quickSort();

//选择所属层号较小的节点 End if;

if

((area_used+node[vi].area)>SRPU) 跳过该点，搜索后面满足条件的节点； End if;

End while;

while(pList!=NULL) if ((area_used+node[vi].area)<=SRPU)quickSort();

//选择满足条件且所用面积最大的节点 分别计算当前块和加入新节点之后的边数和延迟；if(edges_delt<=0 && delays_delt<=0) 将该点加入块中，优先选择当前块内的后继节点； End if;

End if;

End while;

得出划分块数;

cal_edges();

//求出划分块间的连接边数

cal_delays();

//求出划分块执行延迟总和

2.2 算法时间复杂度分析

对于一个n个节点的DFG，已知每个运算节点的类型、执行延迟和所用资源数。时间复杂度主要分析算法中使用的函数，初始阶段的init()、level()、ready_list()，过程中的quickSort()，结束阶段的cal_edges()、cal_delays()，综合分析这些函数即可得到整个算法的时间复杂度。

初始化函数init()求得每个节点入度和出度个数、前驱与后继列表，该函数的时间复杂度为O(n2)。level()求得每个运算节点层数，时间复杂度为O(n2)。ready_list()就绪节点列表实现过程是对每个操作节点，考察它的所有前驱节点，如果所有的前驱都已经过划分被分配到相应模块中，就将此节点加入列表，时间复杂度为O(n)。

当节点未被划分完全时，要对待划分节点重新排序,每次通过快速排序quickSort()求出所属层号较小的节点和可以划入当前块占用硬件资源最大的节点。大家知道快速排序算法最坏情况下的时间复杂度为O(n2)，又因为运用到快速排序是在节点未被划分完全时，所以是在一层循环下O(n)进行的，因此该处理过程的时间复杂度为O(n3)。

cal_edges()通过扫描n个运算节点及其后继列表来求出划分块间的连接边数总和,其时间复杂度为O(n2)；假设一个任务DFG被划分为k块，函数cal_delays()用递归调用求得划分后所有块执行总延迟，时间复杂度为O(n·k)。综上，PMMO算法的时间复杂度约为O(n3)。

3 实验及结果分析

3.1 实验设计

采用C语言实现算法，并且与两种效果较好的单一目标算法LBP、CBP作对比。为了便于实验对比，本文采用了文献[13]相同的几类操作运算所占用的硬件资源数(单位用可配置逻辑模块(Configurable Logic Block， CLB)个数表示)和时钟周期数，即加法、减法、乘法所占的硬件面积资源分别为5 CLB、13 CLB、27 CLB，时钟周期分别为1，1，2。

本文从数字信号处理领域选取了6种常用的标准程序集用来验证划分算法，分别是基- 4、基- 8、基- 16快速傅里叶变换，8×8离散余弦变换，4阶矩阵乘法，6×6快速离散余弦变换，所用操作单元数量如表1所示，操作单元总数依次增加。实验硬件环境为Intel Core i3 CPU,2.53 GHz,RAM 4 GB的笔记本电脑，程序运行环境为Windows 7。SRPU随机选取54 CLB、67 CLB、78 CLB。

表1 划分基准程序集

3.2 算法比较

3.2.1 PMMO算法与LBP算法比较

PMMO算法与LBP算法的划分结果对比数据见表2，其中：D代表执行延迟时钟周期数，B代表划分块数，E代表块间的连接边数。相比LBP算法，在SRPU为54 CLB时PMMO算法对于执行延迟平均减少10.3%，对于划分块数平均减少12.1%，对于块间连接边数平均减少4.6%。在SRPU为67 CLB时PMMO算法对于执行延迟平均减少13.1%，对于划分块数平均减少13.7%，对于块间连接边数平均减少7.5%。在SRPU为78 CLB时PMMO算法对于执行延迟平均减少17.4%，对于划分块数平均减少15.3%，对于块间连接边数平均减少10.8%。将以上说明的在不同可重构硬件资源下各参数的平均减少率整合在图2中。LBP算法是减少执行延迟较为有效的算法，而提出的PMMO算法在执行延迟方面进一步改进，获得了较大的操作并行度，并且对于划分块数和连接边数也有明显的减少，具有较好的划分性能。

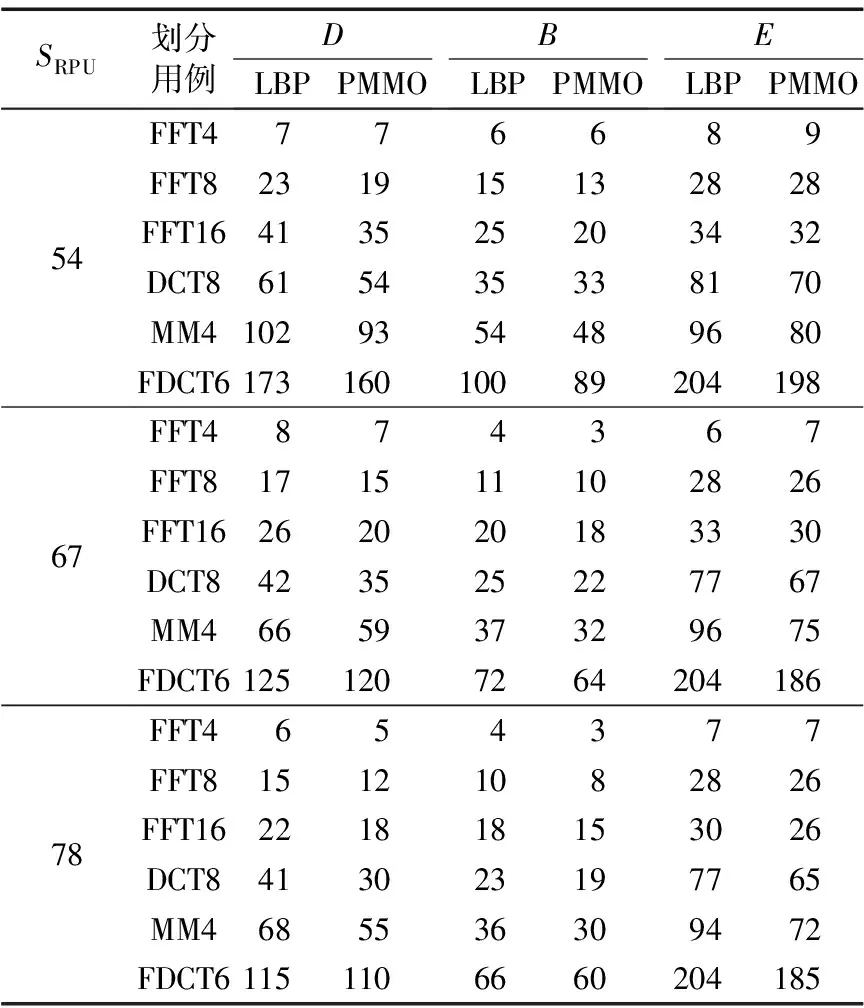
表2 不同SRPU值时LBP与PMMO划分结果对比

图2 相比LBP各指标的平均减少率

3.2.2 PMMO算法与CBP算法比较

PMMO算法与CBP算法的划分结果对比数据见表3。相比CBP算法，在SRPU为54 CLB时PMMO算法对于执行延迟平均减少25.3%，对于划分块数平均减少14.1%，对于连接边数平均减少1.2%。在SRPU为67 CLB时PMMO算法对于执行延迟平均减少26.5%，对于划分块数平均减少10.8%，对于连接边数平均减少1.7%。在SRPU为78 CLB时PMMO算法对于执行延迟平均减少28.2%，对于划分块数平均减少13.1%，对于连接边数平均减少2.5%。将以上说明的在不同可重构硬件资源下各参数的平均减少量整合在图3中。在执行延迟和划分块数方面相比CBP算法，提出的算法均有显著改善，但由于CBP是减少块间通信量的较好的算法，所以对于连接边数的改进不是非常明显。

通过以上实验对比结果可以看出，PMMO算法相比LBP、CBP算法，对于减少执行延迟有显著的效果，对于减少划分块数也有明显的效果，因为LBP、CBP算法一遇到不满足的节点就结束一个块的划分，而PMMO则采用贪婪策略，搜索到更多的节点划分到块中，尽可能地减少划分块数。然而在保证块内并行度最大和较少的划分块数的情况下，再降低块间通信量的空间就较为有限，因而算法的块间通信量的降低幅度小于其他两种目标参数的改进幅度。并且通过图2～3可以看出，相比LBP、CBP，提出的算法在总的可重构硬件资源数增加时，执行延迟、划分块数和连接边数的平均减少率都有所提高，这说明PMMO算法在硬件资源较大时，表现出的划分性能更好，所以更适用于大数据量应用的任务划分场景。

表3 不同SRPU值时CBP与PMMO划分结果对比

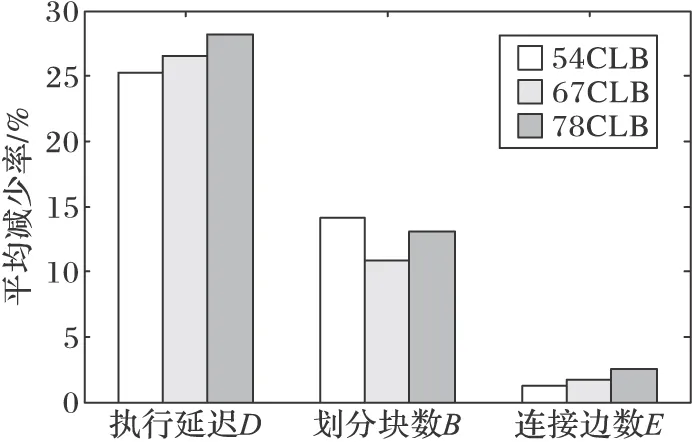
图3 相比CBP各指标的平均减少率

4 结语

本文针对可重构任务划分问题，提出了一种PMMO算法。该算法采用广度优先的遍历方式，综合考虑多种影响因素，采取了多种划分策略，利用数字信号处理领域标准程序集转化来的DFG进行实验，与LBP、CBP算法比较，获得了最大的块内操作并行度，同时还能减少划分块数和块间连接边数，得到的划分结果具有明显改善。

References)

[1] DEHON A. Fundamental underpinnings of reconfigurable computing architectures [J]. Proceedings of the IEEE, 2015, 103(3): 355-378.

[2] ROSSI D, CAMPI F, DELEDDA A, et al. A heterogeneous digital signal processor implementation for dynamically reconfigurable computing [C]// CICC ’09: Proceedings of the 2009 Custom Integrated Circuits Conference. Piscataway, NJ: IEEE, 2009: 641-644.

[3] GENG T, LIU L, YIN S, et al. Parallelization of computing-intensive tasks of the H.264 high profile decoding algorithm on a reconfigurable multimedia system [J]. IEICE Transactions on Information & Systems, 2010, 93-D(12): 3223-3231.

[4] 陈韬,罗兴国,李校南,等.一种基于流处理框架的可重构分簇式分组密码处理结构模型[J].电子与信息学报,2014,36(12):3027-3034.(CHEN T, LUO X G, LI X N, et al. An architecture of stream based reconfigurable clustered block cipher processing array [J]. Journal of Electronics & Information Technology, 2014, 36(12): 3027-3034.)

[5] HUANG M, NARAYANA V, BAKHOUYA M, et al. Efficient mapping of task graphs onto reconfigurable hardware using architectural variants [J]. IEEE Transactions on Computers, 2012, 61(9): 1354-1360.

[6] JIAN Y C, WANG J F. Temporal partitioning data flow graphs for dynamically reconfigurable computing [J]. IEEE Transactions on Very Large Scale Integration Systems, 2007, 15(12): 1351-1361.

[7] OUNI B, AYADI R, MTIBAA A. Temporal partitioning of data flow graph for dynamically reconfigurable architecture [J]. Journal of Systems Architecture, 2011, 57(8): 790-798.

[8] OU C W, RANKA S. Parallel incremental graph partitioning [J]. IEEE Transactions on Parallel & Distributed Systems, 1997, 8(8): 884-896.

[9] CARDOSO J, P O M, DINIZ P C, et al. Compiling for reconfigurable computing: a survey [J]. ACM Computing Surveys, 2010, 42(4): 1301-1365.

[10] YIN C, YIN S, LIU L, et al. Temporal partitioning algorithm for a coarse-grained reconfigurable computing architecture [C]// Proceedings of the 2009 IEEE International Symposium on Integrated Circuits. Piscataway, NJ: IEEE, 2009: 659-662.

[11] PURNA K M G, BHATIA D. Temporal partitioning and scheduling data flow graphs for reconfigurable computers [J]. IEEE Transactions on Computers, 1999, 48(6): 579-590.

[12] 周博,邱卫东,谌勇辉,等.基于簇的层次敏感的可重构系统任务划分算法[J].计算机辅助设计与图形学学报,2006,18(5):667-673.(ZHOU B, QIU W D, CHEN Y H, et al. A level sensitive cluster based partitioning algorithms for reconfigurable systems [J]. Journal of Computer-Aided Design & Computer Graphics, 2006, 18(5): 667-673.)

[13] 陈乃金,江建慧.融合面积估算和多目标优化的硬件任务划分算法[J].通信学报,2013,34(2):40-55.(CHEN N J, JIANG J H. Hardware-task partitioning algorithm merged area estimation with multi-objective optimization [J]. Journal on Communications, 2013, 34(2): 40-55.)

[14] SHENG W, HE W, JIANG J, et al. Pareto optimal temporal partition methodology for reconfigurable architectures based on multi-objective genetic algorithm [C]// Proceedings of the 2012 IEEE 26th International Parallel and Distributed Processing Symposium Workshops & PhD Forum. Piscataway, NJ: IEEE, 2012: 425-430.

[15] ZHOU Y, SHENG W, LIU X, et al. Efficient temporal task partition for coarse-grain reconfigurable systems based on simulated annealing genetic algorithm [C]// Proceedings of the 2011 IEEE 9th International Conference on ASIC. Piscataway, NJ:IEEE, 2011: 941-944.

[16] KAO C C. Performance-oriented partitioning for task scheduling of parallel reconfigurable architectures [J]. IEEE Transactions on Parallel & Distributed Systems, 2015, 26(3): 858-867.

This work is partially supported by the National Science and Technology Major Project (2016ZX01012101), the National Natural Science Foundation of China (61572520, 61521003).

YUANKaijian, born in 1993, M. S. candidate. His research interests include chip system design, reconfigurable computing.

ZHANGXingming, born in 1963, M. S., professor. His research interests include broadband information network, high performance computing.

GAOYanzhao, born in 1984, Ph. D., assistant research fellow. His research interests include high performance computing.

Taskpartitioningalgorithmbasedonparallelismmaximizationwithmulti-objectiveoptimization

YUAN Kaijian*, ZHANG Xingming, GAO Yanzhao

(NationalDigitalSwitchingSystemEngineering&TechnologicalResearchCenter,ZhengzhouHenan450002,China)

Concerning the parallelism maximization of hardware task partitioning in reconfigurable system, a task partitioning algorithm based on parallelism maximization for multi-objective optimization was proposed. Firstly, the operating nodes to be partitioned were discovered according to the breadth first search under the constraints of hardware area resource and reasonable dependency relation. Then, considering the effect of execution delay on system completion time, the parallelism of intra-block operations was maximized. Finally, the new nodes were accepted under the principle of reducing the fragment area without increasing the number of connections between blocks. Otherwise, a block partitioning was ended. The experimental results show that the proposed algorithm achieves the maximum intra-block parallelism and reduces the number of blocks and connecting edges compared with the existing Level Based Partitioning (LBP) and Cluster Based Partitioning (CBP) algorithms.

reconfigurable system; task partitioning; parallelism maximization; multi-objective optimization; breadth first search

TP316

:A

2017- 01- 24;

:2017- 03- 08。

国家科技重大专项(2016ZX01012101)；国家自然科学基金资助项目(61572520, 61521003)。

袁开坚(1993—)，男，江苏淮安人，硕士研究生，主要研究方向：芯片系统设计、可重构计算； 张兴明(1963—)，男，河南新乡人，教授，硕士，主要研究方向：宽带信息网络、高性能计算； 高彦钊(1984—)，男，河北平山人，助理研究员，博士，主要研究方向：高性能计算。

1001- 9081(2017)07- 1916- 05

10.11772/j.issn.1001- 9081.2017.07.1916