基于协整分析的中国大陆农村人口死亡率预测

卢静会，张建，2，何华

（1.河北工业大学理学院，天津300401；2.中央财经大学保险学院，北京100081）

基于协整分析的中国大陆农村人口死亡率预测

卢静会1，张建1，2，何华1

（1.河北工业大学理学院，天津300401；2.中央财经大学保险学院，北京100081）

为了弥补中国大陆农村人口死亡率历史数据缺乏，通过协整分析发现中国大陆农村和台湾地区的人口死亡率具有长期均衡关系，应用基于向量误差修正模型的人口死亡率预测方法进行预测，结果表明该模型拟合效果较好.通过计算发现中国大陆农村60岁人口的平均余命逐渐延长，未来农村养老必将面临严峻的人口老龄化问题.

Lee-Carter模型；死亡率预测；长期均衡关系；向量误差修正模型；平均余命

0 引言

随着居民生活水平和医疗状况的持续改善，死亡率呈现出不断下降的趋势，人类寿命明显延长，老龄化问题日益突出.在中国农村地区，由于大批年轻人口的流出，人口老龄化的速度和水平都远超城镇地区，农村养老问题形势不容乐观.

精准预测死亡率是研究人口老龄化问题中的一项重要内容，对政府相关部门应对养老问题具有重要指导意义.目前，广受推崇的死亡率模型为Lee and Carter[1]提出的Lee-Carter模型，该模型为动态死亡率模型，各参数意义简单明了，在实际问题中应用型较强.不少学者通过协整分析对Lee-Carter模型进行了改进：Yang and Wang[2]通过协整分析发现美国和英国人口死亡率之间具有长期均衡关系，在此基础上建立了死亡率预测模型；张奕等[3]通过协整分析发现中国男性与日本男性人口死亡率具有长期均衡关系，在此基础上结合极值理论方法对中国死亡率进行了预测；柳向东等[4]通过协整分析发现中国大陆地区和台湾地区死亡率具有长期均衡关系，在此基础上建立了基于向量误差修正的死亡率预测模型.

本文应用基于向量误差修正模型（VECM）的人口死亡率预测方法，利用最新的数据对中国大陆农村人口死亡率进行预测，将其得到的预测值与基于传统ARIMA模型所得的进行比较，结果表明基于VECM模型的预测效果更好.在此基础上，计算可得中国大陆农村60岁人口的平均余命，通过比较发现此平均余命呈上升趋势，未来农村养老必将面临严峻的人口老龄化问题.

1 人口死亡率的预测模型

1.1 Lee-Carter模型

Lee-Carter模型的形式如下：

其中：T表示观察年的个数；mx，t表示年龄为x岁的人群在t年的中心死亡率；αx为依赖于年龄因子的参数，反映分年龄人口死亡率自然对数的平均水平；kt为依赖于时间因子的参数，反映人口死亡率的时间趋势；βx表示年龄因子对kt的敏感性；εx，t为残差项，满足E（εx，t）=0、Var（εx，t）=σ2.

基于上述假设，运用最小二乘法对各个参数进行估计，具体的估计表达式如下：

1.2 基于Kt的VECM模型的人口死亡率预测模型

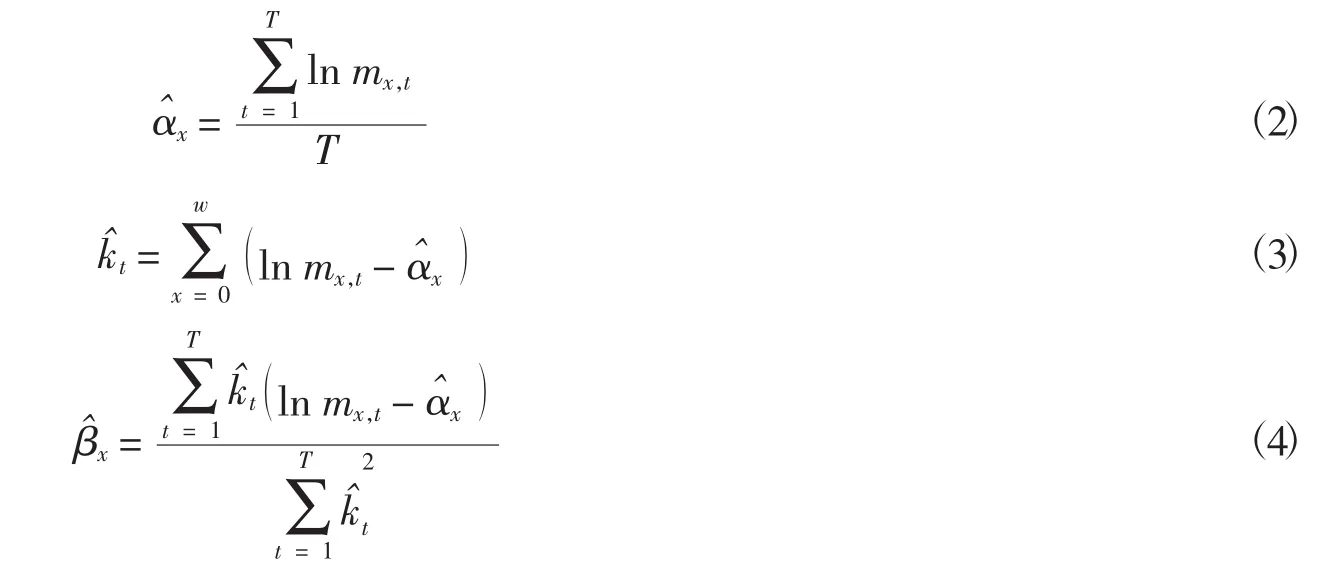
1.2.1 基于多国或多地区背景下人口死亡率模型的建立

用矩阵的形式表示出基于N个国家或地区的人口死亡率模型：

对于第j个国家或地区年龄为x的男性（女性）死亡率误差项的差分为：

1.2.2 建立Kt的VECM模型

协整分析要求每一个变量都是同阶非平稳的，所以假设Kt的每个子序列都为非平稳且p阶单整的，则Kt的p阶VECM模型如下所示：

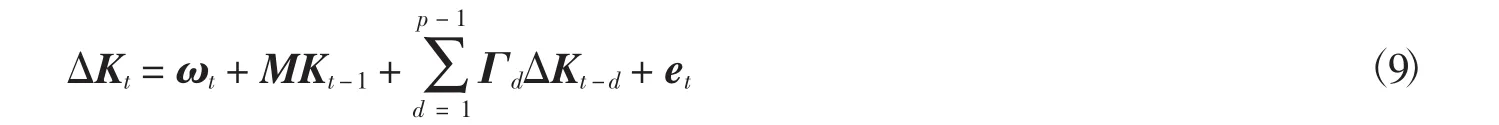
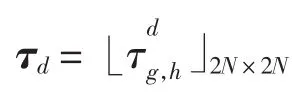
VECM模型的残差项et与Lee-Carter模型的残差差分项Δεx，t是相互独立的，对VECM模型进行迭代运算，可得Kt+n+1的公式：

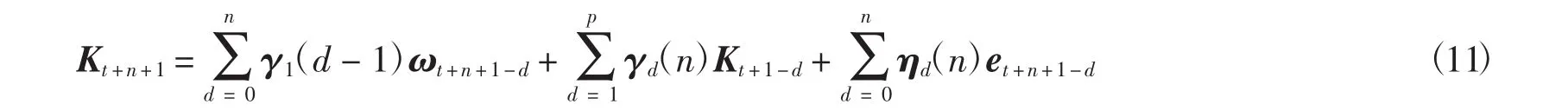
其中：γd（h）=γ1（h-1）τd+1（d＜h）γd+1（h-1），（d=1，…，p；h=1，…，n）；ηd（h）=ηd（d）1（d＜h）+γ1（h-1）1（d=h），（h=1，…，n）；γ1（-1）=I2N，η0（0）=I2N，γi（0）=τi，（i=1，…，p）.

1.2.3 基于多国或多地区背景下人口死亡率的预测模型

根据式（6）可得：

将式（11）代入式（12）中，化简可得：

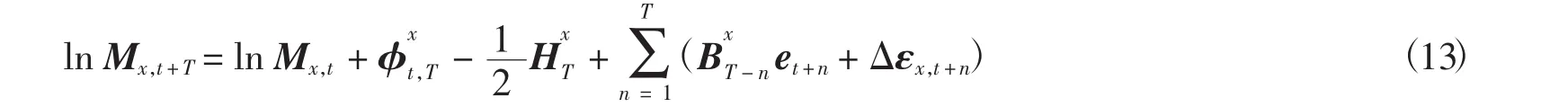
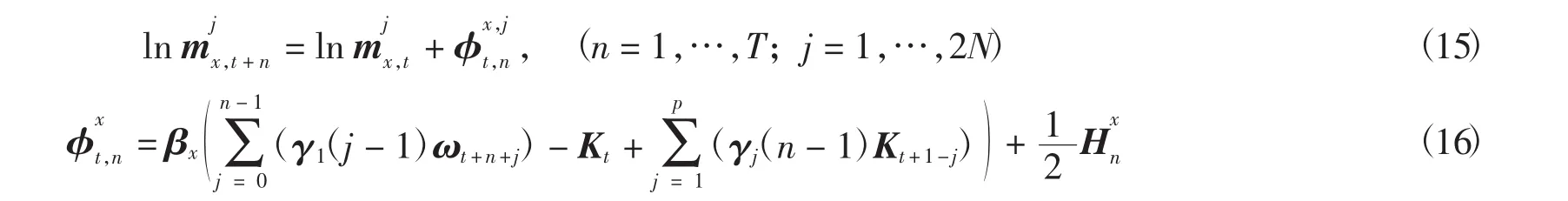
2 中国大陆农村人口死亡率的预测

2.1 原始数据的选择和处理

本文采用的原始数据为中国大陆农村1994～2014年分年龄、性别的人口死亡率，其中1995年的数据来自于《1995全国1%人口抽样调查资料》，2000年和2010年的数据分别来自于《第五次人口普查数据》和《第六次人口普查数据》，1994年、1996～1999年的数据来自于《中国人口统计年鉴》，2001～2009年、2011～2014来自于《中国人口与就业统计年鉴》.以5岁为一个年龄段对死亡率进行分组计算，分别为0～4岁，5～9岁，一直到85～89岁，90岁及以上，一共19组.对于台湾地区，采用的原始数据为1994～2014年以5岁为一个年龄段的人口死亡率，其来源于人类死亡率数据库（HMD），并对其进行处理使其与中国大陆农村人口死亡率数据分组相同.

将已处理的1994～2011年的数据代入式（2）～式（4）中，得到中国大陆农村和台湾地区关于参数αx、βx、kt的估计值.各个参数的估计值如图1所示.

从图1中可以看出，参数αx、βx、kt的估计值具有大致相同的变化趋势，这说明中国农村和台湾地区的人口死亡率可能存在长期均衡关系.

图1 参数αx、βx、kt的估计值Fig.1 Parameter estimates of αx、βx、kt

2.2 基于Kt的VECM模型的中国大陆农村人口死亡率的预测

然后，通过AIC和SC准则确定VECM模型的滞后阶数，这2个准则均要求数值越小模型的效果越好，如表2所示.

从表2可得，在滞后一阶时AIC和SC准则所对应的值都比滞后二阶时小，故此模型的最佳滞后阶数为一阶.

表1 单位根检验结果Tab.1 Unit root test results

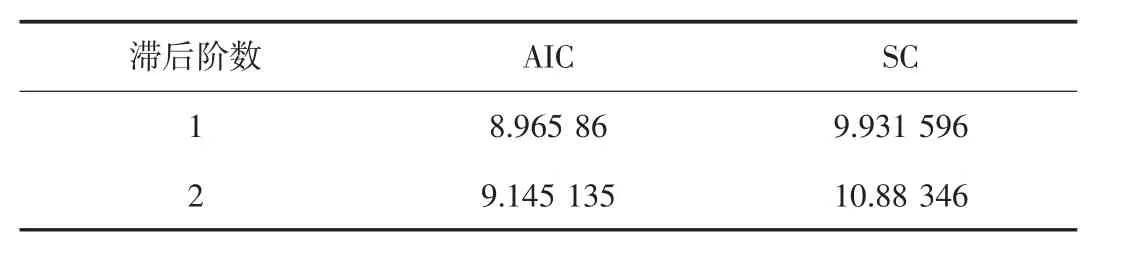
表2 VECM模型的滞后阶数的检验标准Tab.2 Selection criteria of the lag order for the VECM model

从表3可知，当原假设为无协整关系时，该假设所对应的p值为0.046 4，于是拒绝原假设，认为至少存在一个协整关系；当原假设为最多有一个协整关系，该假设所对应的p值为0.201 7，于是接受原假设，认为存在一个协整关系.

最后，根据中国大陆农村与台湾地区的时间因子序列得到下面的VECM（1）模型，即

表3 Johansen协整检验表Tab.3 Johansen test for co-integration results

2.3 预测误差分析

为了得到VECM模型对死亡率预测效果的影响，本节将利用传统的时间序列分析方法对2012-2014年的人口死亡率进行预测，并将2种方法所得的预测值与真实值进行比较.

以1994～2011年的中国大陆农村死亡率数据为基础，运用AIC和SC信息准则得到最适合中国大陆农村女性、男性kt的ARIMA模型都为ARIMA（0，1，1），通过Lee-carter模型预测出2012～2014年人口死亡率.以最小均方预测误差（MSPE）和平均绝对误差（MAE）作为评判预测效果的标准，两者分别为

其中ωi表示人口死亡率的真实值和预测值的差.

表4 男性死亡率预测误差Tab.4 error of prediction for male mortality

表5 女性死亡率预测误差Tab.5 error of prediction for female mortality

从表4和表5可得，除2013年中国大陆农村男性的基于ARIMA模型预测误差稍小以外，基于VECM模型所得的男性和女性死亡率误差均比基于ARIMA模型所得的小，这就说明基于VECM模型的预测方法效果更好.

2.4 平均余命的预测

采用1994～2014年的中国大陆农村人口死亡率数据，重新估计获得基于VECM的人口死亡率预测模型，并预测出2015～2023年分性别、年龄的人口死亡率.在此基础上，以目标时间各年龄组人口的死亡率水平代替分年龄人口在不同年龄的死亡率水平，按照段白鸽[9]所提出的方法预测出2014～2023年60岁人口的平均余命，如图2所示.

图2 中国大陆农村2014～2023年60岁人口的平均余命Fig.2 Life expectancy of population of 60 in the rural areas of China

从图2可看出在2014～2023年的这10年时间里，中国大陆农村60岁女性的平均余命从22.1岁增长到22.7岁，中国大陆农村60岁男性的平均余命从18.8岁增长到19.6岁，从而可得出以下结论：1）随着时间的延续，中国大陆农村60岁男性、女性的平均余命逐渐延长；1）在相同的日历年，中国大陆农村60岁的女性的平均余命明显高于男性.

3 结论

相较于基于ARIMA建立的死亡率预测模型，基于向量误差修正建立的人口死亡率预测模型不仅弥补了中国大陆农村死亡率历史数据缺乏，而且有效地提高了死亡率预测的精确性.由于居民生活水平和医疗状况的持续改善，本文中预测出的平均余命只是理论上的期望，但是中国大陆农村60岁人口的平均余命逐渐延长这一趋势毋庸置疑，这表明我国未来农村养老必将面临严峻的人口高龄化问题.

[1]Lee R D，Carter L R.Modeling and Forecasting US Mortality[J].Journal of the American Statistical Association，1992，87（419）：659-671.

[2]Yang S S，Wang C W.Pricing and Securitization of Multi-country Longevity Risk with Mortality Dependence[J].Insurance：Mathematics and Economics，2013，52（2）：157-169.

[3]张奕，王婷婷.基于协整理论的中国人口死亡率预测[J].高校应用数学学报，2015，30（1）：1-9.

[4]柳向东，范洋洋.基于均衡关系的中国人口死亡率预测模型[J].统计与信息论坛，2016，31（10）：3-9.

[5]Lin Y，Cox S H.Securitization of Mortality Risks in Life Annuities[J].The Journal of Risk and Insurance，2005，72（2）：227-252.

[6]Denuit M，Devolder P，Goderniaux A C.Securitization of Longevity Risk：Pricing Survivor Bonds with Wang Transform in the Lee-Carter Framework [J].The Journal of Risk and Insurance，2007，74（1）：87-113.

[7]尚勤，秦学志，周颖颖.死亡强度服从Ornstein-Uhlenbeck跳过程的长寿债券定价模型[J].系统管理学报，2008，17（3）：297-302.

[8]胡仕强.基于Lee-Carter模型和王变换方法的长寿债券定价研究[J].商业研究，2015，462：82-88.

[9]段白鸽.我国全年龄段人口平均预期寿命的动态演变[J].人口与经济，2015，1：49-63.

[10]刘娟，杨明旭.Lee-Carter估计模式推算中国农村老年人口死亡率的研究[J].南方人口，2011，4（26）：10-15.

[责任编辑 杨屹]

Mortality prediction of Chinese rural population based on the co-integration analysis

LU Jinghui1，ZHANG Jian1，2，HE Hua1
（1.Hebei University of Technology,School of Sciences,Tianjin 300401;2.Central University of Finance and Economics, Insurance Institute,Beijing 100081）

To make up for the lack of historical data of mortality in the rural areas of China,the long-run equilibrium of mortality rates between rural areas of China Mainland and Taiwan is found by the co-integration analysis,and a vector error correction model is applied to project the mortality.The result shows that the model fits well.Life expectancy of population of 60-year-old will increase obviously,which leads to the heavy risks of population aging faced in rural old-age care.

Lee-Carter model;mortality prediction;long-run equilibrium;vector error correction model;life expectancy

C921

A

1007-2373（2017）04-0111-07

10.14081/j.cnki.hgdxb.2017.04.019

2017-02-21

国家自然科学基金（11471218，11701139）；教育部人文社会科学重点研究基地重大项目（14JJD790001）

卢静会（1992-），女，硕士研究生，1742147426@qq.com.通讯作者：张建（1982-），男，实验师，zhangjian@hebut.edu.cn.