基于神经网络的矩形钢管混凝土破坏模态研究

陈志华，李红星，王小盾

（天津大学建筑工程学院，天津300072）

基于神经网络的矩形钢管混凝土破坏模态研究

陈志华，李红星，王小盾

（天津大学建筑工程学院，天津300072）

为了研究矩形钢管混凝土柱轴压破坏模态，总结了大量文献的试验数据，并采用Abaqus进行有限元模拟，有限元模拟结果作为研究破坏模态的补充数据.分析结果表明矩形钢管混凝土柱轴压的破坏模态主要分为受压和受弯2种，长细比是影响破坏模态类型的最主要的因素.通过神经网络的预测方法研究受压及受弯2种破坏模态的长细比临界值，同时对矩形钢管混凝土柱的轴压受压受弯破坏模态长细比临界值进行了参数化分析.结果表明：在本文研究参数范围内，受压与受弯2种破坏模态的长细比临界值为32左右，长宽比（长/宽）越小，含钢率越大，约束效应系数越大，临界值越大；混凝土强度越大，临界值越大；钢管厚度越大，约束效应系数越大，临界值越小；钢材强度越大，约束效应系数越大，临界值越小.

矩形钢管混凝土柱；神经网络；轴压破坏模态；长细比；参数化

钢管混凝土按截面形式不同，可分为圆钢管混凝土、方钢管混凝土和矩形钢管混凝土等，矩形钢管混凝土是指截面边长（长边D和短边B）不相等的情况.方、矩形钢管对其核心混凝土的约束效果不如圆钢管显著，但仍有良好的效果，尤其可以有效地提高构件的延性，另外，与梁连接节点的构造处理也较简便，因此受到土木工程师们的青睐.目前，国内外对矩形钢管混凝土的研究都集中于其力学性能的研究[1-4]，没有针对其破坏模态进行研究.本文拟研究矩形钢管混凝土的破坏模态类型及其影响因素，以期得出可供工程参考的结论，为研究钢管混凝土的柱子曲线提供参考资料.

1 研究背景

1.1 矩形钢管混凝土破坏模态

由本文通过汇总大量文献[5-9]的试验数据及试验现象，得出以下几种矩形钢管混凝土柱主要的破坏模态：1）受压破坏，钢管先局部屈曲，随后达到极限承载力，混凝土压碎，破坏现象表现为柱子局部向外鼓曲；2）剪切破坏，混凝土过早剪切，试件未达到极限承载力；3）受弯破坏，试件达到最大承载力，由于偏心率、初始缺陷、长细比等因素影响，破坏现象表现为试件呈现整体屈曲，跨中侧向挠度最大，试件中部混凝土被压碎；4）失稳破坏，由于试件长细比过大等原因导致试件出现整体失稳，钢管混凝土柱的跨中突然发生较大的侧向挠度，不能继续承载，试件未达到极限承载力.

由于文献试验数据的局限性，本文主要考虑矩形钢管混凝土柱轴压的受压破坏及受弯破坏.试验数据总结如表1所示.

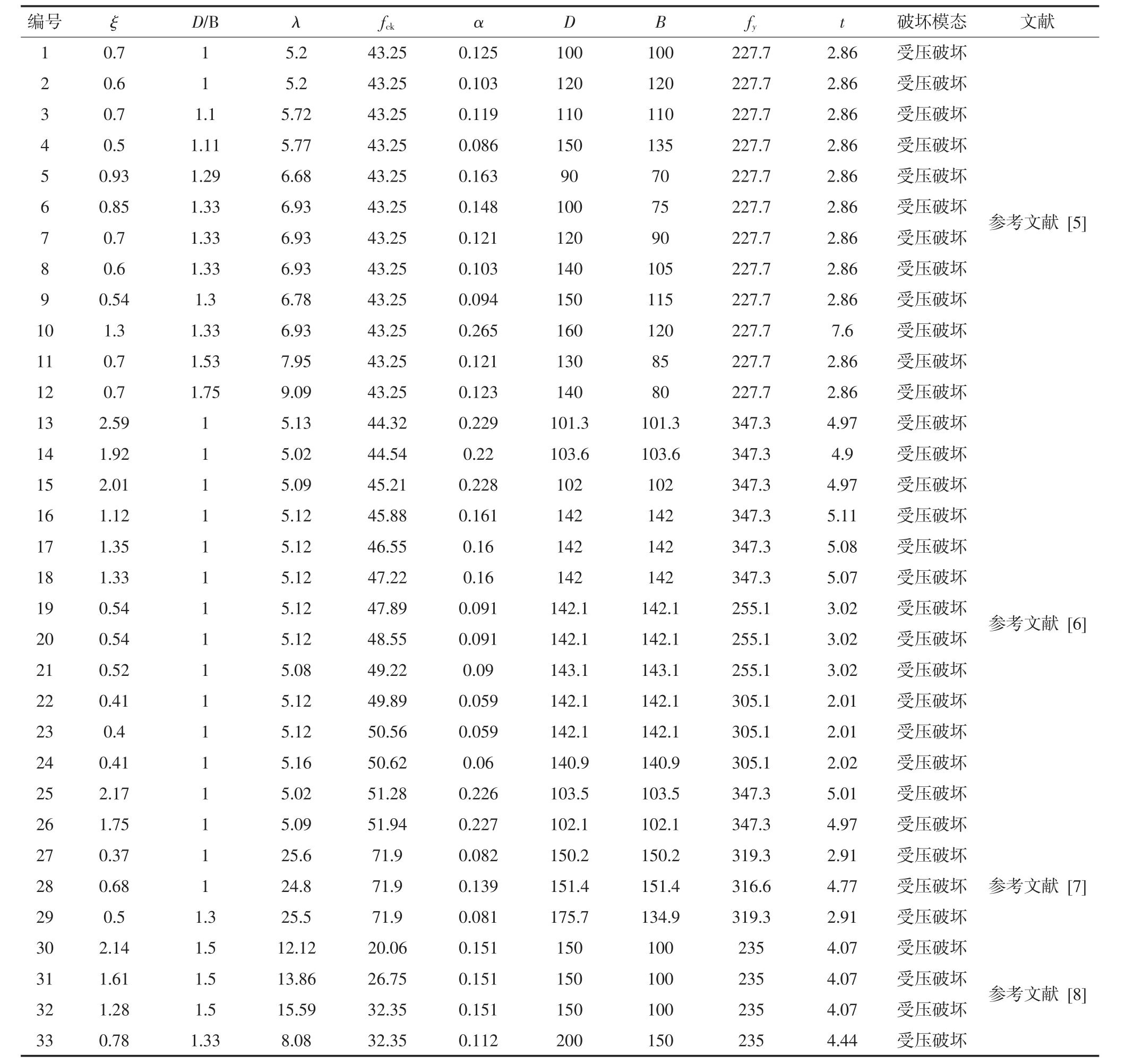
表1 文献数据汇总Tab.1 The database collected from the literature

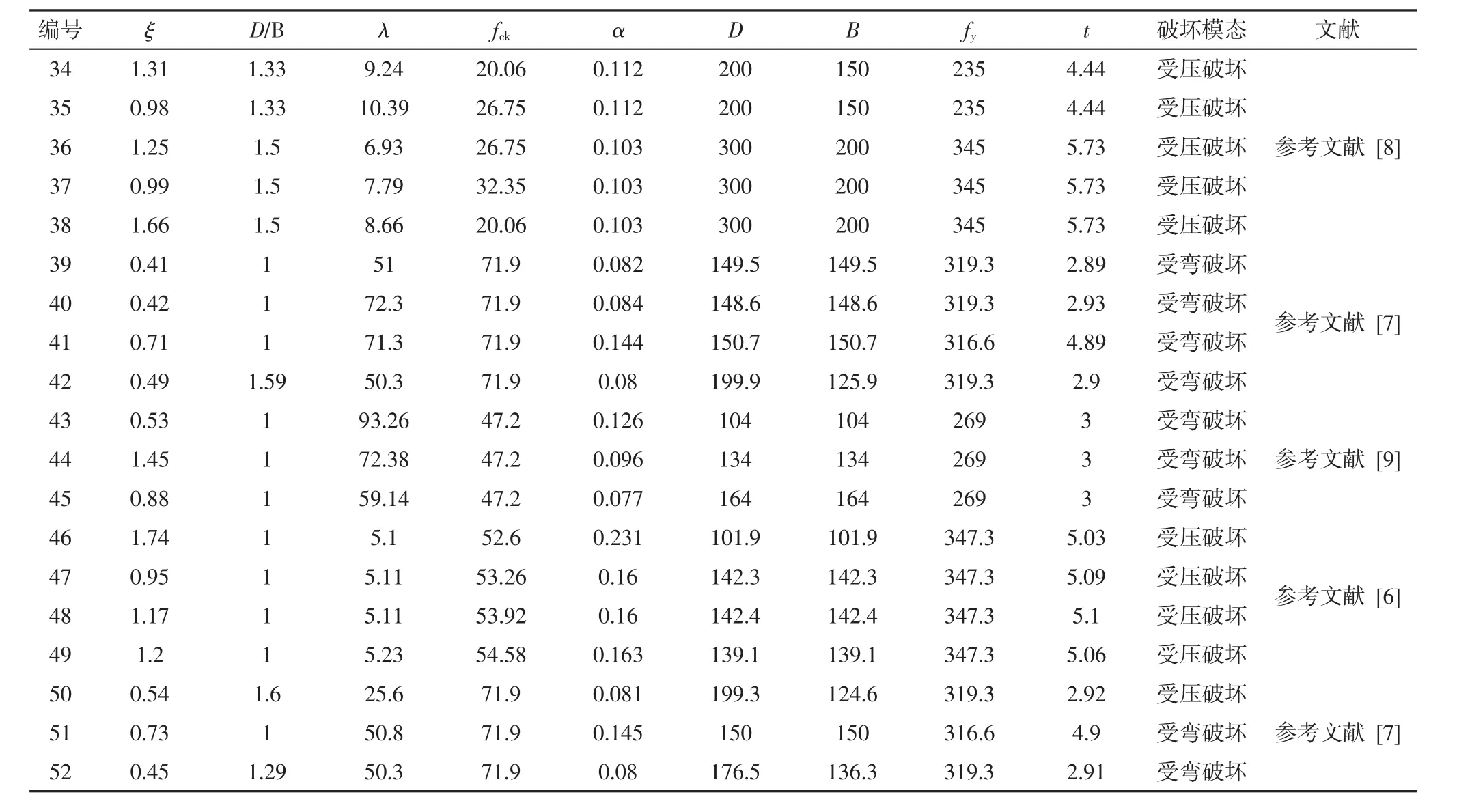
续表1文献数据汇总Tab.1 The database collected from the literature

1.2 神经网络研究方法概述

人工神经网络（Artificial Neural Networks，ANNs）也简称为神经网络（NNs），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型.这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的.神经网络在处理非线性复杂问题上具有突出优点，而其自学习功能对于预测有重要意义[10].BP网络是应用最多的神经网络，可以实现从输入到输出的任意非线性映射，其基本原理见图1.因此，许多学者在神经网络用于钢管混凝土构件的工作中进行了许多有意义的尝试.朱美春等[11]将BP网络用于方钢管混凝土计算，表明其模型具有良好的学习精度和较好的泛化能力.郝艳娥等[12]用BP网络预测矩形钢管混凝土柱的承载力，结果表明，与传统方法相比，计算简单且结果准确.Wang Haijun等[13]对受偏压的方钢管混凝土进行神经网络模拟，预测结果准确，并且随着数据量的增加，拟合效果更好.

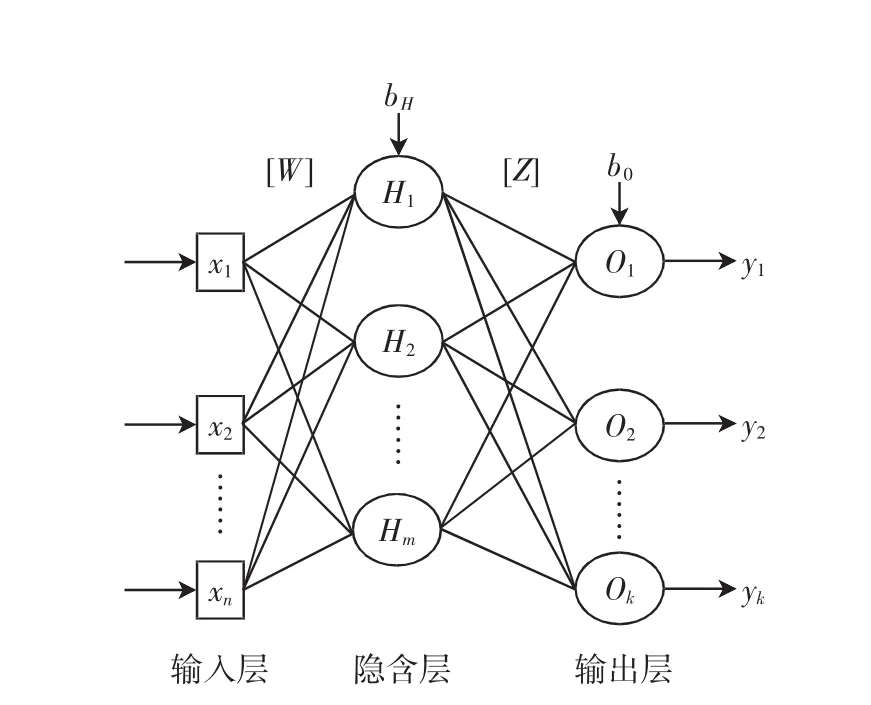
图1 神经网络结构图Fig.1 The structures of the neural networks

2 有限元模拟

2.1 本构关系

用于有限元模拟的矩形钢管混凝土柱的材料力学性能参数选取韩林海[4]的试件rc1-1试验数据，改变长细比进行模拟.ABAQUS软件中的塑性（*PLASTIC）模型可以模拟多线性或双线性应力-应变关系曲线[14]，本文钢材采用理想弹塑性模型，钢材屈服强度fy和抗拉极限强度fu和弹性模量取试验实测值，分别为227.7 MPa、294.4 MPa、182 000 MPa，混凝土采用混凝土损伤塑性模型[15]，单轴受压应力-应变关系采用文献[16]中修正的钢管混凝土中核心混凝土的本构关系，如下式：

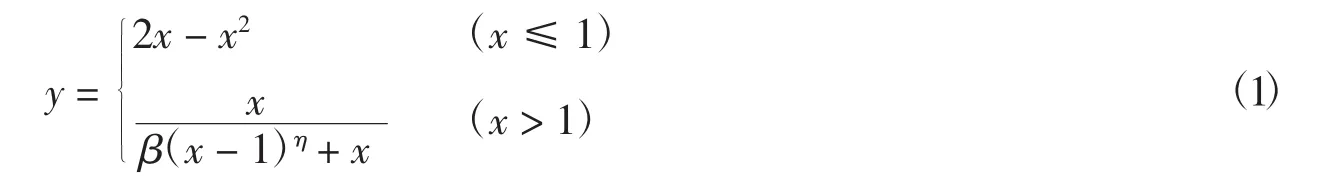
混凝土泊松比νc取0.2，设置混凝土受拉开裂时的应变为0[17].计算中的混凝土的弹性模量Ec按规范ACI取值，为33 234 MPa；轴心抗压强度fck按C60混凝土的换算公式fck=0.65 fcu进行换算，其中fcu取试验值为59.3 MPa.

2.2 有限元模拟结果

本文考虑初始缺陷，先对韩林海[5]的rc1-1试件进行有限元模拟，模拟结果和实际试验结果吻合较好（见表2），表明该有限元模型可以对矩形钢管混凝土的破坏模态进行正确的模拟.为了补充文献数据，有限元模型的长细比取值为20、25、30、35、37.24、38.11、38.97、40、45、50.有限元模型的基本数据如表2所示.有限元分析结果表明，长细比为20、25、30的柱子最终为受压破坏，破坏过程中试件中部呈现局部鼓曲；长细比为35、37.24、38.11、38.97、40、45、50的柱子最终为受弯破坏，试件呈现整体弯曲，试件中部侧向挠度最大.试件最终破坏模态和荷载位移曲线分为如图2、图3所示.

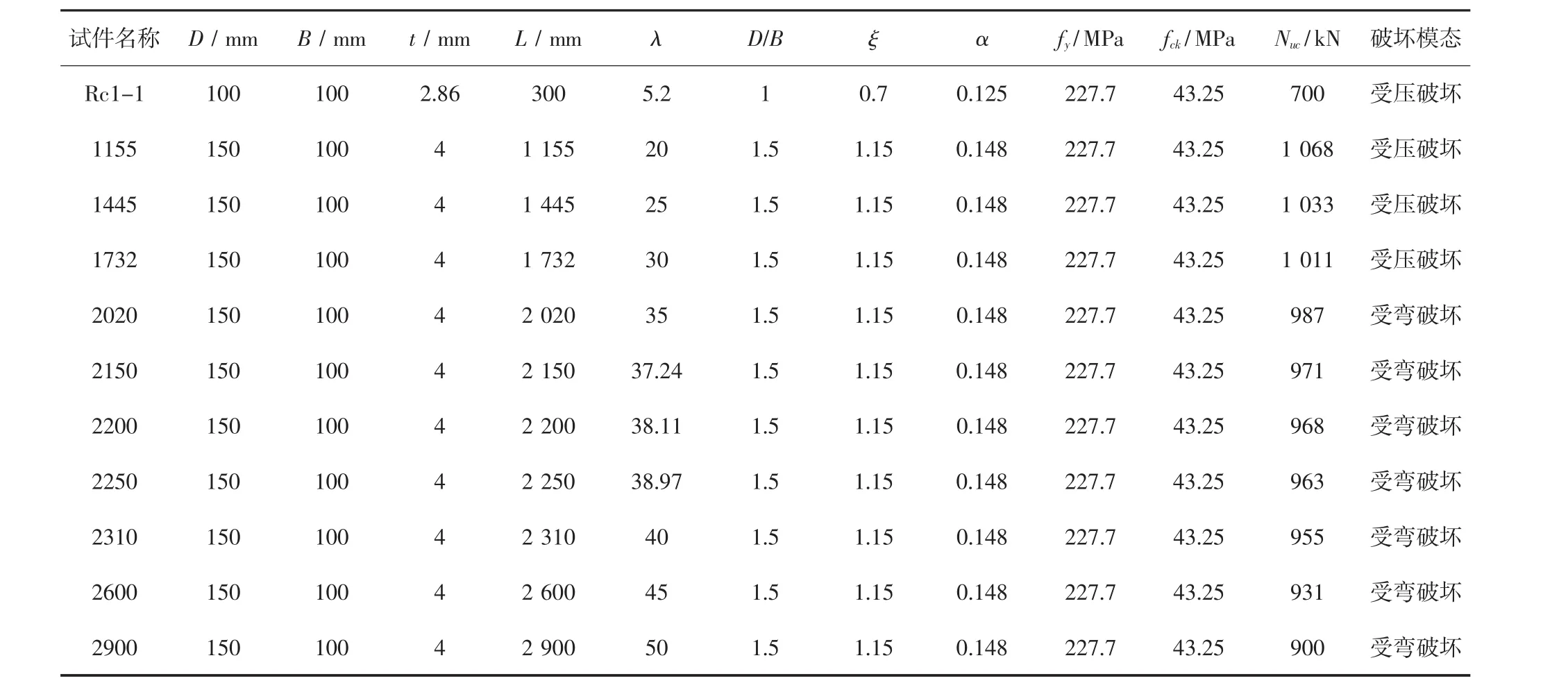
表2 有限元模型基本数据Tab.2 The details of the finite element models

图2 矩形钢管混凝土柱2种典型破坏模态Fig.2 Two typical failure modes of the rectangular CFT columns

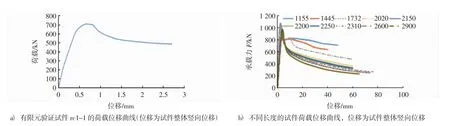
图3 有限元模型模拟结果-矩形钢管混凝土柱荷载位移曲线Fig.3 The load-displacement curves of the finite element models and the test results

3 神经网络预测破坏模态

3.1 神经网络模型

使用MATLAB（R2014a）神经网络工具箱建立神经网络模型，采用基于BP算法的多层前馈网络来进行模拟.

本文采用表1文献中的试验数据以及表2有限元模拟的数据，共62组数据，其中的54组进行网络模型训练，8组数据进行预测.长细比范围为5.02～93.26；试件厚度范围为2.86～7.6 mm；混凝土棱柱体抗压强度标准值范围为20.06～71.9 MPa；钢管屈服强度范围为194～495 MPa.网络隐含层和输出层变换函数均选择线性（purelin），采用收敛速度最快的trainlm训练算法，取学习效率lr=0.05，最大训练步数epochs=2 000，控制误差goal=0.001，附加动量因子0.95.训练之前对数据做了归一化处理，这样便于网络快速收敛.

模型均采用一个20节点的隐含层，如图4所示.

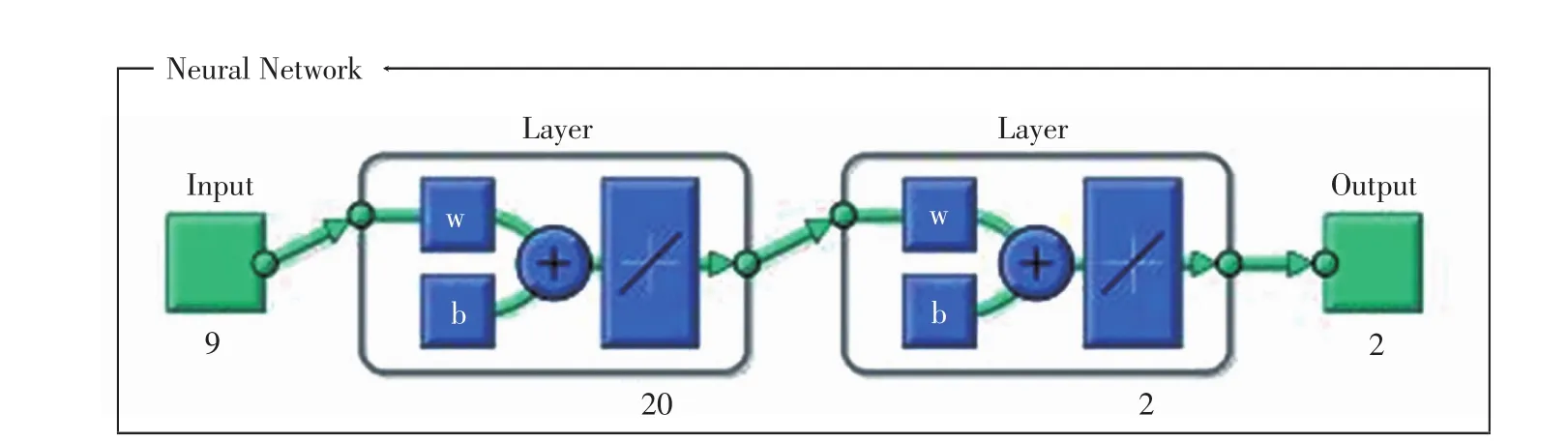
图4 神经网路ANN-1结构图Fig.4 The structures of the neural network ANN-1

3.2 神经网络模型的预测结果

8组预测数据实际输出为Ttest，参考输出为ttest，参考曹庆林应用神经网络进行围岩类别判断的研究[18]，本文中ttest=[1，0]表示矩形钢管混凝土柱为受压破坏，ttest=[0，1]表示矩形钢管混凝土柱为受弯破坏.实际输出向量[a，b]，若a＞b，则可以判断该矩形钢管混凝土柱为受压破坏；若a＜b，则可以判断该矩形钢管混凝土柱为受弯破坏.预测结果与参考破坏类型吻合良好，如表3所示，说明本文训练的神经网络模型可以应用于矩形钢管混凝土柱轴压破坏模态的预测.随后，利用该神经网络模型，只改变长细比的值，其他输入变量的值保持不变，ξ=0.71，D=150 mm，B=100 mm，fck=43.25 MPa，ɑ=0.148，fy= 227.7 MPa，t=4 mm.预测出矩形钢管混凝土柱轴压的受压破坏与受弯破坏的长细比临界值为32，其预测输出Ttest为[0.500 1，0.499 9].

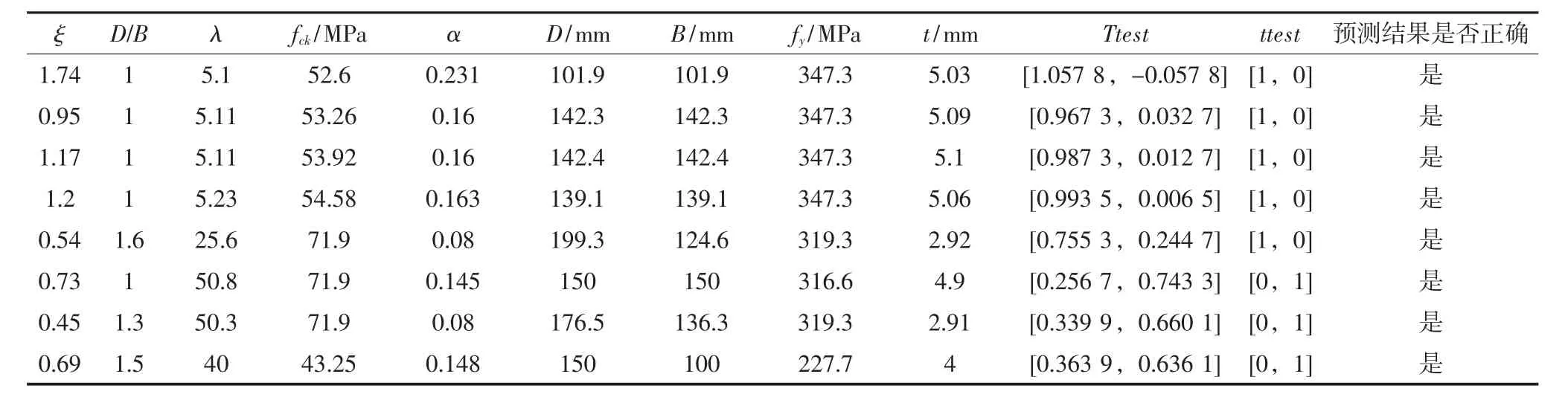
表3 神经网络预测结果Tab.3 The results of the neural networks

控制单一变量，进行参数化分析，研究约束效应系数、长宽比、混凝土强度、含钢率、钢管厚度、钢材强度对长细比限值的影响.研究结果表明，矩形钢管混凝土柱轴压的受压破坏与受弯破坏的长细比临界值大小与约束效应系数、长宽比、混凝土强度、含钢率、钢管厚度、钢材强度有关.长宽比（长/宽）越小，含钢率越大，约束效应系数越大，临界值越大；混凝土强度越大，临界值越大；钢管厚度越大，约束效应系数越大，临界值越小；钢材强度越大，约束效应系数越大，临界值越小，结果如图5所示.

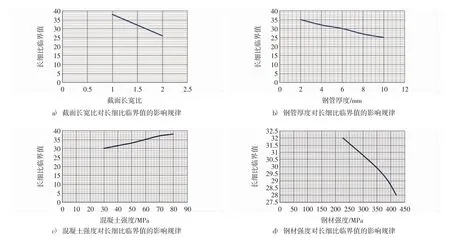
图5 长细比临界值变化规律Fig.5 The variations of the slenderness ratio threshold with different parameters

4 结论

基于上述研究内容，在本文研究参数范围内，可初步得出如下结论：

1）矩形钢管混凝土柱轴压破坏模态主要有受压破坏及受弯破坏，长细比是影响破坏类型的最主要的因素.

2）神经网络可以用于预测矩形钢管混凝土柱轴压破坏模态，在本文给定情况下，受压破坏及受弯破坏的长细比临界值为32.

3）矩形钢管混凝土柱轴压的受压破坏与受弯破坏的长细比临界值大小与约束效应系数、长宽比、混凝土强度、含钢率、钢管厚度、钢材强度有关.长宽比（长／宽）越小，含钢率越大，约效应系数越大，临界值越大；混凝土强度越大，临界值越大；钢管厚度越大，约束效应系数越大，临界值越小；钢材强度越大，约束效应系数越大，临界值越小.

[1]谭克峰，蒲心诚.钢管超高强混凝土长柱及偏压柱的性能与极限承载力的研究[J].建筑结构学报，2002，21（2）：12-19.

[2]Eurocode 4，EN 1994-1-1 Design of composite steel and concrete structures，Part 1.1.General rules and rules for buildings[S].British Standards Institution，2004.

[3]Lam D，Williams C A.Experimental study on concrete filled square hollow sections[J].Steel and Composite Structures，2004，4：95-112.

[4]尧国皇.钢管混凝土构件在复杂受力状态下的工作机理研究[D].福州：福州大学，2006.

[5]韩林海，杨有福.矩形钢管混凝土轴心受压构件强度承载力的试验研究[J].土木工程学报，2001，34（4）：22-31.

[6]张素梅，郭兰慧，叶再利，等.方钢管高强混凝土轴压短柱的试验研究[J].哈尔滨工程大学学报，2004，34（12）：1610-1614.

[7]郭兰慧，张素梅.截面长宽比对矩形钢管高强混凝土轴压构件的影响[J].哈尔滨工业大学学报，2003，35（增刊）：155-159.

[8]曲秀姝.矩形钢管混凝土柱共同工作组合力学性能研究[D].天津：天津大学，2011：95-103.

[9]Mursi Mohanad，Uy Brian.Strength of concrete filled steel box columns incorporating interaction buckling[J].Journal of structural engineering，2003，5：626-639.

[10]张德丰.MATLAB神经网络应用设计[M].北京：机械工业出版社，2012：37-50.

[11]朱美春，王清湘，冯秀峰.方钢管混凝土短柱轴心受压承载力的神经网络模拟[J].计算力学学报，2006（3）：252-255.

[12]郝艳娥，翟振东.矩形钢管混凝土短柱轴压承载力神经网络评估[J].长安大学学报（建筑与环境科学版），2004，21（3）：24-28.

[13]Wang Haijun，Zhu Huabei，Wei Hua.Bearing capacity of concrete filled square steel tubular columns based on neural network[J].Advanced Materials Research，2012，502：193-197.

[14]韩林海.钢管混凝土结构：理论与实践[M].第2版.北京：科学出版，2007.

[15]韩庆华，王一泓，徐杰，等.弹性混凝土-钢组合梁非线性数值分析[J].天津大学学报：自然科学与工程技术版，2014，47（增刊）：91-95.

[16]刘威.钢管混凝土局部受压时的工作机理研究[D].福州：福州大学，2005：62-66.

[17]陈志华，杜颜胜，周婷.配螺旋箍筋方钢管混凝土柱力学性能研究[J].建筑结构，2015，45（20）：28-33.

[18]曹庆林.用神经网络方法预测围岩类别[J].冶金矿山设计与建设，1994（5）:12-14.

[责任编辑 杨屹]

Study on the failure mode of concrete-filled rectangular steel tubular columns based on artificial neural network

CHEN Zhihua,LI Hongxing,WANG Xiaodun
（School of Civil Engineering,Tianjin University,Tianjin 300072,China）

In order to study on the failure mode of concrete-filled rectangular steel tubular columns(CFT)under axial compression,the article summarizes a lot of test data and uses Abaqus to simulate the failure mode,the results of simulation are used as supplemental data.The results show that the major failure mode of CFRT on axial compression can be divided into two kinds called compression and flexural,and slenderness ratio is the most important factor affecting the type of failure mode.We also studied on the threshold of slenderness ratio based on forecasting method neural network.At the same time,parameter analysis of slenderness ratio threshold was conducted with the neural network.The results show that the slenderness ratio of two types of failure mode is about 32.The smaller Aspect ratio(length/width)is,the greater steel ratio is,the greater confining factor is,the greater slenderness ratio is;the greater strength of concrete is,the greater slenderness ratio is;the greater steel thickness is,the greater confining factor is,the smaller slenderness ratio is;the greater strength of steel is,the greater confining factor is,the smaller slenderness ratio is.

concrete-filled rectangular steel tubular columns;artificial neural networks;failure mode;slenderness ratio;parameter analysis

TU398.9

A

1007-2373（2017）04-0104-07

10.14081/j.cnki.hgdxb.2017.04.018

2017-02-21

国家自然科学基金（61272264）

陈志华（1966-），男，教授，zhchen@tju.edu.cn.