超级均匀化方法用于球床氟盐冷却高温堆扩散计算

2017-09-19朱贵凤余笑寒

核技术 2017年9期

关键词：控制棒堆芯通量

戴明朱贵凤戴叶邹杨余笑寒

1（中国科学院上海应用物理研究所嘉定园区上海 201800）2（中国科学院核辐射与核能技术重点实验室上海 201800）3（中国科学院大学北京 100049）

超级均匀化方法用于球床氟盐冷却高温堆扩散计算

戴明1,3朱贵凤1,2戴叶1,2邹杨1,2余笑寒1,2

1（中国科学院上海应用物理研究所嘉定园区上海 201800）2（中国科学院核辐射与核能技术重点实验室上海 201800）3（中国科学院大学北京 100049）

球床氟盐冷却高温堆的控制棒位于侧反应射层内，存在无裂变中子源且受堆芯泄漏谱强烈影响的强吸收体区域扩散计算难题。超级均匀化方法(Super Homogenization, SPH)被用于对氟盐球冷却床堆侧反射层中控制棒区域的强吸收体进行等效均匀化处理，同时堆芯除控制棒区域外采用谱修正方法(Spectra Modification, SM)，将输运计算的结果作为基准进行验算。结果表明，SM-SPH模型能有效地计算球床氟盐冷却高温堆反射层控制棒价值及通量分布，并且较常规的SPH方法能更好地处理棒间干涉效应。

球床氟盐冷却高温堆，控制棒，超级均匀化方法，强吸收体

球床氟盐冷却高温堆(Pebble-Bed Fluoride-saltcooled High-temperature Reactors, PB-FHR)[1-4]的控制棒位于侧反射层中，强吸收体吸收截面远大于周围石墨介质，使得吸收体边界出现通量畸变，扩散近似失效。同时受堆芯泄漏谱影响，使得球床氟盐冷却高温堆的全堆扩散计算需要特别处理反射层中的强吸收体。高温气冷堆中同样存在反射层中控件棒计算问题，为了解决这个问题，大致有三种方法：1) 使用离散纵坐标方法（又称为SN方法）直接精细建模，进行传统的体积通量权重(Volume-Flux weighted Method, VFM)[5]；2) 采用等效截面方法[6]；3) 应用不连续因子局部均匀化强吸收体区域[7]。体积通量权重方法及等效截面方法并不能很好地保证强吸收体区域的反应率守恒及通量分布一致，而不连续因子方法需要使用支持不连续因子的扩散程序，并且需要扩散程序支持径向非零起点的扇形几何模型。本文利用同样在压水堆中成功使用的另一种等效均匀化方法，即超级均匀化方法(Super Homogenization, SPH)[8]，结合谱修正方法(Spectra Modification, SM)[9-10]来处理PB-FHR中扩散计算中的强吸收体。

1 超级均匀化的需求

如图1所示，反应堆模型的侧反射层中均匀布置有16根控制棒，控制棒插入形成强吸收体区域，控制棒拔出后为有一定中子吸收能力的熔盐区域。各种控制棒组合状态都可以由强吸收体区域和熔盐区域排列组合构成。球床堆全堆计算为了考虑谱区间相互泄漏的影响，通常采用谱修正方法，即使用全堆扩散计算的泄漏率来修正截面，显然谱修正方法不适用于强吸收体区。为此把强吸收体区域划分为超级均匀化区域，并使用SPH因子修正相应均匀化截面。为了计算SPH区域的SPH因子，选取包括强吸收体区域或熔盐区域的1/32扇形区域作为组件模型，并对由图1(b)所示的SPH区域进行等效均匀化处理，计算时组件模型上下边界为反射边界条件。全堆扩散计算时对于SPH区域采用SPH因子修正的少群常数，其他区域采用谱修正方法处理。

图1 PB-FHR带控制棒堆芯模型及组件模型(a) 非均匀反应堆模型，(b) 两类1/32扇形堆芯组件模型Fig.1 Reactor model of PB-FHR with control rods and its assemblies. (a) Heterogeneous reactor model, (b) Two kinds of 1/32 reactor core assemblies

2 SM-SPH方法原理

SM-SPH方法基本原理即将谱修正方法与SPH方法两者耦合。

谱修正方法即由堆芯扩散计算得到的谱区泄漏率计算谱区曲率，把该曲率反馈到谱区能谱计算，从而修正谱区截面。修正的谱区截面又用于堆芯扩散计算，所以谱修正过程是能谱计算与堆芯扩散计算之间迭代计算过程。

多群扩散方程可写为：

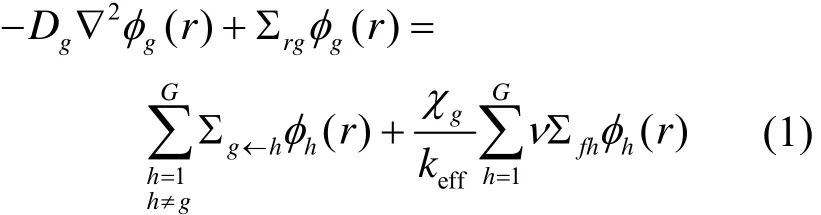
把扩散方程在指定区域体积内空间积分，有：

把堆芯划分不同谱区，对谱区体积进行空间积分（K、H为少群，n为第n次迭代），可得到少群曲率

谱区多群能谱计算方程为：

对式(7)进行并群：

要使能谱计算的式(8)与全堆扩散计算得到的谱区中子平衡方程式(6)等价，最直接的方式是令

超级均匀化的思想是通过引入SPH因子实现均匀化/并群前后反应率守恒。对于传统的体积通量权重均匀化，有：

式中：∑为均匀化截面；Σ为多群宏观截面。

通常这种体积通量权重均匀化得到截面并不能完全保证反应率守恒，为此，引入SPH修正因子μ，并定义等效截面：

为了保证反应率守恒，均匀化的积分通量与均匀化前存在如下关系：

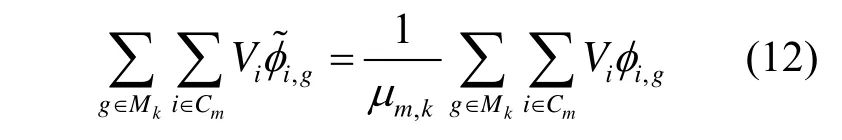
这样，可以通过迭代计算求出SPH因子。值得注意的是，中子通量求解对象为特征值方程，在求解SPH因子时，积分通量需要进行归一化处理。常用的归一化方法为使得非均匀和均匀计算的平均通量相等，而本文SM-SPH模型只对控制棒的强吸收体附近区域进行SPH修正，归一化方法选择为功率归一化，即输运参考解与扩散解都归一到指定功率。

SPH方法的应用需要知道确切的边界条件，为此谱修正方法能首先给它提供一个近似的边界条件。谱修正需要堆芯计算的净中子流信息修正截面，SPH修正能确保强收体附近区域反应率守恒，特别是泄漏率，为谱修正区域提供相对正确的净中子流信息。SPH区域与谱修正区域相互影响，可以通过迭代逼近参考输运解。

3 SM-SPH方法物理实现过程

SM-SPH方法的组件计算即只对部分区域划分为SPH区（如控制棒区和附近反射层），采用谱修正方法处理其他区域，通过迭代得到SPH区的SPH因子。SPH因子计算流程如图2所示。

1) 燃料球栅元计算得到球床燃料区考虑了双重非均匀性的有效均匀化截面，该截面用于如图1所示的组件SN输运计算，组件SN输运计算作为输运参考解，提供SPH区域的通量及体积通量权重均化截面，用于SPH因子计算与截面修正。

2) 假设SPH因子，并采用式(11)修正相应截面。

3) 对除SPH区域进行谱修正计算，即在能谱计算与扩散计算进行迭代计算，使得谱区能谱计算能考虑谱区间泄漏影响。

4) 由扩散解与输运参考解采用式(12)计算SPH因子，并判断SPH因子是否收敛，如果不收敛则返回到2)过程。

上述计算过程的双迭代部分只进行组件扩散计算，所以整个SPH因子计算所需的时间可接受。

图2 SM-SPH方法的SPH因子计算流程Fig.2 Flow chart for the SPH factors calculation.

4 组件SN输运参考解验证

本文使用二维SN程序TWOTRAN对TMSR-SF1 (Thorium Molten Salt Reactor-Solid Fuel 1)的控制棒进行精细建模计算，并与MCNP (Monte Carlo N Particle Transport Code)程序进行对比验证。TMSR-SF1的控制棒模型为同心圆柱形，最内部为空腔，内外套管为哈氏合金，中间为含B强吸收体，控制棒通道套管为C/C复合材料。TMSR-SF1相关参数如表1所示。

TWOTRAN对于控制棒区域构建如图3所示精细网格模型，进行107群P1S8的SN方法求解。其燃料区截面来源于SRAC栅元计算。为了验证这种建模方式计算的准确性，采用MCNP进行了验证，包括控制棒价值及通量分布。MCNP计算时采用以ENDF/B-VII库为基础加工到相应温度下的连续能量截面库，有效中子代数为200，每代粒子数为10万。均匀化宏观截面的计算采用文献[11]公式。快热分界能设为1.86 eV，使用F4卡和FM卡统计相关反应率来计算四因子。使用F1卡统计界面进出中子流，得到泄漏率，然后按定义求得不泄漏概率。

图3 TWOTRAN计算时控制区域精细网格建模Fig.3 Fine meshes of control rod region in TWOTRAN.

表2给出了组件计算时燃料区截面及四因子对比。由表2可知，所有结果两者都能符合。TWOTRAN计算的组件控制棒价值为0.17817，与MCNP结果(0.18012)相比偏低1.06%，这部分偏差的引入与燃料区的不泄漏概率PNL有关。控制棒插入时，会增加堆芯泄漏率，不泄漏概率由0.82变为0.72。SRAC计算的燃料吸收截面偏大，在控制棒插入时PNL增加的幅度会增大，有棒下的PNL偏大0.48%，明显高于无棒时0.14%，这是造成TWOTRAN计算价值偏大的主要原因。

表1 TMSR-SF1堆芯核设计参数Table 1 Parameters of TMSR-SF1.

表2 组件计算时燃料区截面及四因子对比Table 2 Comparison of cross sections and four factors of the active core region.

控制棒的插入会压低反射层中的热群通量，同等功率下，增加堆芯中心通量，如图4所示，图4中T1-T3为图1所示不同方位角方向。由图4可知，TWOTRAN计算的通量分布在控制棒拔出和插入时不同方位角方向都符合良好，进一步说明本文所采用的SRAC-TWOTRAN对控制棒区域精细建模的准确性。控制棒的插入使得热中子泄漏由净入变为净出，即增加了燃料区泄漏，形象地反映了表2的不泄漏概率计算结果。控制棒拔出时，控制棒区为熔盐填充，由于熔盐对中子吸收，使得T1方位角方向在棒孔位置通量变低。

图4 组件计算在不同方向上的径向热群通量分布Fig.4 Radial thermal flux distributions in different azimuths.

5 SM-SPH方法在全堆模型计算中的应用

组件计算模型相当于控制棒全插，除了组件计算，本节还使用SM-SPH方法用于部分控制棒插入的全堆模型计算，并与SN输运参考解对比。首先进行三类组件计算，再进行二维堆芯（1/2堆芯）下单根控制棒计算及不同间距下的三根控制棒模型计算，主要是为了更好地验证棒间干涉效应。为了节省SN输运参考解的计算时间，1/2堆芯建模时省略掉不插棒的棒孔结构。同时，也采用常规的SPH方法与之对比。

5.1 部分控制棒插入全堆模型介绍

部分控制棒插入全堆模型如图5所示的1/2堆芯，无棒的棒孔全部省略，下边界为反射边界条件。单根控制棒模型在1/2堆芯中即在边界上构建半根控制棒。三根控制棒模型又根据1/2堆芯中两棒的不同棒距分为7个模型，即1/2堆芯中，半根控制棒（棒1）固定不动，所构建的完整控制棒（棒2）依次移动到如图5所示的7个完整棒位(Rod Position, RP)中，并编号为“三棒堆芯1-7”。

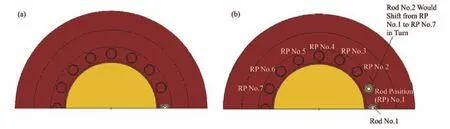
图5 部分控制棒插入全堆模型介绍 (a) 单根控制棒模型，(b) 三根控制棒模型Fig.5 Full core models with partial control rods inserted. (a) Core with one rod, (b) Core with three rods

5.2 三类组件计算

为了准确计算部分控制棒插入的1/2堆芯模型，划分三类组件（图1所示的1/32堆芯）：无棒孔组件；控制棒拔出组件；控制棒插入组件。其CITATION模型如图6所示的Theta-R模型，水平方向为Theta，垂直方向为R，并给出粗网间距，带灰色的每个区域对应于CITATION中的Zone。组件价值计算结果如表3所示。keff计算最大偏差为0.06%。SPH方法的价值偏差为0.236%，SM-SPH计算的价值偏差为0.348%，说明SM-SPH方法与SPH方法都能较好地反应出控制棒价值。三类组件使用不同方法得到的径向热群通量分布如图7所示。SM-SPH模型与SPH模型所计算的热群中子径向通量分布都与输运参考符合良好，包括控制棒强吸收体附近的不同方位角方向的通量分布。表4给出了体积通量权重方法用于控制棒插入组件得到的keff、强吸收体附近区域吸收反应率及泄漏率结果，并与参考解进行了对比。VFM方法得到的keff约偏大1%，吸收反应率偏低4.50%，泄漏率偏低达12.42%，说明使用VFM处理强吸收体时并不能保证反应率守恒。SPH模型和SM-SPH模型由于SPH因子的引入，只要SPH因子收敛，其相关反应率必然守恒。说明在组件层面上，SPH模型和SM-SPH模型通过引入SPH因子确保反应率守恒下都能得到接近参考输运解的结果。

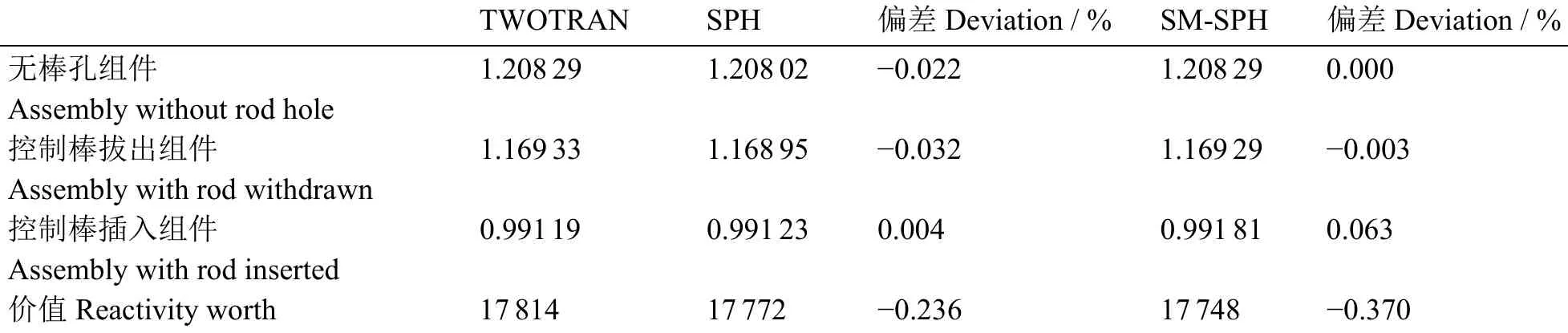
表3 三类组件keff计算结果Table 3 keff results of three kinds of assemblies.

表4 控制棒插入组件使用体积通量权重方法的结果Table 4 Results from volume-flux weighted method for assembly with rod inserted.

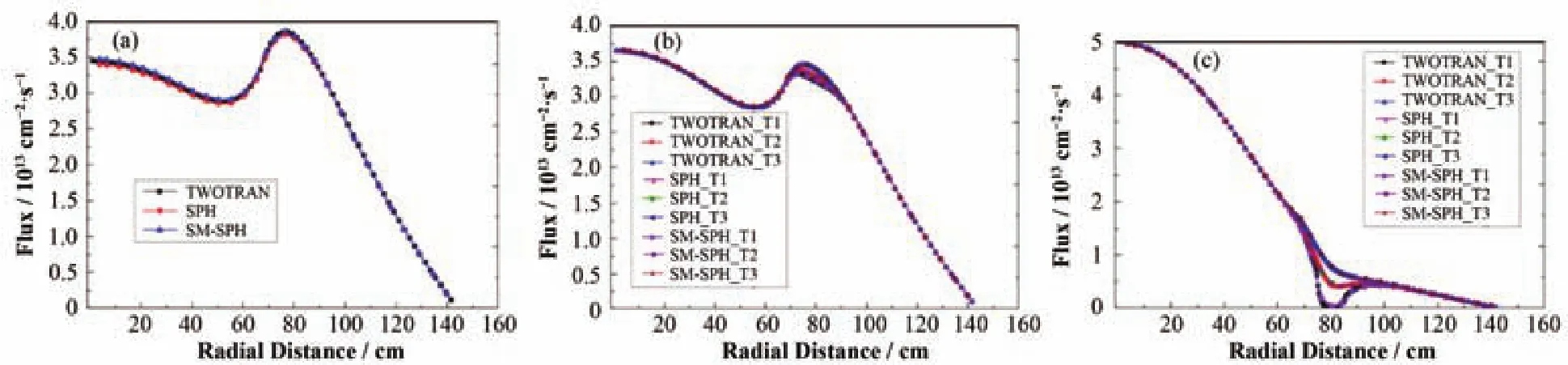
图7 三类组件径向热群通量分布 (a) 无棒孔组件，(b) 控制棒拔出组件，(c) 控制棒插入组件Fig.7 Radial thermal flux distributions of three kinds of assemblies. (a) Assembly without rod hole, (b) Assembly with rod withdrawn, (c) Assembly with rod inserted

5.3 部分控制棒插入全堆模型

对于单棒堆芯模型，其CITATION建模如图8所示。SPH模型由上述控制棒拔出或插入组件与无棒孔组件构成，构成整个1/2堆芯。SM-SPH模型的SPH区域的截面来源于组件计算的SPH因子修正的截面，而其他区域（包括燃料）采用谱修正计算。单棒下的控制棒价值计算结果如表5所示。参考解的单棒控制棒价值为1.704×10-2，SM-SPH及SPH模型计算的价值与参考解相差在4×10-4以内，偏差约2%。其插棒情况下燃料区最大功率密度分布偏差在1.2%以内。单棒堆芯模型下径向热群通量分布对比如图9所示，三者符合较好，与SPH模型相比，SM-SPH模型的通量分布与参考解符合更好。表6给出了单棒下强吸收体附近区域（图8(a)中的7-15）反应率对比。与参考解相比，SM-SPH及SPH模型计算的吸收反应率及泄漏率不再守恒，原因是单棒堆芯模型与进行SPH因子计算时的控制棒插入组件模型明显不同，但它们的偏差并不大（最大为2.60%），由于SM-SPH的泄漏率偏差较SPH的更小，且采用谱修正方法处理燃料区域，使得SM-SPH模型的通量分布与参考解符合更好。

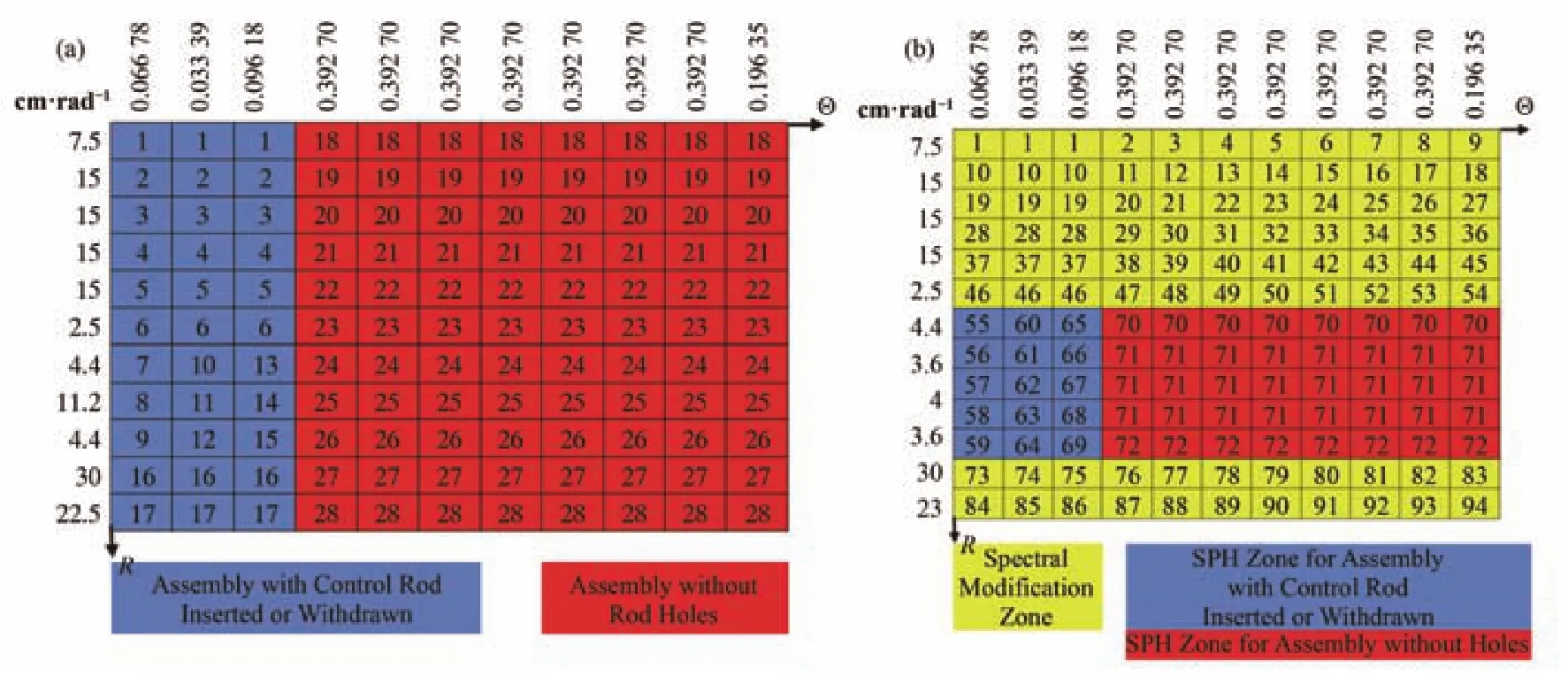
图8 单棒堆芯CITATION建模 (a) SPH模型，(b) SM-SPH模型Fig.8 CITATION models of core with single rod. (a) SPH model, (b) SM-SPH model

表5 单棒下的控制棒价值计算结果Table 5 Control rod worth results of core with single rod.

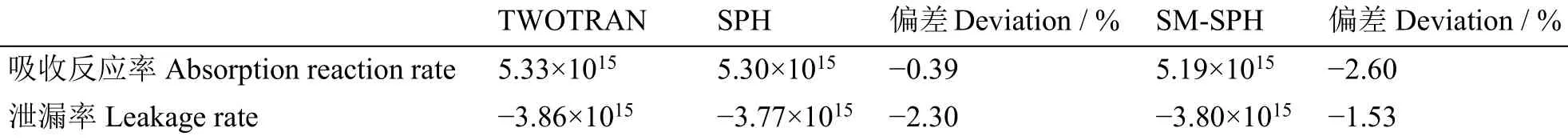
表6 单棒下强吸收体附近区域反应率对比Table 6 Comparison of reaction rates of strong absorber surrounding regions in core with single rod.

图9 单棒模型下径向热群通量分布对比Fig.9 Radial thermal flux distributions of core with single rod.

对于三棒堆芯模型，其建模与单棒堆芯模型类似。其价值计算结果如表7所示。从堆芯1到堆芯7，三棒的总价值先升后降，反映出了棒间干涉效应，堆芯1中三根棒紧挨，这时有最低价值3.243×10-2，而对于堆芯5，三根控制棒间距很大，相互之间的干涉影响很小，达到最大价值5.741×10-2。SPH模型计算结果堆芯1价值偏差最大，达到6.29%，而SM-SPH模型计算的价值最大偏差为1.524%（堆芯4），明显优于SPH模型计算。堆芯1下SPH模型功率分布最大偏差为6.09%，而SM-SPH模型功率分布最大偏差为1.08%。图10给出堆芯1与堆芯4的两根控制棒对应方位角方向上的径向热群通量分布。对于堆芯1，SM-SPH模型较SPH模型能更好地符合输运参考解。对于堆芯4，三棒的棒间距大于热中子扩散长度，相当于上述计算的单棒模型，SPH模型与输运参考解会存在一些偏差，而SM-SPH模型则与参考解符合良好。

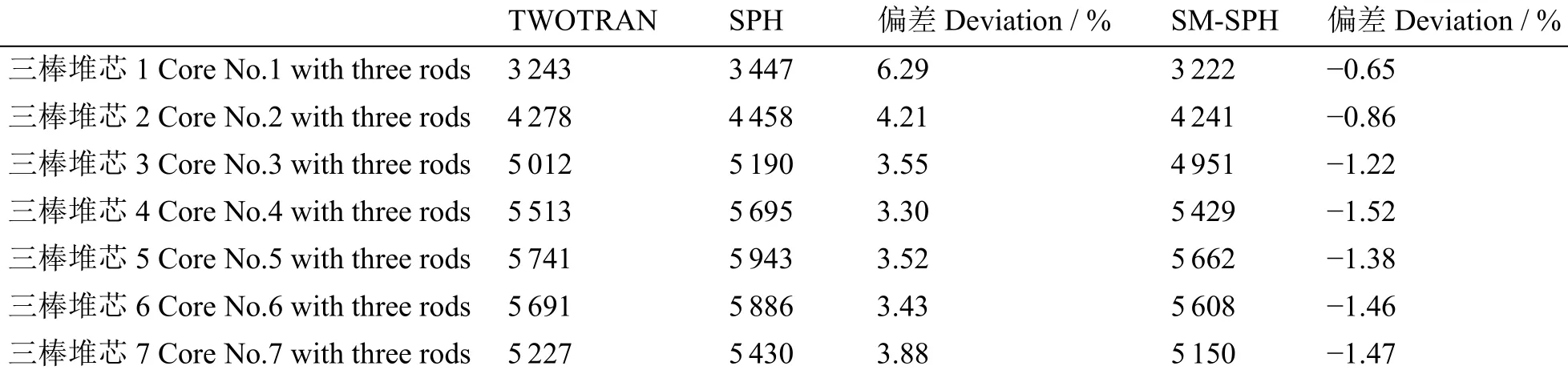
表7 三棒堆芯模型不同棒间距下控制棒价值计算Table 7 Control rod worth of cores with their rods.

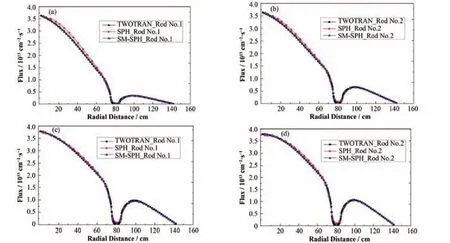
图10 三棒堆芯1 (a、b)与三棒堆芯4 (c、d)的两根控制棒对应方位角方向上的径向热群通量分布Fig.10 Radial thermal flux distributions of two rods in core 1 (a, b) and core 4 (c, d) with three control rods.

针对三棒堆芯1，本文给出了强吸收体附近区域的反应率及控制棒所在方位角对应的燃料区相对功率密度分布对比，分别如表8和图11所示。表8中反应率不再守恒，且吸收率相差很大(-27.62%)，但泄漏率偏差不大(3.00%)，这说明由组件计算得到的SPH因子并不能保证三棒堆芯1下吸收率守恒，但可以一定程度上确保泄漏率偏差不大，这可能是由于泄漏率是区域净中子流，取决于区域边界中子通量密度梯度，把强吸收体区域细分为多个区域且包括附近非强吸收体材料，一定程度上可以保证区域边界中子通量密度分布。对堆芯反应性及通量密度分布有影响的是强吸收体附近区域的泄漏率，对其吸收率并不需要太关心，甚至可以把反射层中强吸收体区域当黑体材料处理，只要能提供合适的黑体材料的拓展边界系数[12]。SPH和SM-SPH模型的反应率与参考解的偏差基本相似，图11中的SPH模型计算的燃料区相对功率密度最大偏差达到了6.09%，而SM-SPH模型的最大偏差为0.94%，说明在燃料区使用谱修正方法能极大改善控制棒对燃料区的影响。这是因为SPH模型中包括燃料的所有区域的截面都来自于组件计算（控制棒全插）结果，而SM-SPH模型中只有强吸收体附近区域的截面来源于组件计算，从而不会明显受制于组件计算时所采用的边界条件，可以通过谱修正方法反馈强吸收体附近区域的泄漏率来修正谱区截面，从而使得SM-SPH模型能更好地处理棒间干涉效应。

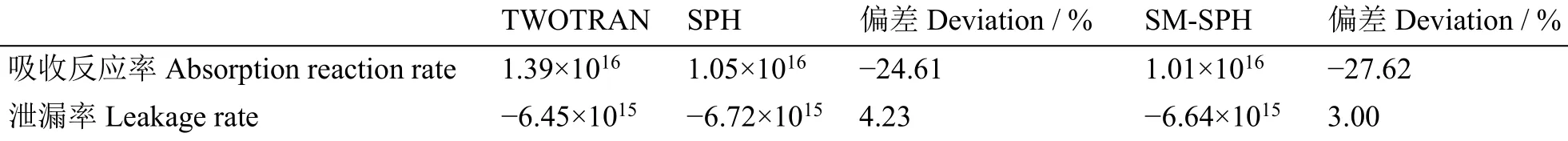
表8 三棒堆芯1强吸收体附近区域反应率Table 8 Comparison of reaction rates of strong absorber surrounding regions in core 1 with three control rods.

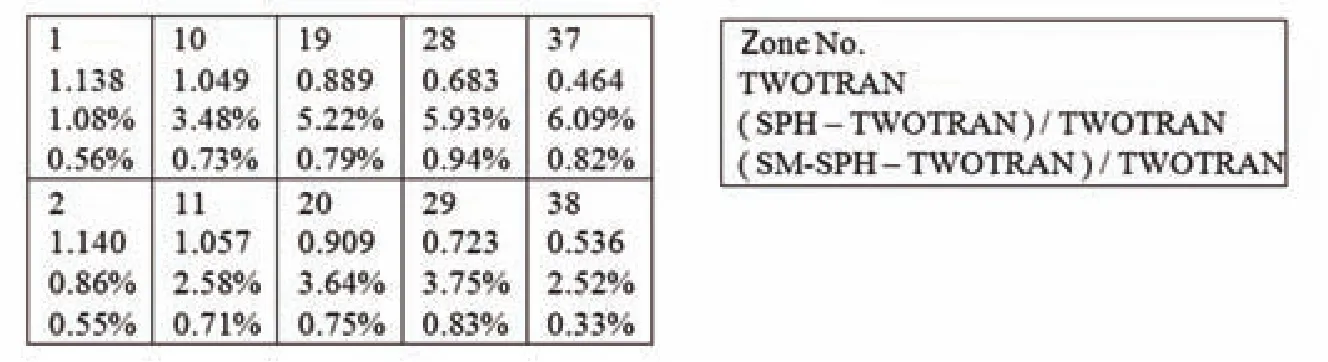
图11 三棒堆芯1控制棒所在方位角对应的燃料区相对功率密度分布对比Fig.11 Comparison of relative power densities of fuel zones to which control rods corresponds in azimuth direction in core 1 with three control.

6 结语

本文针对PB-FHR中控制棒价值计算难点，研究了SPH方法应用于反射层中控制棒价值计算模型，提出SM-SPH模型，即把谱修正方法与SPH方法相结合，通过迭代方法求解强吸收体区域附近的SPH因子。计算表明，该模型能有效地计算控制棒价值及通量分布，并且较常规的SPH方法能更好地处理棒间干涉效应。SM-SPH方法首先通过组件计算得到强吸收体附近区域的经过SPH因子修正的截面，然后采用谱修正方法处理其他区域截面，从而可以实现带控制棒的三维堆芯扩散计算。

1 Forsberg C W, Peterson P F, Kochendarfer R A. Design options for the advanced high-temperature reactor[C]. Proceedings of ICAPP’08, Analeim, CA, USA, June 8-12, 2008.

2 孙建友, 邹杨, 严睿, 等. 球床氟盐冷却高温堆中6Li摩尔浓度对冷却剂温度反应性系数影响的研究[J]. 核技术, 2014, 37(9): 090605. DOI: 10.11889/j.0253-3219. 2014.hjs.37.090605. SUN Jianyou, ZOU Yang, YAN Rui, et al. Analysis of the coolant reactivity coefficients of FHRs with6Li contents of coolant[J]. Nuclear Techniques, 2014, 37(9): 090605. DOI: 10.11889/j.0253-3219.2014.hjs.37.090605.

3 孙建友, 邹杨, 严睿, 等. PB-FHR堆芯活性区体积对冷却剂温度反应性系数影响的研究[J]. 核技术, 2014, 37(12): 120603. DOI: 10.11889/j.0253-3219.2014.hjs.37. 120603. SUN Jianyou, ZOU Yang, YAN Rui, et al. Study on the influence of core volume of PB-FHR on coolant temperature reactivity coefficient[J]. Nuclear Techniques, 2014, 37(12): 120603. DOI: 10.11889/j.0253-3219.2014. hjs.37.120603.

4 Zhu G, Zou Y, Xu H, et al. Uranium utilization with thorium blanket in pebble bed fluoride salt-cooled high temperature reactor[J]. Progress in Nuclear Energy, 2015, 83: 374-386.

5 许云林, 经荥清, 王德安. 10 MW高温气冷堆反应性当量计算[J]. 核动力工程, 1997, 18(6): 500-504. XU Yunlin, JING Xingqing, WANG Dean. Reactivity worth calculation for control rods of high temperature gas-cooled reactor[J]. Nuclear Power Engineering, 1997, 18(6): 500-504.

6 郭炯, 李富, 王登营. 高温气冷堆控制棒区等效截面方法的改进[J]. 核动力工程, 2010, 32(S2): 128-131. GUO Jiong, LI Fu, WANG Dengying. Treatment and improvement of equivalent cross sections in control rod region for high temperature gas-cooled reactor[J]. Nuclear Power Engineering, 2010, 32(S2): 128-131.

7 周旭华, 李富, 王登营, 等. 高温气冷堆控制棒区不连续因子的计算与应用[J]. 核动力工程, 2008, 29(6): 1-5. ZHOU Xuhua, LI Fu, WANG Dengying, et al. Calculation and application of discontinuity factors in control rod region for high temperature gas-cooled reactor[J]. Nuclear Power Engineering, 2008, 29(6): 1-5.

8 Alain Hébert. Applied reactor physics[M]. Ottawa: Presses Internationals Polytechnique, 2009: 247-253.

9 Mphahlele R, Ougouag A M, Ivanov K N, et al. Spectral zone selection methodology for pebble bed reactors[J]. Annals of Nuclear Energy, 2011, 38(1): 80-87.

10 戴明, 朱贵凤, 戴叶, 等. 基于CITATION-ORIGEN2球床堆平衡态计算程序的实现[J]. 原子能科学技术, 2017, 51(1): 113-119. DAI Ming, ZHU Guifeng, DAI Ye, et al. Burnup calculation for equilibrium cycle of pebble-bed reactor with CITATION-ORIGEN2 codes[J]. Atomic Energy Science and Technology, 2017, 51(1): 113-119.

11 李满仓, 王侃, 姚栋. 基于连续能量蒙特卡罗方法的均匀化群常数计算[J]. 核科学与工程, 2012, 32(4): 306-314. LI Mancang, WANG Kan, YAO Dong. Continuous energy Monte Carlo method based homogenization multi-group constants calculation[J]. Nuclear Science and Engineering, 2012, 32(4): 306-314.

12 Okumura K. COREBN: a core burn-up calculation module for SRAC2006[R]. Ibaraki-ken: Japan Atomic Energy Agency, 2007: 6-7.

第十二届中国核电技术发展高峰论坛在沪顺利召开

由上海市核电办公室支持，比利时诺本集团承办的“第十二届中国核电技术发展高峰论坛”于2017年8月31日在上海浦东华美达酒店成功召开，来自国内外政府机构、核电投资方、运营方、核电建设公司、领先的核电设备制造商等百余位领导和专家出席了本届论坛。上海市核电办公室主任韦平出席会议并发表致辞，《核技术》作为媒体合作伙伴到会展示了期刊宣传页、样刊和核能栏目近三年发表的文章目录，受到与会代表的欢迎。

本次大会的演讲嘉宾有国家核电副总经理、国家电投海外投资公司董事长侯学众，华龙国际核电技术有限公司副总经理兼总工程师咸春宇，法国驻华大使馆核参赞Dominique OCHEM，英国驻华大使馆英国国际贸易部（商务处）能源主管、商务参赞Catriona KNOX，中国原子能科学研究院副院长刘森林，中国核工业第五建设有限公司副总工程师、研究员级高级工程师刘卫华，中核瑞能有限公司战略信息部副经理张琦。

嘉宾们就“一带一路”背景下中国核电“走出去”、中法核燃料循环合作项目、中英民用核电领域合作、中国核循环产业发展等热点话题发表了精彩演讲。

小组讨论精彩纷呈，围绕“华龙一号”的融合方案进展和“三代核电技术”批量化建设前景展望等主题，由中广核研究院的副总工程师周跃民主持，嘉宾包括：国家核电国际业务部总经理王晓航、华龙国际核电技术有限公司副总经理兼总工程师咸春宇、广西防城港核电有限公司副总经理宫广臣和中国原子能科学研究院副院长刘森林等。

此外中国核工业建设集团公司、中国国电集团有限公司、中核核电运行管理有限公司、广西防城港核电有限公司、江苏核电有限公司、国核示范电站有限公司、大唐华银电力股份有限公司、中国第一重型机械股份有限公司、东方电气集团、上海电气集团、中广核研究院、上海核工程研究设计院、国家电投集团科学技术研究院、中国能建广东省电力设计研究院、华东电力设计院等单位的领导及专家作为特邀嘉宾出席了会议。一年一度的诺本核电论坛在热烈的气氛中圆满结束。

Super homogenization method applied in diffusion calculation for pebble-bed fluoride-salt-cooled high-temperature reactors

DAI Ming1,3ZHU Guifeng1,2DAI Ye1,2ZOU Yang1,2YU Xiaohan1,2

1(Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Jiading Campus, Shanghai 201800, China) 2(Key Laboratory of Nuclear Radiation and Nuclear Energy Technology, Chinese Academy of Sciences, Shanghai 201800, China) 3(University of Chinese Academy of Sciences, Beijing 100049, China)

Background： The control rods of pebble-bed fluoride-salt-cooled high-temperature reactor (PB-FHR) are located in the side reflector. Neutron diffusion calculation in those control rods has difficulties of no fission source in the control rod region and strong effect from the core leakage spectrum. Purpose： This study aims to apply super homogenization (SPH) method in diffusion calculation for PB-FHR. Methods： SPH method is applied in the diffusion calculation for the strong absorber in control rod region located in the reflector area of the PB-FHR, through which the local area of control region is homogenized. The spectra of different places of the reactor core except the control rod region are calculated to modify its cross sections. SPH factors calculation is accomplished by an iteration procedure between SPH and spectra modification (SM). Results： Reactivity worth of the control rod and neutron flux distribution are calculated accurately. Conclusion： Compared with the fine mesh transport reference solution, the verification results demonstrates that the method proposed can accurately model the control rod including the reactivity worth and flux distribution, and it is more suitable for the situation with interference effect between different control rods compared with regular SPH method.

PB-FHR, Control rod, SPH, Strong absorber

DAI Ming, male, born in 1988, graduated from Central South University in 2011, doctoral student, focusing on nuclear reactor physics Corresponding author: YU Xiaohan, E-mail: yuxiaohan@sinap.ac.cn

date: 2017-03-14, accepted date: 2017-05-27