基于身份的在线电子现金系统设计
2017-09-18陈轶群
陈轶群

摘要: 本文在了解并分析国内外的盲签名技术应用现状和发展趋势,特别是基于身份的部分盲签名技术方案的基础上设计并实现了基于身份的在线电子现金系统。作者设计实现了在电子支付流程中3个身份主体(用户、银行、商家)间4个主要过程:开户注册、提取现金、用户消费、银行支付。最后对本文工作进行了总结并展望系统的发展。
关键词: 基于身份的密码体制; 电子现金; 部分盲签名
中图分类号:TP309.7
文献标志码:A
文章编号:2095-2163(2017)04-0027-04
0引言
电子现金(e-cash)是数字时代的产物,是真实现金的数字化模拟,具有真实世界中现金的一些特性。电子现金一般也假设了一个权威机构,该机构负责把真实的货币和电子现金联系起来,或者单独发行电子现金。因此有些电子现金系统中权威机构每发行一笔电子现金给用户,还会从用户的账户中扣除一部分真实货币,这样保证了电子现金的发行不会干扰真实世界中纸币的发行总量。在有些电子现金系统中,权威机构是单独发行电子现金的,这种电子现金不与真实的货币产生关联,而是作为一种独立存在的货币形式,在考虑发行总量等因素时,需要核算这一部分单独发行的电子现金。
本文所研究的电子现金系统,设有权威机构,且可以发行单独的电子现金,也可以发行与真实货币相关联的电子现金。采用盲签名技术使得所发行的电子现金与用户的身份没有关联,能够保护用户的隐私。同时通过在线数据库的查询保证了电子现金不会被重复消费。而部分盲签名技术则帮助缩小了数据库的规模。采用了基于身份的技术使得该系统的部署更为简单,不依赖公钥基础设施。
1在线电子现金系统
电子现金系统存在4个过程:注册、提现、消费、银行支付。一般包含3个主体:用户(U)、商家(M)和银行(B),在有些电子现金系统中还存在一个可信第三方(T)。一个理想的电子现金系统应具有以下的优点[1]:
1)[JP3]匿名性。如同现实世界,现金的使用不泄漏用户的身份。[JP]
2)不可伪造性。用户不能伪造电子现金。
3)不可重复花费性。电子现金只能使用一次,重复花费将以很大的概率被发现。
4)可分性。电子现金可以分成数额更小的现金,但总金额保持不变。
5)不可联结性。用户不同的电子现金不能被联接起来。
电子现金系统按照其交易的载体可分为:基于账户的电子现金系统和基于代金券的电子现金系统。前者类似于支票、电话卡等,已经普遍使用;后者类似于普通的现金,由于其匿名性、安全性等各方面的原因尚未使用。
按花费时商家是否与银行进行联机验证可分为:在线的电子现金系统和离线的电子现金系统。由于在线系统在提取、消费、银行支付三个阶段都需要和银行进行通信,银行容易成为系统的瓶颈,降低系统的效率;而离线系统不需要银行即时验证,所以可能存在多重花费的问题。
2基于身份的密码体制及部分盲签名
2.1基于身份的密码体制
在传统的基于证书的公钥密码系统中,当用户的数量很大时,密钥管理和撤销工作将会非常复杂,并且需要大量的密钥和证书存储空间。为了简化PKI的密钥管理程序,1984年,Shamir首次提出了基于身份的密码体制思想。
基于身份的密码系统总是包含有一个私钥产生中心和许多用户。私钥产生中心PKG(Private Key Generator)是一个可信赖机构,负责对系统进行初始化,用户向其提交身份信息,PKG再返回用户相应的私钥。基于身份的密码系统的实质就是选取用户的身份信息,如电子邮件地址或邮政地址来充当用户的公钥,换句话说,用户的公钥可直接由其对应的身份信息计算出来。而只有PKG可以计算出用户的私钥。在这种体制下,用户不再需要公钥证书也不需事先验证通信方的公钥的有效性,从而提高了系统的效率及系统的安全性。
基于身份的密码体制可以通过椭圆曲线上的双线性对来设计实现。下面给出双线性对的数学定义和性质:
[JP2]假定G1是椭圆曲线上一个素数q阶循环加法群其成员为P,G2是一个q阶循环乘法群。在集合G1和G2上的離散对数问题是难解的。一个双线性对是一个映射e〖DD(-*1〗[WT6BX]^〖DD)〗[WT5”BX]:G1×G1→G2且满足以下3个基本属性:[JP]
1)双线性:对所有P,Q,R∈G1,e〖DD(-*1〗[WT6BX]^〖DD)〗[WT5”BX](P+Q,R)=e〖DD(-*1〗[WT6BX]^〖DD)〗[WT5”BX](P,R)e〖DD(-*1〗[WT6BX]^〖DD)〗[WT5”BX](Q,R),并且e〖DD(-*1〗[WT6BX]^〖DD)〗[WT5”BX](P,Q+R)=e〖DD(-*1〗[WT6BX]^〖DD)〗[WT5”BX](P,Q)e〖DD(-*1〗[WT6BX]^〖DD)〗[WT5”BX](P,R)。
2)非退化性:存在P,Q∈G1,使得e〖DD(-*1〗[WT6BX]^〖DD)〗[WT5”BX](P,Q)≠1。
3)可计算性:对任给的P,Q∈G1,存在有效的算法计算e〖DD(-*1〗[WT6BX]^〖DD)〗[WT5”BX](P,Q)。
2.2基于身份的部分盲签名
基于身份的部分盲签名方案包含一个可信的密钥分发中心(PKG)、一个签名人和一个接收方。接收方和签名方就签名的部分消息达成一致,允许接收方隐瞒另外一部分消息。签名人只知道部分内容的消息签名。一个具体的部分盲签名方案包含4个算法:参数设定(Setup)、密钥生成(KeyGen)、分发(Issue)和验证(Verify)。其中分发算法是一个交互式协议,在签名人和接收方之间运行,包含额外4个子算法:协商(Agree)、盲化(Blind)、签名(Sign)和去盲(Unblind)。在此可展开论述如下。endprint
1)Setup:由PKG运行。输入安全参数k,生成公开的参数params,包含签名空间、消息空间、公共消息空间,另外生成秘密的PKG的主私钥s。
2)KeyGen:输入签名人的身份字符串ID,PKG使用其私钥s,公开参数params,计算签名人的签名密钥SID。
3)Issue:假设接收方所希望签署的消息是m,在执行以下的4步后,会生成关于m的一个签名δ。如果没有输入公共消息,在执行以下的4步后也会生成一个公共消息c。这里,将给出步骤内容依次分述如下。
① Agree:如果没有输入公共消息,接收方和签名人交互生成公共消息c。
② Blind:该算法输入随机字符串r、消息m、公共消息c,输出字符串h,发送给签名人。
③ Sign:该算法输入签名人的私钥sk、字符串h、输出签名δ〖DD(-*2〗-〖DD)〗,发送给接收方。
④ UnBlind:该算法输入签名和Blind步骤中的随机字符串r,输出去盲的签名δ。
4) Verify:该算法输入去盲的签名δ、消息m、公共消息c、签名人的身份字符串ID, 输出“真”或者“假”,表示签名是或者不是一个有效的签名,这种有效性是指是否是签名人用私钥SID对消息m和公共消息c生成的签名。
[JP2]一个安全的部分盲签名方案需要具有2个基本的安全属性,一个是不可伪造性,一个是部分盲性。其中,不可伪造性是一种在适应性选择消息和身份的条件下存在性的不可伪造。[JP]
直观来看,部分盲签名的不可伪造性保证了攻击者在不能生成签名人私钥的情况下,将无法生成有效的该签名人签署的部分盲签名。
而关于部分盲性的描述如下。在典型的盲签名中,签名人完全不知道签署的消息。如果签名人能够把签署的某个数字签名和某次具体的签署过程联系在一起,盲签名的盲性就失效了。对比来看,部分盲签名中,签名人和接收人需要预先确认一个公共消息。如果签名人在公共消息中嵌入一个独特的可识别的信息,那么签名人就很容易地把签名和某次签名的过程联系起来,因此也就没有了盲性。为了使部分盲签名有意义,公共消息空间的大小应该远小于全部的签名请求的数量。部分盲签名的这种弱点是天生的,是为在消息中嵌入公共消息所付出的代价。
直观来看,部分盲签名的盲性就是让签名人不能知道自己所签署的数字签名和哪一个去盲化之后的消息对应。这里可以明确地看到,公共信息对所有部分盲签名形成了一种简单的划分,在每一个子划分内,签名人是完全盲的。
3基于身份的在线电子现金系统
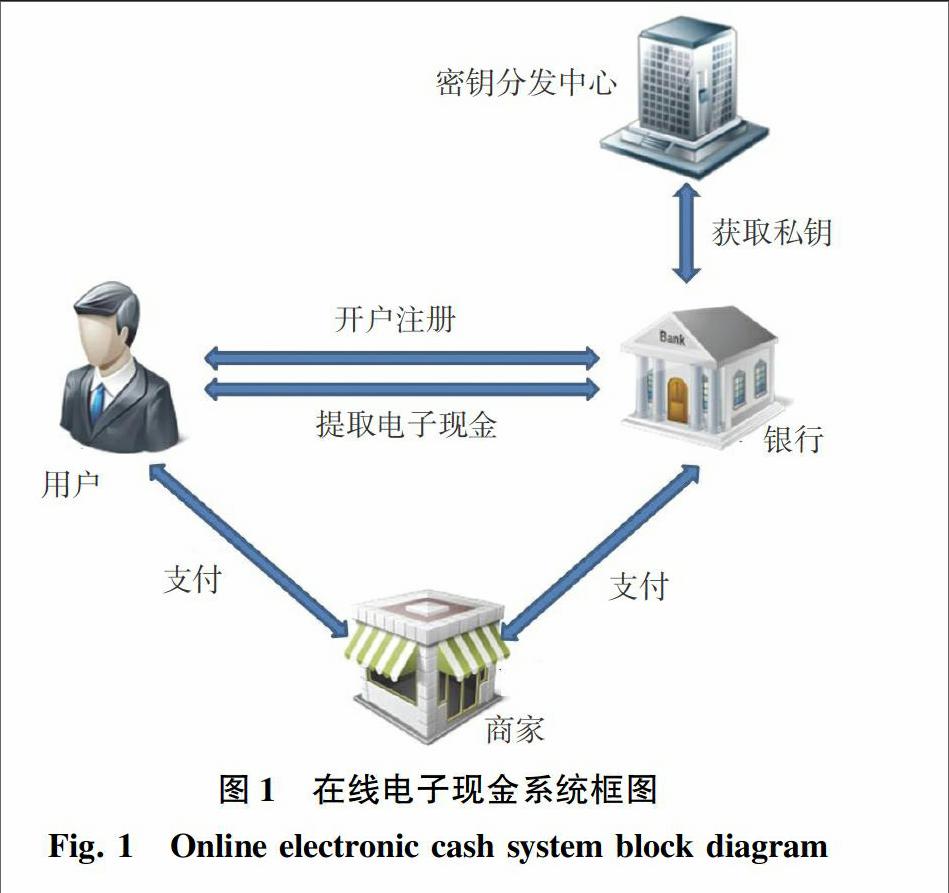
本系统包含4个基本过程和4个参与方,如图1所示。
4个参与方包括可信任的密钥分发中心(PKG)、银行(Bank)、商家(Shop)和用户(User)。其中PKG和银行间有一个交互过程(KeyGen),该过程结束后银行可获得以其域名为身份的私钥。在研发时,PKG可以是银行所有(国内主要商业银行自己建立PKG),也可以单独实现。用户和银行间有2个基本过程,分别是:开户注册(Reg.)和电子现金提取(Withdrawal)。开户注册过程确认通过后,用户将获得一个电子现金账号,银行则记录该账号和用户的身份。电子现金提取过程全部展开执行后,用户即获得银行使用其私钥签署的电子现金。用户、商家和银行将协同参与一个基本过程,也就是支付(Pay)过程。支付过程完成后,商家获得现金,银行向商家支付,记录已经消费的电子现金。下面即按照不同的参与方来探讨各参与方的功能和参与方之间的基本交互过程。
3.1密钥分发中心模块设计
密钥分发中心(PKG)可重点实现整个系统的参数生成,为自己生成公钥和私钥,对每一个请求私钥的实体进行验证,并生成私钥。典型地,PKG包括2个主要模块。一个是参数设定模块,生成自己的公私钥;一个是密钥生成模块,为用户的身份字符串生成私钥。一个设计完善的PKG还应该包括注册模块、执行策略模块等。本文仅针对主要模块,提出详尽应用探讨解析如下。
3.1.1参数设定模块
本系统采用了PBC库的A类型参数。其中q是大素数,满足模4余3。E是椭圆曲线y2=x3+ax,其中a可以取值为-3。那么E(Fq)是一个超奇异椭圆曲线,椭圆曲线上离散点的数目为q+1,且對应定义在Fq2上的椭圆曲线的点的数目为(q+1)2。进一步,对任意整除q+1的奇数r,椭圆曲线E(Fq)上的离散点构成一个r阶的循环群,嵌入指数是2。
在本系统开发过程中,研究使用了PBC库自带的A类型参数(q、h、r),这些参数确定了椭圆曲线上的群G+,G2和对运算e〖DD(-*1〗[WT6BX]^〖DD)〗[WT5”BX](·,·)以及阶q(r)。其它的参数还包括G+的生成元P和杂凑函数H(·)、H0(·)。其中,生成元通过随机选择G+中的点来设定。而杂凑函数通过使用SHA-256来实现,对于映射到椭圆曲线上的杂凑函数,在SHA-256之后使用了PBC库的element_from_hash函数来提供设计支持。PKG的私钥s通过从Zr中随机选择得到,而公钥Ppub使用element_pow_zn计算求出。PKG的公钥和私钥分开存储在2个独立的文件中。
3.1.2密钥生成模块
该模块要求用户输入自己的ID字符串,回车后为用户生成对应于该ID的私钥。在此基础上,更为完善的模式构建可设计描述为:首先检查用户的ID,确认用户的身份,之后将ID与日期等信息绑定,形成一个在一定期限内有效的ID,以便能够处理用户吊销身份的事件。本系统仅实现了核心的功能,并采取了简单的DOS界面方式,具体即如图2所示。
该模块的内部执行方式与第2节研究设计的部分盲签名的KeyGen算法相同,首先把用户输入的ID字符串进行SHA-256的杂凑,之后使用PBC库的element_from_hash函数把用户的ID字符串映射为椭圆曲线上的一个点,最后使用element_pow_zn输入PKG的私钥s计算用户的私钥sID。该私钥存储在单独的文件中,面对面、或者通过安全信道交给用户。endprint
3.2银行功能模块设计
银行一方面与PKG交互获得私钥,一方面与用户交互,为用户配置了注册、电子现金提取,并有效参与了支付过程。其中,银行与PKG的交互过程按照PKG的密钥生成模块来执行。其它3个功能分别叙述如下。
3.2.1开户注册
研究假设用户已经在其智能手机上安装了银行的APP,并且与银行能够建立安全连接,银行能够通过账户、密码、USB KEY等方式确认用户的合法身份。用户打开银行APP并启用身份认证,打开电子现金注册功能,该软件生成该用户的私钥和公钥。也就是通过使用了PKG生成的系统参数来为用户生成公私钥,其过程与PKG建立自己的主密钥对的过程类似。需要注意的是,当前的执行主体是用户,生成的私钥由用户保存,而公钥则由APP反馈给银行,银行存储公钥信息、并和用户的身份绑定。对于设计完善的应用程序,在此步骤则应额外返回银行一个知识证明,证明用户确实拥有对应的私钥。
3.2.2电子现金提取
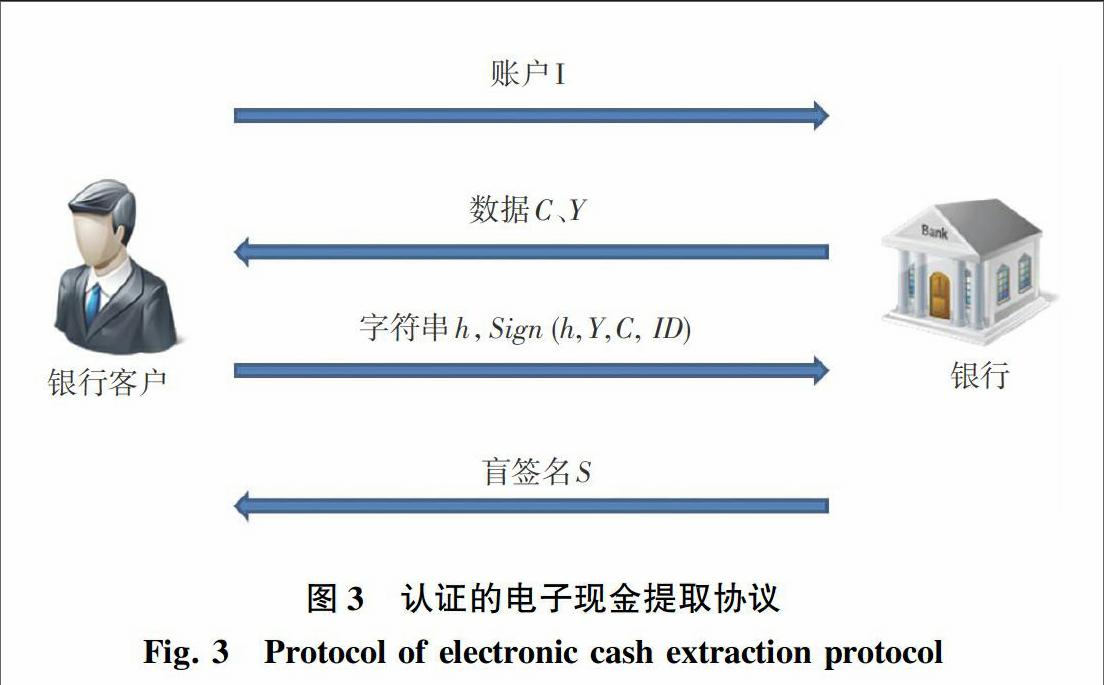
通常,电子现金提取包括用户证明自己拥有某个账号的认证流程和提取电子现金的内容,这里把这2个部分整合在一起,并给出直观设计展现如图3所示,即使银行和用户协同执行如下“认证的电子现金提取协议”:
1)首先,用户的APP向银行发起请求,要求提取电子现金;该消息包含用户的账户信息或者其摘要的信息。
2)银行核实账户I确实是自己的用户,就按照Chow等人的部分盲签名方案[2],计算Issue算法中Sign-1的子步骤,获得C、Y。这2个数据发送给用户的APP,兼有单向认证协议的挑战消息的功能。
3)用户的APP按照Chow等人的部分盲签名[2],计算Issue算法中Blind的子步骤,获得h,然后使用ISO标准化版本中的“使用公钥的2次传输单方认证协议”,构造签名,共同返回给银行。
4)银行使用用户的账户信息I,验证用户的签名,验证通过后按照Chow等人的Issue算法[2]中Sign-2子步骤计算S,并返回给用户。
5)用户的APP按照Chow等人的Issue算法[2]中UnBlind子步骤去盲化,获得电子现金,并使用银行的ID验证电子现金的有效性。
上述认证的电子现金提取协议内嵌了一个ISO标准化版本中的“使用公钥的2次传输单方认证协议”,可以让银行切实掌控处理对用户的认证;而电子现金本身提供了用户对银行的认证,因此本质上实现了用户和银行之间的双向认证,并同时完成了电子现金的提取。
3.2.3支付过程
银行设计参与的支付过程是发生在银行与商家之间的。对于在线电子现金系统,这意味着商家每收到用户的“一张”电子现金,都需要交给银行验证真伪,并由银行返回验证的结果。本系统使用的是基本的Web-Service方式,即银行提供电子现金验证的Web方法。通过分析可知在.NET3.5框架下,使用Visual Studio 2008已经可以调动Windows Communication Foundation (WCF)功能了,该功能具备了WS-Security机制,可以保护商家和银行之间的通信的安全。
在Web-Service方式下,銀行仅仅完成验证功能。输入的参数包括消息、共享消息、签名字符串,返回电子现金是否有效的结果。为了在C#中使用PBC库,需要封装签名验证的功能到一个动态链接库(DLL),然后在C#中导入该DLL,引用签名验证的函数,获得验证结果。如果验证通过,银行搜索SQL数据库,如果数据库中没有存储该电子现金,说明电子现金有效,则向商家账户存入电子现金,返回给商家电子现金有效的信息,并存储该电子现金到数据库中;否则,将给商家返回无效的信息。
3.3商家功能模块设计
商家与用户交互,也与银行交互。研究假设商家拥有一个电子商务网站,这样,用户可以在该网站选择自己的商品,购物选择结束后,即使用电子现金支付。当然,商家也可以是一个实体的商店,但是需要拥有能够读取用户存储设备中电子现金的能力,例如通过近场通信技术(NFC),一个读卡器可以读取用户手机中存储的内容。对于本文的在线电子现金系统,设计中重点关注了商家的支付功能。假设用户通过商家的网站来进行支付,用户通过点击一个支付按钮完成支付。简单起见,研究中仅考虑了定额10美元支付的功能,也就是每次支付都是从用户“钱包”中读取“一张”电子现金。
3.4用户功能模块设计
用户与银行交互,也与商家交互。本文的电子现金系统中用户与银行的交互是通过用户的APP研发实现的,主要的功能包括开户和电子现金提取,与商家的交互主要是通过商家的网站设计得到的。但是智能完备的程序设计中,用户还要配备一个功能来管理自己的电子钱包,对存取行为进行授权,例如通过Windows的文件驱动来提供设计支持。上述的注册功能与银行交互,为用户生成一对公私钥,其中公钥是用户的电子现金账号,提交给银行。而电子现金提取功能,允许用户设置共享的消息,并完成与银行的“认证的电子现金提取协议”。
4结束语
本文研究综述了一个基于身份的电子现金系统的实现过程。该系统综合了客户与银行在提现阶段的认证和部分盲签名算法,给出了认证的电子现金提取协议,提高了效率;另外该系统采用了PBC库的“A”参数,保证了提现、消费等阶段的运算速度,提升了效率;最后,该系统采用URL地址做网上银行的身份,减轻了钓鱼网站的危害。
当然本系统还需要进一步的完善,包括:
1)支持离线的电子现金。为了支持离线的电子现金,需要修改电子现金系统的基本算法,在当前核心算法的基础上,进一步增加基于受限盲签名的实现代码,最终封装为可离线消费的电子现金系统。
2)支持客户端的钱包管理。一个完整的电子签名作为“一张”电子现金,以数据的方式存储在某个存储设备中,那么对该存储设备必须提供相应的访问控制的功能,也就是“钱包”管理。endprint
3)完善当前的各项设定功能。在本文的整体论述中,对每一个功能,都已明确指出了一个完善系统研究拓展的具体细节。本文设计实现的是一个较为简单的概念系统,因此后续研究应将相关的功能在进行有效改进升级后,才能够真正地投入现实使用。
参考文献:
[WTBZ][ST6BZ][HT6SS][1] [ZK(#〗
陈晓峰. 电子商务安全性的理论与技术研究[D]. 西安:西安电子科技大学, 2003.
[2] CHOW S S M , HUI L C K, YIU S M, et al. Two improved partially blind signature schemes from bilinear pairings[C]//ACISP 2005. Berlin: Springer, 2005,3574: 316-328.
[3] CHAUM D. Blind signature for untraceable payments[M]// CHAUM D, RIVEST R L, SHERMAN A T. Advances in cryptologyEurocrypt. US: Springer, 1983: 199-203.
[4] ABE M, FUJISAKI E. How to date blind signatures[M]//KIM K, MATSUMOTO T. Advances in CryptologyAsiacrypt 1996. Berlin: Springer,1996, 1163: 244-251.
[5] 許静,冯伟成,周莲英,等. 基于部分盲签名的新型电子现金安全系统研究[J]. 计算机工程,2006,32(19):157-158,175.
[6] 金鑫,疏国会. ActiveX控件应用安全研究[J]. 数字技术与应用,2011(8):241-243.
[7] ZHANG F, SAFAVI-NAINI R, SUSILO W. An efficient signature scheme from bilinear pairings and it's applications[M]// BAO F, DENG R, ZHOU J.Public key cryptographyPKC 2004. PKC 2004. Lecture Notes in Computer Science. Berlin: Springer,2004,2947:277-290.endprint
