浮式风力机多平台阵列的动态响应

丁勤卫， 李 春,2， 叶柯华， 郝文星， 叶 舟,2

(1. 上海理工大学 能源与动力工程学院， 上海 200093；2. 上海市动力工程多相流动与传热重点实验室， 上海 200093)

浮式风力机多平台阵列的动态响应

丁勤卫1， 李 春1,2， 叶柯华1， 郝文星1， 叶 舟1,2

(1. 上海理工大学 能源与动力工程学院， 上海 200093；2. 上海市动力工程多相流动与传热重点实验室， 上海 200093)

为研究浮式风力机多平台阵列的动态响应特性，建立了基于OC3-Hywind Spar Buoy平台的NREL 5 MW浮式风力机整机模型，根据辐射/绕射理论方法分别研究并比较了单平台、1×5线性排布和3×3方阵排布的多平台动态响应特性.结果表明：浮式风力机Spar平台在纵荡、垂荡和纵摇方向的响应均集中在低频波浪阶段；1×5线性排布的多平台纵荡位移响应均低于单平台，共用系泊系统有效抑制了平台的纵荡位移响应，但是对垂荡位移、纵摇偏转角响应影响不大；3×3方阵排布位于两侧的平台存在较大的横荡位移响应，但纵荡位移响应均小于单平台，位于中间位置的平台纵荡位移响应大于单平台，但横荡位移响应几乎可以忽略不计；3×3方阵排布中心位置和顶点处的平台垂荡位移、纵摇偏转角响应小于单平台，其余平台垂荡位移、纵摇偏转角响应没有受到明显抑制.

浮式风力机； Spar平台； 阵列； 动态响应

“由陆向海、由浅向深、由固定基础向漂浮式平台”已经成为未来风电场建设的必然趋势[1-3].与陆上风力机不同，海上漂浮式风力机(以下简称浮式风力机)在运行过程中始终需要承受波浪载荷的作用，因此载荷特性更加复杂.由于固有的摇荡特性，浮式风力机始终处于不平衡受力和非定常运动状态，类似这种交变载荷会加剧结构尤其是传动系统的疲劳、变形甚至破坏.与传统的海工石油平台相比，浮式风力机平台的重心位置更高，水线面面积矩更小，对波浪激励更敏感.因此，研究浮式风力机平台的动态响应对于海上风电场的安全运行具有重要意义.

与张力腿平台(TLP)、Barge平台相比，Spar平台具有低重心、高灵活性、低造价的特点[4].齐凯[5]以Cell Spar平台为研究对象，进行了模态与结构强度分析，得到了应力集中区域.刘毅[6]提出了一种结合风力机动态特性的结构强度分析方法，研究了简化为圆筒壁的NREL 5 MW Hywind单柱式浮式风力机，对其进行结构分析和强度校核.Ran[7]对Spar平台的系泊系统进行了耦合分析，研究不同形式Spar平台的运动响应以及影响平台运动性能的关键参数.王东华等[8]建立了基于OC3-Hywind Spar Buoy平台的NREL 5 MW浮式风力机整机模型，采用辐射/绕射理论结合二阶传递函数(QTF)的方法，借助Ansys/Aqwa软件分析二阶波浪力对Spar平台动态响应的影响.王军君[9]针对深海Spar平台主体在线性波浪作用下的绕射、辐射等水动力问题进行了相关研究.

国内外学者针对Spar平台的研究主要集中在平台结构强度、系泊动力学响应和平台动态响应等方面.现有研究大多针对单平台，在可查阅到的资料中未见针对多平台的研究.平台的排布方式、系泊系统连接方式对于海上风电场的建设和安全运行具有至关重要的影响，因此笔者提出共用系泊系统多平台阵列的大型海上风电场的构想.

为研究海上风电场多平台动态响应特性，笔者建立了浮式风力机整机模型，根据势流理论对按一定方式排布的浮式风力机Spar平台进行动态响应特性分析，以期为建造海上风电场和提高其安全性提供理论参考.

1 浮式风力机整机模型

基于NREL 5 MW风力机[10]参数和OC3-Hywind Spar Buoy[11]参数建立的浮式风力机整机模型如图1所示.

图1 浮式风力机整机模型

把研究对象分为3组：单浮式风力机Spar平台、1×5线性排布的5个Spar平台和3×3排布的9个Spar平台.系泊系统采用悬链线，多台风力机之间的链接采用具有一定预张力的张力筋键，悬链线和张力筋键的详细参数设置见文献[11].

1×5(1列5台)多平台浮式风力机阵列如图2所示，平台间距为500 m.

图2 1×5浮式风力机阵列示意图

3×3(3行3列共9台)多平台浮式风力机阵列如图3所示(俯视图)，平台间距为500 m.

图3 3×3浮式风力机阵列俯视图

2 风力机空气动力学模型

浮式风力机空气动力载荷主要包括风轮和塔架所受风推力及其对风力机产生的倾覆力矩.浮式风力机推力载荷包括两部分:

(1)

式中：Fwind为推力载荷；Fblade为风轮所受风推力；Ftower为塔架所受风推力.

浮式风力机风轮气动力计算方法主要分为叶素-动量方法、二维势流方法和计算流体力学(CFD)方法三大类，叶素-动量方法简单有效，因此笔者采用叶素-动量方法计算风轮气动力.

风轮所受风推力为：

(2)

塔架所受风推力为：

(3)

风力机所受倾覆力矩为：

(4)

式中：CT为轴向推力系数；A1为风力机正常运行时风轮扫略过的面积；A2为塔架和风轮叶片在来流风方向上的正投影面积；At为塔架在来流风方向上的正投影面积；Vh(t)为海平面上塔架高度为h处的瞬时风速；ρa为空气密度；Hhub为风力机轮毂高度；t为时间.

浮式风力机正常运行时，风轮所受风推力随风速的变化如图4所示.

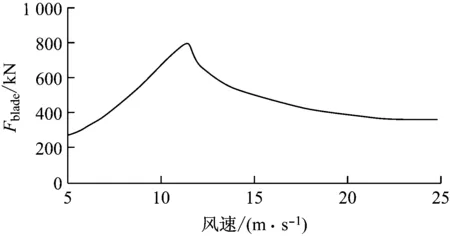
图4 风轮所受风推力

3 平台水动力学模型

浮体波浪载荷计算有2种方法：Morison方程及其修正方法和辐射/绕射理论方法.前者要求结构物对入射波场没有显著影响，不能忽略流体黏性效果.Spar平台直径为9.4 m，属于大尺度构件，结构物对入射波场有明显影响，绕射问题不能忽略，因此采用辐射/绕射理论方法.

假设流体不可压缩、无黏性、无旋运动，整个流域为浮体湿表面、波浪自由表面和海底表面构成的半无限大空间，如图5所示.图中，SD为海底表面，SF为波浪自由表面，SB为浮体湿表面，SC为无穷远处流域边界表面.

图5 波浪对物体的作用

将流场中的速度势定义为φ，包括6个自由度上的辐射波浪势、入射波浪势和绕射波浪势：

(5)

式中：φi为入射波浪势；φd为绕射波浪势；φr为辐射波浪势.

速度势φ满足拉普拉斯方程[12]、无穷远的辐射条件(Sommerfeld条件)以及其他物面边界条件：

(6)

式中：g为重力加速度，m/s2；n为浮体湿表面外法向量；vn为浮体沿外法向量n的速度，m/s；ω为波浪圆频率；θ为初相位.

根据线性化的伯努利方程，通过速度势求出一阶线性水压力梯度：

(7)

式中：ρ为海水密度.

波浪载荷作用在平台上的波浪力Fwave和波浪力矩Mwave分别为：

(8)

(9)

式中：p为压强；r为波浪力作用点到重心的距离.

4 运动方程及响应自由度

在风波联合作用下，浮式风力机平台主要为刚性运动，其运动方程为：

(10)

(11)

在外界环境载荷作用下浮式风力机平台的运动如图6所示，包括沿x轴、y轴和z轴的平动以及绕各轴的转动，平动包括纵荡、横荡和垂荡，转动包括横摇、纵摇和首摇.

图6 平台6个自由度运动

在波浪载荷作用下，平台的运动响应可由幅值响应算子ARAO来描述.ARAO是波浪波幅到平台各参数的传递函数[13]：

(12)

式中：ηi为平台运动第i个自由度的值；ξ为某一频率波浪高度的幅值.

5 计算工况

环境参数和处理步骤如下：(1) 风速为额定风速11.4 m/s；(2) 波浪谱为P-M谱，有义波高为6.5 m，波浪周期为12.23 s；(3) 风、波浪入射角均为0°(垂直入射风轮迎风面方向)；(4) 在时域计算中，仿真时间为1 800 s，时间步长为0.05 s，工况点为36 000个.

6 结果与分析

6.1计算结果可靠性验证

由于假定波浪0°入射，所以仅分析纵荡位移、垂荡位移和纵摇偏转角的响应.为验证计算结果的准确性，将模拟结果与2012年韩国海洋研究与开发协会(KORDI)的实验值[14]进行对比.平台ARAO随波浪频率的变化以及与实验值的对比见图7.

(a) 纵荡位移

(b) 垂荡位移

(c) 纵摇偏转角

由图7可知，在波浪载荷作用下纵荡、垂荡和纵摇方向上平台ARAO均随波浪频率变化，且存在峰值频率.由于Spar平台属于大尺度构件，平台固有周期较长，频率较低，易与低频波浪发生共振，所以垂荡位移和纵摇偏转角峰值频率均集中在低频波段，约为0.22 rad/s.

与KORDI的实验值对比可知，在垂荡方向上模拟值与实验值保持高度一致，纵荡、纵摇方向低频波段有轻微的差别，但总体上模拟值与实验值保持较高的吻合度.因此，在很大程度上计算结果准确可信.

6.2平台线性阵列(1×5)时域动态响应

将1×5线性阵列时各平台纵荡位移、垂荡位移和纵摇偏转角峰值与单平台对应的3个自由度峰值进行对比.

线性阵列时，各平台纵荡方向上的时历曲线如图8(a)所示.为了显示相位差别，取50 s计算时间区间.各平台纵荡位移、垂荡位移和纵摇偏转角峰值与单平台的对比如图8(b)所示.

线性阵列时，风波联合作用下各平台纵荡时历曲线以及纵荡偏转角峰值的差别均不大，但时历曲线存在明显的相位差别，主要原因是各平台在纵荡方向存在500 m的间距.

由图8(b)可知，与单平台相比，共用系泊系统有效抑制了各平台的纵荡位移响应，但是对垂荡位移、纵摇偏转角响应的影响没有明显规律.

(a) 时历曲线

(b) 峰值对比

6.3平台方阵阵列(3×3)时域动态响应

单平台与3×3阵列排布时各平台平面内位移轨迹图如图9所示.由图9可知，与单平台相比，阵列排布的平台均存在一定幅度的横荡位移，其中两侧平台(P1、P2、P3、P7、P8和P9)的运动幅度较大，约为1 m，但是比纵荡位移幅度小一个数量级.中间位置平台(P4、P5和P6)的横荡位移幅度较小，可忽略不计，主要原因是阵列中间排布的平台位于阵列的对称线位置，两侧的张紧系泊提供了大小相等、方向相反的作用力.位于两侧平台的纵荡位移小于单平台，但是中间位置平台的纵荡位移大于单平台.

6.4平台方阵阵列时域垂荡位移、纵摇偏转角统计值

纵摇偏转角响应可反映平台的倾覆程度，而垂荡位移、纵摇偏转角响应存在耦合关系，因此需要分析阵列时各个平台的垂荡位移、纵摇偏转角响应.

单平台和多平台浮式风力机时域垂荡位移、纵摇偏转角最值及其对比情况见表1和图10.由表1和图10可知，多平台方阵阵列时，顶点处4个平台(P1、P3、P7和P9)和中心位置平台(P5)的垂荡位移和纵摇偏转角响应小于单平台情况，P2、P8平台的垂荡位移、纵摇偏转角响应大于单平台情况，P4、P6平台的垂荡位移、纵摇偏转角响应与单平台较为接近.

对比P5和顶点处4个平台的垂荡位移、纵摇偏转角最值可以发现，位于中心位置的P5平台响应最值更小，原因是该平台处于中心对称位置，两侧的张紧系泊提供了方向相反的作用力，张紧系泊大大限制了平台的垂荡位移，而垂荡位移与纵摇偏转角响应是耦合的，因此P5平台响应最小.由于受到的作用力不对称，因此P2、P8平台的垂荡位移和纵摇偏转角响应要大于单平台.

表1 时域垂荡位移、纵摇偏转角最值及对比

(a) 最大值

(b) 最小值

7 结 论

(1) 浮式风力机Spar平台在纵荡位移、垂荡位移和纵摇偏转角方向的响应均集中在低频波浪阶段，约为0.22 rad/s.

(2) 1×5线性阵列排布的Spar平台纵荡位移响应均小于单平台，共用系泊系统有效抑制了平台纵荡位移响应，但是垂荡位移、纵摇偏转角响应差别不大.

(3) 3×3方阵阵列排布位于两侧的Spar平台存在较大的横荡位移，中间位置的平台横荡位移很小，可忽略不计；位于两侧的平台纵荡位移响应小于单平台，但是中间位置的平台纵荡位移响应加剧.

(4) 3×3方阵阵列排布中心位置的平台垂荡位移、纵摇偏转角响应远小于单平台，顶点处4个平台的垂荡位移、纵摇偏转角响应小于单平台，P2、P8平台的垂荡位移、纵摇偏转角响应大于单平台，P4、P6平台的垂荡位移、纵摇偏转角响应与单平台较为接近.

[1] JEON S H, CHO Y U, SEO M W, et al. Dynamic response of floating substructure of spar-type offshore wind turbine with catenary mooring cables[J].OceanEngineering, 2013, 72: 356-364.

[2] 丁勤卫, 李春, 杨阳, 等. 极限海况下三种漂浮式风力机平台的动态响应对比[J].水资源与水工程学报, 2015, 26(1): 159-165.

DING Qinwei, LI Chun, YANG Yang, et al. Comparison of dynamic response for three floating wind turbine platforms under extreme sea situation[J].JournalofWaterResources&WaterEngineering, 2015, 26(1): 159-165.

[3] 丁勤卫, 李春, 周国龙, 等. 陆海风力机动态响应对比[J].动力工程学报, 2016, 36(1): 65-73.

DING Qinwei, LI Chun, ZHOU Guolong, et al. Comparison of dynamic response between stationary and floating wind turbines[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(1): 65-73.

[4] 王颖, 杨建民, 杨晨俊. Spar平台涡激运动关键特性研究进展[J].中国海洋平台, 2008, 23(3): 1-10.

WANG Ying, YANG Jianmin, YANG Chenjun. Review on the study of Spar vortex-induced motions key characteristic[J].ChinaOffshorePlatform, 2008, 23(3): 1-10.

[5] 齐凯. Cell Spar平台概念设计及结构总体强度分析[D]. 大连: 大连理工大学, 2008.

[6] 刘毅. 单柱式浮式风机结构强度分析方法研究[D]. 上海: 上海交通大学, 2014.

[7] RAN Zhihuang. Coupled dynamic analysis of floating structures in waves and currents[D]. Texas，USA: Texas A&M University, 2000.

[8] 王东华, 叶舟, 丁勤卫, 等. 二阶波浪力作用下漂浮式风力机Spar平台的动态响应分析[J].水资源与水工程学报, 2016, 27(2): 198-204, 210.

WANG Donghua, YE Zhou, DING Qinwei, et al. Analysis of dynamic response on Spar platform of floating wind turbine under action of second order wave load[J].JournalofWaterResourcesandWaterEngineering, 2016, 27(2): 198-204, 210.

[9] 王军君. Spar平台波浪载荷计算分析[D]. 大连: 大连理工大学, 2009.

[10] JONKMAN J, MATHA D.A quantitative comparison of the responses of three floating platforms[C]//EuropeanOffshoreWind2009ConferenceandExhibition.Stockholm, Sweden: NREL, 2009.

[11] ROBERTSON A N, JONKMAN J M. Loads analysis of several offshore floating wind turbine concepts[C]//ProceedingoftheTwenty-firstInternationalOffshoreandPolarEngineeringConference.Maui, Hawaii, USA: International Society of Offshore and Polar Engineers, 2011.

[12] 唐友刚. 海洋工程结构动力学[M]. 天津: 天津大学出版社, 2008: 19-20.

[13] 李文魁, 张博, 田蔚风, 等. 一种波浪中的船舶动力定位运动建模方法研究[J].仪器仪表学报, 2007, 28(6): 1051-1054.

LI Wenkui, ZHANG Bo, TIAN Weifeng, et al. Method of ship motion modeling with dynamic positioning in waves[J].ChineseJournalofScientificInstrument, 2007, 28(6): 1051-1054.

[14] KOEDI. Concept design and analysis of floating wind turbine platforms(SHI-KORDI Joint Research)[R].Absan, Korea: Korea Ocean Research and Development Institute, 2012.

Dynamic Response of the Array of Floating Wind Turbine Platforms

DINGQinwei1,LIChun1,2,YEKehua1,HAOWenxing1,YEZhou1,2

(1. School of Energy and Power Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China; 2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China)

To investigate the dynamic response of wind turbine platform matrix, models were established based on OC3-Hywind Spar Buoy platform for NREL 5 MW wind turbine, with which, a comparison was carried out on dynamic response characteristics of floating platforms respectively in single, 1×5 linear and 3×3 square arrangement applying radiation and diffraction theory. Results show that the surge, heave and pitch response of Spar platform all appear in the range of low frequency waves; the 1×5 linearly arranged platforms have lower surge response than single platform, because the sharing mooring reduces the surge response, which does not have obvious effect on the heave and pitch response; in terms of 3×3 squarely arranged platforms, the platforms located on sides have higher swaying but smaller heave response than single platform, while the platforms in middle area have higher surging and negligible swaying response; in terms of 3×3 squarely arranged platforms, the heave and pitch response of platforms in middle area and at vertices are lower than single platform, and the response of rest platforms are not significantly suppressed.

floating wind turbine; Spar platform; array; dynamic response

2016-05-16

：2016-08-26

国家自然科学基金资助项目(E51176129)；上海市教育委员会科研创新(重点)资助项目(13ZZ120,13YZ066)；教育部高等学校博士学科点专项科研基金(博导)资助项目(20123120110008)

丁勤卫(1990-)，男，山东济宁人，博士研究生，主要从事漂浮式风力机动态响应及其优化方面的研究. 李 春(通信作者)，男，教授,博士，电话(Tel.):13301777337;E-mail:lichun128v@163.com.

1674-7607(2017)09-0744-07

：TK83

：A

：470.30