超声波检测套管井水泥环缺陷仿真模拟

解廷菊，龙士国



超声波检测套管井水泥环缺陷仿真模拟

解廷菊，龙士国

(湘潭大学材料科学与工程学院，湖南湘潭411105)

针对固井过程中由于顶替效率过低、气窜等原因造成水泥环局部缺失的现象，基于超声脉冲反射原理，运用有限元方法建立不同大小、不同方位的水泥环缺失模型，数值模拟了超声波在套管井多层介质中的传播规律。通过提取回波首波幅度、首波的接收时间，对回波进行频谱分析，对比了胶结良好和水泥环缺失两种情况下的时域特征和频域特征。在研究不同方位缺失影响时，引入了缺陷敏感频率，发现在一定激发频率下，有缺陷的位置上敏感频率会出现极大值，不同方位的缺陷有不同的敏感频率，而且区别较为显著，以此可以判断缺失方位。

超声检测；水泥环缺失；缺失方位；频谱

0 引言

在国内外的油田井建井过程中，固井是油田井建井的关键环节，也是保护油气层和保证油气井生产寿命的关键。固井质量的好坏关系到油田井勘探技术的开发效益和产能建设，具有十分重要的意义[1-2]。然而固井注水泥过程中水泥窜槽、开发过程中所采取的增产措施以及稠油热采井中出砂所造成的应力集中、注汽过程中的高温热应力等都会造成水泥环局部缺失[3]的现象。水泥环缺失情况检测变得越来越重要，引起了人们的广泛重视。国内许多研究人员在水泥胶结测井方面进行了大量理论分析和实验[4]，但是在检测水泥环缺失方面研究较少。车小花[5]等人采用物理模拟的方法研究了不同胶结状况下的声全波波形，通过分析波形判断第一界面和第二界面的胶结质量。周吟秋[6]等人讨论了套管波首播幅度关于激发声源中心频率变化的关系。许飞龙[7]等人利用超声反射法通过滤波检测水泥胶结质量，并建立有限声束模型计算了斜入射时的反射全波，探讨了入射角对反射波的影响。谢丹艳[8]等人对水平井中可能存在的水泥环上层弓形缺失，利用有限差分法实现了水平井弓形缺失复杂井孔声场的数值模拟。宋若龙[9]等人利用应力速度有限差分法并行程序对套管井扇区水泥缺失的非对称井孔声场进行研究，为反演方法提供数据，完善了分区水泥胶结测井解释方法。目前，中海油田服务有限公司研制出多功能超声成像测井仪器，采用超声脉冲反射测量技术，进行固井质量评价。

有限元法是解决诸多复杂物理问题的有效手段，ANSYS是目前世界顶端的有限元商业应用程序，是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件[10]。刘长福[11]等人使用ANSYS对超声波传播进行了仿真计算，结果能有效表现超声场的特性。基于超声脉冲反射原理，本文采用ANSYS有限元计算软件对超声波在水泥环缺陷套管井多层介质中的声场进行仿真模拟，研究了不同缺陷大小以及不同方位缺陷对超声反射回波的影响。

1 井孔声场模拟方法

1.1 有限元模型的建立

根据实际油田井结构的形貌，本文建立了两类套管井胶结良好和水泥环缺失的二维有限元物理模型。如图1所示，模型由内而外介质层依次为流体、套管、水泥层、地层，套管内半径为40 mm，各层介质参数见表1。换能器收发位置如图1(a)所示，图1(b)是水泥环缺陷模型，图1(c)是套管井30°方位水泥环缺失15°模型。其中，对水泥环缺陷模型设置了11组不同的尺寸，分别沿轴周向缺失30°～360°。选择井孔中心作为声源激发点，管壁四周作为接收点。

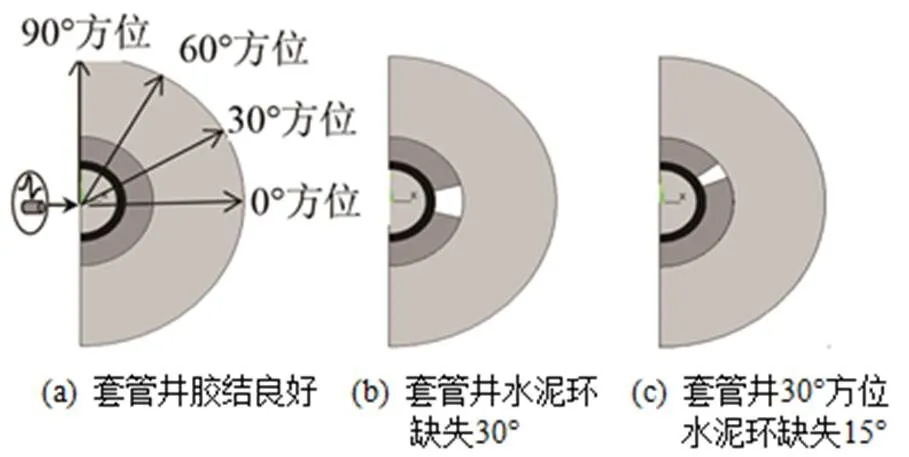
图1 有或无水泥环缺失的套管井结构物理模型

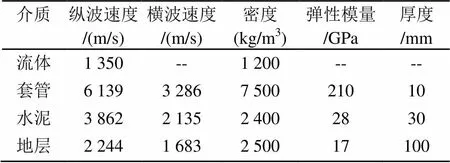
表1 模型材料参数

在确定有限元单元类型、模型材料参数后，则根据如图1中所示的简化物理模型生成相应的有限元网格划分模型。有限元模型的网格划分在有限元建模过程中极其重要，网格划分的合理性与计算结果的可靠性和准确性在很大程度上呈直接相关。如果将网格划分太粗，计算精度将会有一定的偏差，如果将网格划分太细，虽然提高了有限元模拟计算的精度，但会造成计算时间过长或占用电脑的内存过大，甚至出现电脑存储不够的问题。

为了保证计算精度，声波沿传播方向每个波长内至少有10～20个单元[12]。既要满足最大频率下波长的要求，又要综合考虑计算量。最大模型单元尺寸的选择见表2。此外，对于边界的处理，取地层厚度为管壁厚的10倍，声波到达地层后接收到的回波在150 µs左右，对前面波形的分析干扰不大，加之ANSYS某些单元的局限性不能施加吸收边界，故添加了约束。

表2 模型最大单元尺寸

1.2 声源信号的选取

本文采用的激励信号由5个单音频信号叠加并经HANNING函数调制而成，为了更好地模拟出套管井结构中的超声波传播，选择的脉冲信号频率=100 kHz，脉冲宽度=50 μs，计算时间=500 µs。这是因为超声波频率越高，其波长就越短，在传播过程中衰减就越快，尤其在缺陷模型中需要绕过缺陷传播，易产生频散现象、穿透能力差、超声波能量利用率低。而超声波频率越低，声波能量就低，在应力云图中观察不到明显的传播路径。经过多次模拟比对，选择频率为100 kHz进行模拟时接收到的波形较好，易于提取分析。声源信号的波形及频谱曲线如图2、3所示。相对于一般如半正弦信号或矩形波、尖脉冲等信号，从应力云图明显看到在传播过程中能量衰减较快，接收到的波形杂乱，不利于后处理数据提取，而HANNING窗脉冲信号主瓣高，旁瓣瞬间衰减很快，其中心频率附近集中着绝大部分频谱能量，在信号识别中频率敏感度高，这种窄带激励既可以使应力波的传播距离增大，又可以增强自身信号强度。

在本模拟过程中先编写信号函数表达式，然后以瞬时载荷的形式加载到井孔中央位置所对应的节点上(即有限元创建模型井孔中央为坐标原点，划分网格后在List/Keypoint/Coords+Attributes可查看到它所对应的节点为34)。所加载激励信号[13]的数学表达式为：

其中：为脉冲信号频率；为脉冲信号中单音频数；为时间。

图2 声源信号时域波形

Fig.2 Time domain waveform of the sound source signal

2 模拟结果分析

2.1 声波在介质中的传播声场

图4是超声波在胶结良好和水泥环缺失套管井中不同时刻传播的声场快照。由图4可见，在套管井中央加载一个声源信号，超声波就会在井孔流体中传播，由于在钢管中传播速度快，传至管壁后迅速在套管四周传播，并在水泥界面处发生反射和透射。因为存在阻抗差异，大部分能量反射回去，只有一小部分能量进入水泥环向地层传播，在水泥环与地层界面处又会反射和透射。当声波遇到缺陷时，声波会以扰动的形式绕到缺陷外侧进而在外层介质中传递能量，并在缺陷界面发生反射，如图4 (b)所示；当缺陷增大时，透射能量明显减少，缺陷两侧的反射能量增强。最后管壁四周接收到的为各个界面的多次反射波。

2.2 波形结果分析

图5是不同缺陷大小模型在0°方位上接收到的回波对比图，回波在波形上呈现几个波包。通过时域分析，在30 µs时首先接收到波形，与预期计算时间29.6 µs基本一致。48.5 µs前的第一个波包主要为套管波，即井内流体-套管界面与套管-水泥界面之间的套管内来回反射波。在水泥环缺失角度较小时，大部分能量可以通过水泥环向地层传播，套管波的波包幅度较小。当缺失角度达到180°后，水泥环的缺失造成套管内外声阻抗差异较大，能穿透套管进入地层的波能量较低，大部分能量在套管内相互反射，套管波波包的幅度随着缺失角度的继续扩大呈增加趋势，直至自由套管达到最大，即波能量只能在套管内传播，不会传递到外层介质中去。这一结果符合声波套管井水泥环缺失的基本理论，验证了该模拟的准确性。

图6为水泥胶结良好和不同水泥环缺失大小套管井在0°方位接收到的首波幅度对比图，提取其所有情况的幅度信息如图7所示(幅度进行了同比放大)。由图7可以看到，在水泥环缺失范围小于60°内，无缺陷模型首波幅度最小。但随着缺失角度的增大，首波幅度随之缓慢增大，而且从图6可观察到首波信号较完整模型出现得较晚，可能局部缺失使得信号强度较小，到180°后幅度急剧减小，并保持上下微弱波动。这是因为在缺失角度较小时，在缺陷界面处也会发生反射，这些反射叠加会使得首波幅度有一定增加。而在缺失180°之后，缺失范围较大，向外传播的能量较低，0°方位接收到的多是套管内的来回反射波，幅度自然减小。

2.3 频谱分析

快速傅里叶变换(Fast Fourier Transform，FFT)是一种快速有效的时频转换方法。通过计算，二次回波出现的时间为197.7 µs，设置采样频率为1 MHz，截取回波250个点作为采样点，对所有模型在0°、30°、60°、90°方位接收到的波形进行FFT，图8至图11分别是不同缺陷在0°方位的回波频谱曲线。

图12将所有方位FFT频谱图中的高主频值对应的振幅幅值提取出来，与缺失大小形成对应关系(幅度进行了同比放大)。频谱图中所示的幅值是由于介质界面之间的多次反射产生瞬态共振所致，对应的振幅幅值越高，表明反射次数越多，累计的反射能量越高。分析结果显示，图8无缺陷模型主频值为996 kHz，而图9缺陷模型出现单次主频左移现象，降至956 kHz，这是由缺陷使得超声波在介质中传播的高频部分衰减大引起的，而在不同方位上接收到的幅值都呈一致性变化，随着缺陷角度的增大，幅值先缓慢增大后明显增大，当缺陷角度达到180°之后乃至自由套管，幅值急剧减小，且变化趋势不明显，趋于平衡。这说明缺陷的存在使得界面之间的反射加强，幅值增大，但当缺陷增大到一定程度时，能量不会传递到外层介质，幅值会明显减小。

3 水泥环缺失方位的确定

为了分析水泥环局部缺失对声场的影响，根据声场的对称性，分别模拟了水泥环在0°、30°、60°、90°不同方位含有15°的周向缺陷，其有限元物理模型如图1(c)所示。各层介质参数和模型单元尺寸选择同表1、表2。通过对井壁四周不同方位接收到的回波进行分析，二次回波=250 µs，选取=1 MHz，分别截取无缺陷和有缺陷时的回波进行FFT，由频谱幅度谱计算缺陷对超声信号影响的敏感频率[14]，引入敏感频率主要是为了更直观得出在某缺失方位下回波FFT的不同特征，定义为

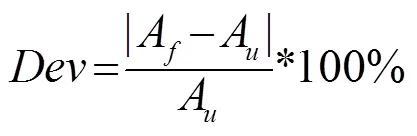
从不同方位缺陷敏感频率图13可知：0°方位缺陷在203.2、422.3、446.2 kHz有明显变化，且在446.2 kHz附近出现了极大值；30°方位缺陷在139.4 kHz附近最为敏感，同时在163.3、330.7 kHz也比较敏感；60°方位缺陷在338.6 kHz出现极大值，此频率为最敏感，此外在322.7 kHz也较为敏感；90°方位缺陷变化幅度相对平缓，幅值较低，在366.5 kHz比较敏感。当改变激励脉冲频率时，敏感频率也会发生变化，这样可以结合不同激励频率检测缺陷，对于更多外界因素如水泥层厚度、井径等，都可以通过控制单一变量来研究敏感频率的变化。

(a)0°方位

(b)30°方位

(c)60°方位

(d)90°方位

图13 不同方位上含有15°缺陷的敏感频率

Fig.13 Sensitive frequencies in different directions for defect of 15°

由以上分析可知，不同方位的缺陷有不同的敏感频率，而且区别较为显著。通过分析不同方位的敏感频率变化，结合频域信息可以为进一步判断水泥环缺失方位提供依据。

4 结论

(1) 当水泥环缺失范围小于60°内，无缺陷模型首波幅度最小，但随着缺失角度的增大，首波信号出现较晚，首波幅度随之增大，到180°后幅度急剧减小，并保持平稳。

(2) 对所有回波进行频谱分析，发现在不同方位上幅值都呈一致性变化，即随着缺陷角度的增大，幅值增大，当达到一定程度(缺陷角度≥180°)后，幅值急剧减小，变化趋势不明显。

(3) 不同方位的缺陷有不同的敏感频率，这对判断水泥环缺失方位有一定帮助。

[1] ZHANG H, XIE D, SHANG Z, et al. Simulated various characteristic waves in acoustic full waveform relating to cement bond on the secondary interface[J]. Journal of Applied Geophysics, 2011, 73(2): 139-154.

[2] 庞秉谦, 杨松, 窦益华, 等. 套管磨损与水泥环缺陷位置对套管应力的影响[J]. 石油机械, 2009, 37(10): 1-3. PANG Bingqian, YANG Song, DOU Yihua, et al. The influence of casing wear and cement ring defect position on the casing stress[J]. Journal of petroleum machinery, 2009, 37(10): 1-3.

[3] 赵鹏, 赵宝乐, 刘乐华. 水泥环缺陷对套管损坏的影响分析[J]. 油气田地面工程, 2009, 28(10): 40-41. ZHAO Peng, ZHAO Baole, LIU Lehua. Cement ring defect analysis of the influence of the casing damage[J]. Journal of Oil and Gas Field Surface Engineering, 2009, 28(10): 40-41.

[4] TANG Jun, ZHANG Chengguang, ZHANG Bixing, et al. Cement bond quality evaluation based on acoustic variable density logging[J]. Petroleum Exploration and Development Online, 2016, 43(03): 514-521.

[5] 车小花, 乔文孝, 闫向宏. 不同胶结状况对固井质量测井影响的模拟实验研究[J]. 测井技术, 2005, 29(03): 185-187. CHE Xiaohua, QIAO Wenxiao, YAN Xianghong. Simulated experimental investigation about effects of different bongdings on cement bond quality[J]. Journal of Well Logging Technology, 2005, 29(03): 185-187.

[6] 周吟秋, 王秀明, 陈德华. 套管井声波测井中首波幅度衰减研究[J]. 测井技术, 2007, 31(04): 321-326. ZHOU Yinqiu, WANG Xiuming, CHEN Dehua. First wave amplitude attenuation in cased well logging research[J]. Journal of Well Logging Technology, 2007, 31(04): 321-326.

[7] 许飞龙, 胡恒山, 尹诚刚. 通过滤波检测水泥胶结质量的超声反射法[J]. 声学学报, 2015, 40(03): 429-436. XU Feilong, HU Hengshan, YIN Chenggang. Detection of cement bond quality by filtering the ultrasonic reflection method[J]. Acta Actustica, 2015, 40(03): 429-436.

[8] 谢丹艳, 张宏兵, 孙树林. 弓形缺失水平井井孔声场数值模拟[J]. 测井技术, 2015, 39(02): 150-154. XIE Danyan, ZHANG Hongbing, SUN Shulin. Numerical simulation of borehole acoustic field in horizontal well with missing arch[J]. Journal of Well Logging Technology, 2015, 39(02): 150- 154.

[9] 宋若龙, 刘金霞, 姚桂锦, 等. 非轴对称套管井中声场的并行有限差分模拟[J]. 地球物理学报, 2010, 53(11): 2767-2775. SONG Ruolong, LIU Jinxia, YAO Guijin, et al. The parallel finite difference simulation of sound field in axisymmetric casing well[J]. Journal of Geophysics, 2010, 53(11): 2767-2775.

[10] 高兴军, 赵恒华. 大型通用有限元分析软件ANSYS简介[J]. 辽宁石油化工大学学报, 2004, 24(03): 94-98. GAO Xingjun, ZHAO Henghua. Abstract of large finite element analysis software ANSYS[J]. Journal of Liaoning University of Petroleum Chemical Industry, 2004, 24(03): 94-98.

[11] 刘长福, 牛晓光, 李中伟. 基于ANSYS的超声纵/横波传播仿真计算[J]. 无损检测, 2011, 30(06): 15-18. LIU Changfu, NIU Xiaoguang, LI Zhongwei. Ultrasonic longitudinal/transverse wave propagation based on ANSYS simulation[J]. Journal of Nondestructive Testing, 2011, 30(06): 15-18.

[12] Song K I, Cho G C. Numerical study on the evaluation of tunnel shotcrete using the impact-echo method coupled with Fourier transform and short-time Fourier transform[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(8): 1274-88.

[13] Aggelis D G, Tsimpris N, Chai H K, et al. Numerical simulation of elastic waves for visualization of defects[J]. Construction and Building Materials, 2011, 25(4): 1503-1507.

[14] 孙继华, 李书光, 倪云鹿, 等. 固体中缺陷对声波频谱特性影响的有限元仿真[J]. 计算机仿真, 2008, 25(08): 308-311. SUN Jihua, LI Shuguang, NI Yunlu, et al. Finite element simulation of the effect of defects in solid on ultrasonic spectral feature[J]. Computer Simulation, 2008, 25(08): 308-311.

Simulation of cement defect in casing well with ultrasonic

XIE Ting-ju, LONG Shi-guo

(College of Materials Science and Engineering, Xiangtan University, Xiangtan 411105,Hu’nan,China)

For studying the patial defect phenomenon of cement sheath caused by low displacement efficiency and gas channeling in the cementing process, the finite element method is used to establish different size and different orientation models of cement sheath defect and to simulate the propagation rules of ultrasound in multilayer medium of casing well. By extracting the echo amplitude and the headwave time in different directions and by analyzing ccho frequency spectrum, the time domain and frequency domain characteristics of the models are compared effectively. For determining the cement sheath defect at different orientations, the defect’s sensitive frequency (Dev) is introduced, and it is found that a great value of Dev in the defective position appears under a certain excitation frequency and the defects in different directions show different Devs, which can determine the orientation of the defect.

ultrasonic testing; cement sheath defect; defect orientation; frequency spectrum

TB553

A

1000-3630(2017)-04-0346-07

10.16300/j.cnki.1000-3630.2017.04.009

2016-08-10;

2016-10-24

湖南省教育厅重点科学研究资助项目(16A209)

解廷菊(1990－), 女, 山西朔州人, 硕士研究生, 研究方向为材料测控技术与装备。

解廷菊, E-mail: 1318346903@qq.com