一种带薄膜结构的Helmholtz腔声学超材料

2017-09-18周榕吴卫国闻轶凡

声学技术 2017年4期

周榕，吴卫国，闻轶凡

周榕，吴卫国，闻轶凡

(江苏大学土木工程与力学学院，江苏镇江212013)

为有效控制低频宽带噪声，设计了一种带薄膜结构的Helmholtz腔声学超材料。利用COMSOL软件对其透射特性进行详细分析，结果表明：不带膜的原本的Helmholtz腔结构其透射系数虽在低频范围内可以得到峰值，但其结构尺寸较大，且频带很窄，而文中设计的声学超材料结构的透射系数在低频范围可得到多个峰值，在相同结构尺寸下，与原本的Helmholtz腔结构相比，其固有频率向低频范围内偏移，因而提高了结构的低频隔声效果，拓宽了结构的隔声频率带宽。在此基础上进一步研究了声学超材料结构几何参数对透射系数的影响，优化了声学超材料的结构几何参数。

Helmholtz腔；声学超材料；透射系数

0 引言

低频噪声由于波长较长，对其有效控制一直是噪声控制领域挑战性的难题之一。在传统的低频噪声控制方法中，根据质量作用定律[1]，需要较为厚实的混凝土墙或结构较为复杂、较难制备的复合材料，而声学超材料因其具有的奇特性质(负等效质量密度和负等效弹性模量)可以有效控制低频噪声。2006年，Fang[2]等人设计了一维阵列Helmholtz声学超材料，并通过实验在kHz范围内实现了负弹性模量。2010年，Lee[3]等人采用周期排列Helmholtz共鸣器，通过实验成功验证了“双负”声学超材料。在此基础上，众多学者研究了基于Helmholtz型的声学超材料结构，王旭[4]将周期性Helmholtz共鸣器进行理论与预测对比，在宽频范围内得到了较高的传递损失。但其结构尺寸在cm级范围，无法满足小尺寸结构的应用。丁昌林[5]等人设计了一种可听声频段的声学超材料，其结构由一维Helmholtz腔周期性排列组成，但其控制频率范围高于500 Hz。随后高东宝[6]等人将Helmholtz腔单元组合成四种新型单元，研究了各单元的声透射特性，但其设计的超材料所产生的声传播禁带在kHz频率范围内。丁昌林[7]等人设计了一种开口空心球的声学超材料结构，对其结构尺寸因素、开孔方向位置和数量[8-9]、单双层[7,10-11]、空腔内填充材料[12]以及空腔与空气耦合作用[13]等方面进行了详细研究。但其研究的声学超材料透射系数最低值对应的频率均在1 000 Hz左右，且仅存在单峰。综上所述，现有的Helmholtz型声学超材料在结构尺寸优化和低频范围内的噪声控制效果仍需进一步研究。

本文设计了一种带有薄膜的Helmholtz腔的声学超材料结构，通过数值计算研究其微结构的透射性质来反映该结构在低频范围内的隔声效果，并进一步研究结构几何参数的改变对透射性质的影响。

1 模型的建立

1.1 声学超材料的模型

本文设计的声学超材料结构模型是由圆柱型的空腔结构在其上方开小圆孔，并且在中部加入薄膜组合而成，如图1(a)所示。图1(b)表示开孔圆柱空腔带膜结构的竖向剖面图，红色部分代表薄膜。图1(c)为开孔圆柱空腔带膜结构的尺寸，图1(d)～1(f)是开孔圆柱空腔的结构图、剖面图和尺寸图，用此结构与开孔圆柱空腔带膜结构作对比，研究结构加膜与不加膜对透射系数的影响。图1(g)和图1(h)分别表示两种声学超材料的排列组合。

图1 两种声学超材料结构图

1.2 透射系数的计算

开孔圆柱空腔基于Helmholtz腔共振器，其透射系数为[1]

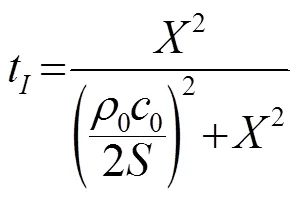
(2)

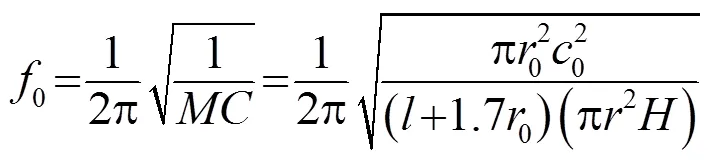
由式(3)可见，共振频率与小孔的半径、深度及空腔圆柱的半径和高度有关。

1.3 薄膜的固有频率

本文研究选取的薄膜厚度大于0.5 mm，可简化为薄圆形板来研究，其振动方程[1]为

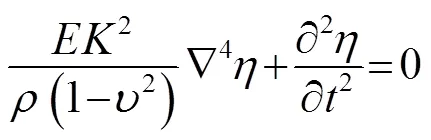
(5)

将式(5)代入式(4)，得到

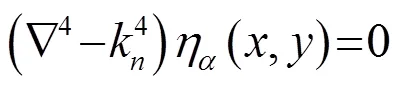
令

(7)

求解式(6)，可得

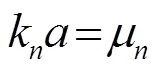
(9)

2 两种声学超材料的透射系数分析

本文分析对比了两种声学超材料的透射系数：单一的Helmholtz腔结构和带薄膜结构的Helmholtz腔。本文采用有限元软件COMSOL Multiphysics 4.3b声-固耦合模块的频率模式。单一的Helmholtz腔结构的尺寸范围为：空腔半径mm；空腔高度=20～40 mm；小孔半径mm；小孔深度～10 mm；薄膜厚度mm。元胞的材料由铝和硅胶组成，开孔圆柱空腔由铝组成，薄膜材料为硅胶，铝的材料参数为：密度=2 700 kg/m3，杨氏模量=7×1010 Pa，泊松比=0.33；硅胶的材料参数为：密度=980 kg/m3，杨氏模量=2×105 Pa，泊松比=0.49。

(a) 原本Helmholtz腔结构的透射系数

(b) 内部带膜的Helmholtz腔结构的透射系数

图2 两种声学超材料结构的透射系数

Fig.2 The transmission coefficient curves of two kinds of acoustic metamaterials

从两者的结构上看，带膜的Helmholtz腔结构比Helmholtz腔结构中间多了层硅胶膜，而上下空腔的高度与开孔圆柱空腔一致。从图2可以看出，图2(b)中和均小于图2(a)中的值。计算式(9)中硅胶薄膜的固有频率，将上述的材料参数和结构尺寸代入，可得出，152.3 Hz，和均小于。硅胶薄膜的固有频率低于空腔的固有频率，且低于值，由于硅胶薄膜和空腔发生耦合，使得低于Helmholtz腔的固有频率，而值高于硅胶薄膜固有频率和。由此可以看出，在空腔中增加薄膜可以使透射系数曲线多一个峰值，从而拓宽结构的低频带宽，并且使得结构频率向低频偏移，可以更好地用于低频噪声控制。

3 声学超材料的结构参数优化

由前面分析可知，增加薄膜可以拓宽结构的低频带宽，为了使结构达到最低透射系数频率，通过进一步改变结构参数，分析其对透射系数的影响。

3.1 Helmholtz空腔内部高度

从图3可以看出，改变空腔内部高度可以改变透射系数最低值对应频率的大小，随着空腔高度的增加，即空腔内部空气的体积增加，对应透射系数最低值的频率降低。每条曲线透射系数的最低值差别不大。与式(3)中空腔高度变化引起频率变化一致。在设计时，如若需要在低频范围内使透射系数降低，可增加空腔内部高度。

3.2 小孔的深度

保持空腔中的半径和高度以及小孔的半径不变，改变小孔的深度，取、4、6、8、10 mm。计算的透射系数曲线如图4所示。

根据式(3)，随着小孔的深度增加，透射系数最低值对应的频率降低。从图4中看，与式(3)的趋势一致，也是随着小孔的深度增加，透射系数最低值对应的频率降低。随着频率降低，带宽也随之降低。

3.3 小孔的半径

与前面一样，保持其他参数不变，改变小孔的半径，取0=0.4、0.5、0.6、0.7、0.8 mm。计算的透射系数曲线如图5所示。

从图5可知，随着小孔半径的增加，透射系数最低值对应的频率也会增加，透射系数的峰值大小随着增加。但透射系数的宽度不会改变。

由以上结构参数分析可知，要获得最低透射系数值，且最低值对应的频率较低，同时透射系数某一值的频率范围较宽，就需要增大空腔高度，选用小孔深度适宜，增大小孔半径。本文选取的空腔高度、小孔深度、小孔半径mm是最好的。

3.4 硅胶薄膜的厚度

西部受援高校学科竞争力比较分析——基于基本科学指标数据库和科研评价工具数据库………………蔡文伯杨丽雪(1·76)

带薄膜结构的Helmholtz腔声学超材料是在单一Helmhlotz腔结构的基础上加层薄膜，使薄膜上下空腔的高度保持不变，改变薄膜的厚度，取厚度、0.8、1、1.2 mm，通过有限元软件计算得出透射系数曲线如图6所示。

从图6(a)、6(c)的透射系数曲线可以看出，透射系数曲线有两个峰值，图6(c)中的两个频率低于图6(a)中的频率。从图6(b)、6(d)中可以看出，透射系数曲线有三个峰值，图6(d)中的三个频率比图6(b)中的小，并且图6(d)中透射系数的值比6(b)中的值低。由图6可知，改变薄膜的厚度会改变透射系数，取合适的薄膜厚度可得到所需频率的透射系数曲线。

(a)=0.6 mm

(b)=0.8 mm

(d)=1.2 mm

图6 不同硅胶薄膜厚度声学超材料的透射系数曲线

Fig.6 The transmission coefficient curves of the metamaterial with the thin silicone rubber membranes of different thickness

3.5 薄膜上下空腔的高度

保持薄膜厚度不变，改变薄膜上下空腔的高度即改变了上下空腔的体积。计算透射系数，其结果如图7所示。

(a)1:2=10 mm:20 mm

(b)1:2=15 mm:15 mm

(d)1:2=25 mm:5 mm

图7 不同薄膜上下空腔高度声学超材料的透射系数曲线

Fig.7 The transmission coefficient curves of the metamaterial for different heights of the cavities above and under of the thin silicone rubber membrane

结合图7(a)～7(d)的透射系数曲线可知，透射系数的峰值对应的频率和，随着上空腔高度的增加，下空腔高度的减小，值稍微增加，其透射系数峰值减小；值基本保持不变，其透射系数峰值增加。

4 声学超材料的隔声实验

为了验证理论分析结果，本文制备了声学超材料试件，如图8所示。利用北京声望阻抗管对所设计的带薄膜结构的Helmholtz型声学超材料进行隔声试验。得到的声学超材料的传递损失与频率之间的关系如图9所示。由图9可看出，频率在280 Hz 和350 Hz左右出现明显的峰值，与数值计算中的频率一致，实验与数值计算的误差是由于样品制备时的误差和放置样品时阻抗管直径的误差导致。

5 结论

本文设计了一种结构尺寸控制在mm级的带薄膜结构的Helmholtz腔声学超材料。通过COMSOL等有限单元软件计算其透射系数，结果表明，在相同尺寸条件下，带膜结构的声学超材料透射系数在500 Hz以下曲线有多个峰值，并使结构的固有频率向低频范围内偏移，拓宽了结构的低频带宽。通过优化声学超材料的结构尺寸，分析结构参数对透射系数曲线的影响，结构尺寸为、mm、mm、mm、mm时，可以得到280 Hz和350 Hz左右的透射系数值最低曲线。本文还通过隔声测试试验，研究了所设计的声学超材料结构的传声损失，试验结果与数值模拟结果一致。

[2] FANG Nicholas, XI Dongjuan, XU Jianyi, et al. Ultrasonic metamaterials with negative modulus[J]. Nature Materials, 2006, 5(6): 452-456.

[3] Sam Hyeon Lee, Choon Mahn Park, Yong Mun Seo, et al. Composite acoustic medium with simultaneously negative density and modulus[J]. Phys.Rev.Lett, 2010, 104(5): 054301-1-4.

[4] 王旭. 周期性Helmholtz共鸣器阵列理论研究[J]. 声学技术, 2013, 32(6): 235-237. WANG Xu. A theoretical study on periodic Helmholtz resonators array[J]. Technical Acoustics, 2013, 32(6): 235-237.

[5] 丁昌林, 赵晓鹏. 可听声频段的声学超材料[J]. 物理学报, 2009, 58(9): 6351-6355. DING Changlin, ZHAO Xiaopeng. Audible sound metamaterial[J]. Acta Phys. Sin., 2009, 58(9): 6351-6355.

[6] 高东宝, 曾新吾. 一维Helmholtz腔超材料声透射特性研究[J]. 声学技术, 2011, 30(6): 63-64. GAO Dongbao, ZENG Xinwu. Transmission property of 1D Helmholtz resonator metamaterial[J]. Technical Acoustics, 2011, 30(6): 63-64.

[7] 丁昌林, 赵晓鹏, 郝丽梅, 等. 一种基于开口空心球的声学超材料[J]. 物理学报, 2011, 60(04): 290-294. DING Changlin, ZHAO Xiaopeng, HAO Limei, et al. Acoustic metamaterial with split hollow spheres[J]. Acta Phys. Sin, 2011, 60(04): 290-294.

[8] DING Changlin, CHEN Huaijun, ZHAI Shilong, et al. Acoustic metamaterial based on multi-split hollow spheres[J]. Appl. Phys. A, 2013, 112(3): 533-541.

[9] HAO Limei, DING Changlin, ZHAO Xiaopeng. Design of a passive controllable negative modulus metamaterial with a split hollow sphere of multiple holes[J]. Journal of Vibration and Acoustics, 2013, 135(4): 595-606.

[10] DING Changlin, ZHAO Xiaopeng. Multi-band and broad-band acoustic metamaterial with resonant structures[J]. J. Phys. D: Appl. Phys, 2011, 44(21): 215402-1-8.

[11] CHEN Huaijun, ZENG Hongcheng, DING Changlin, et al. Double-negative acoustic metamaterial based on hollow steel tube meta-atom[J]. J. Appl. Phys, 2012, 113(10): 6351-6355.

[12] HAO Limei, DING Changlin, ZHAO Xiaopeng. Tunable acoustic metamaterial with negative modulus[J]. Appl. Phys. A, 2012, 106(4): 807-811.

[13] DING Changlin, HAO Limei, ZHAO Xiaopeng. Two-dimensional acoustic metamaterial with negative modulus[J]. J. Appl. Phys, 2010, 108(7): 074911-1-5.

An acoustic metamaterial based on Helmholtz resonator with thin membrane

ZHOU Rong, WU Wei-guo, WEN Yi-fan

(Jiangsu University,School of Civil and Mechanics Engineering, Zhenjiang 212013, Jiangsu, China)

An acoustic metamaterial based on Helmholtz resonator with inner thin membrane is designed for controlling sound wave in low frequency range. By numerical calculation and analysis, it is concluded that an original Helmholtz resonator without thin membrane needs bigger geometric sizes to get better transmission coefficient curve in low frequency range, and its frequency band is very narrow. The transmission coefficient curve of the new designed acoustic metamaterial can show more minimal values in low frequency range, so that it can get better sound insulation effect in a wider low frequency range with the same geometric sizes as the original Helmholtz resonator. In addition, the geometric sizes of the acoustic metamaterial that affect the transmission coefficient are studied and the optimal geometric sizes of acoustic metamaterial are obtained.

Helmholtz resonator; acoustic metamaterial; transmission coefficient

O422.8

1000-3630(2017)-04-0297-06

10.16300/j.cnki.1000-3630.2017.04.001

2016-09-08;

2016-11-12

周榕(1992－), 女, 江苏兴化人, 硕士研究生, 研究方向为声学超材料及噪声控制。

吴卫国, E-mail: wuwg@ujs.edu.cn