热交变载荷下10%Cr耐热钢蠕变疲劳裂纹萌生特征

，， ， ，

(1 西安石油大学 机械工程学院，西安 710065;2 博格华纳涡轮增压系统股份有限公司，德国 莱茵兰-普法尔茨州 基尔夏因博兰登 67292)

热交变载荷下10%Cr耐热钢蠕变疲劳裂纹萌生特征

崔璐1，石红梅1，张涛1，王澎2，李臻1

(1西安石油大学机械工程学院，西安710065;2博格华纳涡轮增压系统股份有限公司，德国莱茵兰-普法尔茨州基尔夏因博兰登67292)

为调节新能源间歇式发电模式所带来的弊端，需要使用火力发电厂调峰稳定电网波动。调峰过程中机组频繁启停，加剧高温部件的疲劳蠕变损伤。通过分析现有寿命模型描述温度交变载荷下汽轮机转子钢性能的不足，提出预载荷实验方案。且以预载荷实验数据为基础，优化现有寿命预测模型。通过模拟交变温度下的临近工况实验，对比应力应变关系和疲劳蠕变寿命，对所优化的寿命模型进行了评估。

热机械疲劳；10%Cr耐热钢；寿命评估；热交变载荷；预载荷；疲劳蠕变

全球节能减排的目标下，越来越多的新能源发电并网。然而这些新能源，例如光伏，风力发电等自身特点所决定的间歇式输出模式必然会给电网带来更大的波动，从而对现代化的火力发电厂提出调峰平衡电网波动的要求。调峰过程需要火力发电机组快速频繁的起停，这一过程中温度的升降所引起的交变热应力会加剧高温部件的疲劳/疲劳蠕变损伤[1]。起停过程中的平均温度通常小于机组运行温度，因此，目前对现代化火力电厂高温零部件的抗疲劳/疲劳蠕变性能研究，主要在恒定温度环境的前提条件下[2]，其中包括分析有效应力以及棘轮效应对材料性能的影响[3]。然而这种设计理念在对具有调峰要求的现代化火力发电厂高温部件寿命设计评估时，容易出现设计的过分保守而造成经济浪费，或者设计余量不够而带来不安全因素[1]。因此，温度和机械载荷同时交变工况下高温零部件的疲劳/疲劳蠕变(TMF)性能，成为当前国外研究机构和学者探索方向[1，2,4]。

疲劳蠕变载荷下的寿命预测评估，由Robinson[5]和Taira[6]提出的时间分段法(life fraction rule)已经被写入诸如ASME Code N47的标准中。这个方法是将周期性部分的疲劳损伤与直到临界疲劳蠕变寿命值的时间分段综合累积，用于寿命预测。而目前应变分段法(strain fraction rule)，即所谓延性耗竭(ductility exhaustion method)理论[7]，被工业界更广泛地使用。这个方法的难点是需要超长时间的实验来确定材料的延性耗竭能力[8]。另外一种寿命评估法是应变范围区分法(strain partitioning method)。应变范围区分法需要大量的实验来确定其所需的4种基本S-N曲线[9]。目前最常见的寿命预测方法是线性损伤累积法，此方法由于它的简单高效，常常被用于实践[2]。以上各种寿命预测方法主要用于恒温载荷条件下，很少用于起停工况交变温度和交变机械载荷同时作用工况。

本工作以现代化超超临界火力电厂发电机组启动和关闭工况为背景，分析现存的寿命模型在用于交变温度和交变机械载荷同时作用工况的不足，从理论和实验上做进一步分析。为现代化超超临界高温零部件的设计优化，运行工况优化，以及安全监控等方面提供理论依据。

1 实验材料与方案

1.1实验材料

9%～12%Cr铁素体-马氏体不锈钢具有很好的高温稳定性，常被用于现代化超超临界电厂(蒸汽温度580～600℃，压力24～35MPa)。本工作选用9%～12%Cr铁素体-马氏体不锈钢的典型代表10%Cr钢，它是由欧盟COST项目研发，主要用于汽轮机转子轴。实验材料取自于上海电气电站设备有限公司汽轮机厂最新研发的汽轮机转子，热处理工艺为1050℃/21.5h/油冷+570℃/21h/空冷+690℃/23h/炉冷，其化学成分如表1所示。

表1 10%Cr钢的化学成分(质量分数/%)Table 1 Chemical composition of 10%Cr steel(mass fraction/%)

汽轮机启停过程中，汽轮机转子轴内外温差所引起的最大热应力出现在转子表面[1]，因此本研究所用的疲劳实验试件尽可能取自转子表面，并且平行于转子轴方向。

1.2实验方案与结果

疲劳蠕变实验使用试件为标准圆柱形试样。总应变控制的实验在液压伺服式万能试验机上进行，由侧引伸计控制应变变化。

本工作的实验研究主要分为两大类：第一类是高温预载荷的模块化实验(LCF+pre-loading)，这类实验主要是为了分析热交变载荷下，交变温度与交变机械载荷二者之间交互作用对10%Cr钢力学性能的影响。实验结果是分析10%Cr钢热交变载荷下力学性能的基础，作为寿命评估模型建立的基本依据。第二类是热交变载荷下的临近工况实验(service-typeTMF)。临近工况实验是模拟发电机组的启动-运行-停机-休眠这一过程，实验结果是验证寿命评估模型的重要依据。

高温预载荷模块化实验的温度载荷谱选取超超临界发电机组典型的冷启动(300℃)、温启动(500℃)、热启动(550℃)以及运行工况(600℃)温度[1]。实验计划如图1所示。实验依据ISO12106标准执行，机械交变载荷为应变控制的三角波形。实验首先在运行工况温度T1=600℃下加载直到大约裂纹萌生寿命的一半(Ni/2)，然后在最大振幅处保载10h后逐级卸载，再降温至T2保持稳定。在温度T2下加载与温度T1下同样机械振幅的三角波直到裂纹萌生。温度T2分别选取300，500，550℃。

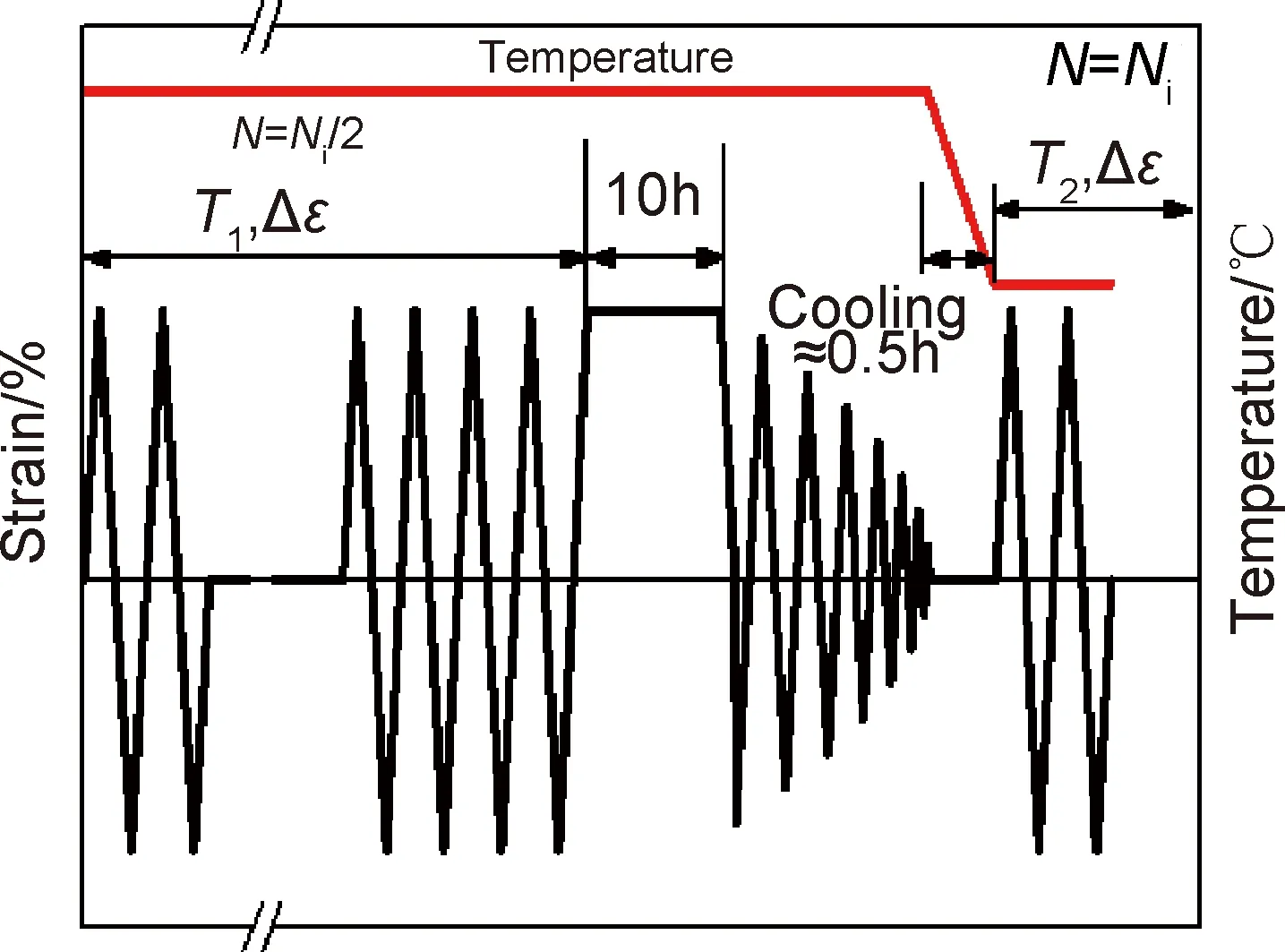
图1 预载荷实验机械载荷谱Fig.1 Mechanical load spectrum of pre-loading experiment

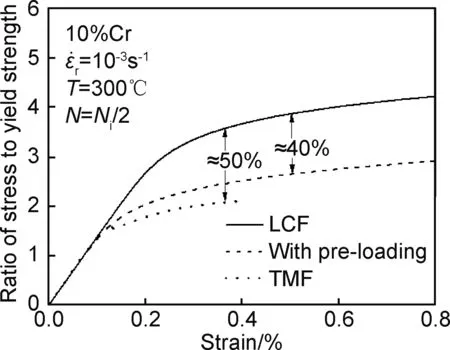
图2 一半寿命周期处300℃拉伸曲线Fig.2 Stress-strain curve by half lifetime at 300℃

图2为10%Cr钢在300℃下的拉伸曲线。经过在工况温度T1=600℃下大约一半疲劳寿命(Ni/2)的预载荷后，10%Cr钢在低温工况下的塑性区抗拉性能下降了大约40%(如图中虚线所示)，而弹性模量没有明显的变化。寿命特征关系如图3所示，图中的曲线从左向右分别为600，550，500，300℃的全寿命S-N曲线(LCF性能曲线)。空心正方形、空心三角形、空心圆形表示经过600℃一半寿命预载荷后，分别在550,500,300℃下的寿命。可以看出，经过600℃一半寿命预载荷后，其寿命比没有预载荷的寿命呈现大幅缩短，而这其中对300℃的寿命影响最大。这个规律与文献[1]中交变载荷下的寿命规律相似。

热交变载荷下的疲劳蠕变实验(TMF)的载荷谱是依据发电机组的启动-运行-停机-休眠这一过程简化得出。机组启动过程中转子轴外表面温度高于内部温度，转子表面受到由于内外温差所引起的压应变(保载阶段1)。当转子内外温度一致时，转子表面不再受到温度差所引起的应变，此时应变值为0(保载阶段2)，这一阶段也是人们常常称为的运行阶段。机组停机的时候，与启动时候的工况相似，这时转子轴表面温度低于内部，表面受到拉应变载荷(保载阶段3)。机组休眠工况，转子内外温度相同，没有应变载荷产生(保载阶段4)。

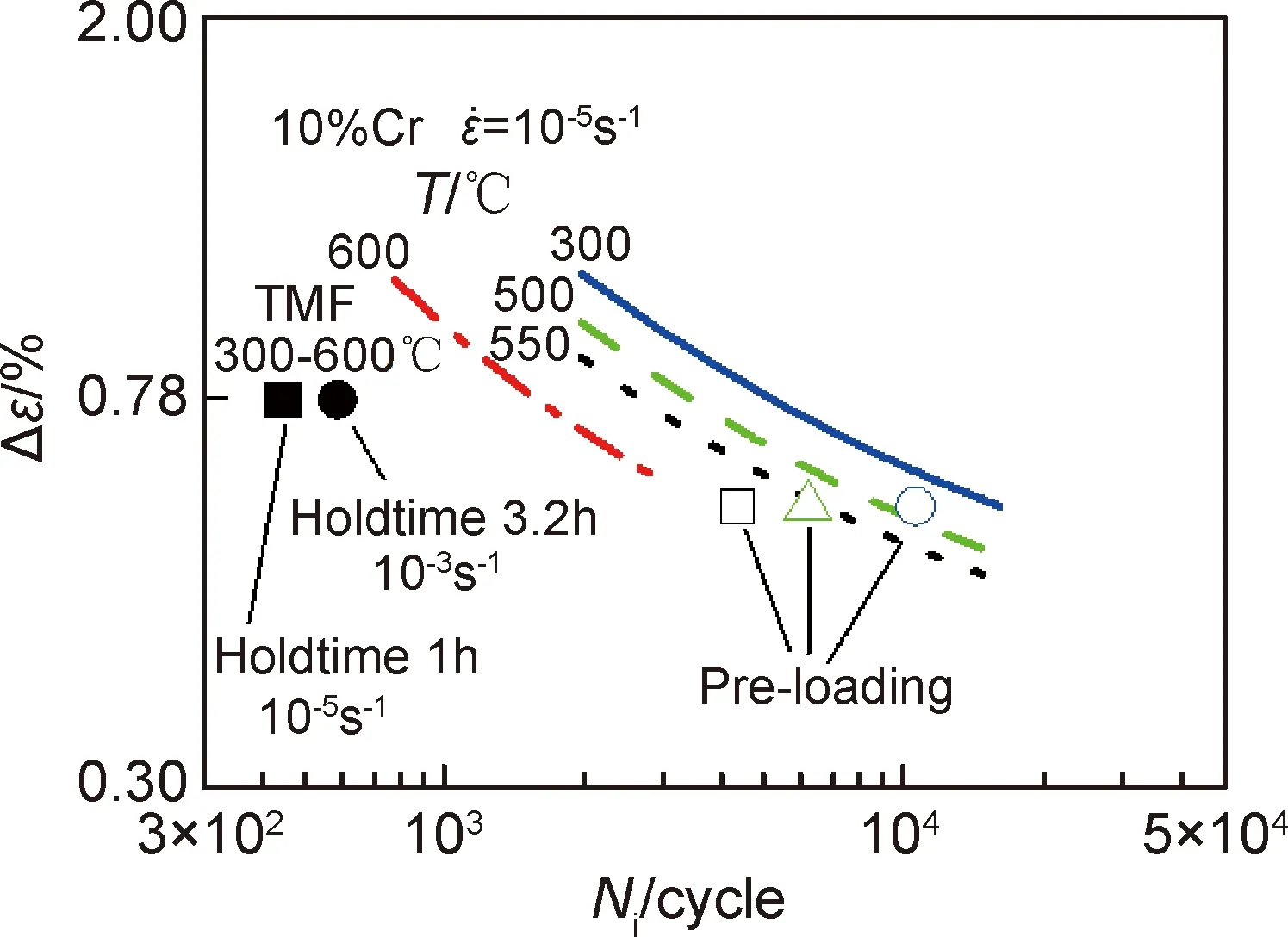
图3 10%Cr钢的S-N曲线Fig.3 S-N curves of 10%Cr steel

临近工况实验(service-type)依据标准ISO1211要求执行。温度载荷谱和应变载荷谱以及材料对这两种载荷的应力响应如图4所示[1]。温度载荷分为交变载荷(TMFloading)和恒定最高温度载荷(isothermalloading)(图4(a))。与这两种温度载荷工况相对应的应变载荷是完全一样的(图4(b))。恒温载荷下的临近工况实验是作为与交变载荷下TMF实验的对比。从图4中可以看出，TMF工况实验中，温度在最大压应变保载过程中(保载阶段1)从低温变到高温，这一应力松弛的过程中的应力松弛幅度相对于恒温状态下的应力松弛幅度要大。在最大拉应变保载过程中(保载阶段1)，温度由高温向低温变化，应力先下降后上升，而恒温载荷下应力处于连续松弛直到保载结束。

在临近工况TMF实验进行到寿命一半时，取300℃的拉伸曲线与传统LCF实验以及预载荷实验拉伸曲线对比(如图2)，可以看出，经过TMF载荷一半周期后，材料塑性区的抗拉性能比经过预载荷后塑性区的抗拉性能下降约10%，比没有预载荷(LCF)的塑形区抗拉性能下降约50%，弹性模量没有明显的变化。在图3的S-N曲线图中，实心方形表示总保载时间为1h、应变速率为10-5s-1的临近工况TMF寿命。实心圆形表示总保载时间为3.2h、应变速率为10-5s-1的TMF寿命。与S-N曲线相比，TMF的寿命幅度大幅度下降，比预载荷的寿命还要短。TMF交变载荷过程中，材料内部由于应变的累积而使内部先于表面出现裂纹，从而导致TMF寿命大幅缩短[1]。

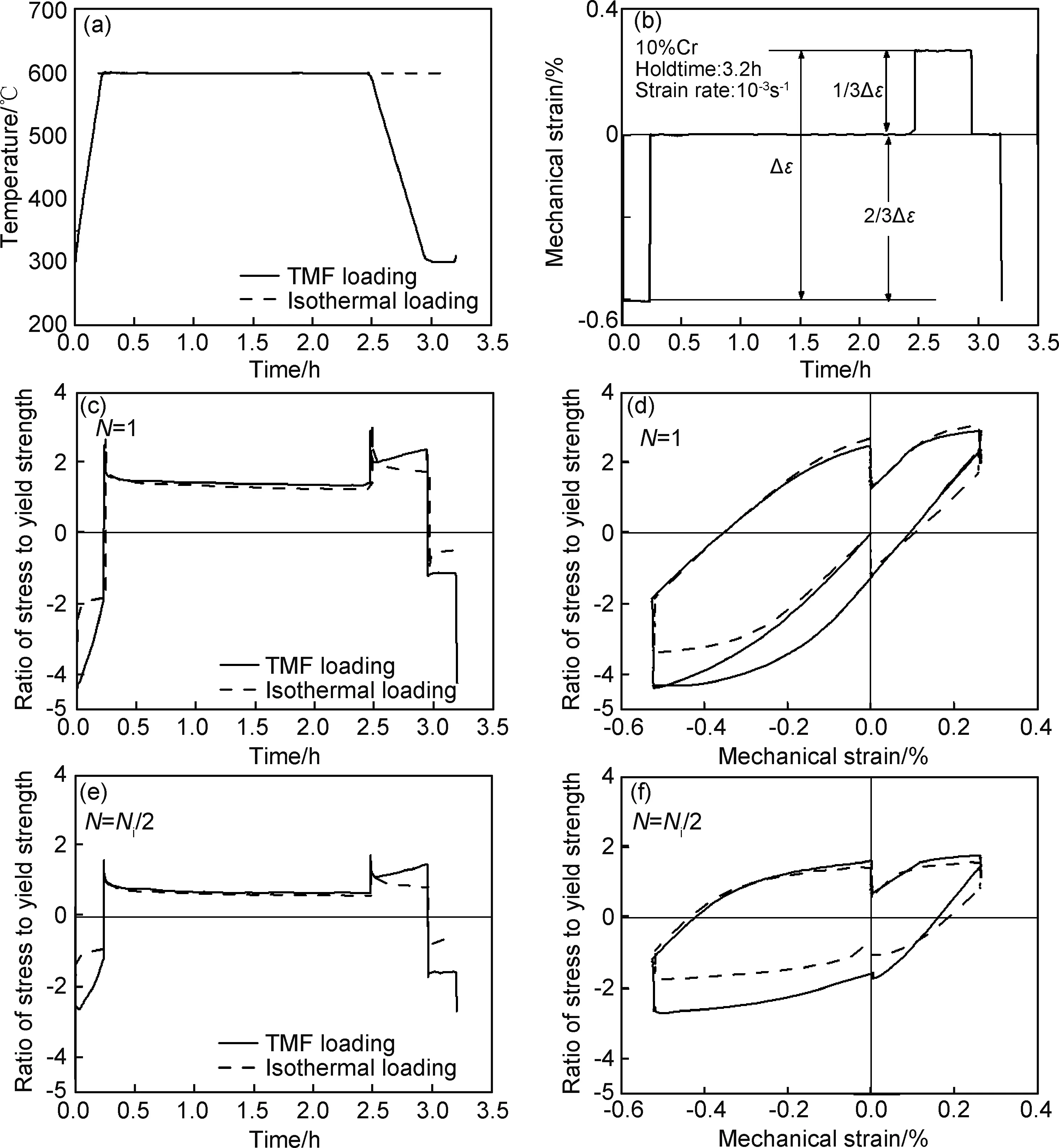
图4 临近工况实验曲线图(a)温度载荷；(b)应变载荷；(c)N=1时应力反馈；(d)N=1时应力应变关系；(e)N=Ni/2时应力反馈；(f)N=Ni/2时应力应变关系Fig.4 The curves of service-type experiment(a)temperature profile;(b)mechanical strain profile;(c)stress respond at N=1;(d)stress-strain behavior at N=1;(e)stress respond at N=Ni/2;(f)stress-strain behavior at N=Ni/2

2 寿命评估模型

寿命评估模型[10]是针对临近工况(图4)建立的唯真寿命评估模型。模型是以分析应力应变关系为基础，依据损伤累积理论，综合考虑平均应力、内应力、疲劳蠕变交互作用等因素进行寿命评估。应力应变关系主要由周期性应力屈服曲线(拉伸过程)和应力松弛曲线(保载过程)两部分组成。首先在启动温度下应力应变从零点出发到达压应变最大值，这个屈服关系曲线可以利用Ramber-Osgood方程：

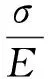
(1)

式中：σ是应力；εel和εpl分别为应变ε的弹性部分和塑性部分；E是弹性模量；K和n′分别是与温度有关的材料参数且通常由标准拉压实验(LCF)确定。周期性软化/硬化特征由参数K和n′控制，它们分别由0，5%，10%，20%，40%，60%，80%和100%寿命时的拉伸曲线确定。同理，参数K和n′分别由300℃到600℃之间6个特征温度确定，对于此范围内的任意温度值，可由两特征温度间内插法确定。

应变控制的4个保载阶段所发生的应力松弛特征可由材料的蠕变特征推出。蠕变特征可由简单的Norton-Bailey关系式：

εc=Aσntm

(2)

式中：σ是加载应力；εc为在加载应力σ下所产生的蠕变应变；参数A,m,n为与温度有关的材料参数，它们由标准蠕变实验确定。由于蠕变关系是不能直接描述应力松弛的特征，这里使用了应变强化理论(strainhardeningrule)作为辅助。对应变控制的保载阶段的描述过程中需要考虑内应力对应力松弛的影响。详细的应力应变迟滞环关系的模拟请参见文献[10]。

模型中寿命评估是以Robinson/Taira损伤累积模型为基础，综合考虑平均应力、内应力、疲劳蠕变交互作用对寿命的影响而修正。此模型由疲劳损伤Df和蠕变损伤Dc两部分组成：

D=Df+Dc

(3)

疲劳损伤Df依据Palmgren和miner理论，每个应变幅为Δε的迟滞环的所对应的损伤为1/Nio，其中Nio为该应变幅Δε所对应的疲劳寿命，由标准应变控制的拉压(LCF)实验测得。临近工况载荷下的平均应力对寿命的影响由Smith-Waston-Topper[11]参数进行修正。蠕变损伤Dc依据Robinson理论，分别对应力松弛过程中每个时间阶段的蠕变损伤进行累加，由每个真实应力等级下的时间与该应力状态下所对应的蠕变寿命的比值确定，其中真实应力涵盖了内应力载荷对蠕变寿命的影响。每个保载的开始阶段是应力松弛下降最快的一段时间，这段时间内的微观损伤形貌又因应变幅的从大到小分为穿晶、混合、延晶损伤形貌。这段时间依据损伤形貌的特征综合考虑疲劳蠕变交互作用，文献[2]给出了详细的数学描述法。疲劳损伤Df和蠕变损伤Dc循环累积直到达到所给定的临界损伤值Dcrit。10%Cr钢的临界损伤值Dcrit为0.68[12]。

3 热交变载荷下裂纹萌生特征模拟与讨论

寿命模型的可靠性评估是利用模拟临近工况热交变载荷下实验来实现的。评估分为应力-应变关系模拟和寿命预测模拟两部分。

利用上述模型对临近工况下应力-应变关系的模拟结果如图5所示。图中曲线表示计算模拟结果，图形代表实验测量的结果。图5(a), (b)分别表示恒温工况下的第一个迟滞环(N=1)和寿命一半时的迟滞环(N=Ni/2)，图5(c), (d)分别表示TMF载荷下的第一个迟滞环(N=1)和寿命一半时的迟滞环(N=Ni/2)。可以看出，模型可以比较好地重现出实验测量结果，尤其是在对最大压应变过程中应力随温度的升高而增大的描述，以及在最大拉应变过程中应力随温度的降低先下降后上升特征的描述。这也说明这两个保载变温过程中，应力变化一方面由蠕变特征影响，另一方面由随温度变化的弹性模量影响，并且弹性模量的影响起主导作用。在交变温度工况下，模型对一半寿命周期时的迟滞环下半部分的塑性性能描述得略微欠缺，这与模型中控制拉伸曲线性能的参数有关。模型中描述拉伸性能的参数是由标准拉压实验(LCF)确定，而LCF实验没有考虑材料受到高温预载荷(损伤)时的形变特征。温度交变的临近工况实验(TMF)，材料在高温区(600℃)所产生的损伤使得低温区(300℃)的塑形抗拉性能大幅度缩小(循环软化程度大幅度增加)。为了在TMF工况下综合考虑交变温度所带来的损伤交互影响，将使用预载荷实验数据替代标准拉压实验(LCF)数据用于模型材料参数的优化，优化后的模型与上述模型的模拟结果和实验结果的对比如图6所示。模拟结果显示，模型通过预载荷实验数据优化后，能够更加准确地描述塑性区的抗拉性能趋势。图6中优化后的模拟曲线相对实验结果整体向上有一定的偏移，这是由于最大拉应变保载过程的应力松弛所引起，下一步的优化方向将考虑对变温保载过程应力松弛性能的描述。

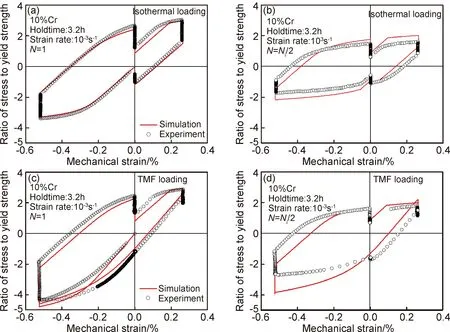
图5 模拟和实验得到的临近工况下的应力-应变曲线(a)恒温载荷工况，N=1;(b)恒温载荷工况，N=Ni/2;(c)TMF载荷工况，N=1;(d)TMF载荷工况，N=Ni/2Fig.5 Comparison of hysteresis loops at isothermal and TMF loading result of finite element analysis (a)isothermal loading，N=1;(b)isothermal loading，N=Ni/2;(c)TMF loading，N=1;(d)TMF loading，N=Ni/2

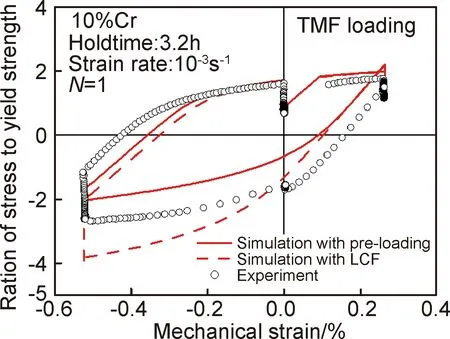
图6 优化模型与原模型和实验得到的热交变载荷下的应力-应变曲线Fig.6 Comparison of hysteresis loops at TMF loading result of two different finite element analysis and experiment

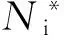
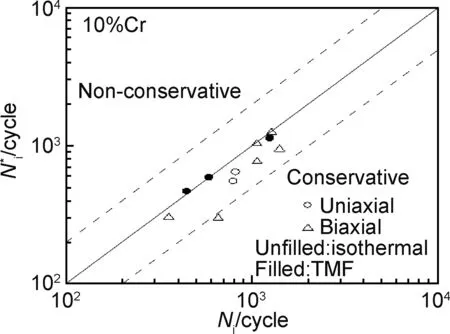
图7 优化模型的预测寿命与实验结果的对比Fig.7 Comparison of the life time estimated by optimization mode and experiment

4 结论

(1)模块化预载荷实验分析得出，10%Cr钢经过高温预载荷后，会使它在低温区的塑性抗拉性能大幅度缩小。

(2)以标准拉压实验(LCF)为基础参数的现有寿命评估模型，不能很好地描述热交变载荷工况下10%Cr钢的性能。

(3)以高温预载荷实验数据为基础所优化的寿命评估模型，可以很好地描述热交变载荷下的应力-应变关系，并且所预测的寿命更加符合实验测量的结果。

[1] CUI L,WANG P, HOCHE H, et al. The influence of temperature transients on the lifetime of modern high-chromium rotor steel under service-type loading [J]. Mat Sci Eng A,2013, 560：767-780.

[2] SCHOLZ A, BERGER C. Deformation and life assessment of high temperature materials under creep fatigue loading[J]. Materialwissenschaft und Werkstofftechnik,2005, 36(11):722-730.

[3] ZHAO P, XUAN F. Ratcheting behavior of advanced 9%-12% chromium ferrite steel under creep-fatigue loadings[J]. Mechanics of Materials, 2011, 43: 299-312.

[4] MAZZA E, HOLDSWORTH S R, SKELTON R P. The response of 1CrMoV rotor steel to service-cycle thermomechanical fatigue testing[J]. J Test Eval,2004, 32(4): 255-261.

[5] ROBINSON E. Effect of temperature variation on the long-time rupture strength of steels [J]. Trans ASME, 1952,74(5):777-780.

[6] TARIA S. Lifetime of structures subjected to varying load and temperature [M]// Creep in Structures. New York: Academic Press,1960: 96-124.

[7] PRIEST R, ELLISON E. A combined deformation map ductility exhaustion approach to creep-fatigue analysis [J]. Mater Sci Eng,1981, 49:7-17.

[8] HOLDSWORTH S R. The ECCC approach to creep data assessment [J]. ASME J Press Vessel Technol,2008，130(5)：1-6.

[9] MANSON S S, HALFORD G R. Relation of cyclic loading pattern to microstructural fracture in creep-fatigue [C]// Birmingham, England: Proc of Fatigue 1984, 2nd Int Conf on Fatigue and Fatigue Thresholds, 1984: 1237-1255.

[10] CUI L, WANG P. Two lifetime estimation models for steam turbine components under thermomechanical creep-fatigue loading [J]. Int J Fatigue, 2014, 59 :129-136.

[11] SMITH K N, WATSON P, TOPPER T H. A stress-strain function for the fatigue of metals [J]. J Mater,1970,5(4):767-778.

[12] HAASE H. Betriebsähnliches langzeitdehnwechselverhalten modernermartensitischer 9 bis 10%-Cr-stähle [D].Darmstadt: Technische Universität Darmstadt, 2004.

(本文责编：解 宏)

CreepFatigueCrackInitiationBehaviorof10%CrHeatResistantSteelUnderThermomechanicalLoading

CUILu1,SHIHong-mei1,ZHANGTao1,WANGPeng2,LIZhen1

(1SchoolofMechanicalEngineering,Xi’anShiyouUniversity,Xi’an710065,China;2BorgWarnerTurboSystemsGmbH,Kirchheimbolanden67292,Rhineland-Palatinate,Germany)

To adjust the oscillation of renewable energy sources in the discontinuous generation of electricity, power plants will be used to stabilize the fluctuations. Fatigue creep damage on power plant components will be increased, during the frequent start-up and shut-down processes of the units. A pre-loading experiment plan was introduced through the analysis on the insufficient stress-strain behavior of gas turbine rotor under thermomechanical loading described by an existed lifetime estimation model. Based on the data of the pre-loading experiments, the current life prediction model was optimized. By comparison of the simulated stress-strain behavior and estimated fatigue creep life near working condition test at alternating temperatures, the optimized life prediction model was evaluated.

thermomechanical fatigue;10%Cr resistant steel;lifetime estimation;thermomechanical loading;pre-loading;fatigue creep

10.11868/j.issn.1001-4381.2015.001208

TB301

： A

： 1001-4381(2017)09-0143-06

国家自然科学基金(51305348);德国AVIF基金项目(A232)；陕西省青年科技新星项目(2015KJXX-37)

2015-10-02;

：2017-04-20

崔璐(1979-)，女，副教授，博士，从事特殊环境下机械设备环境疲劳理论与工程应用研究，联系地址：陕西省西安市电子二路18号西安石油大学机械工程学院(710065)，E-mail:cuiluxa@hotmail.com