创设各类问题情境，组织学生自主探究——“基本不等式”教学案例

江苏省南京市临江高级中学 李仲胜

创设各类问题情境，组织学生自主探究
——“基本不等式”教学案例

江苏省南京市临江高级中学 李仲胜

当代教育家苏霍姆林斯基指出：“在人的心灵深处，都有一种根深蒂固的需求，这就是希望感到自己是一个发现者、研究者，而在人的精神世界中，这种需要特别强烈。”因此，在课堂教学过程中，教师应充分发挥学生的主观能动性，设计探索性与开放性的问题，给学生提供自主探索的机会，使他们积极主动地参与学习的全过程。课堂教学关键是“问题情境”的设置，通过“问题情境”的创设，使学生产生认知冲突，激发学生探究知识的欲望。本文中，笔者结合高中数学《必修5》中“基本不等式”这一节内容的教学，谈谈在课堂教学中如何以问题为中心组织学生自主探究。

一、创设应用性问题情境，开展探究性活动

在讲授“基本不等式”这节课时，如果按照教材内容直接给出定理，学生会觉得很枯燥。我在教学中精心设计了如下问题：

问题1：我们教室前面的花坛是边长为13米的正方形（如图1）。现想种植四种不同颜色的花，请问：能不能设计出面积相等且长和宽分别为6米和7米的小长方形方块？如果能，设计出图案（如图2）。若把正方形的边长改为（a+b）米，小长方形的长和宽分别为a米和b米，情况又会怎么样呢？

问题2：求正数a 和b的等差中项和等比中项，并猜想它们的大小关系。能不能根据问题1来验证？

问题1的提出使学生产生了兴趣，同学之间马上议论起来。他们觉得问题有趣、亲切，于是大家都跃跃欲试设计图案。经过分析，动手操作，互相交流，互相探讨，最后设计出如下美丽图案（如图3、图4、图5），有些同学还涂上了各种颜色。

从设计的图形中可直观得出：S正方形≥4S小长方形（当a=b时，取等号），即：，对于问题（2），要求正数a和b的等差中项和等比中项，同学们认为太容易了，但要比较它们的大小时，同学就有点疑惑了，难以确定。老师给足时间，让学生仔细猜想，认真讨论，并在关键时引导他们用特殊值来思考或观察问题（1）的结果，找出问题之间的关系。于是同学们都积极参与，经过思索、比较、验证，终于猜想出（a＞0，b＞0），这样学生在愉快、有趣的活动中不知不觉探究到了数学定理，这时再给出基本不等式的定理已是水到渠成了。

二、创设开放性问题情境，开展探究性活动

证法1：用不等式基本性质：由（a-b）2≥0 得：（a+b）2-4ab≥0，∵a＞0，b＞0，（当且仅当a=b时，取等号）。

显然，④是成立的。当且仅当a=b时，④中的等号成立。

证法3：用问题（1）中的正方形面积大于或等于四个长方形面积之和，得：（a+b）2≥4ab，从而可得：

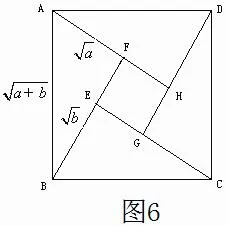
通过创设开放性问题3并进行一题多解，可使学生拓宽视野，并从几何图形中（如图6）直观认识基本不等式定理，深刻理解基本不等式定理的意义，尤其能通过图形理解定理中的等号条件。在课堂上多提出一些开放性问题，多开展这样的探究性活动，既能使学生理解和掌握课本的知识，又能达到培养学生学习兴趣和创新能力的目的。

三、创设变换引申问题情境，开展探究性活动

在课堂例题的教学中，如果就题讲题，不思变换，学生往往印象不深，只知其一，不知其二，不能理解其中奥妙，若能通过一些让学生感到意外的变例加以刺激，使他们无意之中看到了问题的严重性，往往可以引起学生的极大兴趣和高度注意，从而留下较为深刻的印象。

以上几个方面的变化有一定程度的关系，但不尽相同。给学生以神秘感，教师正好利用这点来集中学生的注意力。通过例题讲解和引申问题的探究，使学生真正理解和掌握基本不等式定理的“一正、二定、三相等”，并且知道怎样利用基本不等式定理求最值，问题4、5看似简单、容易，但设有陷阱，能使粗心大意、考虑不周全的学生受到挫折。同时，问题难度是递进式的、有层次的、由浅入深、由易到难的，这样能使学生紧紧围绕问题，逐步深入开展探究，从而使学生的探究能力得到提高，得到升华。

四、创设质疑性问题情境，开展探究性活动

在课堂练习中制造明显错误，通过就错论错，错中见正，不仅能有效地帮助学生辨别是非，解决疑惑，走出困境，更能激发学生的学习热情与求知欲，积极思考，踊跃发言，令课堂气氛活跃，课堂教学的效果也就更好了。看下面例题：

∴所以x+y的最小值为9 。

出示问题6后，学生个个睁大眼睛，上下来回看了一遍又一遍，如此答案，在学生看来似是而非，但错在何处却又迷惑不解，课堂气氛随即活跃起来。大家都觉得两种解法都对，但又不知道答案为什么会不一样，不能辩明事理。教师若一语道破了玄机，则不仅会使课堂教学失去生机，更重要的是难以达到预期效果。教师不着急，让学生自由探究，终于有一双慧眼发现了问题（6）的甲方法中，两次用到基本不等式定理时，等号成立的条件不一致，故甲方法是错的。通过对问题6的探究，使学生更全面、更深刻地理解定理，同时也提升了学生的学习热情。

五、创设趣味性问题情境，开展探究性活动

在课堂上或课后，老师可适当对定理、例题等知识进行引申推广，创设趣味性问题，提高学生的学习兴趣与热情，提高学生的求知欲，使学生在思考与探索问题的过程中掌握知识。

我在这节课的课外练习中补充了下面的问题：

问题7：

观察上述各小题的结论，探究其规律，你们能得出什么结论？

让同学们经过观察、思考与探索，自己得出结论：“若干个正数的算术平均数大于或等于它们的几何平均数。”

总之，通过对定理、例题等知识的引申推广，创设一些趣味性问题让同学们思考与探索，有助于培养学生观察、类比等解题的能力，提高数学思维，有助于培养学生的学习兴趣和探索精神，让同学们通过自己的努力得出一些性质、公式，可让他们有一定的成就感，使他们的学习兴趣更浓，学习热情更高涨。

由此可见，在数学课堂教学中，教师要精心设计有针对性、启发性和趣味性的问题，为学生创设探究性活动的氛围，从而使学生的学习达到最佳效果。在中学数学教学中开展探究性活动，有利于培养学生的数学情感，增强学生学好数学的自信心和克服困难的意志，有利于加深学生对所学知识的理解，掌握解决问题的方法和策略，更有利于培养学生的自主学习意识和合作精神。