基于改进履带式车辆微动模型的雷达微多普勒效应
2017-09-16贠乐应
贠乐应, 吕 军, 李 彤, 汪 熙, 刘 磊
(1. 装甲兵工程学院信息工程系, 北京 100072; 2. 63752部队, 陕西 渭南 714000)
基于改进履带式车辆微动模型的雷达微多普勒效应
贠乐应1, 吕 军1, 李 彤1, 汪 熙1, 刘 磊2
(1. 装甲兵工程学院信息工程系, 北京100072;2.63752部队, 陕西 渭南714000)
针对现有履带式车辆微动模型未考虑履带具体构造、雷达与车辆空间位置关系及履带裙板遮挡效应等问题,在分析履带式车辆结构、运动特性及雷达工作原理的基础上,提出了一种改进的微动模型,与现有模型相比,该模型对微多普勒频率的刻画更加精细。通过仿真得到车体平动和履带、负重轮等微动产生的雷达回波观测信号,使用短时傅里叶变换、Wigner-Ville分布、伪Wigner-Ville分布、平滑伪Wigner-Ville分布、自适应最优核时频分布、重排平滑伪Wigner-Ville分布等6种方法对仿真信号进行时频分析,比较其多普勒及微多普勒效应,从时频分辨率和交叉项2个方面比较不同时频分析方法在分析履带式车辆微多普勒信号时的性能优劣。最后,进行实测数据试验,通过与传统及改进模型仿真结果对比,验证了改进模型的正确性和微多普勒效应的实际可观测性。
履带式车辆; 微动模型; 微多普勒效应; 时频分析; 雷达回波
装甲车辆是地面战场的主要武器装备,也是车载雷达目标识别的重点对象,但因不同装甲目标的形状、体积和表面材质等非常相似,给识别带来了很大困难,而微动概念的提出为刻画装甲目标精细结构提供了新的思路[1]。微动和微多普勒概念最早由美国CHEN博士于2000年从激光领域引入雷达研究领域[1]。装甲目标的微多普勒是其微运动部件产生的多普勒调制,能够反映装甲目标的独特性质,所以可以通过提取其雷达回波的微多普勒特征进行目标识别。
不同目标具有不同的微动零部件,可根据其微多普勒信号的差异来初步判定目标的类别。但由于各类目标微多普勒效应的具体表现形式是未知的,因此在分析目标的实际雷达回波之前,需要对目标进行微动建模研究,理论推导出目标不同零部件的微多普勒信号的具体表现形式,并与实际回波信号进行对照分析,只有二者变化规律一致,才能说明实际回波中微多普勒效应的存在性、可观测性及理论建模的正确性。
目前关于装甲目标微动模型的研究中,大都把车轮、履带从车辆整体中分离出来进行简化,没有考虑履带的具体构造、车辆与雷达相对位置变化的影响及部分装甲目标履带裙板的遮挡效应[2-3],所以有待进行更贴近实装的模型分析。基于此问题,笔者对履带式装甲车辆的微多普勒效应展开研究,通过分析其结构、运动特性及电磁散射效应,建立改进的微动数学模型,对所得的仿真信号进行时频变换,分析其微多普勒效应,并通过与改进及传统模型仿真结果时频图的对比,验证了改进模型的正确性以及微多普勒效应的实际可观测性。
1 改进的履带式车辆运动模型
本文以某型坦克为例进行分析,建立其运动模型,如图1所示。与传统的履带式车辆微动模型相比,本文所提的改进模型加入了雷达与履带式车辆的相对位置关系分析、履带裙板的遮挡效应分析以及负重轮的微动分析等。
图1中:(U,V,W)为雷达坐标系,雷达静止于其坐标原点Q处;(X,Y,Z)为参考坐标系,随车辆一起运动,Q1点是参考坐标系的坐标原点,位于后侧主动轮轮心位置处,参考坐标系与雷达坐标系始终保持平行关系;目标坐标系(x,y,z)的坐标原点也是Q1点,与参考坐标系的原点重合,其3个坐标轴分别始终与车辆长、宽、高3个方向平行。
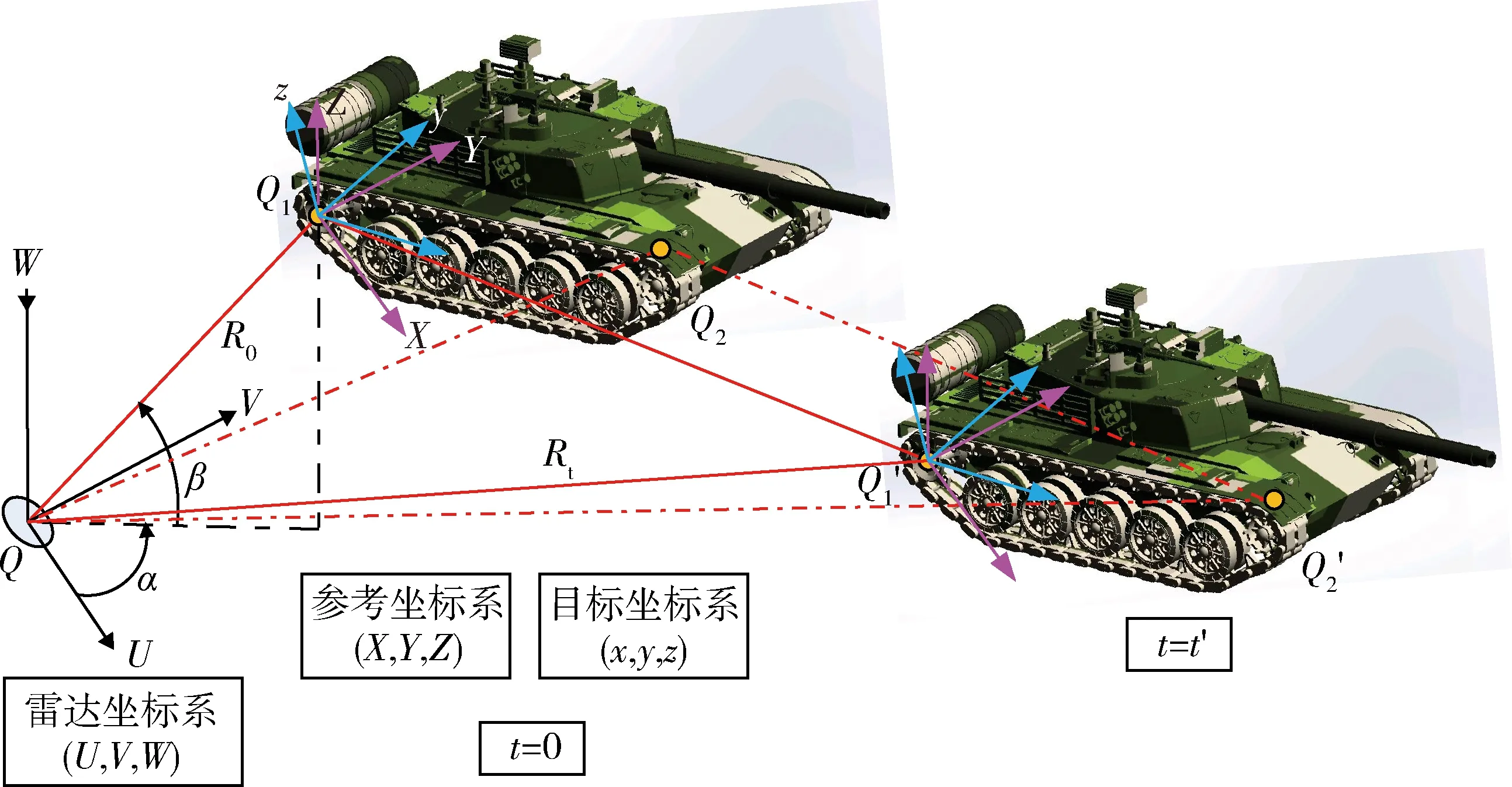
图1 改进的履带式车辆运动几何模型
假设t=0时刻,Q1点在雷达坐标系中的初始位置是R0=(U0,V0,W0)T,初始的方位角和俯仰角分别为α和β,此时雷达视线(LightofSight,LOS)的方向向量为[1]

(1)
车辆在参考坐标系中运动初速度和加速度分别为v0和a,其方位角和俯仰角分别为θ和φ,则x轴(车辆前进方向)在雷达视线方向的方向向量为
n2=(cosφcosθ,cosφsinθ,sinφ)T,
(2)
y轴在雷达视线方向的方向向量为
n3=(-sinθ,cosθ,0)T,
(3)
z轴在雷达视线方向的方向向量为
n4=(-sinφcosθ,-sinφsinθ,cosφ)T。
(4)
目前大多数装甲侦察车的车载雷达都工作在X波段,发射的电磁波为厘米波,波长远小于履带式车辆,故满足散射点模型,即目标是离散点散射体的集合,从目标返回的后向散射信号可以近似地认为是目标上一组散射中心反射出来的[4]1-2。
1.1车辆平动模型及其多普勒效应
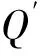
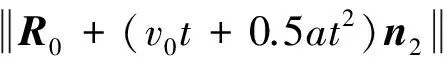
(5)

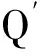

(6)
则这2个散射点的雷达回波可表示为[1]
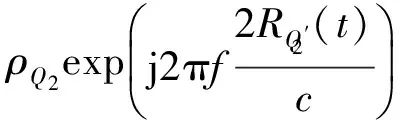
(7)
式中:ρ为目标点的反射率;f为雷达发射波的载频;c为电磁波的传播速度。
对相位项关于时间求导可推导出主体散射点Q1的多普勒频率fQ1为[4]26-27

(8)


(9)
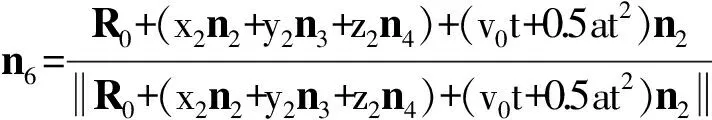
由此可得如下结论:1)车体不同部位平动产生的多普勒频率近似一致,故可将车身平动简化为一个平动散射点的运动;2)车辆沿一个方向做匀加速直线运动时,其多普勒频率呈线性变化,变化率与加速度成正比。
1.2履带微动模型及其微多普勒效应
履带的转动是履带式车辆的主要微动形式,传统的履带模型如图2(a)所示,将整个履带视为一条无缝隙的链条进行微多普勒分析,但事实上相邻履带板之间用履带销连接时有与主动轮啮合的间隙,同时雷达视线方向与履带运动方向一致,未考虑其空间位置关系。本文提出的改进履带模型如图2(b)所示,将每个履带板的外侧几何中心视为散射中心,此时雷达信号为有限个散射点回波信号的和,而非传统模型中整个履带长度方向上的积分。当坦克有履带裙板遮挡时,其模型如图2(c)所示,其微多普勒效应由未遮挡部分履带板产生。同时,在车辆整体上加入空间位置关系,即车辆行进方向在雷达坐标系的方位角和俯仰角。

图2 履带运动几何模型示意图
在1.1节分析的基础上,目标坐标系的原点仍为Q1点,履带可根据运动形式分为6段,其中:AF、CD段平行于x轴,长度分别为lAF和lCD;BC、DE段与x轴的夹角分别为π-ε和ε,其长度均为lBC,AB、EF段为圆心角为3π/4的圆弧,半径为R。
当t=0时,假设AB段一履带板中心点为P0,P0Q1与AQ1的夹角为ψ1,经过时间t1,t2,…,t6,P0点分别运动到AB段中的P1点,AF段中的P2点,EF段中的P3点,DE段中的P4点,CD段中的P5点和BC段中的P6点。
则当0 (10) 当ψ1R (11) 当ψ1R+lAF (12) 当ψ1R+lAF+0.75πR [(s4-lAF-ψ1R-0.75πR)sinε+ Rsin(0.25π)]n4+[lAF+Rcos(0.25π)- (13) 当ψ1R + lAF+0.75πR + lBC Rsin(0.25π)]n4+[lAF- (s5-lAF-ψ1R-0.75πR-lBC)- (14) 当ψ1R+lAF+0.75πR+lBC+lCD (s6-lAF-ψ1R-0.75πR-lBC- (15) 同理,履带式车辆微动散射点P处的雷达回波可表示为 (16) 则在t1时刻微动散射点P1的微多普勒频率fP1为 cos(ψ1-φ1)n2T]n7; (17) 在t2时刻微动散射点P2的微多普勒频率fP2为 (18) 在t3时刻微动散射点P3的微多普勒频率fP3为 (19) 在t4时刻微动散射点P4的微多普勒频率fP4为 (20) 在t5时刻微动散射点P5的微多普勒频率fP5为 fP5=0; (21) 在t6时刻微动散射点P6的多普勒频率fP6为 (22) 式(17)-(22)中:n7、n8、n9、n10、n11分别为QP1、QP2、QP3、QP4、QP6的方向向量,同1.1节分析可知当目标位于雷达远场时,n7≈n8≈n9≈n10≈n11≈n1。 由此可得如下结论: 1)履带微动产生的微多普勒频率与车辆初速度、加速度、车辆位置、车辆行进方向及履带位置相关;2)车辆沿一个方向做匀加速直线运动时,不同履带板微动产生的微多普勒频率的变化趋势相同,即履带AF、BC、DE段的微多普勒频率呈线性变化,AB、EF段的呈类正弦形式变化,CD段相对雷达无径向速度,故不产生微动信号;3)有履带裙板遮挡时,微多普勒频率主要由BC、DE段处的履带板产生,其微多普勒频率呈间断的线性变化趋势。 1.3负重轮转动模型及其微多普勒效应 当履带式车辆挂有履带裙板时,大部分履带被遮挡,但对负重轮的遮挡不太明显,此时负重轮的转动成了主要的微动形式,因此与传统的模型中只分析履带微动相比,本文在改进模型中加入了负重轮的微动分析。同时与传统车轮模型在车轮圆周上积分相比,本文提出的改进模型视车轮每根轮辐为一个散射中心,以此进行微动建模。 在1.1节分析的基础上,假设在t=0时履带式车辆负重轮轮心为K,半径为r,轮心在目标坐标系中的位置为(x3,y3,z3),负重轮上某辐条上转动的散射中心为点J,JK与z轴的夹角为ψ2(初始旋转角[1]),到达时间t时该点运动到J′处,转过角度φ2,φ2=ω2t,其中ω2为负重轮旋转角速度,则负重轮转动示意图如图3所示。 图3 改进的负重轮运动几何模型示意图 则t时刻,J′点到Q点的距离为 (23) 散射点J′的微多普勒频率为 (24) 式中:n12为QJ′的方向向量,n12≈n1。 由此可得如下结论: 1)负重轮微动产生的微多普勒频率随时间呈类正弦形式变化,不仅与车身在雷达视线方向的速度分量相关,还与负重轮轮辐的初始旋转角相关,轮上有n个辐条时,存在n个具有不同旋转角的散射中心,因此会产生n个t=0时刻频率不同但具有相同变化规律的微多普勒频率,变化周期与负重轮的转速相关;2) 与1.1节中车身不同位置处产生的多普勒频率近似相同一样,多个负重轮产生的微多普勒频率也近似一致,故可认为负重轮的个数不影响微多普勒频率的大小。 由上节知微多普勒频率通常随时间呈非线性变化,利用传统的傅里叶变换无法很好地描述其变化规律,需要用到联合时频分析[4]99。 现有的时频分析方法主要有短时傅里叶变换(Short Time Fourier Transform, STFT)、Wigner分布(Wigner-Ville Distribution, WVD)及改进的各类Wigner分布[4]100-106。STFT主要是对信号进行加窗截断处理,然后对截取的每段信号进行傅里叶变换[5]。WVD是信号的时频能量密度,信号的WVD分布存在交叉项干扰的问题[6]15-17,所以提出了一系列的改进算法,如伪Wigner-Ville分布(Pseudo Wigner-Ville Distribution, PWVD)、平滑伪Wigner-Ville分布(Smoothed Pseudo Wigner-Ville Distribution, SPWVD)、[6]70-82自适应最优核(Adaptive Optimal Kernel, AOK)时频分布以及SPWVD等分布的重排形式[6]112-116。 其中,AOK是一种改进可以有效抑制交叉项的WVD方法[7]。定义短时模糊函数为A(t;θ,τ),是窗函数截取的小段信号的模糊函数[7], (25) (26) 假设负重轮半径r=0.4m,其轮心位于(x3=1,y3=0,z3=-0.3)m处,距离Q点最近的负重轮上有4个微动散射点,分别位于4根辐条上,与z轴夹角分别为0,π/2,π,3π/2。可得改进模型与传统模型微多普勒频率随时间变化的理论对比,如图4所示。 分析图4可知:1)仿真结果与第1节结论相符,故为了表示履带式车辆不同部件的微多普勒变化规律,可将履带式车辆的运动模型简化为一个平动散射点和多个微动散射点的点散射模型,微动散射点分别位于负重轮轮辐、履带板和炮塔上;2)当车辆多普勒频率为fd时,微多普勒频率位于[0,2fd]区间内,同时履带AF段产生的微多普勒频率最大,为2fd;3)同一构件上不同微动散射点产生的微多普勒变化规律相同,但t=0时刻频率不同,故按照传统模型对履带及车轮圆周积分时,微多普勒频率将完全遍布于时频图上时间[0,t]和频率[0,2fd]的空间内,其变化规律将不可观测,估计车辆行进速度,车轮转动周期等参数十分困难,使用本文改进模型后,为有限个散射点,其规律将更容易观测,对微多普勒频率的刻画更为精细,更有利于相关参数的估计。 图4 履带式车辆微多普勒频率变化对比 为了比较不同时频分析方法的性能,对简化后的改进模型所得的雷达回波观测信号s(t)分别使用STFT、WVD、PWVD、SPWVD、重排的SPWVD及AOK来进行时频分析,结果如图5所示。 分析图5可知:1)对观测信号进行时频分析所得微多普勒与理论推导得出的微多普勒结果一致,验证了理论微多普勒频率推导及时频分析方法的有效性;2)所采用的时频分析方法中,STFT时频图的分辨率较低,WVD和PWVD时频图交叉项干扰特别严重,尤其是WVD时频图,信号自项完全被淹没在交叉项中,不可分辨,SPWVD和重排SPWVD时频图的分辨率比较高,但前者仍然存在少量的交叉项干扰,后者交叉项抑制能力更强但信号强度受到了一定的影响,AOK时频图也能在一定程度上抑制交叉项干扰,但其时频分辨率随之降低,同时部分微动信号也被抑制。综上所述,考虑到AOK和重排SPWVD存在计算复杂度更高的问题,笔者认为STFT和SPWVD是履带式车辆这类多微动散射点目标雷达回波效果比较好的时频分析方法。 为了验证本文改进模型的正确性,使用实测数据进行分析,利用某型车载雷达获得某坦克的雷达回波实测数据,对实测数据利用STFT进行时频分析,其时频图如图6所示。 图6 实测数据时频图 由图6可知:1)与仿真数据的微多普勒频率分布在[0,2fd]区间内一样,实测数据的微多普勒频率也分布在[0,2fd]区间内,在2fd处也存在明显的微动分量,即上履带板的微动,同时在[0,2fd]区间内存在正弦变化的微动分量,即负重轮的微动,即可初步判定该类目标属于带有负重轮的履带式车辆;2)通过实测数据的时频图可以看出,微多普勒频率并没有遍布于时频图空间内,其微动规律可观测,验证了仿真模型的有效性;3)主体多普勒频率约为150 Hz,根据式(4)可知车辆行进速度在雷达视线方向的速度为2.25 m/s,与实际情况相符。 [1] CHEN V C. The micro-Doppler effect in radar[M]. London: Artech House, 2011:18-20,60. [2] LI Y B, DU L, LIU H W. Noise robust classification of moving vehicles via micro-Doppler signatures[C]∥Maria Rey.2013 IEEE Radar Conference, Ottawa, April 29-May 3, Ontario,Cana-da.IEEE,2013:1-4. [3] 黄健,李欣,黄晓涛,等.基于微多普勒特征的坦克目标参数估计与身份识别[J].电子与信息学报,2010,32 (5):1050-1055. [4] 张群,罗迎.雷达目标微多普勒效应[M].北京:国防工业出版社,2013. [5] 王炳和.现代数字信号处理[M].西安:西安电子科技大学出版社,2011:251-254. [6] 葛哲学,陈仲生.MATLAB时频分析技术及其应用[M].北京:人民邮电出版社,2006. [7] 芮力,蒋涛,王德石,等. 基于自适应最优核时频分布理论的多分量LFM信号参数估计[J]. 海军工程大学学报, 2011, 23(6):91-95. [8] CHEN V C.Advances in applications of radar micro-Doppler sig-natures[C]∥Christian Pichot.2014 IEEE Conference on Antenna Measurements & Applications,November 16-19,Antibes Juan-les-Pins,France.IEEE,2014:1-4. [9] 张万君,牛敏杰,杨雨迎,等.基于最优核时频分布的装甲车辆微多普勒特征分析[J].火力与指挥控制,2015, 40(6):14-17. [10] 骆宇峰.SAR轮式/履带式车辆微多普勒建模和特征分析[D].杭州:杭州电子科技大学,2012:21-37. (责任编辑: 牛燕平) RadarMicro-DopplerEffectBasedonImprovedMicroMotionModelofTrackVehicle YUN Le-ying1, LÜ Jun1, LI Tong1, WANG Xi1, LIU Lei2 (1. Department of Information Engineering, Academy of Armored Force Engineering, Beijing100072, China;2. Troop No.63752of PLA, Weinan714000, China) There are several problems of the current micro-motion model of track vehicle, for example, the specific structure of the track, the relationship between radar and vehicle space position and the crawler effect of the track shoe are ignored. Aiming at these problems, an improved model is established in this paper by analyzing the structure and motion characteristics of track vehicle and the working principle of radar. It is much finer to express micro-Doppler frequency comparing to the existed. In order to analyze the Doppler and micro-Doppler effects of track vehicle, the radar observation signals generated by the translation of body part and micro motion parts are obtained by simulation, time-frequency analysis is carried out to the simulation signal by six different methods, respectively, Short Time Fourier Transform(STFT), Wigner-Ville Distribution(WVD), Pseudo Wigner-Ville Distribution(PWVD), Smoothed Pseudo Wigner-Ville Distribution(SPWVD), Adaptive Optimal Kernel(AOK) Time-Frequency Distribution and reassignment Smoothed Pseudo Wigner-Ville Distribution. The performance of these methods to analyze micro-Doppler signals of track vehicle is compared in both time-frequency resolution and cross-item size. Finally, the measured data test is carried out, actual observability of the micro-Doppler effect and the correctness of the improved model are verified by comparing with the simulated result of the traditional and improved model. track vehicle; micro-motion model; micro-Doppler effect; time-frequency analysis; radar echo 1672-1497(2017)04-0093-07 2017-03-15 贠乐应(1993-),男,硕士研究生。 TN95 :ADOI:10.3969/j.issn.1672-1497.2017.04.018

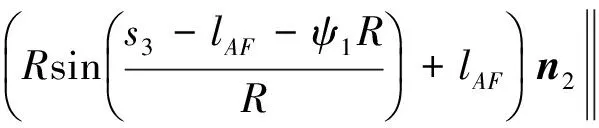
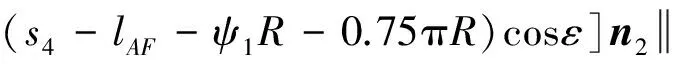

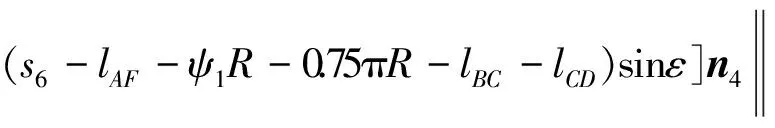
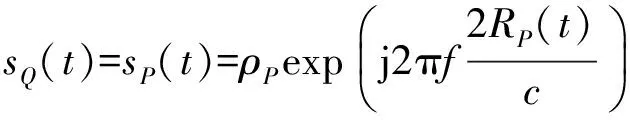
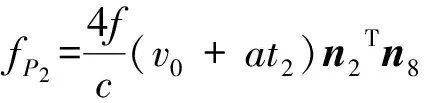
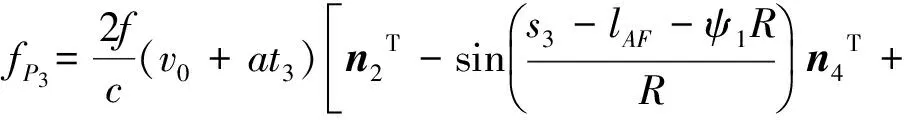
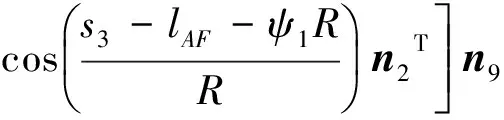



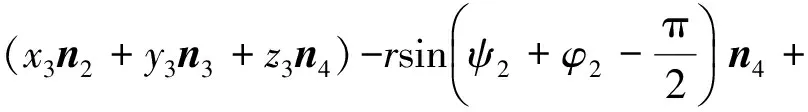


2 时频分析
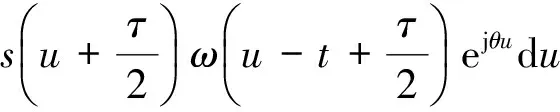

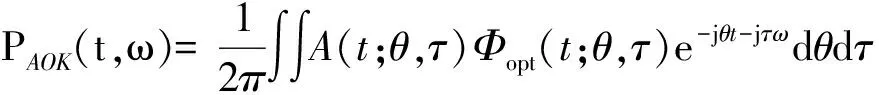
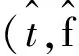
3 仿真分析

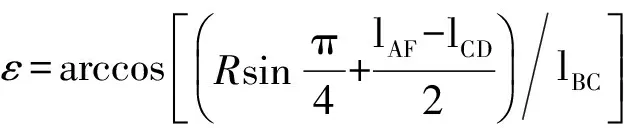

4 实测数据分析

