考虑优先度的战时装备物资调度模型

包 博， 李体方， 张 搏

(空军工程大学防空反导学院， 陕西 西安 710051)

考虑优先度的战时装备物资调度模型

包 博， 李体方， 张 搏

(空军工程大学防空反导学院， 陕西 西安710051)

针对战时装备物资调度问题，提出了一种基于遗传算法的装备物资调度模型。该模型依据战时装备物资保障任务需求的特点，以时间短、费用小、风险低为目标准则，引入需求点优先度实现有重点地调度装备物资，并采用遗传算法来求解模型。最后，结合算例验证了模型的可行性和有效性，为战时装备物资调度决策提供了思路。

战时装备物资； 调度模型； 遗传算法； 优先度

目前，针对军事物资调度问题的相关研究多是基于运筹学的运输问题模型，并主要在目标准则、约束条件及调度背景规则等方面进行了深入探讨[1-2]。如：张来顺等[3]提出了一种基于多重约束整合的航空油料模型，较好地处理了多目标、多参数约束的物资调度和运输问题；陈莹珍等[4]针对救灾物资调运问题，基于公平原则构建了应急物资分配模型；针对多供应点、多需求点的物资调运问题，林勇等[5]提出了一种基于综合评价函数的调度模型，魏国强等[6]在对各需求点进行优先排序和分类的基础上，提出了一种多目标模糊规划模型。上述研究在模型构建中均系统地考虑了多方面的目标要求，但在调度决策中仍未考虑需求点重要度的区分问题，认为各需求点同等重要，这是不合理的。

笔者在分析战时装备物资调度任务需求特点的基础上，兼顾时间、费用和风险3个目标，构建了战时装备物资调度模型，提出采用需求点优先度来区分各需求点的优先保障程度，进而实现有重点地调度装备物资，并采用遗传算法来求解调度模型。

1 战时装备物资调度模型构建

1.1问题描述

战时装备物资调度要求具备快速集中地处理大量物流的能力，且在调度目标上更加侧重于保障的快速性和可靠性[7-8]。战时装备物资调度决策必须从全局保障效果出发，并兼顾多方面的目标要求，有重点地安排调度任务。

为方便研究，将战时装备物资调度问题简化为m个供应点(A1,A2,…,Am)向n个需求点(B1,B2,…,Bn)调运l类(S1,S2,…,Sl)装备物资，其中：xijk为供应点Ai(i=1,2,…,m)调运至需求点Bj(j=1,2,…,n)的第k(k=1,2,…,l)类装备物资的数量；ajk为第j个需求点对第k类装备物资的需求量；bik为第i个供应点对第k类装备物资的最大保障量。tij、rij、cij分别为Ai至Bj的调运时间、运输可靠度和单位装备物资调运费用，其中：tij是指各供应点到需求点的运输时间；rij是指在自然条件或敌方袭扰等诸多不确定风险下，按规定运达的可能性，用来度量运输风险；cij是指每单位装备物资对应的调运费用。

制定调度方案就是确定各供应点配置到各需求点的各类装备物资的数量，则调度方案U为

(1)

式中：uij={xij1,xij2,…,xijl}，为供应点Ai向需求点Bj调运的不同种类装备物资数量的集合。

在建模时进行如下假设：

1)各供应点的运输能力无限制；

2)总体上供大于求，供应点能满足需求点对装备物资的需求；

3)调度方式仅限于从供应点到需求点；

4)装备物资需求量和最大保障量确定；

5)运输费用根据货物单位量计算，装备物资运输量及供需量均为整数。

1.2需求点优先度

需求点优先度hj(j=1,2,…,n)是用来衡量需求点优先保障程度的参数。基于最大程度地维持与恢复装备整体战斗力的原则，笔者在调度决策中，从需求点的战略重要程度(y1)、任务紧迫程度(y2)、受损程度(y3)、装备物资存量短缺程度(y4)和承受打击程度(y5)五个方面，对需求点优先度进行综合评价,进而区分保障重点。理想点法是一种有效的多属性决策方法，能够对备选方案进行评价与排序，因此，笔者采用理想点法来确定各需求点的优先度[9-10]。具体步骤如下：

1)选取需求点优先度主要评价指标，记评价指标集为y={y1,y2,…,yp},p=1,2,…,5。

2)采用层次分析法确定各指标权重，得到权重向量W=(W1,W2,…,Wp)。

3)邀请专家对需求点Bj进行评价，得到评价矩阵，并对评价矩阵进行无量纲化和指标加权处理，得到加权评价矩阵Y。

4)确定参考的正、负理想点。正、负理想点分别由各指标的最大、最小值构成，其中：

(2)

(3)

5)计算各需求点到正、负理想点的欧氏距离，即需求点与正、负理想点的贴近度Lj、Dj，进而得到需求点优先度Zj，其中：

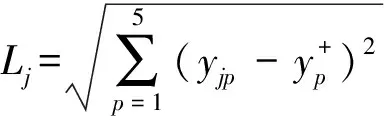
(4)

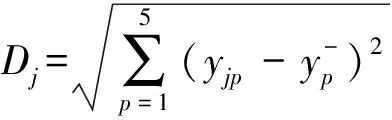
(5)

Zj=Dj/(Lj+Dj),0≤Zj≤1。

(6)

当Zj→1时,表明该需求点的优先保障程度越高。

1.3调度模型

1.3.1 多目标调度模型

从系统整体角度出发，结合需求点优先度，以总费用最小、总时间最短、总风险最低为优化目标建立装备物资调度数学模型，即

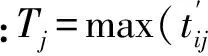
(10)

式(10)中：tijk为第k类装备物资从供应点Ai到需求点Bj的运输时间。

对模型说明如下：式(7)表示在战时进行装备物资调度时，需保证费用的合理性；式(8)表示在满足总体调运时间最短的同时，也保证了优先需求点的调度时间尽可能地缩短；式(9)表示在满足调度整体风险最低的同时，也保证了优先需求点的调度风险尽可能地降低。

1.3.2 单目标调度模型

采用指数加权的方法将多目标优化问题转化为单目标优化问题，得到单目标装备物资调度数学模型为

minf=min(C(U)w1T(U)w2E(U)w3),(11)

式(11)中w1、w2、w3为3个子目标函数的权重，采用德尔菲法确定；式(12)表示将最大保障量、需求量及运输量限定为自然数；式(13)表示各类装备物资调运总量都等于需求总量，且最大保障总量不小于需求总量；式(14)-(17)分别表示对调运时间、单位调运费用、可靠度及优先度进行约束。

2 基于遗传算法的调度模型求解

该调度模型为多个约束条件组合的优化问题，遗传算法对于该类问题具有良好的求解能力，且易于实现[11-12]。因此，笔者应用遗传算法来求解模型，并结合模型特点进行算法设计。

2.1染色体编码

依据模型约束特点，采用整数编码方式对染色体进行编码。对于该类有m个供应点、n个需求点和l种装备物资的调运问题，染色体采用长度为“m×n×l”的整数串表示。如针对“2×3×2”问题，染色体编码为

(5,0,3,5,0,5,5,3,6,0,2,6)。

染色体的1-2位表示2个供应点向需求点B1调运的第1种装备物资量，3-4位表示2个供应点向需求点B2调运的第1种装备物资量，5-6位表示需求点B3的装备物资调运量，后6位为第2种装备物资的调运量。该染色体可解码为如下决策矩阵：

2.2适应度值计算

适应度值越小，该染色体越好。依据式(11)可得适应度值计算公式为

fitness=C(U)w1T(U)w2E(U)w3。

(18)

2.3选择、交叉和变异操作

笔者采用轮盘赌的选择方式，依据适应度值选择染色体，染色体的适应度值越好，被选中的概率越大，概率计算公式为

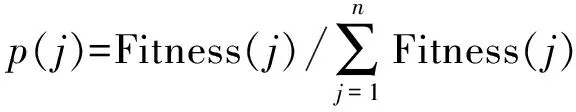
(19)

Fitness(j)=1/fitness(j)。

(20)

进行交叉操作时，首先以一定概率从种群中随机选取2个染色体，并依据供应点数量分段进行交叉操作。以“2×3×2”问题为例，将染色体分成6段，对第5段即9-10位进行交叉，则

该操作的好处在于能够满足需求点总量的约束条件。但交叉操作后某些供应点的供应量超出其最大保障量，为保证染色体的合法性，采取如下调整操作：计算供应量超出最大保障量的供应点数量，选择该供应点目前供应量最大的需求点，减去超出量，同时从其他供应点增加相同数量的装备物资调运至该需求点，如：设供应点2的最大可供应量为8，而染色体中供应总量为9(第2、4、6位之和)，对第2位采取减1操作，同时对第1位采取加1操作，即

变异操作随机选择变异染色体，对该染色体随机选择两点进行交叉操作，并对非法染色体采取调整操作使染色体满足约束，如交叉位置为3和4的变异操作为

2.4算法实现

应用遗传算法求解调度模型的具体步骤如下：

1)设置算法相关参数，并进行种群初始化；

2)计算当前种群中染色体的适应度值；

3)依据染色体的适应度值，对种群进行选择、交叉和变异操作，产生新的种群；

4)每次循环迭代后，判断是否满足终止条件，若满足终止条件，则终止循环并输出结果；否则返回步骤2)，重复循环操作。

3 算例分析

3.1算例

设有5个地空导弹部队，对3种装备物资提出了不同的需求量，可由4个供应点进行装备物资调运，需制定出合理的装备物资调运决策方案。各需求点的需求量及各供应点的最大保障量如表1、2所示。采用理想点法确定各需求点的优先度为Z1=(B1，B2，B3，B4，B5)=(0.6，0.4，0.7，1，0.8)。各供应点到需求点之间的单位调运费用、调运时间和可靠度(运输风险)如表3所示。为处理方便，笔者对表1-3中的数据不具体设置单位，以数量单位表示。

表1 各需求点的需求量

表2 各供应点的最大保障量

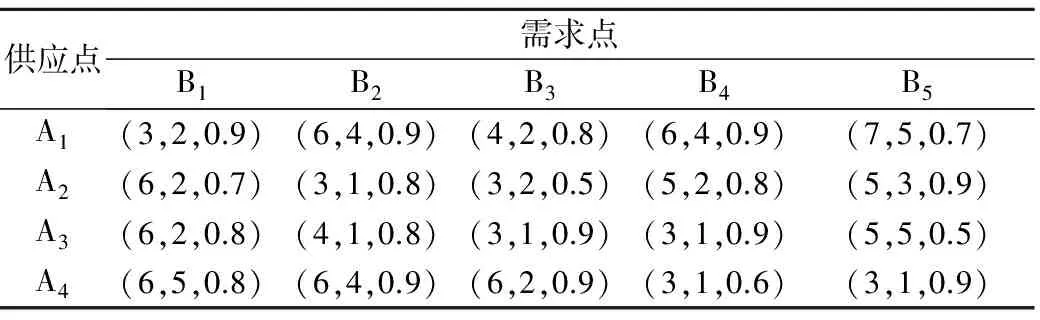
表3 各供应点到需求点之间的单位调运费用、调运时间和可靠度

3.2仿真实验及结果分析

3.2.1 参数设置

采用德尔菲法确定目标函数中单位调运费用、调运时间和可靠度(运输风险)的权重向量为w=(0.2,0.5,0.3)。设遗传算法中交叉概率为0.6，变异概率为0.4。

3.2.2 仿真结果分析

通过寻优计算，得到战时地空导弹装备物资调运决策方案Ⅰ，如表4所示,其中：uij表示从供应点Ai到需求点Bj调运的3种装备物资的数量。该方案满足数量约束，综合权衡了各优化目标的要求，在寻优求解过程中，对优先度高的需求点，其调运时间相对更短、可靠度相对更高。

该算例的最优目标函数值为11.358，相应的适应度收敛曲线如图1所示。

表4 调运决策方案Ⅰ

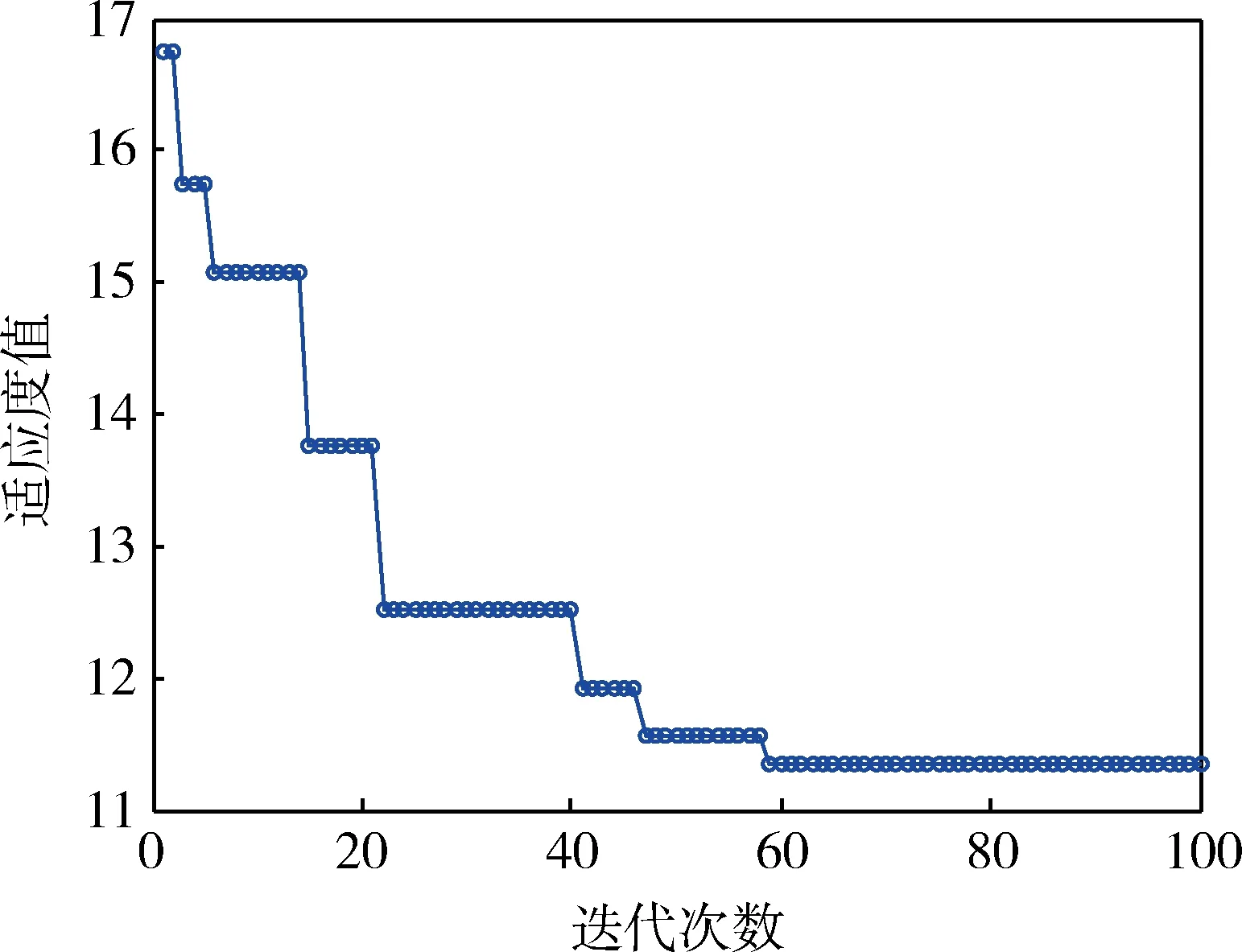
图1 适应度收敛曲线

3.2.3 优先度参数分析

为了探讨需求点优先度对调度决策的影响，基于上述算例，设定另一组优先度参数Z2=(B1，B2，B3，B4，B5)=(1，0.1，0.1，0.1，0.1)，其他参数相同，据此制定调运决策方案，并对两组结果进行对比。

通过寻优求解，得到表5所示的调运决策方案 Ⅱ。

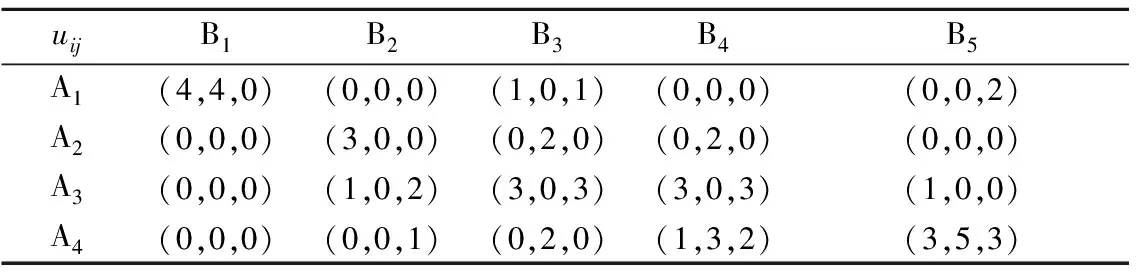
表5 调运决策方案Ⅱ

由表5可以看出：需求点优先度参数能够在调度决策中有效地区分保障优先度高的需求点。如：需求点B1的3种物资需求均来自于供应点A1。这是由于B1的优先度较高，B1的调运决策结果对于整体的调运效果影响相对较大，因而在调运决策中将会优先考虑该需求点。同时，相对于其他供应点，供应点A1保障需求点B1的单位调运费用最低，时间较短，风险较低，因而出现需求点B1的3种物资需求均来自于供应点A1的情况。需求优先度参数通过对全局重点保障需求点的有效区分，达到了提升整体调度效果的目的。

4 结论

笔者针对装备物资调度问题进行了研究，提出一种考虑优先度的战时装备物资调度模型，为战时装备物资调度决策提供了一种新思路。提出的优先度概念能够在调运决策中从全局出发区分重点保障需求点。下一步，将更加全面地分析需求点重要度的影响因素，探究更加精确的重要程度差异描述方法，同时，结合调运决策模型特点设计更为准确、稳定的求解算法。

[1] 曹继平,宋建社,朱昱,等.战场抢修多需求点多资源优化调度研究[J].兵工学报,2008,29(8):995-1000.

[2] 卢昱,陈兴凯,韩震.战时网络化物资调度建模[J].装甲兵工程学院学报,2016,30(1):21-24.

[3] 张来顺,王瑛,姚頔,等.基于多重约束整合模型的航空油料调运优化[J].空军工程大学学报(自然科学版),2011,12(3):6-10.

[4] 陈莹珍,赵秋红.基于公平原则的应急物资分配模型与算法[J].系统工程理论与实践,2015,35(12):3065-3073.

[5] 林勇,姜大立,张立,等.多供应点和多需求点应急物资调运模型及算法[J].计算机应用研究,2016,5(5):1293-1297.

[6] 魏国强,余超.带模糊参数的战时紧缺资源调度模型[J].计算机工程与应用,2013,49(12):246-249.

[7] 王铁宁,梁波,曹钰.基于多资源点的装备应急器材调度决策模型[J].装甲兵工程学院学报,2012,26(6):10-14.

[8] 董鹏,杨超,罗朝晖.战区多需求点装备物资紧急调运模型及算法[J].火力与指挥控制,2012,37(10):27-31.

[9] 马亚龙.评估理论和方法及其军事应用[M].北京:国防工业出版社,2013:68-70.

[10] 阳林,刘付显,张搏. 基于理想点法的区域防空部署优化方法[J]. 空军工程大学学报(自然科学版),2014,15(2):49-52.

[11] 陈进,龚时雨.基于遗传算法的作战资源优化分配[J].科学技术与工程,2013,13(29):8647-8658.

[12] 于双双,王铁宁,李宁.装备器材保障资源调度决策模型及算法[J].火力与指挥控制,2016,41(7):71-76.

(责任编辑: 王生凤)

EquipmentMaterialSchedulingModelinWartimewithPriority

BAO Bo, LI Ti-fang, ZHANG Bo

(Air Defense and Anti-missile College, Air Force Engineering University, Xi’an710051, China)

In view of the problem of the equipment material scheduling in wartime, an equipment material scheduling model based on genetic algorithm is proposed. This model is based on the characteristics of the equipment material scheduling tasks in wartime, in pursuit of less time, less cost, less risk as the target criterion, introducing the priority of demand points to realize the priority of scheduling equipment material. The genetic algorithm is used to calculate the scheduling model. Combined with an example, the feasibility and effectiveness of this model are verified, which provides a new method for the decision making of the equipment material scheduling in wartime.

equipment material in wartime; scheduling model; genetic algorithm; priority

1672-1497(2017)04-0041-05

2016-12-13

包 博(1993-)，男，硕士研究生。

E075；TJ089

：ADOI：10.3969/j.issn.1672-1497.2017.04.008