基于多方向像素连续折叠机制与Radon变换的图像加密算法
2017-09-15孙力黄正谦项振茂
孙力,黄正谦,项振茂
(1. 浙江警察学院计算机与信息技术系,浙江 杭州 310053;2. 浙江大学计算机科学与技术学院,浙江 杭州 310027)
基于多方向像素连续折叠机制与Radon变换的图像加密算法
孙力1,黄正谦2,项振茂1
(1. 浙江警察学院计算机与信息技术系,浙江 杭州 310053;2. 浙江大学计算机科学与技术学院,浙江 杭州 310027)
提出了基于多方向像素连续折叠机制与Radon变换的图像加密算法,从不同的方向、利用不同的像素扩散技术来加密明文,显著消除密文周期性。首先,对初始明文完成均等分割,获取左、右两个子块;引入Radon变换机制,对左、右子块进行0°~180°的Radon变换,获取对应的Radon投影谱图像;利用Arnold映射、引力模型分别混淆左、右子块的Radon谱图像,获取两个子置乱密文,将二者进行组合,输出完整的置乱图像。为了从空间多个方向来扩散像素,设计了4个方向连续折叠机制,利用4个不同方向对应的扩散函数来改变像素值,实现图像加密。实验结果表明,与当前图像加密技术相比,所提算法具有更高的安全性与抗攻击能力,输出密文的像素分布更加均匀。
图像加密;多方向像素连续折叠;Radon变换;Radon投影谱;Arnold映射;引力模型
1 引言
随着网络技术与计算机技术的日益发展,多媒体技术在日常生活中占据重要地位,已成为当前各用户沟通的常用手段。图像因其具备良好的直观表达能力,给人们的生活带来了极大的方便。但是,因图像包含丰富的用户信息,在网络传输中容易遇到外来攻击,这导致图像内容真实性受到严重威胁,图像信息易被篡改与窃取,给用户信息安全带来巨大隐患[1,2]。因此,采取某种手段来保护图像在网络中避免遭受攻击,已是当前世界各国的关注焦点。然而,传统的数据保密技术,如DES、IDEA和RSA算法等,忽略了图像冗余与大容量的特点,不适合用于数字图像的保密[3]。因此,有必要设计专门用于图像的加密技术。近年来,随着混沌系统的出现与应用的完善,给数字图像保密技术的研究提供了新的技术方向,刘会等人[4]为了提高图像信息的安全性,提出了基于量子混沌映射的高效安全的图像加密算法,利用Logistic映射来生成二维Arnold变换的初始条件,通过迭代该变换,对输入明文完成像素置乱,且设计了量子混沌系统,对置乱图像进行扩散,改变像素值,实验结果验证了其算法的有效性与优异性。Tang等人[5]为了改善数字图像在网络传输的抗攻击能力,设计了随机投影分割与混沌系统的图像加密技术,该技术实现将明文分割为若干个重叠子块,利用投影分割方案将每个子块划分为投影线,通过迭代混沌系统所输出的混沌序列,结合XOR算子,实现图像加密,实验结果验证了其算法的有效性。Li等人[6]为了解决低维混沌映射的不足,并提高密文的抗攻击能力,提出了基于像素水平置乱与位水平扩散的差超混沌图像加密技术,设计了一种5D超混沌系统,结合明文像素生成一组密钥流,从而构建了像素混淆机制,从像素水平来实现明文置乱,再利用像素扩散技术,从位水平上改变像素值,显著提高密文的安全性,实验结果表明其算法具备更高的安全性以及更强的抗明文攻击能力。
利用混沌系统来实现明文加密,主要是充分利用其复杂相空间以及混沌行为来完成像素置乱与扩散,有较好的加密安全性,能够保护图像在网络中的安全传输。但是,当前混沌加密技术在其像素混淆与扩散两个阶段,都是利用了相同的置乱与加密机制,并从单一的方向来完成,这导致密文存在明显的周期性,使得这些算法的安全性有待进一步提高。
针对上述问题,本文提出了基于多方向像素连续折叠机制与Radon变换的图像加密算法。利用Radon变换机制对明文分割后形成的左、右两个子块进行0°~180°的Radon变换,得到两个Radon投影谱图像;再利用Arnold映射、引力模型,分别混淆左、右子块的Radon谱图像,获取置乱图像,通过不同的置乱操作,有效降低了置乱周期性;同时,设计了4个方向连续折叠机制,利用不同的扩散函数从4个方向改变像素值,显著降低扩散周期性。最后,测试了所提加密技术的安全性。
2 Radon变换
Radon变换[7]具有较强的抗噪性能,在数字图像处理领域被广泛应用,图像经过Radon变换后,能够获取一幅与初始图像完全不同的投影谱。因此,Radon变换可以混淆图像内容,能够较好地隐秘图像信息、迎合加密技术的要求。令尺寸为M×N的明文为f( x, y),则其Radon变换[7]为:


图1 直线表示
由式(1)可知,Radon变换可表征为f( x, y)沿着直线L的线积分。也就是将f( x, y)在某个方向进行投影后所输出的结果。先固定角度θ,取所有的t值,可输出f( x, y)在θ方向的投影结果;再改变θ,从而可得到任意角度的投影值。
根据参考文献[7]可知,在图像应用领域,Radon变换具备以下特点[7]。
· 若(x, y)是图像f( x, y)空域中的像素点,则其在频域内的直线可表示为:

· 若(ρ0,θ0)是图像f( x, y )频域中的像素点,则其在空域内的直线可表示为:

· f( x, y)的平移能够让其对应的投影谱同样具备平移特性。若 kx、ky分别是(x, y)在x轴、y轴上的平移长度,则有:
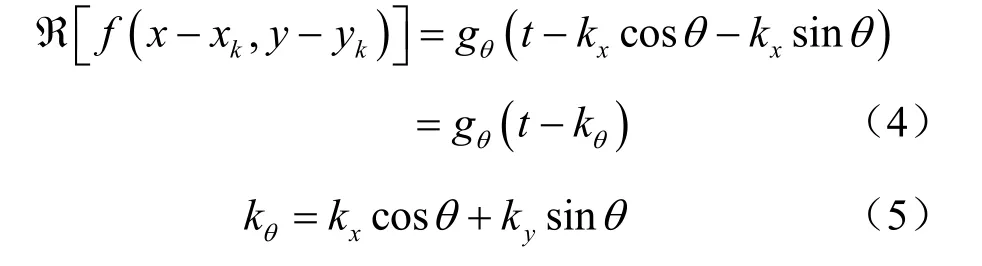
根据上述性质可知,对于空域图像f( x, y ),通过Radon变换,可将其变换为频域,获取投影谱,实现像素混淆。以图 2(a)为例,利用 Radon变换后,输出的投影谱如图 2(b)和图 2(c)所示。图2(b)是特定θ为50°时的变换结果;而图2(c)是θ为0°~180°的投影集合形成的谱图像。由图2可知,初始明文经过0°~180°的Radon变换后,输出一个与初始明文截然不同的投影谱,如图 2(c)所示。这个投影谱充分隐秘了图像信息,可用于数字图像加密。

图2 Radon变换的投影谱
3 图像加密算法设计
为了尽可能地降低加密周期性,本文针对置乱与扩散两个阶段,利用不同的加密操作并考虑不同的加密方向,设计了一种新的图像加密技术,加密算法过程如图3所示。由图3可知,所提加密技术主要分为两个阶段:基于多混沌映射与加密算法变换的明文置乱和基于4个方向连续折叠机制的图像扩散。

图3 本文图像加密算法过程
3.1 基于多混沌映射与Radon变换的明文置乱
(1)令初始图像为f( x, y),其尺寸为M×N。首先,将f( x, y)分割为两个尺寸相等的子块fL(x, y)和fR(x, y )。然后,再利用上述Radon变换对左、右子块fL(x, y)和fR(x, y )进行 0°~180°投影变换,获取两个Radon谱图像。
(2)利用二维 Arnold映射[8]来提高左子块fL(x, y)的 Radon谱图像的像素置乱度,获取相应的置乱结果f'L(x, y ):
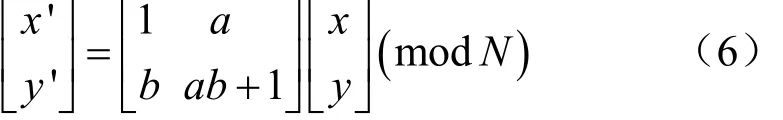
其中,(x', y ')、(x, y)分别是 Arnold映射变换后、前的像素位置;a、b 为用户参数,本文取a=1、b=1; N是图像矩阵阶数,本文取N=256。
(3)随后,再引入重力模型[9]来混淆右子块fR(x, y)的 Radon谱图像,得到相应的置乱结果f'R(x, y):


其中,G代表重力系数;m( x, y, z)是空间粒子P的质量;(x, y, z)是粒子P的空间位置,如图4所示;m( i, j)是右子块fR(x, y)的 Radon谱图像的像素质量;Bij、B'ij分别是置乱前、后的像素位置。为了确保式(7)的分母不为零,令z≠0。

图4 图像在空间内的平面映射
(4)获取左右子块fL(x, y)和fR(x, y )的Radon谱图像的置乱结果f'L(x, y)和f'R(x, y )后,将二者进行组合,形成完整的置乱图像f'(x, y )。
以图5(a)为例,对其进行均等分割,如图5(b)和图5(c)所示。利用Radon变换处理后,获取的Radon谱如图5(d)和图5(e)所示,经过Radon变换处理后,图像的信息被初步混淆,有效掩盖了明文内容;左、右子块再经过Arnold映射与引力模型置乱后,输出两个与Radon谱图像截然不同的结果,图像信息的混淆程度得到进一步提高,完全隐秘了图像内容,如图5(f)和图5(g)所示。由图5(f)和图5(g)可知,二者视觉存在较大差异,通过不同的低维映射来置乱,降低了整个图像的像素相关性。
3.2 基于4个方向连续折叠机制的图像扩散
图像经过混沌映射与Radon变换处理后,仅改变了其像素位置,但其像素值并未发生变化,导致其置乱密文的安全性不佳。为此,本文设计了4个方向连续折叠机制,从多个方向来完成像素扩散。为了增强扩散机制与混沌理论、明文像素的关联度,本文首先利用 Logistic映射来形成密钥流,以此来设计扩散函数。Logistic映射可表示为[10]:

其中,λ∈[0,4]是混沌参数; xi是变量。
为了改善密文的抗明文攻击能力,本文利用明文像素来生成式(9)的初值 x0:

其中,Z为明文像素总量。
利用 x0与λ来迭代式(9),形成混沌序列{xi},i=1,2,…,M×N ;并利用{xi}建立一个量化模型,得到密钥流{ki}:

再基于{ki},设计基于 4个方向连续折叠机制的图像扩散方法,步骤如下。
(1)将置乱图像f'(x, y)的所有像素变为一个矩阵T;同时,将{ki}也变为与T具有相同维数的矩阵Q。先将矩阵T按照图 6(a)的方向进行折叠,其对应的扩散模型为:


图5 初始图像的置乱结果
其中,Wh(i, j)、Bh(i, j)是T的上半部分、下半部分中(i, j)处的元素;Qh(i, j)是Q上半部分中(i, j)处的元素;W'h(i, j)、B'h(i, j)是Wh(i, j)、Bh(i, j)加密后的像素值。
(2)利用式(12)加密后,可形成第1个密文 I1';随后,利用 I1',完成图6(b)的第2个方向的扩散:

其中,Wr(i, j)是 I1'的右上半部分中(i, j)处的元素;Bl( i, j)是 I1'的左下半部分中(i, j)处的元素;Qtr(i, j)是Q的右上半部分中(i, j)处的元素;W'r(i, j)、B'l(i, j)是Wr(i, j)、Bl( i, j)加密后的像素值。
(3)利用式(13)加密后,可形成第2个密文 I2';随后,利用 I2',完成图6(c)的第3个方向的扩散:

其中,Rh(i, j)、Lh(i, j)是 I2'右半部分、左半部分中(i, j)处的元素;Qrh(i, j)是Q的右半部分中(i, j)处的元素;R'h(i, j)、L'h(i, j)是Rh(i, j)、Lh(i, j)加密后的像素值。
(4)利用式(14)加密后,可形成第3个密文 I3';随后,利用 I3',完成图 6(d)的第 4个方向的扩散:

其中,Lt( i, j)、Rb(i, j)是 I3'左上部分、右下部分中(i, j)处的元素,Qrb(i, j)是Q右下半部分中(i, j)处的元素;R'b(i, j)、L't(i, j)是Rb(i, j)、Lt( i, j)加密后像素值。
利用式(12)~式(15)对置乱图像经过4次加密后,形成扩散密文 I4'。以图5(h)为样本,利用式(12)~式(15)对其完成加密后,获取的扩散密文如图6(e)所示。由图6(e)可知,利用多方向连续折叠扩散技术处理后,形成的加密结果与图5(h)之间存在巨大差异。
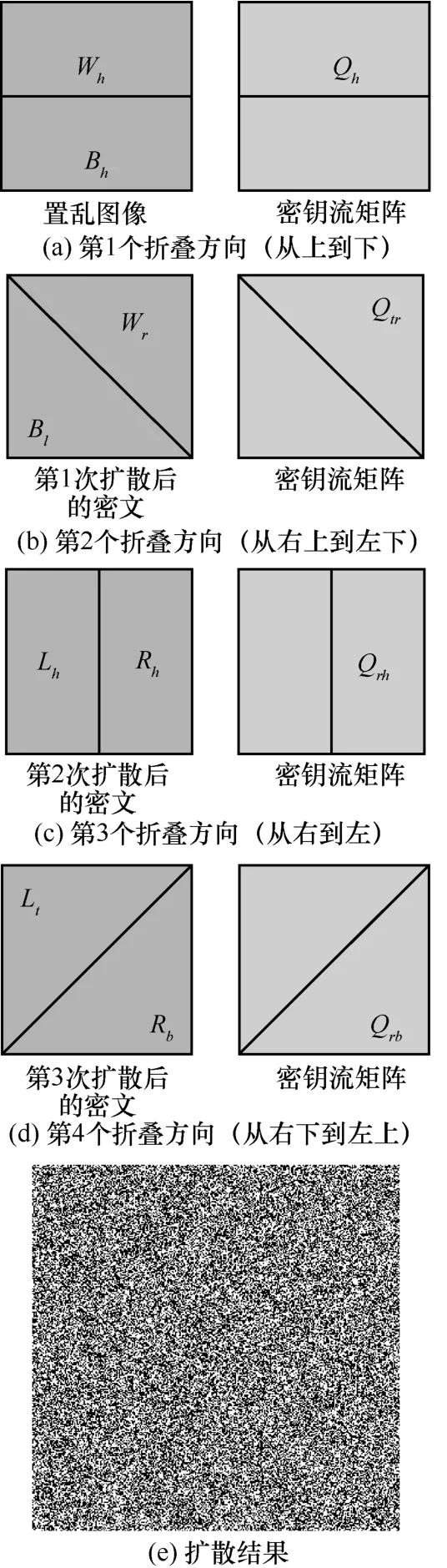
图6 基于4个方向折叠机制的扩散
4 实验结果与分析
为了测试所提加密方法的合理性与优异性,借助MATLAB软件来完成实验,同时,将当前安全性较高的混沌加密算法作为对照组:参考文献[6]算法和参考文献[11]算法。用 MATLAB仿真软件测试这些算法性能。测试条件为:Intel 3.5GHz、双核CPU、4 GB内存,Windows XP系统。算法部分参数为:a=1,b=1,N=256,Radon变换的角度间隔为1°,λ=3,
4.1 加密效果
以大小为 256 dpi×256 dpi的灰度明文为测试样本,如图7(a)所示,再利用本文算法、参考文献[6]算法、参考文献[11]算法对其完成加密处理,效果如图 7(b)~图 7(d)所示。由测试效果可知,初始图像经过3种加密技术处理后,其内容信息均被充分隐藏,呈现一幅重度噪声干扰图像,攻击者无法轻易从中获取任何线索,具备较高的视觉保密效果。为了彰显所提技术的优势,本文引入密文熵值[12]来量化 3种算法对应密文的安全性,计算数据见表1。

图7 3种加密技术对应的密文

表1 各算法对应的密文熵值测试结果
根据所得的熵值可知,虽然3种算法的密文熵值均与理论值8较为接近,但是本文加密技术的输出密文熵值最大,达到了7.999 2,而参考文献[6]、参考文献[11]的熵值分别为7.998 4、7.996 5。这表明本文所提加密方法的保密安全性更高,其密文具有更强的抗攻击能力。主要原因是本文算法从密文周期性出发,利用Radon变换来提高两个子块的像素混淆程度,且借助Arnold映射、引力模型对两个Radon谱进行独立置乱,提高了密文的随机度与复杂度,有效降低了置乱周期性,同时,利用明文像素自身特性来设计了4个方向连续折叠扩散机制,利用4个不同的加密函数从4个方向来改变像素值,在消除扩散周期性的同时,提高了密文与明文的联系,改善了算法的抗明文攻击能力。而参考文献[6]由于使用了5D超混沌系统来实现像素的置乱与扩散,通过增加算法复杂度的代价来提高密文安全性,使其密文安全性要高于参考文献[11]的技术,但是二者在像素的置乱与扩散阶段,均是利用相同的置乱、扩散函数,从单一方向来实现加密,使其输出密文存在较为显著的周期性,降低了算法的安全性。
4.2 密文相关性
图像相邻两像素间的关系紧密度对算法的保密性影响较大,通常,图像像素分布均匀,则其相邻像素的相关性较弱,反之,则相关性较大,容易给攻击者留下破译的线索,对密文安全性产生较大的威胁,因此,优异的加密算法应能充分消除这种相关性,使其像素分布达到均匀程度[12]。为了验证所提加密技术所输出密文相邻像素的相关性,从图7(b)~图7(d)中挑选3 000对相邻像素来测试,利用相关系数Cxy来评估[12]:

3种算法在水平方向上的Cxy统计结果如图8所示。由图 8(a)可知,未经加密的图像相邻像素之间的相关性很高,其像素分布的均匀度很不理想,整个图像的像素都叠加为对角线,对应的Cxy=0.967 4;但是,利用本文算法、参考文献[6]算法、参考文献[11]算法的加密方案对其处理后,这种对角线分布状态变为均匀分布,Cxy分别为0.0023、0.0038、0.0061。然而,综合图 8(b)~图 8(d)可知,本文加密机制的密文像素分布均匀度最高,没有出现像素叠加与空白效应,要优于参考文献[6]和参考文献[11]算法。

图8 加密前后的密文像素之间的相关性测试
不同方向的Cxy值统计结果见表2。由表2可知,就任意一个方向,明文的Cxy值始终是最大的,这也说明其相关性是最大的。然而,利用所提技术与参考文献[6]、参考文献[11]加密后,这种不利因素被充分削弱,Cxy明显降低,在3种加密机制中,本文算法的密文Cxy值始终是最低的。

表2 不同方向的Cxy值统计结果
4.3 抗明文攻击能力对比测试
在未知网络中传输图像时,选择明文攻击对其安全性威胁较大,因此,数字图像加密技术应该具备较强的抗明文攻击能力,确保密文安全传输[13]。根据国内外研究成果可知,像素变化率NPCR与平均变化响度(UACI)是评估图像加密技术抗明文攻击能力的有效指标[14]。为此,利用参考文献[14]的计算方法,得到本文算法、参考文献[6]算法、参考文献[11]算法3种技术的抗明文攻击能力评估结果,如图 9所示。根据测试结果可知,所提加密技术的NPCR、UACI的值均要高于参考文献[6]与参考文献[11]的值,且分别为99.83%、34.58%。其原因是本文利用Radon变换与混沌映射对明文完成了双重置乱,降低其置乱周期性,且利用明文像素来生成一组密钥流,从多个方向来扩散图像,使得整个图像加密过程与明文密切相关,从而提高了密文的抗明文攻击能力。而参考文献[6]、参考文献[11]两种算法的加密过程均忽略了明文自身特性,单纯地利用混沌理论来实现图像加密,使其输出密文的抗明文攻击能力不理想。

图9 3种算法的抗明文攻击能力量化测试结果
5 结束语
为了从多个方向提高像素的扩散程度,本文设计了基于多方向像素连续折叠机制与Radon变换的图像加密算法。引入Radon变换机制,对明文均等分割后的左、右子块进行0°~180°的Radon变换,输出两个Radon投影谱;再利用Arnold映射与引力模型对二者进行交叉独立置乱;设计 4个方向连续折叠机制,利用 4个不同方向对应的扩散函数来改变像素值,实现图像加密,从而有效地提高了密文安全性,且充分降低了密文周期性。通过与当前混沌加密技术进行对比测试,验证了本文所提加密机制的安全性与优异性。
[1] 韩珂, 张泽中. 基于雅克比椭圆混沌映射的图像加密算法研究[J]. 计算机仿真, 2014, 10(9): 187-192. HAN K, ZHANG Z Z. Study on image encryption algorithm based on Jacobian elliptic chaotic map[J]. Computer Simulation, 2014, 10(9): 187-192.
[2] CHEN L, MA B, ZHAO X H. Differential cryptanalysis of a novel image encryption algorithm based on chaos and line map[J]. Nonlinear Dynamics, 2017, 87(3): 1797-1807.
[3] 崔业勤, 丁国超. 基于单图像局部置乱和动态反馈扩散的混沌图像加密算法[J]. 电信科学, 2016, 32(11): 93-100. CUI Y Q, DING G C. Chaotic image encryption algorithm based on single image local scrambling and dynamic feedback diffusion[J]. Telecommunications Science, 2016, 32(11): 93-100.
[4] 刘会, 金聪. 基于量子混沌映射的高效安全的图像加密算法[J].计算机工程与科学, 2016, 38(11): 2227-2233. LIU H, JIN C. An efficient and secure image encryption algorithm based on quantum chaotic mapping[J]. Computer Engineering and Science, 2016, 38(11): 2227-2233.
[5] TANG Z J, WANG F, ZHANG X Q. Image encryption based on random projection partition and chaotic system[J]. Multimedia Tools and Applications, 2017, 76(7): 8257-8283.
[6] LI Y P, WANG C H, CHEN H. A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation[J]. Optics and Lasers in Engineering, 2017, 90(3): 238-246.
[7] 吴晶晶. 基于混沌置乱和Radon变换置乱的图像加密算法[D].哈尔滨: 哈尔滨工业大学, 2012.WU J J. Image encryption algorithm based on chaos system scrambling and Radon transforms scrambling[D]. Harbin: Harbin Institute of Technology, 2012.
[8] SAHA B J, KABI K K. A new approach on color image encryption using arnold 4D cat map[J]. Computational Intelligence in Data Mining, 2016, 410(37): 131-136.
[9] 郭静博, 孙琼琼. 改进的引力模型耦合明文像素相关交叉机制的图像加密算法[J]. 包装工程, 2016, 7(13): 165-172. GUO J B, SUN Q Q. Image encryption algorithm based on improved gravity model coupled with plain pixel correlation crossing mechanism[J]. Packing Engineering, 2016, 7(13): 165-172.
[10] PARVEES M Y M, SAMATH J A, BOSE B P. Protecting large size medical images with logistic map using dynamic parameters and key image[J]. International Journal of Network Security, 2017, 19(6): 984-994.
[11] LIU L F, MIAO S X. A new image encryption algorithm based on logistic chaotic map with varying parameter[J]. Springer Plus, 2016, 5(1): 1-12.
[12] 丁汀, 王晓侃. 像素交叉移位变换耦合动态和谐搜索优化机制的图像加密[J]. 华侨大学学报(自然科学版), 2017, 38(2): 229-235. DING T, WANG X K. Image encryption algorithm based on pixel cross shift transform coupling dynamic harmony search optimization mechanism[J]. Jouanal of Huaqiao University (Natural Science), 2017, 38(2): 229-235.
[13] WANG X Y, ZHANG H L. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems[J]. Nonlinear Dynamics, 2016, 83(2): 333-346.
[14] 李凯佳, 俞锐刚, 袁凌云. 基于 DNA-记忆元胞自动机与Hash函数的图像加密算法[J]. 计算机工程与设计, 2017, 38(2): 470-477. LI K J, YU R G, YUAN L Y. Image encryption algorithm based on DNA-memory element automation and Hash function[J]. Computer Engineering and Design, 2017, 38(2): 470-477.
Image encryption algorithm based on multi-direction pixel continuous folding mechanism and Radon transform
SUN Li1, HUANG Zhengqian2, XIANG Zhenmao1
1. Department of Computer and Information Technology, Zhejiang Police College, Hangzhou 310053, China 2. School of Computer Science and Technology, Zhejiang University, Hangzhou 310027, China
The image encryption algorithm based on multi-direction pixel continuous folding mechanism and Radon transform was proposed. Firstly, the initial plaintext was equally segmented to get left and right sub-blocks. Then the Radon transform was used to obtain the radon projection spectrum image by processing the left and right blocks at 0~180 degrees. And Radon projection spectrum image of left block was permutated by Arnold map, while the Radon projection spectrum image of right block was permutated based on gravity model to get two su-scrambling ciphers, then the entire scrambled image is formed by combining them. To diffuse pixels from multiple directions in space, four direction continuous folding mechanism was designed to change the pixel values by using the diffusion function corresponding to four different directions for realizing image encryption. The experimental results show that this algorithm has higher security and attack resistance with more uniform of pixel distribution in output cipher compared with the current image encryption technology.
image encryption, multi-direction pixel continuous folding, Radon transform, Radon projection spectrum, Arnold mapping, Gravity model
s: The National Natural Science Foundation of China—Zhejiang Joint Foundation for the Integration of Industrialization and Informatization (No.U1509219), Zhejiang Provincial Natural Science Foundation of China (No.LQ13F030013)
TP391
:A
10.11959/j.issn.1000-0801.2017236

孙力(1962-),男,浙江警察学院计算机与信息技术系讲师,主要研究方向为图像处理、信息安全。

黄正谦(1963-),男,浙江大学计算机科学与技术学院讲师,主要研究方向为图像处理、网络信息安全。

项振茂(1964-),男,浙江警察学院计算机与信息技术系教授,主要研究方向为信息安全、计算机取证。
2017-04-20;
:2017-06-01
国家自然科学基金——浙江省两化融合联合基金资助项目(No.U1509219);浙江省自然科学基金资助项目(No.LQ13F030013)
