基于Wishart矩阵特征值的频谱感知算法
2017-09-15杨雪梅何希徐家品
杨雪梅,何希,徐家品
(1. 四川大学锦江学院,四川 眉山 620860;2. 四川大学电子信息学院,四川 成都 610065)
基于Wishart矩阵特征值的频谱感知算法
杨雪梅1,何希2,徐家品2
(1. 四川大学锦江学院,四川 眉山 620860;2. 四川大学电子信息学院,四川 成都 610065)
为了提高频谱感知性能,克服经典算法的缺点,提出了一种新的基于Wishart随机矩阵理论的协作频谱感知算法。根据多个认知用户接收信号样本协方差矩阵特征值的对数分布特性,利用样本协方差矩阵最大特征值与几何平均特征值的比值,得到简单的判决阈值闭式表达式,实现频谱感知判决。该算法不需要知道主用户的任何先验信息,不受噪声不确定性的影响。仿真结果表明,所提算法在协作用户数少、信噪比低、采样点数极少的情况下,仍能获得较高的感知性能。该算法受虚警概率和极端值的影响较小,比同类算法有更好的检测性能。
频谱感知;Wishart随机矩阵;样本协方差矩阵;几何平均特征值;判决阈值
1 引言
在认知无线电(cognitive radio)[1]频谱感知技术中,目前最经典的频谱检测方法有匹配滤波检测(matched filtering detection,MFD)[2]、循环平稳特征检测(cyclostationary feature detection,CFD)[3]、能量检测(energy detection,ED)[4,5]3种方法。匹配滤波检测的检测精度高,但是需要知道主用户的先验信息,而循环平稳特征检测的计算量很大。相较于前两者,能量检测不需要主用户的任何先验信息,算法简单,但受噪声不确定性影响较大[6],如噪声可能是非高斯噪声[7],且对相关性信号检测性能较差。而相关性信号在多用户协作感知中常常与噪声不确定现象同时存在,随着多用户协作感知的应用愈加广泛,为了提高相关信号的检测性能,基于随机矩阵理论的多用户协作感知方法[8]成为热点。
这类方法对独立同分布信号和相关信号均适用,克服了经典感知方法的一些缺点,但也存在各自的优缺点。参考文献[9]中采用 DSCM(determinant of sample covariance matrix)算法,该算法不敏感于协作用户数,但要在满足大采样点数、高信噪比的条件下,其检测性能才好;参考文献[10]中提出了两种基于算术平均特征值的感知算法,其中,AME(average to maximum eigenvalue)算法采用算术平均特征值与最大特征值的比值作为判决统计量,在大样本情况下,受虚警概率的影响较大,而另一种AMME(average to maximum-minimum eigenvalue)算法采用算术平均特征值与最大最小特征值之差的比值为判决统计量[11];同时,基于随机矩阵最大最小特征值方面的研究越来越多,如参考文献[12,13]中分别提出的NMME(novel maximum-minimum eigenvalue)算法和LED(least eigenvalue distribution)算法,这两种算法的检测性能都比较高,LED算法的检测性能略高于NMME算法,但它们分别依赖于一阶和二阶Tracy-Widom分布函数,而这两种分布函数都没有具体的闭式表达式。
为了提高频谱感知能力,在小采样点数、低信噪比条件下获得较高的检测性能,本文在Wishart随机矩阵理论的基础上,提出了一种基于随机矩阵特征值分布的频谱感知算法,利用样本协方差矩阵特征值的对数分布形式,以随机矩阵样本协方差矩阵最大特征值与几何平均特征值(maximum-geometric mean eigenvalue,MGME)比值[14]为判决门限统计量,对频谱检测做出判决。
2 系统模型
认知用户的信号检测可以用一个二元假设检验模型[6,15]表示:

其中,H0表示没有主用户信号存在,只有噪声的情况;H1表示主用户信号和噪声都存在的情况。xi( k)表示第i个认知用户在k( k=1,2,…,N)时刻采样到的信号;hi( k)表示信道增益;ni( k)表示高斯白噪声,其均值为0、方差为;si( k)表示主用户信号。
用向量形式H、X以及n分别将信道增益、接收信号以及噪声表示成如下形式:

则接收信号可以进一步用M×N维矩阵表示:

根据以上的定义,式(1)能够被表示为:

假设噪声n是独立同分布信号,且信号S与噪声n不相关,则在样本数N足够大的情况下,接收信号样本协方差矩阵Rx(N)可定义为:

其中,样本协方差矩阵Rx(N)的行列式即样本协方差矩阵所有特征值的乘积,可记为:

其中,λi表示矩阵Rx(N)的第i个特征值。用λmax、λmin表示矩阵Rx(N)的最大特征值和最小特征值。
3 MGME算法的理论分析
3.1 算法的理论基础
当主用户信号不存在(H0)时,Rx(N)是一个特殊的Wishart矩阵[16],可记为:

其中, IM为M×M维的单位矩阵。



当采样点数N远大于协作用户数M时:
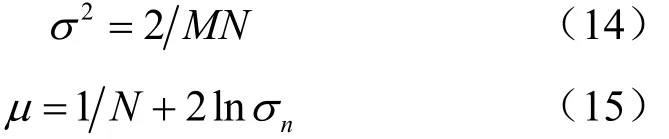
3.2 算法的阈值推导
基于以上的理论分析,本文将几何平均特征值与最大特征值之比作为判决统计量:

在预先给定虚警概率 Pfa作为已知量的条件下,建立判决阈值与虚警概率之间的关系,用标准Q函数表示为:

因此,判决阈值可以表示为:

由式(18)可知,判决阈值γ只与虚警概率、协作用户数以及采样点数有关,与噪声无关,不受噪声不确定性的影响。
3.3 算法判决阈值的有效性
图1给出了MGME算法的判决阈值γ、信号与噪声同时存在情况下以及只有噪声情况下的仿真比值随采样点数变化的关系曲线,其中,协作用户数 M=10,虚警概率Pfa=0.01,信噪比SNR=-10 dB。由理论分析可知:γ随采样点数的变化而动态调整;在相同采样点数情况下,信号与噪声同时存在情况下的仿真比值应当大于γ,而只有噪声情况下的仿真比值应当小于γ;此外,由于虚警概率的存在,在只有噪声情况下的仿真比值曲线上,也可能存在极少的点位于γ关系曲线的上方。由图1可知,MGME算法的判决阈值是有效的。

图1 MGME判决阈值的有效性
4 算法性能仿真
4.1 仿真环境及工具
为了验证所提MGME算法的检测性能,本文将从两方面对MGME算法进行仿真分析:从不同采样点数、协作用户数、信噪比以及不同虚警概率情况下对MGME算法进行仿真分析;将所提算法与LED、AMME以及AME等同类算法作比较。实验采用10 000次的Monte Carlo(蒙特卡洛)仿真,仿真平台为MATLAB(R2013a)。
4.2 采样点数、协作用户数以及信噪比对检测性能的影响
为了更好地分析,表1列出了在不同采样点数M、协作用户数N以及信噪比SNR下,MGME算法的检测概率 Pd,由表1可知,仿真选取较少的采样点数,在低协作用户数和低信噪比条件下,也能获得较高的检测概率。

表1 不同情况下的检测概率
图2为Pfa=0.05,分别取协作用户数M=5、10,采样点数N=100、200、500时,检测概率随信噪比变化的关系曲线。

图2 不同M、N下的信噪比与检测概率的关系曲线
4.3 虚警概率对检测性能的影响
图3为M=10,分别取采样点数 N=100、200、350,信噪比SNR=-10 dB 、 -15dB时,检测概率随虚警概率变化的关系曲线。仿真结果表明,当虚警概率从 0.01增加到 0.1的过程中,在不同的采样点数和信噪比情况下,MGME算法的检测概率增加均不到 0.15,由此可知,MGME算法受虚警概率的影响较小;此外,仿真选取较低的采样点数和信噪比,当采样点数N=200,信噪比SNR=-10 dB时,MGME算法的检测概率为1。在实际情况中,可根据信噪比的高低选择合适的采样点数,以达到最优的检测性能。

图3 不同N、SNR下的检测概率与虚警概率之间的关系
4.4 MGME算法与其他同类算法的性能比较
这部分将MGME算法与LED、AMME、AME以及DSCM算法从几个不同方面进行仿真分析与比较。

图4 检测概率与采样点数之间的关系
图 5表示各种算法在不同信噪比情况下的检测性能,N=200, Pfa=0.05,M=20。从图 5可以看出,AME和AMME两种算法的关系曲线几乎是重合的,MGME算法的关系曲线明显高于其他4种算法。当信噪比SNR=-14 dB 时,DSCM算法的检测概率只有0.278,LED算法为0.903,AMME算法为0.923,AME算法为0.934,MGME算法已达0.954,由图5可知,在低信噪比情况下,MGME算法的检测性能是最好的。

图5 检测概率与信噪比之间的关系
为了更好地分析,表2列出了当N=100时,各种算法在是否存在极端值两种情况下检测概率的偏差(取正值),由表2可知,在N=100时,MGME算法的偏差最小,AME算法略高于MGME算法,其他3种算法检测概率的偏差远大于MGME、AME两种算法。

表2 N=100时是否存在极端值两种情况下各算法检测概率的偏差
图6表示在是否存在极端值两种情况下,各种算法的检测概率随采样点数变化的关系曲线,其中。此外,从图6中可以看到,DSCM、LED和AMME 3种算法在存在极端值情况下的关系曲线与理想情况下相差甚远,MGME和AME两种算法在存在极端值情况(无极端值)下的关系曲线与理想情况下只有较小的差异,而MGME算法在采样点数达到130时,是否有极端值两种情况下的关系曲线已几乎重合,此时 AME算法仍然保持大约 0.02的偏差。综上所述,5种算法中,只有 AME和MGME两种算法受极端值的影响较小,而MGME算法受极端值的影响是最小的。
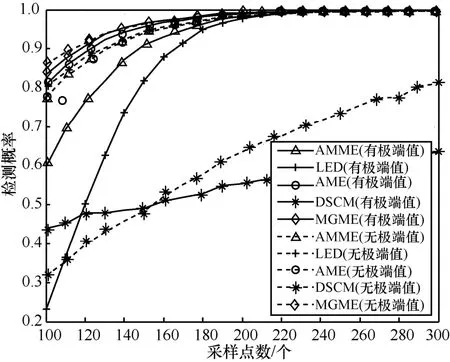
图6 检测概率与采样点数之间的关系
由上述仿真结果可知,所提MGME算法受虚警概率和极端值的影响较小,在低协作用户数和低信噪比条件下,也能通过极少的采样点数,获得较高的检测概率;此外,与AMME、AME和LED等基于特征值的同类算法相比,在不同信噪比、采样点数以及协作用户数情况下,MGME算法表现出了更好的检测性能。
5 结束语
本文运用Wishart随机矩阵特征值的对数分布特性,提出了一种基于样本协方差矩阵最大特征值与几何平均特征值比值的算法,即MGME算法。该算法不依赖于Tracy-Widom分布函数,且能得到一个判决阈值闭式表达式,当虚警概率、协作用户数、采样点数等参数确定后,判决阈值能够获得物理意义明确的检测结果。另外,由于判决阈值只与虚警概率、协作用户数、采样点数有关,因此在主用户信息动态变化时,算法性能也很稳定。通过仿真可知,该算法克服了噪声不确定性对检测性能的不利影响,在采样点数、协作用户数以及信噪比均较小的情况下,能获得较高的检测性能,算法简单,复杂度不高,并且受虚警概率和极端值的影响较小,与同类算法相比,所提算法能获得更好的检测性能。
[1] 毕志明, 匡镜明, 王华. 认知无线电技术的研究及发展[J].电信科学, 2006, 22(7): 57-60. BI Z M, KUANG J M, WANG H. Research status and development trend of cognitive radio[J]. Telecommunications Science, 2006, 22(7): 57-60.
[2] CABRIC D, MISHRA S M, BRODERSEN R W. Implementation issues in spectrum sensing for cognitive radios[C]//The Thirty-Eighth Asilomar Conference on Signals, System and Computers, Nov 7-10, 2004, Pacific Grove, CA, USA. New Jersey: IEEE Press, 2004: 772-776.
[3] SUTTON P D, NOLAN K E, DOYLE L E. Cyclostationary signatures in practical cognitive radio applications[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(1): 13-24.
[4] URKOWITZ H. Energy detection of unknown detenninistic signals[J]. Proceedings of the IEEE, 1967, 55(4): 523-531.
[5] 付彩梅, 李有明, 周桂莉, 等. 一种基于能量检测的协作式频谱感知算法[J]. 电信科学, 2016, 22(9): 52-60. FU C M, LI Y M, ZHOU G L, et al. A new cooperation spectrum sensing algorithm based on energy detection[J]. Telecommunications Science, 2016, 22(9): 52-60.
[6] SAHAI A, HOVEN N, TANDRA R. Some fundamental limits on cognitive radio[C]//The Forty-First Annual Allerton Conference on Communication, Control and Computing, Sept 29-Ooc 1, 2004, Monticello, VA, USA. [S.l.:s.n.], 2004: 1-10.
[7] 何智勇. 认知无线电中一种改进的 AVC 频谱感知算法[J].电信科学, 2017, 33(2): 98-103. HE Z Y. Modified absolute value cumulating spectrum sensing algorithm in cognitive radio[J]. Telecommunications Science, 2017, 33(2): 98-103.
[8] TULINO A M, VERDU S. Random matrix theory and wireless communication[M]. Boston-Delft: Now Publisher Inc, 2004.
[9] LEI K J, YANG X, PENG S L, et al. Determinant of the samplecovariance matrix based spectrum sensing algorithm for cognitive radio[C]//Seventh International Conference on Wireless Communications, Networking and Mobile Computing(WiCOM), Sept 23-25, 2011, Wuhan, China. New Jersey: IEEE Press, 2011: 1-4.
[10] 徐家品, 杨智. 基于随机矩阵特征值比的频谱感知改进算法[J].电波科学学报, 2015(2): 282-288. XU J P, YANG Z. Improved spectrum sensing algorithms based on eigenvalue ratio of random matrix[J]. Chinese Journal of Radio Science, 2015(2): 282-288.
[11] PILLAY N, XU H J. Blind eigenvalue-based spectrum sensing for cognitive radio networks[J]. IET Communications, 2012, 6(11): 1388-1396.
[12] 弥寅, 卢光跃. 基于特征值极限分布的合作频谱感知算法[J].通信学报, 2015, 36(1): 84-89. MI Y, LU G Y. Cooperative spectrum sensing algorithm based on limiting eigenvalue distribution[J]. Journal on Communication, 2015, 36(1): 84-89.
[13] 杨智, 徐家品. 基于最小特征值分布的频谱感知算法[J]. 计算机应用, 2015, 35(2): 354-357. YANG Z, XU J P. Spectrum sensing algorithm based on least eigenvalue distribution[J]. Journal of Computer Applications, 2015, 35(2): 354-357.
[14] 何希, 杨雪梅, 徐家品. 基于随机矩阵最大特征值分布的频谱感知算法[J]. 计算机测量与控制, 2017, 25(2): 123-129. HE X, YANG X M, XU J P. Spectrum sensing algorithm based on maximum eigenvalue distribution of random matrix[J]. Computer Measurement and Control, 2017, 25(2): 123-129.
[15] NGUYEN-THANH N, KOO I. Evidence-theory-based cooperative spectrum sensing with efficient quantization method in cognitive radio[J]. IEEE Transactions on Vehicular Technology, 2011, 60(1): 185- 195.
[16] BAO Z Q, HUANG Q D, ZHAI Y Z, et al. Fast blind spectrum sensing method based on determinant of covariance matrix[C]//2012 International Conference on Computer Science and Information Processing, Aug 24-26, 2012, Xi’an, China. New Jersey: IEEE Press, 2012: 439-443.
[17] MUIRHEAD B J. Aspects of multivariate statistical theory[M]. New Jersey: John Wiley&Sons, 1982.
Spectrum sensing algorithm based on the eigenvalue of Wishart random matrix
YANG Xuemei1, HE Xi2, XU Jiapin2
1. College of Jinjiang, Sichuan University, Meishan 620860, China 2. College of Electronics and Information Engineering, Sichuan University, Chengdu 610065, China
In order to improve the spectrum sensing performance and overcome the shortcomings of the classical algorithm, a new cooperative spectrum sensing algorithm based on Wishart random matrix theory was proposed. According to the logarithmic distribution characteristics of the sampled covariance matrix eigenvalues and using the ratio of maximum eigenvalue and geometric mean eigenvalue, a simple closed-form threshold expression could be obtained, and the spectrum sensing decision could be performed depend on the threshold. The simulation results show that the proposed algorithm can get better sensing performance even under the conditions of a few number of cooperative users, low signal to noise ratio and a few samples. It is less affected by false-alarm probability and the extreme values, and has better detection performance than similar algorithms.
spectrum sensing, Wishart random matrix, sample covariance matrix, geometric mean eigenvalue, threshold expression
TN925
:A
10.11959/j.issn.1000-0801.2017255

杨雪梅(1983-),女,四川大学锦江学院讲师,四川省通信学会会员,主要研究方向为通信与信息系统、多媒体通信等。

何希(1991-),女,四川大学电子信息学院硕士生,主要研究方向为通信与信息系统。

徐家品(1957-),男,四川大学电子信息学院教授,主要研究方向为通信与信息系统。
2017-06-26;
:2017-08-28
