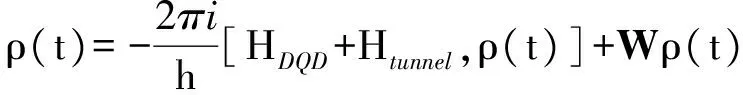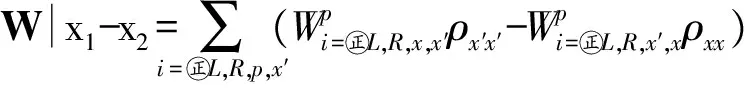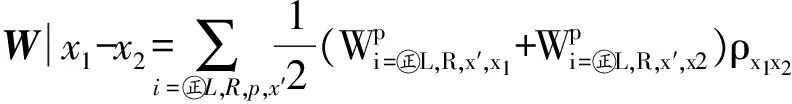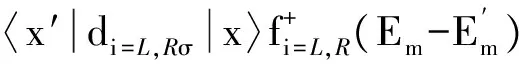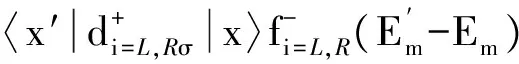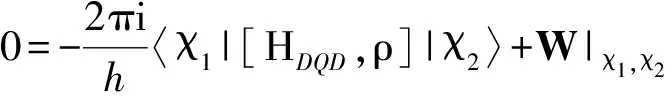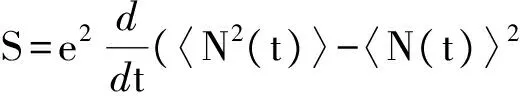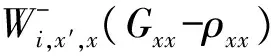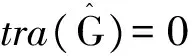马约拉纳费米子-量子点杂化系统输运性质的研究

毛 祥, 吴绍全

(四川师范大学 物理与电子工程学院， 四川 成都 610101)

马约拉纳费米子-量子点杂化系统输运性质的研究

毛 祥, 吴绍全*

(四川师范大学 物理与电子工程学院， 四川 成都 610101)

从理论上研究马约拉纳费米子-量子点杂化系统的输运性质.基于广义主方程方法,计算通过此系统的电流、微分电导和Fano因子.计算结果表明:马约拉纳费米子与量子点中电子的耦合导致系统的零偏置反常,而2个马约拉纳费米子的耦合压制系统的零偏置反常.

马约拉纳费米子； 零偏置反常； 主方程方法； 微分电导； Fano因子

在最近几年，针对拓扑超导体的研究已经成为凝聚态物理中非常热门的课题[1-4],其主要原因之一是理论研究表明拓扑超导体中的含有马约拉纳费米子.马约拉纳费米子满足非阿贝尔交换统计[5-9],其主要特征就是它的反粒子是它自己本身,即如果γ为马约拉纳费米子的消灭算子,则有γ=γ+,这使得该粒子不受退相干的影响,这在拓扑量子计算机中有重要的潜在应用价值[10-11].此外,在分数量子霍尔系统、P-波超导体半量子涡旋、掺杂拓扑绝缘体中超导涡旋的两端等都存在马约拉纳费米子.目前,大量的理论研究已经提出了如何在实验室中实现拓扑超导体[12-23],许多探测马约拉纳费米子的仪器已在实验室中制造出来了,并已初步探测到了马约拉纳费米子存在的信息[24-32].在这些信息中,最为引人关注的一个实验探测是把一根半导体量子线与一个超导体接触,由于近邻效应,这根半导体量子线带有超导性；再把它与一根金属线组成一个杂化系统,在这个系统中探测到了一个电导的零偏置常峰作为马约拉纳费米子存在的证据[24-26].

拓扑量子计算机的主要优点是不受退相干的影响,且计算的基础是由成对的马约拉纳费米子构成.每对马约拉纳费米子在空间中都是分离的,每个马约拉纳费米子只与另一个马约拉纳费米子耦合成对,由此形成一个费米能级，能级的占据数可以编码为一个量子比特，这种非局域的拓扑量子比特不受局域的微扰的影响.然而基于同样的原因，要转移和读出拓扑态的信息同样是一个大的挑战.现在已经有人建议用马约拉纳费米子-量子点杂化系统作为解决这个问题的途径之一[33].各种不同的马约拉纳费米子-量子点杂化系统[26-33]被提出来的目的是探测马约拉纳费米子、调整非局域关联、估计寿命、消除无序的影响.因此，研究马约拉纳费米子-量子点杂化系统的输运性质是重要的.

本文基于广义主方程方法研究了马约拉纳费米子-量子点杂化系统的输运性质，研究结果表明：马约拉纳费米子与量子点中电子的耦合Tm消除了系统的四重简并，但维持了系统4个双重简并，而双重简并的基态随偏压的增加而负增长，由此导致系统的零偏置反常；库仑相互作用仅仅增加了系统量子态|e4〉和|o4〉的能量,因而增加了电流台阶,但库仑相互作用不会改变系统量子态的简并度,也不会压制零偏置反常现象.而2个马约拉纳费米子的耦合压制了系统的零偏置反常,并消除了基态和最高能态的双重简并，但维持了2个中间能态的简并.

本文所研究的系统(系统模型如图1)可用一个与马约拉纳费米子相耦合的单量子点安德森模型描述[33-34].哈密顿量H=Hlead+HQD+Htunnel,3个分量分别为:

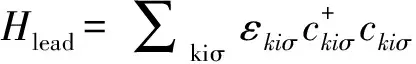
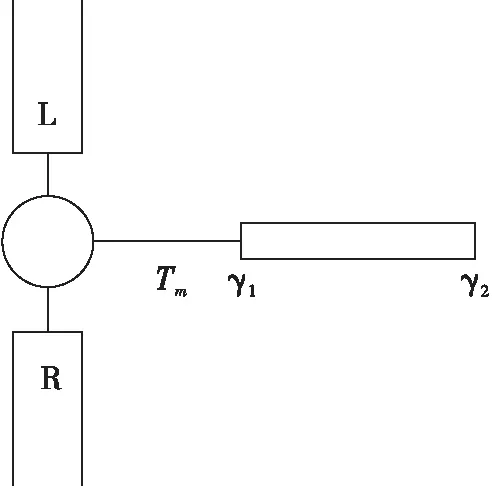
图 1 系统模型

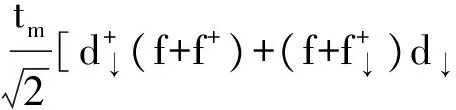
Htunnel是导体与量子点之间的隧穿耦合，其耦合强度可以用其固有线性宽度来表示，用公式可表示成Γiσ=2π|ti|2ρiσ,，ti指的是量子点与左右两端导体的隧穿矩阵元，而ρiσ指的是对应导体中的电子态密度.

在主方程近似下,与马约拉纳费米子耦合的单量子点系统共有8个量子态，分别为：|0,0〉、|↑,0〉、|↓,0〉、|0,1〉、|↑,1〉、|↓,1〉、|↑↓,0〉、|↑↓,1〉；但这8个量子态不是HQD的本征态,通过久期方程,可以得到该哈密顿量的本征值和本征能量如表1所示.

表 1 系统本征态和能量

表1中各式的参数为：

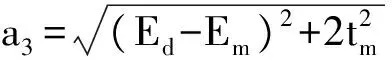
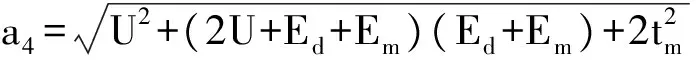
b1=-(Ed+Em+a1)， b2=-(Ed+Em-a1)，

b3=-(Ed-Em+U+a2)， b4=-(Ed-Em+U-a2)，

b5=-(Em-Ed+a3)， b6=-(Em-Ed-a3)，

b7=-(Ed+Em+U+a4)， b8=-(Ed+Em+U-a4)，

Ee1=(Ed-a1)/2, Ee2=(Ed+a1)/2,

Ee3=(3Ed+U-a2)/2, Ee4=(3Ed+U+a2)/2,

Eo1=(Ed-a3)/2, Eo2=(Ed+a3)/2,

Eo3=(3Ed+U-a4)/2, Eo4=(3Ed+U+a4)/2.

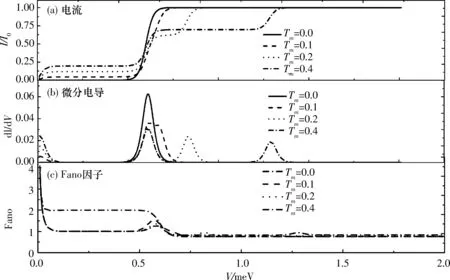
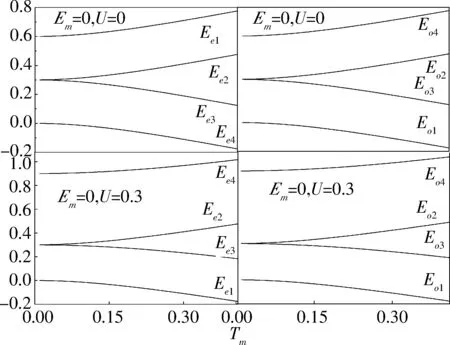
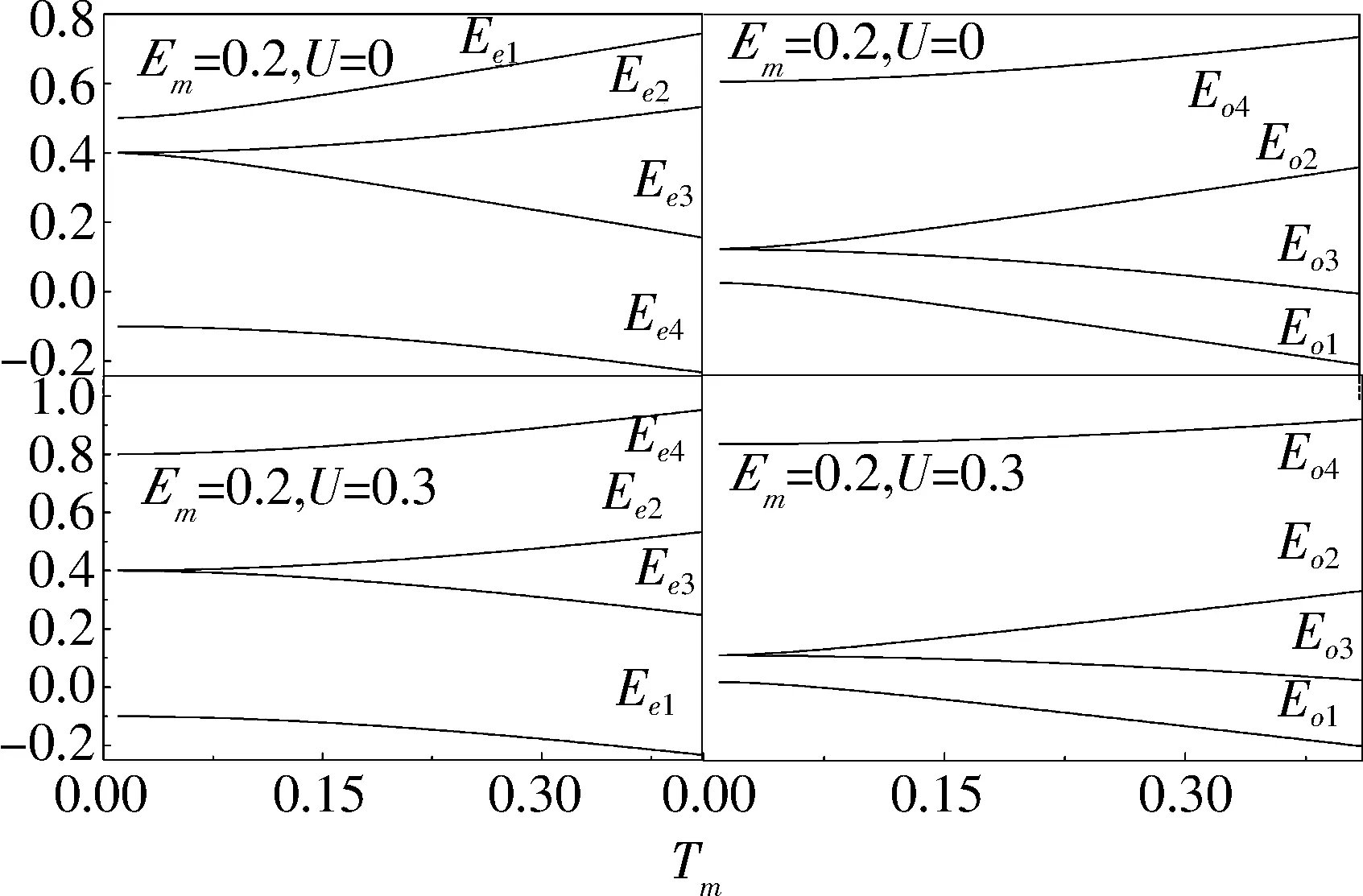
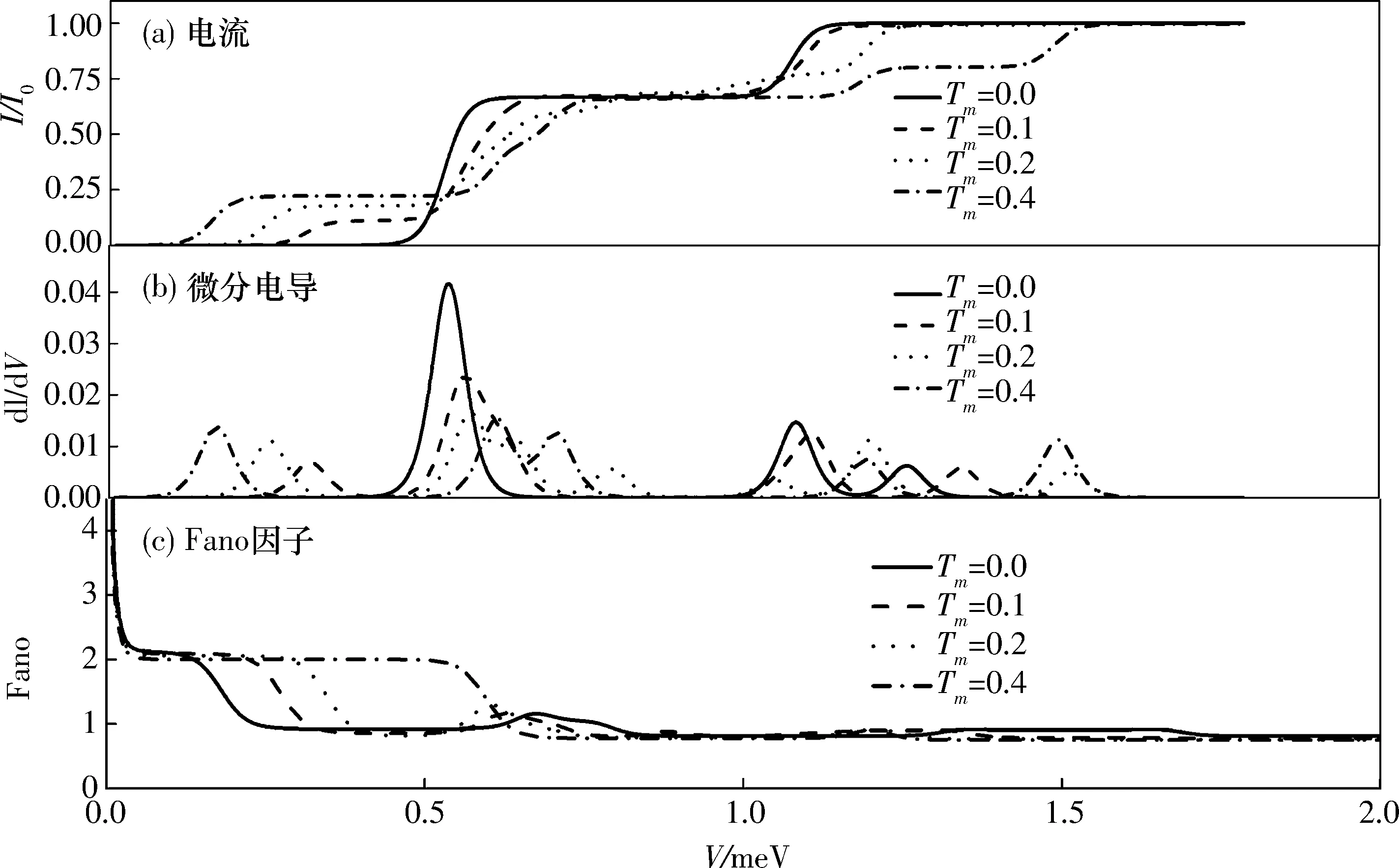
本文主要研究量子点与电极处于弱耦合时的输运性质，选择Γiσ

(2)

其中W是一个矩阵,与隧穿进程相关.约化密度算子在系统量子态中的矩阵元ρx1x2=〈x1|ρ|x2〉,其中x1和x2是双量子点系统的本征态.当x1=x2=x时,密度矩阵的对角元ρx1x2代表了双量子点系统处于x态的概率,所表征的意思是在量子点系统中可以探测到量子态x出现的几率的大小.

(3a)

在方程3(a)和3(b)中,p=+、-描述了在电子跃迁时电子的流向,+表示电子流向为流入量子点,-表示电子流向为流出量子点.当量子态通过正交化处理后,矩阵W只包含对角元,

(4a)

在定态的情况下,系统各个占有态出现的几率是稳定的,满足一般主方程

(5)

通过使用归一化条件,求解8个方程组成的线性齐次方程组,可得到约化密度矩阵的各个矩阵元.将约化密度矩阵元素代入(6)式便可得到通过系统的电流

(6)其微分电导由di=dIi/dU计算.此外，电流实际上是由大量单个电子单独作用的总结果,而每个电子

可以认为是随机独立出现的,所以电子形成的电流并不是固定不变的，而是在一个平均值上起伏变化，散粒噪声就是反映电流这种起伏变化大小的量，因此散粒噪声可以为提供电流所不能提供的有关电子输运的额外信息.计算散粒噪声[36]的标准公式为

(7)

在主方程近似下，零频散粒噪声[32-33]的计算公式可表示为

(8)

ρxx〈x′|-Ii|x〉ρx′x′〈x|]=0.

(9)

计算中一些具体参数取值：T=0.01,ΓL=ΓR=Γ0=0.005,Ed=0.3,和I0=2πeΓ0/h,所有参数都以Γ0作为能量单位.

首先讨论Em=0,U=0的情况,图2展示了通过量子点的电流、微分电导和Fano因子随偏压变化的情况，而图3展示了量子态能量随Tm变化的情况.

图 2 在Em=0和U=0时，通过系统的电流、微分电导和Fano因子随电压的变化曲线

图 3 系统各量子态的能量随Tm变化的曲线

当Tm=0的时候，从图2中可以发现，在U<2Ed时，由于偏压没有达到阈值电压，量子点是空的和电流被阻塞.随着偏压的增加接近阈值电压时，系统的量子态开始由态|e1〉和|o1〉向态|e2〉、|e3〉、|e4〉、|o2〉、|o3〉和|o4〉跃迁，使得通过系统的序贯电流开始单调地增加，并最终到达一个平台,并在U=2Ed=0.6 V处,其微分电导的变化曲线上出现的一个波峰.在U<2Ed时，Fano因子大于1，这种超泊松噪声的现象是由于偏压小于阈值电压，电子的隧穿受到压制所致;当U

涨落导致Fano因子开始趋于发散;而在U>2Ed时，Fano因子小于1(泊松噪声)但大于0.5(双势垒噪声).从图3的能级图可以看到，此时量子态|e1〉与|o1〉和量子态|o3〉与|o4〉为二重简并,而|e2〉、|e3〉、|o2〉和|o3〉为四重简并.当Tm≠0时,情况起了变化,原来四重简并的量子态|e2〉、|e3〉、|o2〉和|o3〉分裂成了|e2〉与|o2〉和|e3〉与|o3〉的二重简并,Ee2和Eo2与Ee4和Eo4一样，其值随Tm的增加而增加;但Ee3和Eo3随Tm的增加而减少，这导致电流线型呈现出多台阶.尤其值得注意的是，Ee1和Eo1随Tm的增加而负增长，这导致在偏压为零时电子隧穿就开始出现了，这就是著名的零偏置反常现象.微分电导在电流线型中每个台阶处都出现了一个波峰，而Fano因子在U<2Ed时等于1，为泊松噪声，并在U=0.6 V处出现了一个峰值大于1的波峰，这是由于在偏压达到阈值电压时打开了一个新的电子隧穿通道,导致电流有大的涨落.从图3还可以看到，随着偏压的增加，每打开一个电子隧穿通道都会导致Fano因子出现一个波峰.在Tm的增加过程中,整个系统保持偶宇称量子态与奇宇称量子态一对一的双重简并,既Tm的出现消除了系统的四重简并,但保持了系统的双重简并,导致零偏置反常现象的出现.

图 4 在Em=0和U=0.3 V时，通过系统的电流、微分电导和Fano因子随电压的变化曲线

图4展示了当Em=0,U=0.3 V时通过量子点的电流、微分电导和Fano因子随偏压变化的情况.可以看到,在Tm=0时,库仑相互作用增加了量子态|e4〉和|o4〉的能量,也就增加了量子点通过这2个量子态隧穿的阈值电压,导致电流线型呈现出2个台阶,分别对应2个阈值电压U=0.6和1.2 V,伴随每个电流台阶的出现都会在微分电导和Fano因子线型中留下一个波峰,标志着电子隧穿通道的打开所引起电流的涨落.与图2一样,随着Tm的出现,不仅导致零偏置反常现象,也使四重简并量子态|e2〉、|e3〉、|o2〉和|o3〉的退化为二重简并,使得电流线型最后呈现出4个台阶,伴随电流线型中每个台阶处的出现都会导致在微分电导和Fano因子线型中出现一个波峰,所以库仑相互作用仅仅增加了量子态|e4〉和|o4〉的能量,因而增加了电流台阶,但库仑相互作用不会影响系统量子态的简并度,也不会压制零偏置反常现象.

图 5 在Em=0.2和U=0时，通过系统的电流、微分电导和Fano因子随电压的变化曲线

在Em=0.2,U=0时,图5展示了通过量子点的电流、微分电导及Fano因子随偏压变化的情况，而图6展示了量子态能量随Tm变化的情况.从图5中可以看到:原来二重简并的量子态|e1〉与|o1〉和|o3〉与|o4〉分裂了,而原来四重简并的量子态|e2〉、|e3〉、|o2〉和|o3〉分裂为|e2〉与|e3〉和|o2〉与|o3〉的二重简并,如此系统形成了4个激发态.特别是分裂后的量子态|e1〉的能量小于零,而量子态|o1〉的能量大于零,Em导致系统量子态能级的这种分裂显著地改变了系统的输运性质.首先讨论Tm=0的情况.从图6中可以清楚地看到:电流、微分电导和Fano因子随偏压变化的情况与Em=0和U=0时的情况是一样的,这说明单独Em的出

图 6 系统各量子态的能量随Tm变化的曲线

Fig. 6 The eigenenergies of quantum states of the system as a function ofTm

现不会影响量子点的输运性质.这很好理解,因为这时量子点与P-波超导体退藕.然而当Tm≠0的时候情况有了很大地不同.随Tm的增加,由于Em消除了系统的能级简并,形成了4个激发态,出现了4个阈值电压,控制着4个电子隧穿通道,随着偏压的增加,4个电子隧穿通道依次被打开,最后导致电流线型随偏压的变化出现了4个台阶,每个台阶的出现都会在微分电导和Fano因子的线型中留下一个波峰.特别是由于Em消除了基态能级Ee1和Eo1的简并,并且Ee1<0而Eo1>0,这导致零偏置反常消失了.此外在偏压小于阈值电压的阻塞区,Fano因子大于1,系统出现由于电子隧穿受到阻塞而导致的超泊松噪声现象,一旦打开一个电子隧穿通道,Fano因子迅速降为一,系统进入泊松噪声.这点与Em=0似的情况不一样,在那里由于Tm≠0时系统出现零偏置反常,所以一旦Tm≠0,Fano因子迅速降为一,系统进入泊松噪声.

图7展示了在Em=0.2,U=0.3 V时,通过量子点的电流、微分电导及Fano因子随偏压变化的情况，此时的情况与Em=0.2,U=0时稍有不同的是在Tm=0时,由于库仑相互作用的出现,增加了双占据态的能量,导致电流线型随偏压的变化出现了2个台阶.但随着Tm的增加,其能级分裂情况与在Em=0.2,U=0时能级分裂情况是一样的,电流线型随偏压的变化最后演变出了4个台阶,而微分电导和Fano因子随偏压变化的线型在2种取值条件下也是一样的,这说明当Em和Tm都不为零时,库仑相互作用U对量子点输运性质没有影响.

图 7 在Em=0.2和U=0.3 V时，通过系统的电流、微分电导和Fano因子随电压的变化曲线

本文研究了马约拉纳费米子-量子点杂化系统的输运性质，研究结果表明:马约拉纳费米子与量子点中电子的耦合Tm导致了系统的零偏置反常，并消除了系统的四重简并,使系统变成了4个双重简并.库仑相互作用仅仅增加了系统量子态|e4〉和|o4〉的能量,因而增加了电流台阶,但库仑相互作用不会改变系统量子态的简并度,也不会压制零偏置反常现象.而2个马约拉纳费米子的耦合压制了系统的零偏置反常,并消除了基态和最高能态的双重简并，但维持了2个中间能态的简并.该系统的这些性质在量子器件开发和拓扑量子计算开发等方面有重要的意义.

[1] EUGENIE S R. A solid case for Majorana fermions[J]. Nature,2012,483(7388):132.

[2] BROUWER P W. Enter the Majorana fermion[J]. Science,2012,336(6084):989-990.

[3] WILCZEK F. Quantum physics:Majorana modes materialize[J]. Nature,2012,486(7402):195-197.

[4] ALICEA J. New directions in the pursuit of Majorana fermions in solid state systems[J]. Reports on Progress in Physics Physical Society,2012,75(7):076501.

[5] 郭雪林,黄劲松,谢征微,等. FM/I/FM隧道结中的隧穿时间[J]. 四川师范大学学报(自然科学版),2009,32(2):202-205.

[6] READ M N. Nonabelions in the fractional quantum Hall effect[J]. Nuclear Physics,1991,B360(2/3):362-396.

[7] NAYAK C, WILCZEK F. 2n-quasihole states realize 2n-1-dimensional spinor braiding statistics in paired quantum Hall states[J].Nuclear Physics,1996,B479(3):529-553.

[8] 陈尚荣,徐明,刘杰. 铁磁体/有机体/铁磁体三明治结构的隧穿磁电阻[J] . 四川师范大学学报(自然科学版),2009,32(4):482-485.

[9] READ N, GREEN D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect[J]. Phys Rev,2000,B61:10267.

[10] KITAEV A Y. Fault-tolerant quantum computation by anyons[J]. Ann Phys,2003,303(1):2-30.

[11] NAYAK C, SIMON S H, Stern A, et al. Non-Abelian anyons and topological quantum computation[J]. Rev Mod Phys,2008,80:1083.

[12] FU L, KANE C L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator[J]. Phys Rev Lett,2008,100(9):096407.

[13] 侯涛,吴绍全,毕爱华. 耦合于铁磁电极平行双量子点的自旋极化输运[J]. 四川师范大学学报(自然科学版),2009,32(2):210-214.

[14] FU L, KANE C L. Josephson current and noise at a superconductor/quantum-spin-Hall-insulator/superconductor junction[J]. Phys Rev,2009,B79:161408.

[15] SAU J D, LUTCHYN R M, TEWARI S, et al. Generic new platform for topological quantum computation using semiconductor heterostructures[J]. Phys Rev Lett,2010,104(4):040502.

[16] ALICEA J. Majorana fermions in a tunable semiconductor device[J]. Phys Rev,2010,B81:125318.

[17] 李玲,高洁. 单电子输运器件及其研究进展[J]. 四川师范大学学报(自然科学版),2009,32(6):822-833.

[18] LUTCHYN R M, SAU J D, SARMA S D. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures[J]. Phys Rev Lett,2010,105(7):077001.

[19] OREG Y, REFAEL G, VON OPPEN F. Helical liquids and Majorana bound states in quantum wires[J]. Phys Rev Lett,2010,105(17):177002.

[20] COOK A, FRANZ M. Majorana fermions in a topological-insulator nanowire proximity-coupled to an s-wave superconductor[J]. Phys Rev,2011,B84:201105.

[21] 徐明,魏屹,何贤模,等. Si/SiNx多层膜能带结构的理论研究[J]. 四川师范大学学报(自然科学版),2010,33(4):545-548.

[22] SAU J D, SARMA S D. Realizing a robust practical Majorana chain in a quantum-dot-superconductor linear array[J]. Nature Commun,2012,3(1):964.

[23] NADJPERGE S, DROZDOV I K, BERNEVIG B A, et al. Proposal for realizing Majorana fermions in chains of magnetic atoms on a superconductor[J]. Phys Rev,2013,B88:020407.

[24] MOURIK V, ZUO K, FROLOV S M, et al. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices[J]. Science,2012,336 (6084):1003.

[25] DAS A, RONEN Y, MOST Y, et al. Zero-bias peaks and splitting in an Al-InAs nanowire topological superconductor as a signature of Majorana fermions[J]. Nature Phys,2012,8(12):887-895.

[26] DENG M T, YU C L, HUANG G Y, et al. Anomalous zero-bias conductance peak in a Nb-InSb nanowire-Nb hybrid device[J]. Nano Lett,2012,12(12):6414-6419.

[27] FINCK A D K, VAN HARLINGEN D J, MOHSENI P K, et al. Anomalous modulation of a zero-bias peak in a hybrid nanowire-superconductor device[J]. Phys Rev Lett,2013,110:126406.

[28] CHURCHILL H O H, FATEMI V, GROVE-RASMUSSEN K, et al. Superconductor-nanowire devices from tunneling to the multichannel regime:Zero-bias oscillations and magnetoconductance crossover[J]. Phys Rev,2013,B87:241401.

[29] NADJPERGE S, DROZDOV I K, LI J, et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor[J]. Science,2014,346(6209):602-607.

[30] DENG M T, YU C L, HUANG G Y, et al. Parity independence of the zero-bias conductance peak in a nanowire based topological superconductor-quantum dot hybrid device[J]. Sci Rep,2013,4(7621):7261-7261.

[31] HIGGINBOTHAM A P, ALBRECHT S M, KIRSANSKAS G, et al. Parity lifetime of bound states in a proximitized semiconductor nanowire[J]. Nature Phys,2015,11(12):1017-1021.

[32] ALBRECHT S M, HIGGINBOTHAM A P, MADSEN M, et al. Exponential protection of zero modes in Majorana islands[J]. Nature,2016,531(7593):206-209.

[33] LEIJNSE M, FLENSBERG K. Quantum information transfer between topological and spin qubit systems[J]. Phys Rev Lett,2011,107(21):210502.

[34] LEE M, LIM J S, LPEZ R. Kondo effect in a quantum dot side-coupled to a topological superconductor[J]. Phys Rev,2013,B87:241402.

[35] BLUM K. Density Matrix Theory and Applications[M]. New York:Taylor & Francis,1996.

[36] BLANTER Y M, BÜTTIKER M. Shot noise in mesoscopic conductors[J]. Physics Reports,2000,336(1/2):1-166.

(编辑 余 毅)

The Study of the Transport Properties of the Majorana Fermion-quantum Dot Hybrid System

MAO Xiang WU Shaoquan

(CollegeofPhysicsandElectronicEngineering,SichuanNormalUniversity,Chengdu610101,Sichuan)

We theoretically investigate the effect of the Majorana fermion on the transport properties through quantum dot hybrid system. With the framework of the generalized master equation method, we analyze the current through system, differential conductance and Fano factor as a function of bias. Our results reveal that the coupling of the Majorana fermion and electrons on the quantum dot can lead to a zero-bias anomaly, while the coupling of the two Majorana fermion inhibits the zero-bias anomaly, and relevant underlying physics problems is discussed.

the Majorana fermion; zero-bias anomaly; master equation method; differential conductance; Fano factor

2016-10-16

四川省教育厅自然科学重点科研基金(12ZA132)和四川省高校科研创新团队建设计划基金(12TD008)

O482.5

A

1001-8395(2017)04-0503-08

10.3969/j.issn.1001-8395.2017.04.013

*通信作者简介： 吴绍全(1963—)，男，教授，主要从事介观物理的研究，E-mail：2963434972@qq.com