基于列车运行最小能耗的优化控制研究
2017-09-15杨永清
马 婧, 杨永清
(西南交通大学,四川成都 610031)
基于列车运行最小能耗的优化控制研究
马 婧, 杨永清
(西南交通大学,四川成都 610031)
文章通过对列车运行过程的分析,利用再生制动能,以能耗最小为目标,从而建立优化控制模型。利用等时间步长Δt简化模型算法,并通过遗传算法寻求全局最优解,并利用MATLAB编程计算以验证模型的有效性,得出列车运行工况与其能耗的关系,从而达到优化控制列车运行的目的。最后求得节能运行的速度曲线图,为今后类似的工程或实际列车运行控制提供节能方案。
列车优化运行控制; 节能; 再生制动能; 遗传算法
轨道交通系统的能耗是指列车牵引、通风空调、电梯、照明、给排水、弱电等设备的能耗。根据统计数据,列车牵引能耗占轨道交通系统总能耗40 %以上。在低碳环保、节能减排日益受到关注的形势下,针对减少列车牵引能耗的列车运行优化控制近年来成为轨道交通领域的重要研究方向[1]。
列车在站间运行时会根据线路条件、自身列车特性、前方线路状况计算出一个限制速度,列车运行过程中不允许超过此限制速度,限制速度会周期性更新。在限制速度的约束下列车通常包含牵引、巡航、惰行和制动四种运行工况。如果车站间距离较短,列车一般采用“牵引-惰行-制动”的策略运行。如果站间距离较长,列车通常会采用牵引到接近限制速度后,交替使用惰行、巡航、牵引三种工况,直至接近下一车站采用制动进站停车。因此寻求列车运行中的能耗最小模式成为了重中之重。
1 研究背景
1.1 动力学模型
列车在运行过程中,实际受力状态非常复杂,采用单质点模型是一种常见的简化方法。单质点模型将列车视为单质点,列车运动符合牛顿运动学定律。其受力可分为四类:重力G在轨道垂直方向上的分力与受到轨道的托力抵消,列车牵引力F,列车制动力B和列车运行总阻力W(图1)。列车牵引力F是由动力传动装置产生的,与列车运行方向相同,驱动列车运行并可由司机根据需要调节的外力。列车总阻力是指列车与外界相互作用引起与列车运行方向相反,一般是阻碍列车运行的、不能被司机控制的外力。按其形成原因可分为基本阻力和附加阻力。列车的基本阻力是列车在空旷地段沿平、直轨道运行时所受到的阻力。该阻力是由于机械摩擦,空气摩擦等因素作用而产生的固有阻力。列车由于在附加条件下(通过坡道、曲线、隧道)运行所增加的阻力叫做附加阻力。附加阻力主要考虑坡道附加阻力和曲线附加阻力。制动力B是由制动装置引起的、与列车运行方向相反的、司机可根据需要控制其大小的外力[2]。
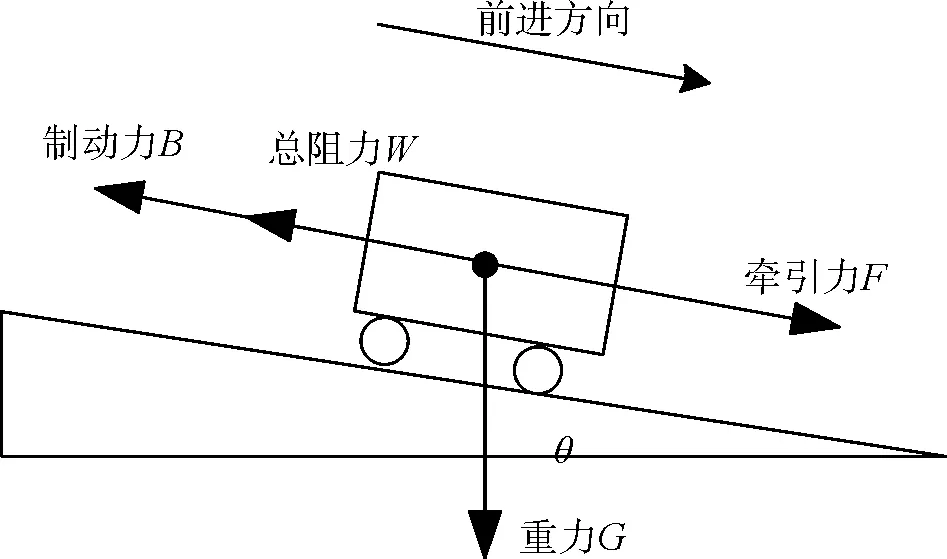
图1 单质点列车受力分析示意
1.2 运行时间与运行能耗的关系
当列车在站间运行时,存在着多条速度距离曲线供选择,不同速度距离曲线对应不同的站间运行时间和不同的能耗。一般认为,列车站间运行时间和能耗存在近似图2中的反比关系。注意增加相同的运行时间不一定会减少等量的能耗。列车站间运行时间与能耗变化的趋势影响能耗的减少。

图2 站间运行时间与能耗关系
2 列车运行研究初步分析
2.1 问题的提出
设想共计100列列车以间隔H={h1,…,h99}从A1站出发,追踪运行,依次经过A2,A3,……到达A14站,中间在各个车站停站最少为Dmins,最多为Dmaxs。间隔H各分量的变化范围是Hmin~Hmaxs。建立优化模型并寻找使所有列车运行总能耗最低的间隔H。要求第一列列车发车时间和最后一列列车的发车时间之间间隔为T0=63 900 s,且从A1站到A14站的总运行时间不变,均为2 086 s(包括停站时间)。假设所有列车处于同一供电区段,跟踪列车(后车)速度不能超过限制速度Vlimit,且满足条件高峰时间(早高峰7 200~12 600 s,晚高峰43 200~50 400 s)发车间隔不大于2.5 min且不小于2 min,其余时间发车间隔不小于5 min,每日240列。
2.2 模型的假设及初步分析
列车的牵引和制动力是列车优化控制的输入变量,列车的位移和速度是列车的状态变量,列车运动满足动力学方程,状态约束是线路限速和区间时间,优化目标为能量消耗最小。在确保安全运行、满足线路限速约束、机车性能约束和运行时间约束的条件下,充分利用线路坡道,以能量消耗最小为控制目标,得到列车最优化控制策略[3],建立单列车优化控制模型。因此对于列车的优化模型,现有假设如下:列车的牵引和制动力是连续的,可以为包络线下任意点力的值;列车的制动特性可以满足列车在线路任意位置安全减速;将列车视为一个质点,即单质点列车模式,以列车中部作为计算位置;在单列车优化控制模型中,假设时间步长Δt内加速度不变。
当列车处于牵引阶段,在城市轨道交通列车的牵引过程开始时,首先经过1 s左右的起动时间,将牵引力增至最大(即加速度增至最大)。在速度上升至一定程度后,逐渐减小牵引力,使速度曲线较为平滑地逐渐接近巡航速度,从而进入惰行过程。一般而言,加速过程可分为起动阶段、迅速加速阶段、缓慢加速阶段三个阶段。
为使运行最节能,此阶段列车以最大牵引力为限进行牵引,列车所受合力如式(1)所示:
(1)
式中:C1为第1种工况(牵引阶段)列车所受合力(kN);F为当前列车实际最大牵引力(kN);W为列车运行总阻力(kN)。
而当列车处于巡航阶段时,其运行工况是牵引与惰行交替进行的,如果有长大的下坡道,可能出现制动工况与惰行工况交替的情况,由于波动较小,近似列车为匀速运行,故此阶段列车所受合力C2=0。
当列车处于惰行阶段时,在满足站间运行时分的前提下,列车进站时适当增加惰行运行,以降低制动前的列车运行速度将有利于列车牵引能耗的降低。在惰行阶段,机车既无牵引力也无制动力,列车依靠惯性前进,由于只有运行阻力作用,因此,列车运行能耗最小。此阶段列车所受合力如式(2)所示:
(2)
式中:C3为第3种工况(惰行阶段)列车所受合力(kN);W为列车运行总阻力(kN)。
最后当列车处于制动阶段时,在列车的正常运行中,当列车的运行速度即将超过限速或需进站停车时,将对列车施加制动力,以降低其运行速度。在计算列车制动过程时通常只考虑列车沿轨道的前进方向(纵向)上所受作用力,主要包括基本运行阻力、制动力以及线路产生的附加阻力[4]。
为使列车运行最节能,此阶段列车以最大制动力为限进行制动,列车所受合力如式(3)所示:
(3)
式中:C4为第4种工况(制动阶段)列车所受合力(kN);W为列车运行总阻力(kN);B为实际制动力最大值(kN)。
将列车运行区间利用时间步长Δt等步长划分为j个子区间(j→∞),根据牵引计算的递推公式(1),可得出列车在第i工况第j步长所受合力Cij(v,s)函数如式(4)所示:
(4)
式中:S(tj)为第j步列车走行距离(m);S(tj+1)为第j+1步列车走行距离(m);Δt为时间步长(ms);v(tj)为第j步速度(m/s);v(tj+1)为第j+1步速度(m/s)。
(5)
式中:Cij为第i种列车运行工况下第j步长的列车合力(N);S(tj)为第j步列车走行距离(m);S(tj+1)为第j+1步列车走行距离(m);v(tj)为第j步速度(m/s);v(tj+1)为第j+1步速度(m/s);M为列车质量(kg)。
因此当列车在不同运行工况下,若不考虑附加阻力的影响,其所受合力C与列车当前速度v的关系图可如图3所示。
2.3 列车的再生制动能利用分析
建立以能耗最小为目标的列车运行优化控制模型的前提就是熟悉列车运行过程和再生制动能的利用,在此基础上认清列车运行节能策略的实质。
城市轨道交通运行具有不同于传统铁路列车运行的特点,决定了再生制动能的利用潜力远远大于铁路,再生制动能的利用率受列车的发车频率影响较大。由于城市轨道交通线路的相邻车站间距较短,列车正常运行中需要频繁制动,故而在再生制动过程中所产生的总能量是非常可观的,甚至超出地铁机车牵引消耗的总电能的30 %。故目前城市轨道交通普遍采用再生制动[5]。
再生制动能的利用是一个复杂的过程,其中包含电能转化为动能、动能转化为电能、电能传输中的损耗等阶段。反馈的制动电能一部分会馈送到直流牵引网并被该供电区段上的其他机车吸收。一般认为,当某辆列车制动的同时,有其他机车正处于加速阶段时,制动电能的利用效率较高。因此,可通过合理确定列车开行方案中的相邻列车追踪间隔以及停站时分,达到最大化线路运行过程中列车制动时段与加速时段的重合部分,提高制动再生电能的利用率。
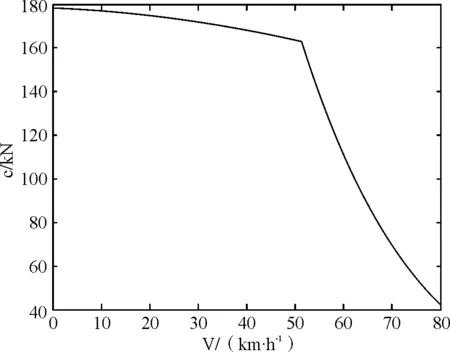
(a) 牵引阶段i=1
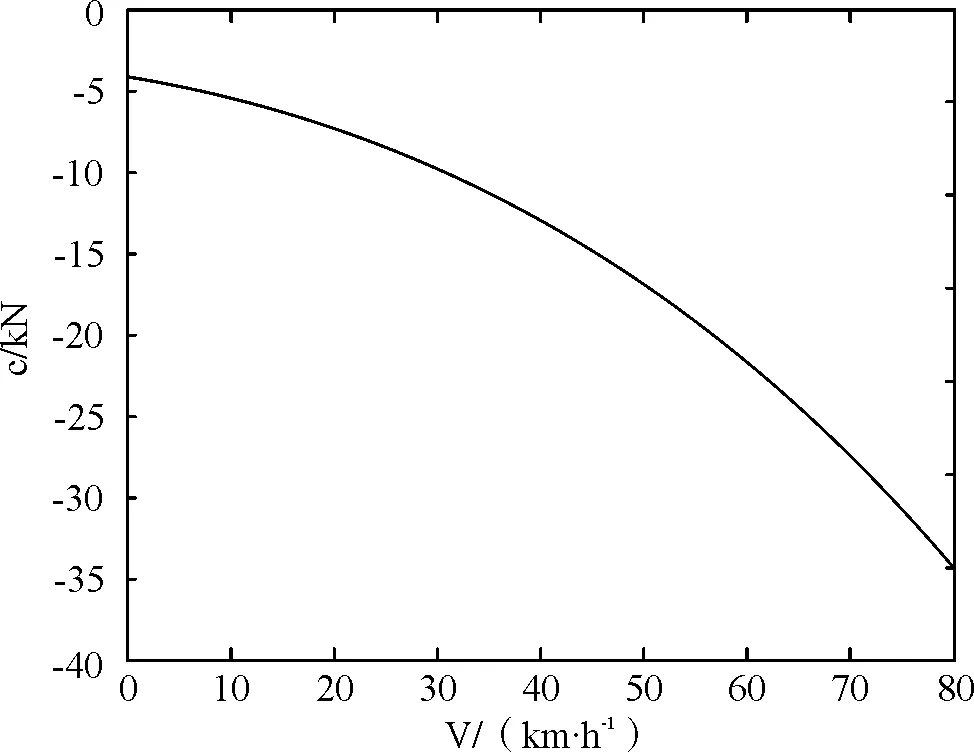
(b) 惰行阶段i=3
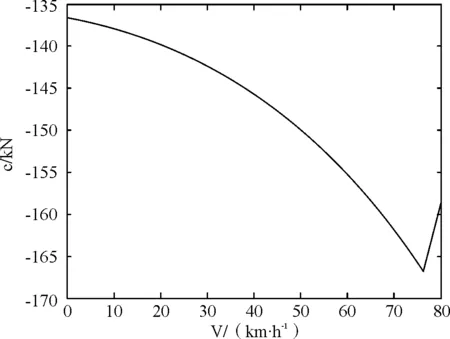
(c) 制动阶段i=4图3 列车不同运行工况下合力C-v图注:由于巡航阶段列车所受合力为0,故无巡航阶段。
因此再生制动能利用模型如图4所示,列车i+1在制动时会产生能量Ereg,如果相邻列车i处于加速状态,其可以利用Ereg,从而减少从变电站获得的能量,达到节能的目的。如果列车i+1制动时,其所处供电区段内没有其他列车加速,其产生的再生能量除用于本列车空调、照明等设备外,通常被吸收电阻转化为热能消耗掉。
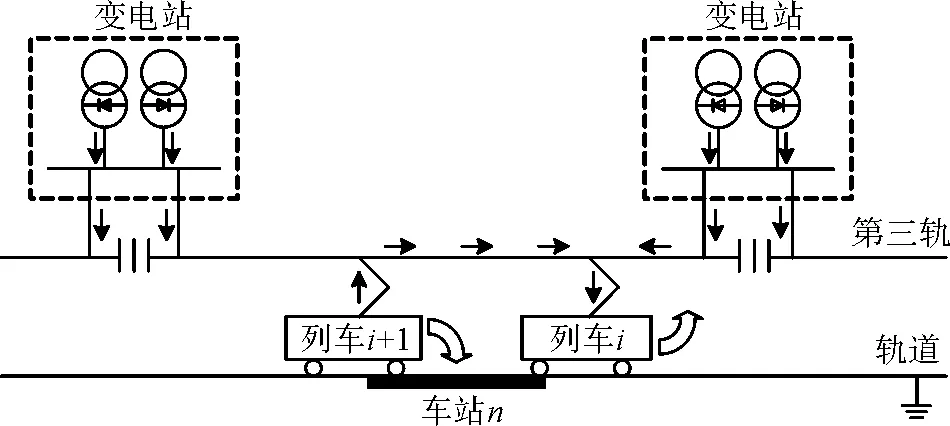
图4 再生能量利用示意
3 列车模型建立与求解
通过对列车建立非线性目标模型,利用遗传算法对模型进行求解。经研究表明,当加速阶段以最大牵引力加速,中间阶段采用匀速运行和尽可能惰行;进站阶段以最大值动力制动,即列车在区段内的运行工况从牵引—惰行—制动时为最优。如果区间运行时间比较富裕,速度越低,列车能耗越小[6]。
节能运行控制的目标就是寻找一系列列车运行方式的转换点,将列车运行的各个区间联系起来,同时满足正点的要求。以节能优化目标的列车运行控制模型如式(6)。
(6)

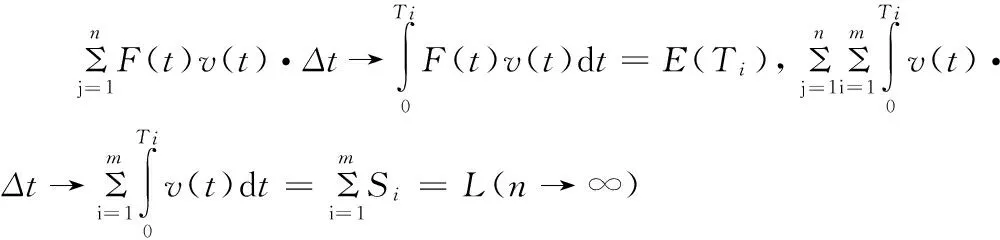
按照最节能的列车运行工况运行,假定列车从A6站出发到A7站,以最大牵引力启动加速,计算发现其不会超过限速点,计算发现当列车速度达到55 km/h时,列车当前位置与A6站的距离L6b=132.5 m>L6B,故列车从A6站到A7站运行过程中,不会受限速点影响其牵引阶段。
因此,为简化计算,可将A6到A7视为一个区段,在该区段的列车工况i=1,2,3(即式(6)中m=3),其顺序如下:
(2)惰行阶段直至达到安全制动点,确保列车安全制动进站停车;
(3)制动阶段以最大制动力制动减速进站停车,使得最终速度v(T)=0。
故A6站到A7站距离中L67=1 354 m,牵引阶段列车行驶路程为S1,惰行阶段列车行驶路程为S2,制动阶段列车行驶路程为S3,即L67=S1+S2+S3=1 354 km。
根据式(6),采用遗传算法,通过MATLAB编程求解得到列车从A6出发到达A7的最节能运行速度距离曲线(V-S)如图5所示。
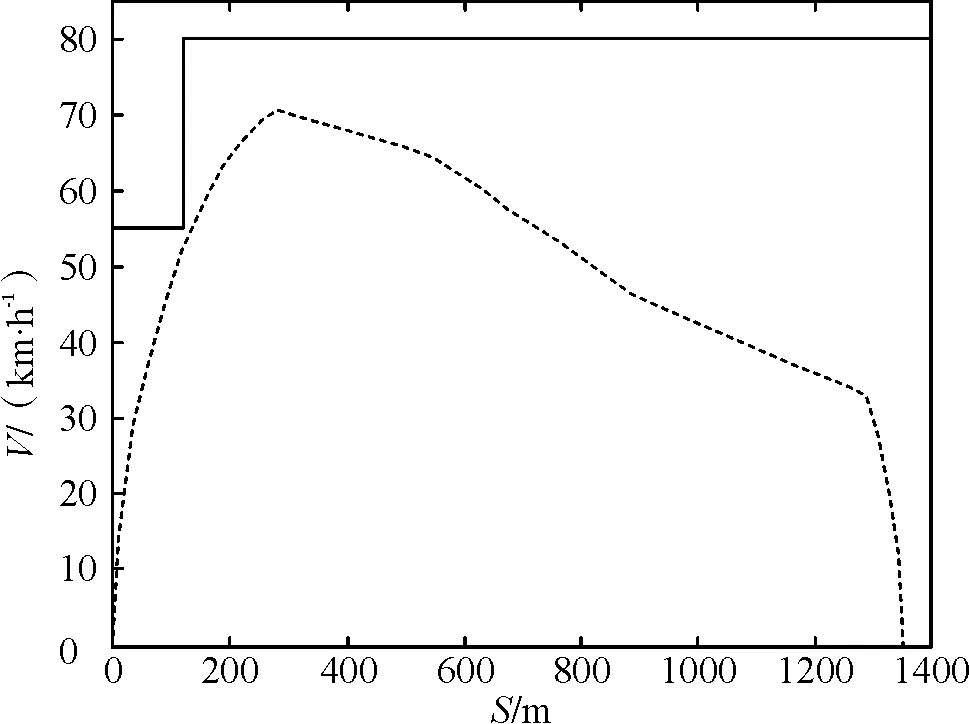
图5 列车从A6出发到达A7的最节能运行速度距离曲线(V-S)
列车总运行时间在各区段的分配需要增加时间约束[5]如图6所示。
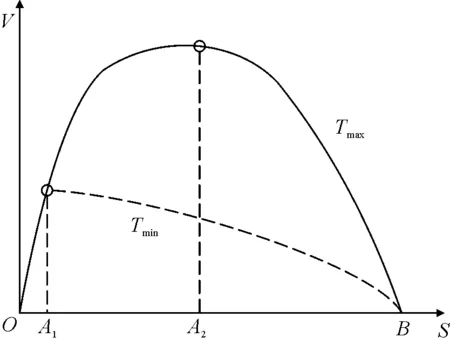
图6 列车运行V-S图
当列车牵引加速到速度最大(即到达A1点)后采用惰行工况最终到终点B停车(即A1-B段),列车总运行时间为最小值Tmin;当列车牵引加速到速度最大(即到达A2点)后采用最大制动力制动到终点B停车(即A2-B段),列车总运行时间为最大值Tmax。故增加的时间约束为Tmin≤T≤Tmax。
根据模型式(6)作出改进优化模型式(7)。
(7)

为简化计算,由式(7)可知列车在A7站停站时间45 s,对模型最优解并无直接影响,对最终的最节能运行速度距离曲线(V-S图)也无影响,故不作考虑。
本题求解可简化为,将A6站到A7站划分为A6站到A7站、A7站到A8站两个区段,每个区段的列车运行工况均相同,且列车运行工况i=1,2,3(即式(6)中m=3),其顺序如下[7]:
(1)两区段的牵引阶段均以最大牵引力加速至接近该区段的限制速度v7=80 km/h、v8=80 km/h;
(2)两区段的惰行阶段均惰行行驶到达安全制动点制动,确保列车安全制动进站停车;
(3)两区段的制动阶段均以最大制动力制动减速进站停车,使得列车到达A7站和A8站的最终速度均为v(T)=0。
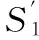
根据式(7),采用遗传算法,通过MATLAB编程求解得到列车从A6出发到达A8的最节能运行速度距离曲线(V-S)如图7所示。
图7 列车从A6出发到达A8的最节能运行速度距离曲线(V-S)
4 结论
(1)通过建立列车的数学模型,并以列车运行过程中最小能耗为目标,通过调整列车运行的工况转换点及列车运行策略,实现再生制动能的利用,降低全线列车总能耗[8]。
(2)通过详细分析列车运行中的牵引、惰行、制动过程,明确了增加相邻列车牵引阶段和再生制动阶段的重叠时间是提髙线路再生制动能利用率的有效途径。
(3)引入遗传算法,由于遗传算法理论上具有全局优化性能、通用性强、不需要函数的导数且适用于并行处理的随机化搜索算法。这种算法具有严密的理论依据,而不是单纯凭借经验,理论上可以在一定时间内找到最优解或近似最优解,因此其对列车的牵引控制进行了优化,达到了兼顾时间和节能的效果,计算结果表明在保证节能的同时能减少列车的运行时间。
[1] 朱金陵,李会超,王青元,等.列车节能控制的优化分析[J].中国铁道科学,2008,29(2):104-107.
[2] TB/T 1407-1998 列车牵引计算规程[S].
[3] 刘宝林. 地铁列车能耗分析[J]. 电力机车与城轨车辆, 2007,30(4):65-68.
[4] 石红国, 彭其渊, 郭寒英. 城市轨道交通牵引计算模型[J]. 交通运输工程学报, 2005, 5(4):20- 26.
[5] Su S, Tang T, Li X, et al. Optimization of multitrain operations in a subway system[J]. Intelligent Transportation Systems, IEEE Transactions on, 2014, 15(2): 673-684.
[6] 冯佳. 考虑节能目标的城市轨道交通列车运行行为优化研究[D]. 北京:北京交通大学,2014.
[7] 唐海川,王青元,冯晓云.地铁列车追踪运行的节能控制与分析[J].铁道学报,2015(1):37-43.
[8] 丁勇,毛保华,刘海东,等.列车节能运行模拟系统的研究[J].北方交通大学学报,2004(2):76-81.
国家自然科学基金《超强高韧性树脂钢丝网混凝土及在预应力板梁板加固设计研究》(编号:51508474)
马婧(1994~),女,硕士研究生,研究方向为既有桥梁结构损伤识别与健全性评估理论;杨永清(1965~),男,教授,研究方向为既有桥梁结构损伤识别与健全性评估理论。
U260.15+3
A
[定稿日期]2017-03-10
