PFC中应力测量圆半径浅析

2017-09-15章春炜路军富钟英哲

四川建筑 2017年4期

关键词：岩爆阻尼半径

章春炜，路军富，钟英哲

(成都理工大学, 四川成都 610059)

PFC中应力测量圆半径浅析

章春炜，路军富，钟英哲

(成都理工大学, 四川成都 610059)

在PFC软件中，可用应力测量圆来提取模型中的应力值，但是不同半径的应力测量圆所提取的应力则不同。文章通过数值模拟与实际计算的方法相结合，研究不同半径的应力测量圆所提取的应力值与实际应力值的拟合程度。研究结果表明：在颗粒半径最大为30 mm、最小半径为5 mm情况下，半径为0.3 m的应力测量圆所提取的应力值与实际应力值拟合度最高。

PFC；应力测量圆；半径；模型；应力

随着颗粒离散元方法应用越来越广泛，PFC作为一种典型的离散元软件，在岩石类材料基本特性、颗粒物质动力响应等问题中具有较多的应用。朱焕春[1]结合阐述了PFC应用现状，并结合工程实例说明PFC可以针对性的解决一些岩土体问题。周国庆[2]运用PFC 2D研究颗粒流程序中的阻尼参数的适用性，得出了在PFC 2D中局部阻尼和黏性阻尼的定义及适用范围。吴顺川[3]通过对比分析室内卸载岩爆试验与数值模拟研究，得出PGC 3D数值模拟可以部分代替室内试验。王延可[4]得出用PFC 数值模拟试验研究岩爆特性的效果非常好。国内学者对用PFC的实际应用得出了较多的研究成果，但是对于PFC软件内置功能的研究较少。

本文通过数值模拟方法建立砂卵石地层模型，并在重力作用下达到平衡，研究不同半径应力测量圆所提取的应力与实际计算应力的拟合程度，得出下最合适的应力测量圆的半径。

1 应力测量圆理论

应力是一个连续的量，因此不存在于每个粒子上，因为介质是离散的。在离散点的PFC 2D模型中，接触力和粒子位移都能被计算。这些矢量在研究微观行为时十分有用，但不能直接转移到一个连续模型。因此从微观模型到连续模型需要通过公式转化，转化公式如：

(1)

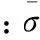
由公式(1)可知，平均应力主要与测量圆的体积有关，而测量圆大小则与所取半径有关，所以确定所需应力测量圆的半径是重要的一步。通过不同应力测量圆的半径所取得的应力与计算所得应力相比较，最终确定所需应力测量圆的半径。

2 应力测量圆半径确定

用半径为0.2 m、0.3 m、0.4 m、0.5 m的应力圆获取中密天然含水率状态下PFC 2D离散元模型自重应力平衡后的应力值，该模型宽50 m，高45 m，土颗粒密度ρ=2.0 g/cm3，颗粒半径最小为5 mm，最大颗粒半径为30 mm。

由于该离散元模型中，没有构造应力，只有自重应力。对于土体自重应力计算可通过公式：σ=γz=ρgz得出，并将计算得出模型每一层的自重应力与每一层应力测量圆测得的自重应力进行比较，所得对比曲线如图1所示。

分析图1可得，在半径R=0.2 m时应力测量圆所得自重应力曲线波动较大，并且最大值远远高于计算值。因此在

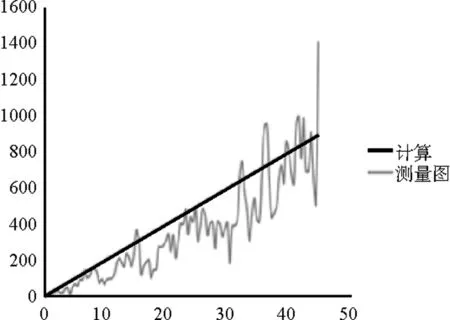
(a) R=0.2 m

(b) R=0.3 m

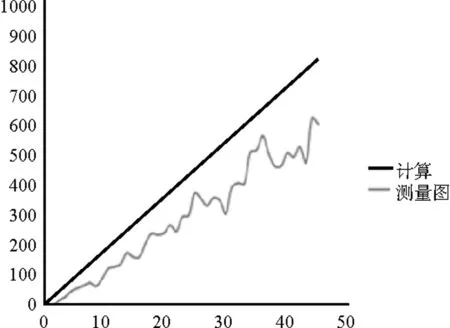
(d) R=0.5 m图2 计算自重应力与测量圆自重应力对比

该颗粒级配下，用半径为0.2 m的应力测量圆不能准确测得颗粒之间的应力，可以直接排除。对于应力测量圆半径为0.3 m、0.4 m、0.5 m时，其自重应力曲线图波动都比较小。对比应力测量圆半径为0.3 m、0.4 m时，应力测量圆半径为0.5 m时所测得的自重应力曲线与计算所得自重应力曲线拟合度较差。为了更好地确定各半径应力测量圆所得自重应力曲线与其对应的计算所得自重应力曲线的拟合程度，计算了各半径应力测量圆所得的自重应力曲线与目标直线的拟合度，拟合度取值见表1。