基于培养建模能力的力学竞赛资源库建设

徐 粲， 胡一知， 邓 玮， 李 飞， 王勇洁， 巫绪涛

(合肥工业大学宣城校区建筑工程系，安徽宣城 242000)

基于培养建模能力的力学竞赛资源库建设

徐 粲， 胡一知， 邓 玮， 李 飞， 王勇洁， 巫绪涛

(合肥工业大学宣城校区建筑工程系，安徽宣城 242000)

力学建模是联结力学与工程应用最为重要的纽带，也是力学应用通向工程技术进步的一座桥梁。文章结合高校学生学习经验，进行力学竞赛资源库建设。文中分别从知识点阐释方式、知识点拓展、对数学能力的强化三方面概括阐述了资源库由浅入深、循序渐进，通过提炼问题共性，由普遍至特殊拓展问题，解决问题的建立原则，以及资源库为培养学生建模能力所采取的方法。

力学竞赛； 材料力学； 资源库

多年来，随着各高校对力学的重视程度不断加深，力学教学取得了较丰富的成果。并且，伴随其应用的发展而不断充实，经过国家立项的面向21世纪系列课程改革，力学课程已经取得了一系列成果[1]。其中，力学竞赛培养了学生的科学精神、科学态度和科学方法，以及培养学生的意志品质、思维品质、实践能力和自学能力。在竞赛辅导的同时也丰富了教师的专业知识，更重要的是增强了教师自身的创新意识和创新实力，这将直接或间接地对创造型人才的培养产生积极的影响。但各高校对力学资源库的建设工作往往散见于有关力学和工程应用的文献、力学竞赛的辅导教材中，集中思路、强调过程的资源库尚不成熟。尤其是力学竞赛教学资源库的建设和应用还存在着很多问题，由于力学竞赛的知识广度和思维难度都远超本科阶段学习，其资源库的建设也涉及到方方面面的问题。

多媒体技术的飞速发展,给现代教育带来了生机与活力[2]。本文结合高校学生对材料力学[3]的学习经验，开展基于培养建模能力的力学竞赛资源库建设，以提高学生力学建模能力。

现分点阐述帮助培养学生力学建模能力而采用的具体方式。

1 基础知识阐释方式

本资源库对基础知识方面的阐述不同于常规课堂学习的方式。后者常从基本假定出发，一步步推导，得出结论，结合具体实例强化对知识的理解。而本资源库基于学习对象主要为完成《材料力学》学习的学生，在介绍典型例题思路的同时系统地归纳串联每个知识点，具体阐述各个知识点在例题中的应用方式。相比于常规学习中的建立模型推出结论，资源库着重培养的是利用结论解决实际问题的能力。例如，在对一部分悬臂、一部分支撑在已知曲率台座上梁的问题分析中，课件内由梁与台座贴合这一结论结合相应知识点，得出曲率与弯矩之间的关系式，从而完成对此类问题的分析与解答。

2 关键知识应用拓展

本资源库建设的目的为培养学生的力学建模能力，故其课件中除了对基础知识进行归纳总结外，还对多个知识点进行了更具深度和广度的拓展。思路分析过程循序渐进，由点至面，由基础问题中的小知识点为起点拓宽至多个重要知识点，逐步发现并解决更具难度和深度的问题，旨在帮助学生在面对工程问题时，能够“化繁为简”，从而建立一个合理的力学模型进行分析求解。以达到提高学生建模能力与力学素养的预期效果，下面举例阐述。

2.1 弯曲切应力问题分析

在基础知识部分中，我们已完成了矩形截面梁弯曲切应力的推导。可以发现，其中所运用的切应力互等定理可作为共性继续推广至对任意梁横截面弯曲切应力的推导中。

进而引入对于T型梁弯曲横截面的切应力分析，利用之前推导实腹构件横截面切应力的经验，同样将构件从纵截面处截开，但此时所截取的两个纵截面中， 1-1截面已不同于闭口构件中恒为水平面的纵截面(图1)，此时，1-1截面法线方向呈水平方向见图1，而矩形截面梁的纵截面法线方向衡垂直于水平方向。

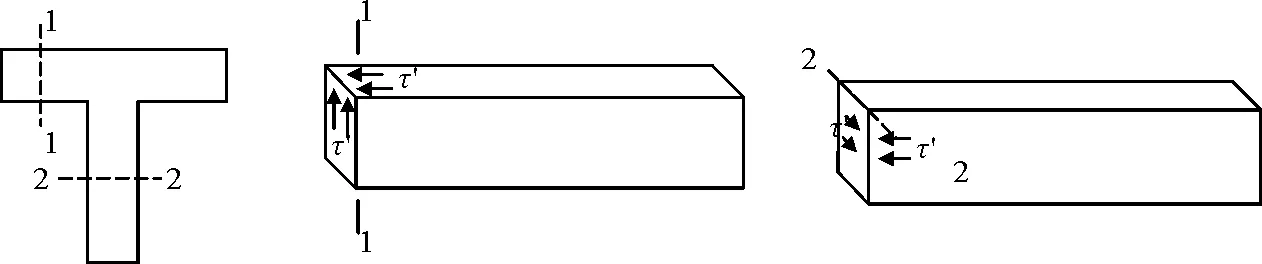
图1 T型梁弯曲切应力推导隔离体截取位置

然后用类似的分析方法，取隔离体见图1，利用切应力互等定理，沿轴向建立平衡方程，推导出开口薄壁横截面切应力公式。

再推广至任意横截面弯曲切应力推导。例如，梁受均布轴向荷载时的弯曲切应力推导见图2。类似之前的推导，同样取一隔离体如图2、图3所示，由受力分析可知，基于切应力互等定理，但特殊在于此时正截面切应力中应再加上均布轴力的作用，然后建立轴向力的平衡方程求解，推导出此时正截面切应力的解析式。

图2 受均布轴向力作用梁

图3 隔离体

此例运用上例中切应力推导的方法，将问题拓宽，再结合此类问题的范式，推广至特殊情况，然后解决问题。

课件中大量运用此类方法，在加深问题难度的同时，基于难度的逐步提升，对多种情况进行对比，提炼问题的共性，结合各实际问题的特性，建立相应力学模型进行分析，更有利于学生理解此类难度较大的问题。

2.2 对称与反对称问题分析

首先从内力图及变形的对称与反对称情况开始引入，当两端简支梁受两个对称集中力作用时(图4)，弯矩图呈对称

形式，而剪力图呈反对称形式(图5)。

图4 简支梁受两个对称集中力作用

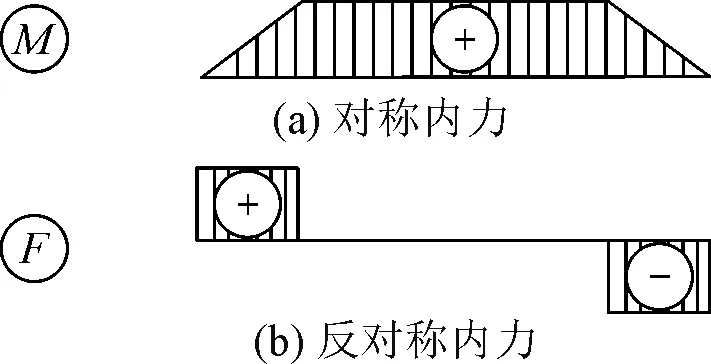
图5 对称反对称内力

之后，结合能量法判断截面所应存在的内力，引出对称与反对称超静定结构的辨别。对称性与反对称性同时存在时(图6)。

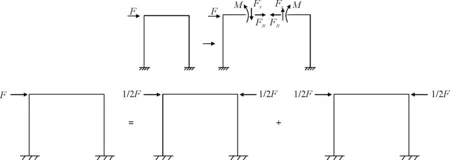
图6 对称反对称问题

方法1：将此结构分解为对称受力与反对称受力的叠加见图6，将原结构进行求解需建立一个三元一次方程组简化为对一个二元一次方程组和一个一元一次方程的求解，简化运算。

方法2：利用结构对称而荷载不对称，直接将结构从对称处截开，得截面处呈正对称分布的轴力和弯矩，以及呈反对称分布的剪力。然后在运用力法求解时，基于此时单位力在两侧结构的对称与反对称性，简化计算见图6。

本例中，课件在完成对内力图求解后，并未结束于此，而是基于此特殊内力图中弯矩图的对称和剪力图的反对称进行了更深一步的讨论，引出结构及内力具有对称性或反对称性时的求解方法。比如在薄壁圆环径向受力的问题中，取1/4隔离体作分析求解。

课件中，运用此类方法在传统课堂学习的基础上，简化各类题型的求解方法，降低解题思维的复杂程度，丰富学生的力学知识的同时，培养了学生对实际工程的处理能力。

2.3 不同材料组合梁的横截面应力分布问题分析

首先结合组合梁与单一材料梁的共性，从“平面假定”的概念出发，推出“截面应变连续”的几何关系。然后由“单向胡克定律”：

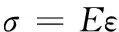
利用这一本构关系，得到截面上各点处的应力分布状态，应力沿截面高度不连续见图7。由静力等效原理，通过改变截面尺寸将不同材料的组合梁换为同种材料的T型梁见图7。

图7 组合梁问题

指出两者在纯弯曲状态下轴力为零的共性。结合《材料力学》中，对纯弯曲梁中性轴位置的推导过程和方法，以此来确定此T型梁中性轴的位置。最后，由截面外力矩与截面应力合力矩平衡的条件，得到组合截面梁横截面的应力大小。

本例中，课件将对梁横截面应力求解拓展至对不同材料组合梁的横截面应力求解，通过从基础出发，加深难度，然后结合问题的共性和特性，进行分析求解。

整个资源库的建设都类似以上三点情况，整体的建设内容循序渐进、深入浅出，首先归纳知识点找出问题的共性，而后加深难度至具特性的问题，由普遍至特殊，拓宽知识广度。这既帮助学生梳理课堂知识，又为教师上课提供了便利。同时，让学生在课堂上就能学会举一反三。

3 力学问题数学分析

部分力学问题的难点，不在于力学知识，而在于数学计算。故在资源库的建设中，课件在基础知识的归纳和拓展部分，还植入数学知识。在一些特定问题上，通过对数学知识的运用，建立了相应力学问题具力学性质的数学解析式。从 数学上对力学问题进行分析，突出对学生数学能力的培养，也加强了学生的综合建模能力：

3.1 压杆稳定问题

在弯曲章节中，我们曾推导出挠曲线近似微分方程中挠度二阶导数与梁所受弯矩的关系：

EIy″=-M(x)

引入记号，

可得弯曲问题与稳定性问题所共同具有的挠曲线二阶微分方程：

y″+k2y=0

然后对y在求两次导，得两者共有的挠曲线四阶微分方程：

此时弯曲问题以及稳定性问题，都可结合相类似的位移边界条件和静力边界条件，完成对上述两个微分方程的求解。

而两个问题的不同之处在于，弯曲问题对挠曲线近似微分方程的求解中，目的为求解挠度y的具体表达式，而在稳定性求解中，目的在对方程通解系数进行求解得到压杆稳定的临界力。显然，无论是对弯曲问题的求解，还是对稳定性问题的分析，其中大量使用的数学技巧都在提高学生的数学素养，通过对比，加深学生对相应知识点的理解。

3.2 平面应力状态分析

对平面应力状态微元体受力分析，建立任意截面位置的应力状态矩阵表达式，从而可以实现应力的坐标变换，进行实际问题的分析。此处运用线性代数对力学问题进行分析，进而培养学生的数学能力。

以上两个问题的分析中，运用了常微分方程、矩阵变换等多种数学知识。数学技巧作为工科学生的一项必备素质，在力学建模中更是不可或缺。

课件中除了上述问题中所用到数学技能外，还在其他更多问题的具体分析中也用到了奇异积分、特殊函数等多项数学知识。在对力学问题求解中，通过对各类数学技能和数学知识的运用，提高了学生的数学水平，也增进了学生的力学建模能力。

4 结束语

力学建模作为连接理论与实践的桥梁，在人才培养中占着举足轻重的作用。本文通过介绍力学竞赛资源库的几项特点，简单阐述了力学竞赛资源库对学生力学建模能力培养和力学素质提高中所采取的方法。通过此次对资源库的建设，也提升了笔者的力学建模能力和力学素养。本文以培养具有良好力学建模能力的学生为目的所进行的资源库建设虽然考虑了部分实际情况，但由于资源库使用时间短暂，还有更多的问题需在将来的不断实践中加以更正。

(指导教师巫绪涛系合肥工业大学副教授)

[1] 范钦珊，李绯，倪如慧， 等. 工程力学课程教学资源库的建设[J]. 中国大学教育，2004(4)：21-22.

[2] 宋祥红.岩土工程网络教学资源库的开发[D]. 西安： 长安大学，2005.

[3] 杨伯源.材料力学[M].北京：机械工业出版社，2002.

徐粲(1996～)，男，本科在读，土木工程专业。

TU311.41

A

[定稿日期]2017-08-08