基于静态应变测量试验的混凝土环箍效应有限元分析

杨亦凡, 金耕涛, 周 强, 林杰铵, 张文学

(北京工业大学，北京100124)

基于静态应变测量试验的混凝土环箍效应有限元分析

杨亦凡, 金耕涛, 周 强, 林杰铵, 张文学

(北京工业大学，北京100124)

混凝土是一种重要的建筑材料，单轴抗压强度是其一项重要的力学指标，然而环箍效应的存在会影响抗压强度实测值。文章为了探究其作用范围和影响效果，先假设一个理想的受力模型，根据第二强度理论做出假定，即混凝土试件侧面同时受到压力和弯矩作用，达到最大拉应变时横向受拉破坏。通过静态应变仪测量应变的方法对试验假设进行验证，证明了环箍效应的存在和此前假定的试件表面微元体的受力形式。以此为基础，使用ABAQUS软件，去除多余约束，对受力模型施加试验机量程外的荷载，进一步从固体力学的角度对环箍效应进行有限元分析。

混凝土； 环箍效应； 应变； 试验； 强度理论； 有限元分析

1 研究背景

1.1 问题提出

混凝土是一种重要的建筑材料，单轴抗压强度是其一项重要的力学指标。然而在对混凝土的抗压强度进行测定时，施压装置与混凝土试件受力面之间的摩擦力会对试件产生约束，从而对抗压强度标准值的测定产生一定影响，即环箍效应。环箍效应的存在对于混凝土材料的力学性能测定带来一定干扰。环箍效应的存在对混凝土材料力学性能的影响研究是一个值得探讨的问题。

1.2 研究现状和研究目的

按照我国现行规范，混凝土材料在进行单轴受压强度测定时忽略环箍效应对测定结果的影响，即不在混凝土试件与施压装置之间采取措施以减小摩擦或在实际强度测定时增加偏保守的换算系数，而是在混凝土构件和结构设计时在混凝土抗压设计值中留有安全余量。

对于混凝土环箍效应的分析，在理论计算的基础上，可以采用静态应变测量试验与有限元分析两种方法。对此，我们可以先假设一个环箍效应影响的混凝土试件的受力模型，再利用试验测定受压试块侧壁应变的方法，对假设中的模型进行验证，从不同角度验证研究环箍效应所造成的影响大小及其作用特征。

2 静态应变测量试验

2.1 基本思路

试验采用100 mm×100 mm×100 mm的正方体标准混凝土试块(混凝土强度等级C30)，利用分级加载的方式对试块进行加载，采用静态应变仪记录试块在不同方位的应变。理想状态的各向同性的均匀试块为单向压缩状态，则其表面的微元体应力状态和莫尔圆如图1所示，即45°方位上的线应变应满足广义胡克定律：

(1)

对于同一试块而言，υ应该是常数。但由于混凝土属于脆性材料，试块发生破坏时，断口的方位也应是45°方向断口贯穿。单向受力时，应力圆如图1所示。

图1 单向压力状态的莫尔圆

然而混凝土试件的情况较为复杂，根据格里菲斯(Griffith A.)的脆性断裂公式：

(2)

固体材料抵抗外加负荷的能力受限于其抗拉强度，理论抗拉强度σm与弹性模量E，单位面积的表面能γ和原子间的平均距离a0相关。然而，混凝土是一种复合材料，力学性能并非完全各向同性，且由于粗骨料与砂浆之间过渡区的存在，材料实际断裂拉应力与材料裂缝临界宽度的一半C有关，表达式为：

(3)

由式(2)、式(3)可见，混凝土材料自身微小缺陷带来的裂缝两段会形成应力集中，将外力放大了(C/a0)1/2倍，材料局部区域达到抗拉理论强度导致断裂，进而造成材料破坏。由马略特(Mariotte E.)的第二强度理论，混凝土由于最大拉应变受拉破坏，取试件侧面(非直接施加荷载面)几何中心处一个微元体，微元体同时受压、弯(剪)，试件受力示意如图2所示。

图2 试件受力示意

放样的微元体位于试件边缘(外侧)几何中心处，无横向正应力。平面应变物理方程为：

(4)

由于微元体σx=0，σy<0，则有：

(5)

由上式可推得：

(6)

且混凝土泊松比μ约为0.2，在弹性范围内，微元体εx:εy的绝对值大于混凝土的泊松比μ，同时由于混凝土抗拉强度远远低于抗压强度，横向拉应变应是混凝土试件破坏的决定因素。

2.2 试验方案

在实际情况下，如果材料受到环箍效应影响，则可以认为，位于试块表面距离几何对称轴相等的微元体在受压同时受到弯矩以及与压力垂直的拉力。由于施压设备整体刚度较大，难以直接测出弯矩，静态应变测量试验可以重点测量试件表面的线应变。静态应变测量试验采用如图3所示的贴片方案。

图3 贴应变片示意

2.3 试验概述

试验采用YL2118C静态应变仪。先进行预试验测定试块的材料弹性模量E。另选两块表面平整无裂纹的混凝土块，分别放在已贴好应变片的试块的上下。将三个试块一起放到压力机上进行加载。每级加载50 N，共加载4级。记下应变仪示数，绘制成线性图，根据其斜率计算材料弹性模量E。

开始正式试验后撤去靠下的试块，在靠上块和试验试块之间及试验试块下垫上铁板，然后对试验试件逐级加载。第一阶段从6 000 N开始加载，每级加载300 N，加载到9 700 N结束，记录每次加载的各应变片对应的应变仪示数，保持荷载。第二阶段每级加载变为1 000 N，加载到14 000 N止，其余步骤同上。第三阶段同上，只将每级加载变为10 000 N，记载到80 000 N为止，记录数据。

2.4 试验数据与分析

2.4.1 预试验

在预试验中测得的原始数据如表1所示，统计如图4所示。

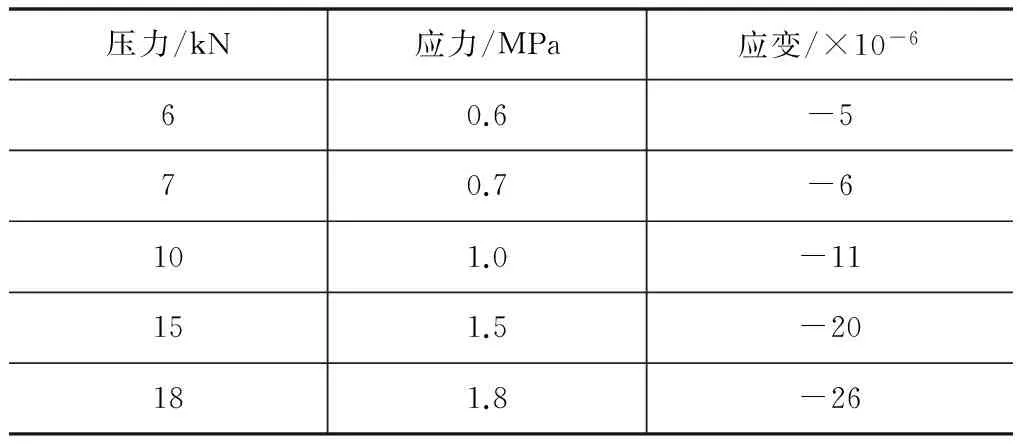
表1 预试验原始数据

图4 预试验应力应变关系

通过计算机拟合函数可以得到应力应变之间存在有如下函数关系：

y= -14.921x+2.5931

其中斜率的绝对值可以认为是实测试验试件的弹性模量E。通过该函数表达式即可推算出试块在其他压力值作用下的应变，作为从预试验中推算出的理论值和正式试验中的实测值进行比对。

2.4.2 正式试验

正式试验中的实测数据及经预试验推算的理论值如表2所示。

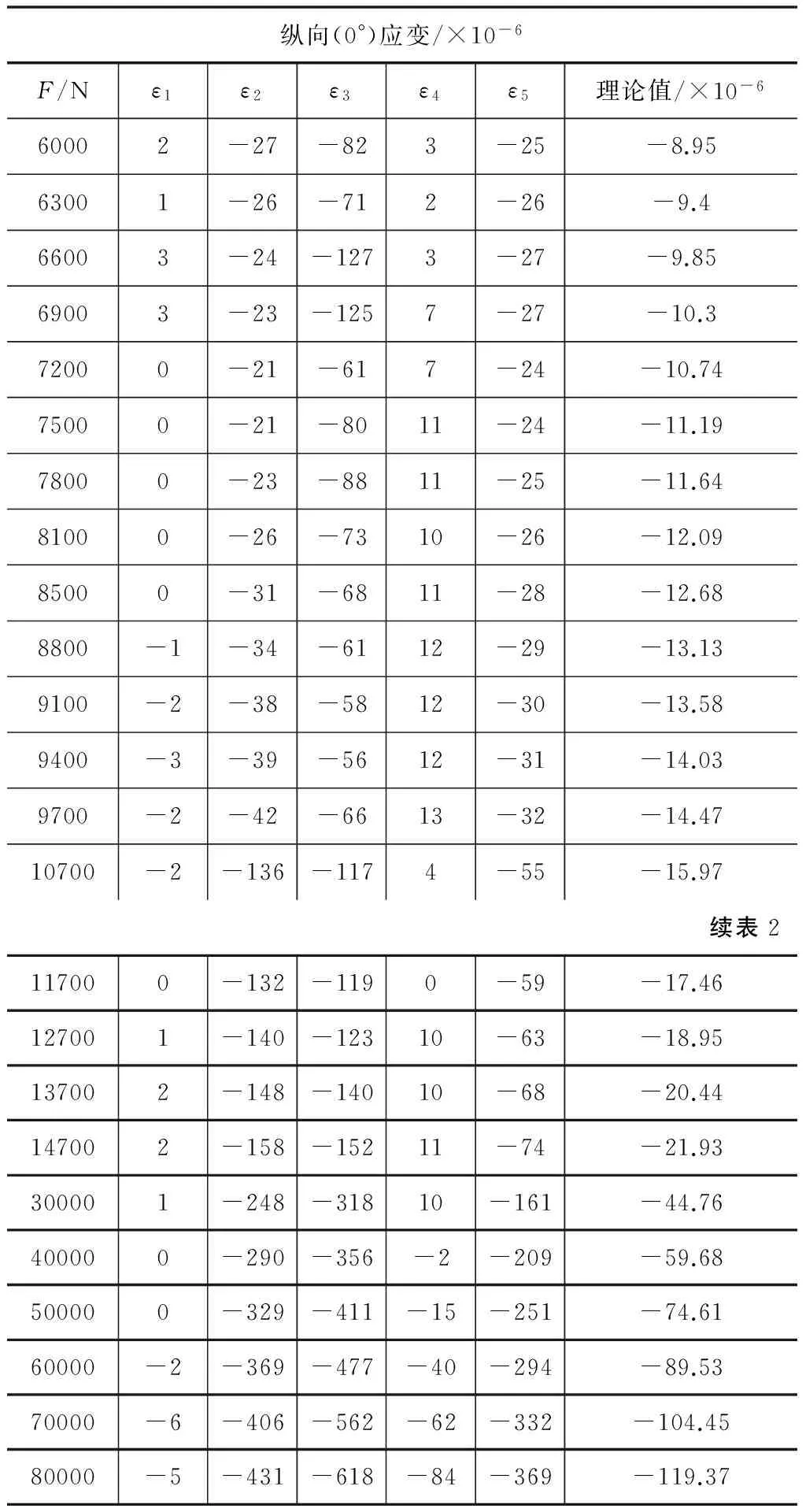
表2 正式试验原始数据

将原始数据表格分成三个区域进行制图，统计图如图5～图7所示。

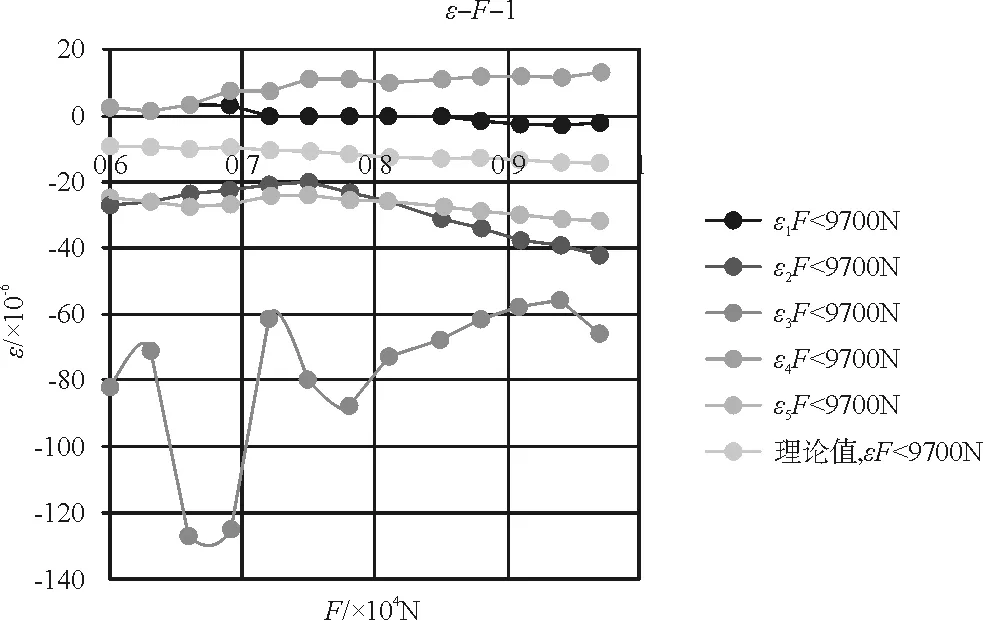
图5 6～9.7 kN应力应变

图6 9.7～14.7 kN应力应变

图7 F>30kN应力应变

从图5中可以看出，实测应变与应力的关系并不稳定，也未呈现很强的线性关系，所以暂不计入此阶段的应力应变关系。

从图6中可以看出，随着应力的增大，应变逐渐趋向于线性变化。但应力应变尚未表现出很强的线性规律，即大体呈现线性关系，但仍有所波动。此阶段可以作为一个过渡区域。

通过比较图5～图7可以看出，在压力大于30 kN时，应力应变关系的线性相关性比小于14.7 kN时的要强很多，大多数点都落在拟合直线上。

对比预试验中的数据可以发现，在预试验中，压力值虽然在6～18 kN之内，但已经表现出很好的线性关系。但在正式试验中，可以看到各应变片的线性关系都不好，尤其以应变3最为典型。但到了压力值较大时(F>30 kN)，所有应变片均发现具有良好的线性应力应变关系，应变3更是如此。

于是可以得出结论：环箍效应在压力值较小对应力应变的线性干扰较大，在压力值较大时则对其线性关系干扰较小。

其次，对比图5～图7，应变4都以不同程度出现了正应变，虽然其实测值并不总是正值，但根据表2中的数据显示，其出现正应变次数较多。与此同时，和应变4位于同一平面的应变1也有不同程度的正应变。这就说明应变4出现正应变并非全部都是试验误差所导致，而是正应变真实存在。这一点就证实了假设中所谈及的“由于环箍作用，压力作用下本应是负应变的地方可能转化成正应变”的说法，从而再次证实了环箍效应真实存在。

根据试验原理中所提到的对称性，真正试验中由于尺寸所限，并未完全按照贴片方案所示进行贴片，而是将应变片1、4贴于同一表面，应变片2、5贴于同一表面，应变片3贴于单独一面，其高度位置按原理图不变。其中各个应变片实测应变均与理论值有明显差异，且各个实测应变也均不相同，由此可说明试块在压力机压力作用下并不是单向受压状态，分析各实测应变与理论值直接的差值见图8。

图8 实测应变与理论值的差值

从图8中可以看到，贴于同一表面上的应变片差值走势基本一致。在同一表面内满足距离施压装置越远，差值绝对值越小(差值1>差值4、差值2>差值5)。由此可以认为，在同一表面上，环箍效应随距离压力板的距离越大则干扰效应越小。但由图线还可以看出，除应变片4外，其他实测应变均呈现绝对值增大趋势，这就说明随着力的增大，环箍效应对应力应变的线性关系干扰减小，对应变的干扰作用逐渐增大。

试验发现，理想情况下的四面对称并不存在。虽然在实际操作中，加载装置对称，加载力对称，试块几何尺寸(正方体)对称，但试验实测发现，该混凝土存在有不均匀膨胀现象，即各个面的膨胀程度不同(图5～图8)，这一点也在后来的有限元分析中得到印证。

3 有限元分析

3.1 有限元分析思路

静态应变测量试验验证了环箍效应的存在，并肯定了此前基于第二强度理论的推测：混凝土试件在受到有约束的轴向荷载时，垂直于施压方向的最大拉应变是造成试件破坏的主要原因。然而横向的拉应变测量受到混凝土较小的弹性模量等因素的限制，更宜使用有限元软件进行分析。

对于理论中存在的非线性分析，采用ABAQUS软件建立平面模型，与实际试验一致的边长100 mm的正方形来模拟混凝土试件的侧面。正方形上下两面同时作为受压面和受剪面，承受轴向均布荷载和方向由外向里水平剪力，其中受压面的几何中心处剪力为0。为了能更为直观地观察横向拉应变和微元体受弯(剪)，模拟受压面不加变形约束且不设置材料的抗拉强度，同时施加高于静态应变测量试验的荷载以及横向剪力。

3.2 有限元分析结果

当施加轴向压力1 500 kN、水平剪力50 kN时，可以得到一个较为夸张的应力云图(图9)，试件各部位应力均超过1 000 MPa，且试件竖向出现明显的应力差，造成横向拉应变。同时，试件受弯较为明显，进一步验证了实际混凝土试件受压时外部微元体同时受压、弯(剪)的假设。

图9 压力1500kN剪力500kN应力云图

由于混凝土实际受压时静摩擦力并不恒定，所以有限元分析中可以改变压力与剪力的比值。增大压力至2 500 kN，剪力不变，应力云图如图10所示。由于压力-剪力比值减小，试件表面受弯程度降低，但应力差依然明显。同时，试件应力分布的不对称性逐渐显现，这也印证了应变试验中观察到的混凝土不均匀膨胀现象。

图10 压力2500kN剪力500kN应力云图

当压力达到7 500 kN且剪力仍保持在500 kN时，混凝土轴向压缩变形变得更加明显(图11)，此时由于剪力相对较小，试件横向应力差变小，此时的状态更为接近采取润滑措施的单向荷载。

图11 压力7500kN剪力500kN应力云图

4 结论

通过对混凝土环箍效应的静态应变测量试验和有限元分析，可以得出以下结论：首先，环箍效应真实存在，且对混凝土试块的应变产生不可忽略的影响，通常情况下混凝土试件的实测强度会得到提高，破坏形式也以侧向断裂破坏为主。其次，混凝土破坏主要由垂直于施压方向的最大拉应变造成，三轴受压区域的混凝土受力性能要远远强于同时受拉、压的区域。最后，有约束的单轴受压混凝土试件边缘会出现微元体同时受压、弯(剪)的情况，同时无拉应力，有拉应变。这一区域也是混凝土构件受力情况最不利的位置，在工程实践中应得到及时监测和重点加固。

[1] Lu, D., Wang, G., Du, X., Wang, Y. A nonlinear dynamic uniaxial strength criterion that considers the ultimate dynamic strength of concrete[J].International Journal of Impact Engineering,2017,103:124-137.doi:10.1016/j.ijimpeng.2017.01.011.

[2] Lim, J. C., Ozbakkaloglu, T., Gholampour, A.,Bennett, T., Sadeghi, R. Finite-Element Modeling of Actively Confined Normal-Strength and High-Strength Concrete under Uniaxial, Biaxial, and Triaxial Compression[J]. Journal of Structural Engineering,2016,142.doi: 10.1061/(ASCE)ST.1943-541X.0001589.

[3] Chen, E., Leung, C. K. Y. Effect of uniaxial strength and fracture parameters of concrete on its biaxial compressive strength[J].Journal of Materials in Civil Engineering, 2014,26.doi:10.1061/(ASCE)MT.1943-5533.0000919.

[4] Bielawski, C. Strength criterion for concrete in a triaxial state of stress[J].Archiwum Inzynierii Ladowej,1987,33:483-497.

[5] Lu, D., Wang, G., Du, X., Wang, Y. A nonlinear dynamic uniaxial strength criterion that considers the ultimate dynamic strength of concrete[J].International Journal of Impact Engineering,2017,103:124-137.doi.

[6] Abdel-Fattah, H., Ahmad, S.H. Behavior of hoop-confined high-strength concrete under axial and shear loads[J].ACI Structural Journal,1989,86:652-659.

[7] L. LAM,S.T. SMITH. Analysis and behaviour of FRP-confined short concrete columns subjected to eccentric loading[J]. Journal of Zhejiang University(Science A:An International Applied Physics & Engineering Journal),2008,01:38-49.

[8] 邹艳红,沈明秀. 环箍连接结构参数化有限元优化设计[J]. 电子测试,2015(19):6-7.

[9] 王炜. 交通工程学[M]. 南京:东南大学出版社, 2002.

[10] 王琼. 钢筋混凝土柱托换的试验研究[D].天津大学,2009.

[11] 陈帅. 混凝土斜方体抗压试验研究[D].天津大学,2012.

杨亦凡(1996～)，男，在读本科，土木工程专业。

张文学(1975～)，工学博士,高级工程师，研究方向为桥梁工程。

TU502+.4

A

[定稿日期]2017-03-22