一种基于TIN的多尺度流域河网提取算法

唐志贤

（中国电子科技集团公司第二十八研究所，江苏 南京 210007）

一种基于TIN的多尺度流域河网提取算法

唐志贤

（中国电子科技集团公司第二十八研究所，江苏 南京 210007）

多尺度水文模拟是水文研究的重要领域，多尺度的流域河网是多尺度水文模拟的基础，而现有基于 TIN提取算法存在河道定义单一、未处理平坦区域及不支持多尺度等不足。提出一种基于 TIN 的多尺度流域河网提取算法，定义谷线河道、重心—重心河道和重心—谷线河道等流域河网特征；利用回溯的方法确定平坦区域三角形的流向，进一步确定平坦区域的河道；定义基于 TIN 数据的汇水面积的概念，用以实现空间多尺度流域河网的提取。设计河网的二叉树拓扑结构和编码方案及算法，用于构建流域河网的空间拓扑结构为水文研究提供接口。研究及实验结果表明，提出的算法提取出的流域河网与地形数据中的实际河网吻合。

流域河网提取；不规则三角网；多尺度；梯度

0 引言

防汛减灾关系国计民生，直接影响国民经济发展和人民生命财产安全，实时精准的水文预报是进行防汛减灾科学决策的前提。随着以物联网[1]、云计算[2]、移动互联网和 RS 技术[3]为基础的智慧水利规划的实施，逐步形成天地一体的水利监测体系，将带来数据采集空间密度和时间频率的飞跃，数据获取的触角将伸向水利领域的方方面面，关系、遥感遥测和高分辨率地形等多源异质的观测数据形成互补与互相校正，实现了水利数据从点到面的转变[4]。水利数据的共享交换进程的推进[5-6]，进一步丰富完善了各级水利部门的数据资源。

水利数据资源的日益丰富，使得基于大数据驱动的精细化洪水预报模型[7]被广泛的采用。水系河网是洪水预报的基础，精细化的水文预报模型需要更高精度的水系河网，现有的数字流域水系河网建模的目的是为水文模拟提供产汇流区域，主要包括水系河网提取和集水区域划分，其中河网的提取是核心和基础。目前水系河网提取最经典的方法是 D8（Deterministic Eight Neighbors）算法[8]，在 3×3 的DEM 格网上，计算中心格网与各相邻格网的坡降，取坡降最大的格网单元为中心格网单元的流出格网单元，该方向即为中心格网的流向。虽然基于规则格网 DEM 的水系河网建模技术较为成熟，但是由于格网 DEM 具有的固定分辨率、规则排列数据点等特性，限制了其对地形表达的灵活性和准确性，同时也给水文分析带来一系列的困难，如伪洼地现象、水流方向计算的不准确、模型参数计算困难等[9]。

相对于格网 DEM 而言，TIN 结构的 DEM 数据具有良好的矢量性，能够更加精确地模拟地形地貌，现有研究主要利用三角形的梯度确定水流方向，进而提取谷线形成水系河网[9-10]，形成的河道较为单一。在进行流向计算时，洼地和平坦区域会带来流向无法计算的问题，对于格网 DEM 典型的解决方法是更改相应区域高程[8]或者制定流域河网出口进行回溯搜索[11-12]，对于 TIN 数据，QU 等[10]提出通过修改 TIN 顶点坐标的方式回避了平坦区域的处理，但是对于高精度的 TIN 数据，将由于三角形数量的巨大而难以实现。

水文尺度问题是当今水文研究的前沿，不同水文尺度对应的水文模拟有着不同的规律和方法[13]。作为水文研究的一部分，流域河网也有着不同的尺度。随着研究尺度不同的变化，河网结构也有所不同，而面向多尺度的基于 TIN 的流域河网提取算法目前还未看到。本文将针对现有方法的不足，提出一种基于 TIN 的多尺度流域河网提取算法，定义谷线河道、重心—重心河道和重心—谷线河道等 3 种河道，采用回溯的方法实现平坦区域河道的提取，定义基于 TIN 的河道汇水面积概念，实现多尺度流域河网的提取。

1 基本理论

1.1 多尺度流域河网的概念

尺度是水文研究的一个热点问题，不同尺度的水文模型有着不同规律。作为水文研究的一部分，流域河网也有着不同的尺度。随着研究尺度不同的变化，河网结构也有所不同，如图 1 所示，对比 a和 b 两图可以发现，b 中小尺度的河网结构具有更多的支流，而 a 中较大尺度与 b 相比，则少了部分支流。实际的河流具有不同的产水区域，按照地表水的产汇流原理，河流中水流量的大小与其产水区域成正比关系。根据产水区域的不同可以生成不同流域河网，如图 1 b 的部分支流的产水区域的面积（即汇水面积）小于图 1 a 的要求，故在图 1 a 中的流域河网只有图 1 b 中的一部分，这部分具有较大的汇水面积。按照上述分析，利用不同的汇水面积可以构建不同尺度的流域河网，为此将传统格网 DEM 流域河网提取中汇水面积的概念引入到 TIN 流域河网提取中，根据不同的汇水面积生成不同尺度的流域河网，以实现多尺度流域河网的提取。

1.2 基于 TIN 的流向分析

TIN 数据中三角形水流方向的确定是基于 TIN的流域河网提取的关键和基础。确定 TIN 水流方向的思路是：利用几何原理，求解出 TIN 中空间三角形的梯度向量，进一步求解出 TIN 的水流方向，对于无法通过几何性质求解水流方向的三角形（平坦区域），采用回溯的方法予以确定。

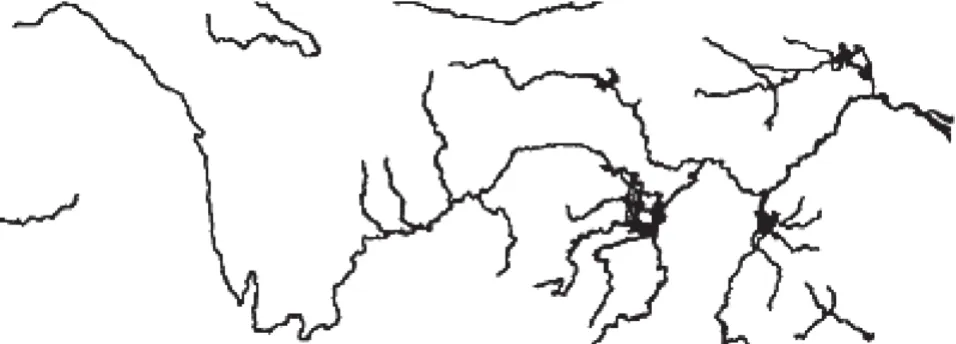
a 国家级尺度的长江流域河网

图 1 不同尺度的流域河网

1.2.1 TIN 的水流方向确定

根据数学原理，TIN 中空间三角形的梯度是地形最陡峭的方向，是高程值上升最快的方向，其反方向将是高程值下降最快的方向，地表水是在重力的作用下流动的，而此可以认为，水是沿着地表梯度的反方向流动的，即 TIN 中空间三角形的水流方向为空间三角形梯度的反方向。设空间三角形的 3 个顶点坐标为 A (xa，ya，za)，B (xb，yb，zb)，C (xc，yc，zc)，则该空间三角形的梯度为：

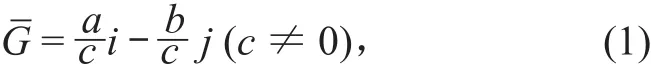
则空间三角形的水流方向为：

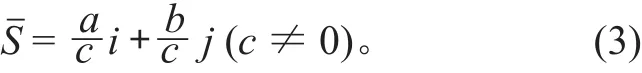
在已知方向的情况下，要唯一确定 1 个向量，只需要该向量上的 1 点。由于论文研究的是空间三角形的水流方向，水是在重力的作用下流动，本文选择经过空间三角形 ΔABC 的重心点 O (xo，yo，zo)的向量作为 ΔABC 的水流方向向量，称其为 ΔABC的流向向量，如图 2 所示。设空间三角形 ΔABC 的3 个顶点分别为：A (xa，ya，za)，B (xb，yb，zb)，C (xc，yc，zc)，则该三角形的重心 O (xo，yo，co) 为：

特别地，为了更加精确地表示水流方向，将以△ABC重心为起点，方向为向量的射线定义为水流方向。

图 2 空间三角形的流向向量

式（1）～（4）要求参数c≠ 0，若c= 0 则空间三角形的 3 个顶点在统一水平面，即 3 个顶点的高程值相等，这属于 TIN 中的平坦区域。平坦区域的空间三角形无法求导数，从而无法求出该三角形的水流方向向量，本文将采用从流域出口进行回溯方法以解决平坦区域流向计算问题。

1.2.2 空间三角形边的特征线分析

图 3 流向向量与边的关系

2 河道提取

为了解决现有方法河道单一的问题，定义了 3 种河道：重心—重心河道、谷线河道、重心—谷线河道；其中重心—重心河道针对非谷线三角形，谷线河道、重心—谷线河道针对谷线三角形。为此针对谷线和非谷线 2 类不同三角形，设计了不同的河道提取算法。

图 4 相邻三角形公共边的分类

对于非谷线三角形 ΔABC的流向向量所指三角形为 ΔABC′，这样连接 ΔABC的重心O(xo，yo，zo)和 ΔABC′的重心O′(x′o，y′o，z′o)，就形成了 ΔABC和 ΔABC′间的简单河道，记为重心—重心河道，如图 5 所示。若 ΔABC的流出三角形将不唯一（此时流向向量与边的交点落在三角形的顶点上，这样会有 2 个流出三角形），算法选择重心较低的那个三角形作为 ΔABC流出三角形。

对于谷线三角形，若直接连接重心形成河道，水将在这 2 个三角形间循环，设计了重心—谷线河道与谷线河道，如图 6 中OLIL和ORIR所示。提取算法流程如图 7 所示，若三角形T含有 2 条谷线Ei，Ej，则与Ei，Ej有且只有 1 个交点PI，连接T的重心OT与PI形成河道； 若三角形T只含有 1 条谷线Ei，则进一步分析与Ei（含延长线）的相交关系；若与Ei直接相交（交点记为PI）连接T的重心OT与PI形成河道，若与Ei的延长线相交，设距离交点PI较近Ei的端点为PE，连接T的重心OT与PE形成河道。在三角形T只含有 1 条谷线Ei且与Ei的延长线相交的情况下，由于的方向是高程较低处，PE一定是Ei高程较低的端点，故连接OT与PE形成河道是合理的。对于谷线，认为其构成河道，记为谷线河道（如图 6 中ILIR所示）。

图 5 重心-重心河道

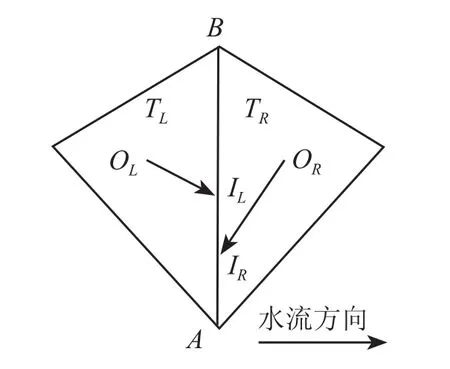
图 6 谷线三角形中的河道

3 平坦区域的处理

图 7 河道提取流程图

产生平坦区域的原因很多，有的是真实地形的表现（例如湖泊地区），有的是由于采样精度的原因，构成三角形的 3 个顶点在同一水平面，而三角形内部的高程值与顶点不相等。TIN 数据中的平坦区域表现为 TIN 数据中空间三角形 3 个顶点的高程值相等。由于平坦区域空间三角形的顶点高程值相等，三角形平面内所有点的导数均为 0，从而无法计算水流方向FD利进而无法进行提取河道提取。对TIN 数据结构的平坦区域，从流域出口进行回溯的处理方法如算法 1 所示：从流域出口进行回溯，遍历流域出口点的相邻的三角形，若有方向没有确定的，则设置其流出三角形为流域出口三角形，依次回溯上去。如图 8 所示，对于当前处理三角形T相邻三角形T2为平坦区域三角形，按照算法思想，设置T2的流出三角形为T，连接T2重心到T重心形成河道。

算法 1 平台区域处理算法

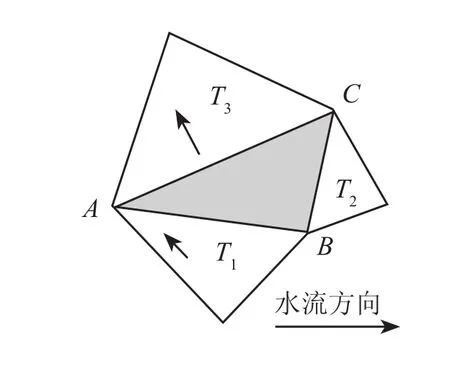
a 平坦区域回溯前的流向

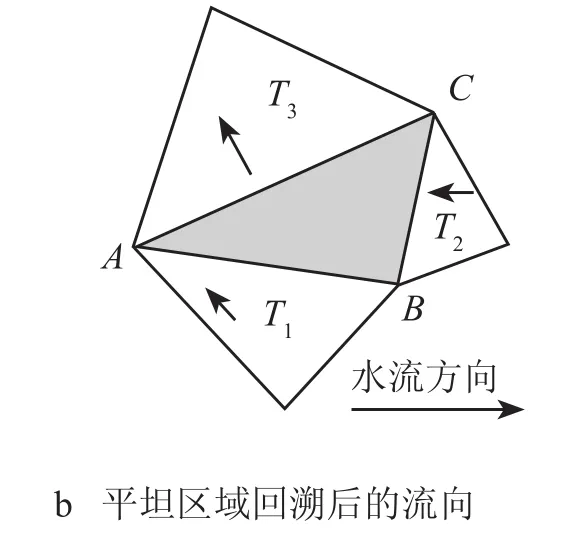
图 8 平坦区域的回溯处理

4 多尺度流域河网的生成

实际的河流具有不同的产水区域，按照地表水的产汇流原理，河流中水流量的大小与其产水区域成正比关系。根据产水区域的不同可以生成不同流域河网。根据产汇流原理，河道的汇水面积取决于其经过区域的面积，本文将从分析 TIN 数据中空间三角形的汇水面积入手，逐步定义河道的汇水面积，进而实现多尺度流域河网的生成。

4.1 TIN 数据中空间三角形汇水面积分析

算法认为每个三角形的产水量与其面积成正比，不妨设空间三角形T的产水量为其面积ST，其汇水面积则等于该三角形的流入三角形的汇水面积之和加上其产水量，如果该三角形没有流入三角形，则其汇水面积就为该三角形的面积。设三角形ΔABC的相邻三角形T1，T2，T3的汇水面积分别为A1，A2，A3，则 ΔABC的汇水面积：

式中：1 ≤i≤ 3，Ti的流出三角形为T。

4.2 河道汇水面积分析

在分析 TIN 数据中空间三角形汇水面积的基础上，进一步确定河道的汇水面积。对于非谷线河道，论文采用的思想是：以其起点所在三角形的汇水面积为该河道的汇水面积，这里也分 2 种情况：1）直接连接 2 个三角形重心的河道，即重心—重心河道（图 9 a）；2）从三角形重心出发到谷线的河道，即重心—谷线河道（图 9 b）。对于重心—重心河道，如图 9 a 所示，设其起点为三角形T的重心O，终点为三角形T1的重心O1，则河道OO1的汇水面积：Aoo1=AT，对于重心—谷线河道ORIR的汇水面积=ATR（图 9 b）。对于谷线河道，其汇水面积等连接到该谷线河道的重心—谷线河道汇水面积之和，即其左右三角形的汇水面积，如图 9 b 中的AB河道，其汇水面积：

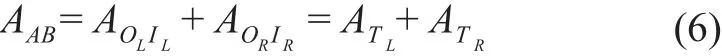
图 9 河道汇水面积的计算

4.3 多尺度流域河网的拓扑结构分析

流域河网提取的实质是将离散的河道按照设计的空间拓扑结构结合起来形成一个整体，故设计一套合理的流域河网空间拓扑结构是至关重要的。在研究现有河网流域拓扑结构的基础上，结合 TIN 数据结构，采用如图 10 所示的二叉树结构描述流域河网空间拓扑结构。树型流域河网拓扑结构采用以下基本结构描述流域河网空间拓扑结构：

1）河流源点。河流源点是河流发源点，是流域河网生成时汇水面积正好等于阈值的节点，1 个流域有多个河流源点。

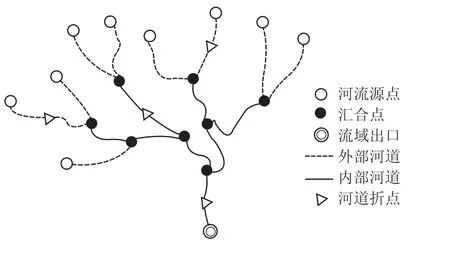
图 10 多尺度流域河网拓扑结构

2）汇合点。汇合点是不同支流汇合的地方，是流域河网生成时同时有 2 个河道流入的那些格网，对于 1 个流域河网不存在 2 条以上的支流在同一地点汇合。

3）河道。即河流，河道分为内部和外部河道，外部河道是河流源点与汇合点之间河流，内部河道则是除外部河道之外的河流。

4）流域出口。整个流域的最下游，1 个流域一般只有 1 个流域出口。流域出口是一个很重要流域属性，对平坦区域处理时需要从流域出口开始回溯。

5）河道折点。1 个三角形含有 2 条谷线边时，这 2 条边的交点边便是河道折点，河道折点是唯一一条河道起点且只是另一条河道的终点。

在 5 种基本结构中，汇合点主要有 2 种情况：1）三角形 T 的重心，该三角形有 2 个相邻三角形Ti，Tj的水流流入该三角形，河道则由流出三角形的重心到 T 的重心构成；2）谷线上的点 P，分为水流向量与谷线直接相交的交点，或者谷线较低端点，河道由三角形重心到点 P 的连线构成。

对于河道集合中的河道 REi，若其起点 Psi不再是其它河道的起点，则点 Psi就是河流源点，则河道REi为外部河道。若 Psi是另外某条河道的终点且 Ei的终点 Pei同时是 2 条河道的终点，则河道 REi是内部河道。若 Pei不是任何河道的起点，则 Pei是为流域出口。需要说明的是基于本文设计的河网结构，内部河道的端点都是汇合点。若河道 REi的端点 Pi只是某一条河道起点且只是另一条河道的终点，则 Pi为河道折点。

通过汇水面积阈值来过滤部分河道，认为汇水面积大于汇水面积阈值的河道才能形成河网。由汇水面积的计算过程可以发现河道的汇水面积是该河道的产水区域的面积，因此，通过汇水阈值设置的不同，变可以动态的生成不同尺度的流域河网，以满足水文研究对不同尺度的要求。

5 案例研究

为了验证算法的可行性与性能，本文将利用沿渡河流域的 4 组 TIN 数据进行实验，表 1 给出了实验数据的基本参数，通过对表 1 进行分析，从数据量来看，第 1 组和第 2 组数据量较小（三角形和边的数目相对较小），第 3 组和第 4 组数据量较大（三角形和边的数目相对较大）。从高程值角度来看，第 2 组的高程值变化较为剧烈，其余 3 组高程变化不大，具有平坦区域。总体上 4 组实验数据比较典型，能够较为全面的测试算法的可行性与性能。本文以第 4 组实验数据（如图 11 所示）为例进行分析。

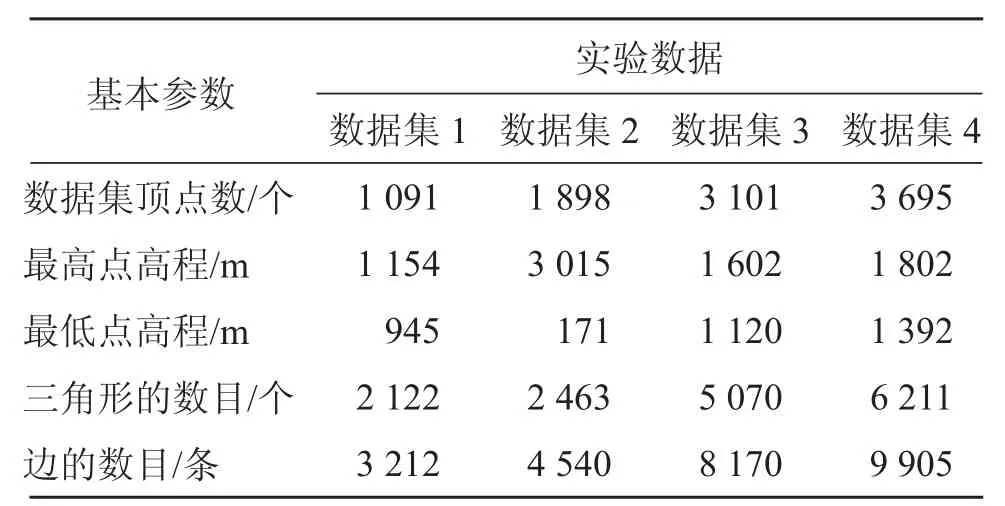
表 1 实验数据基本参数

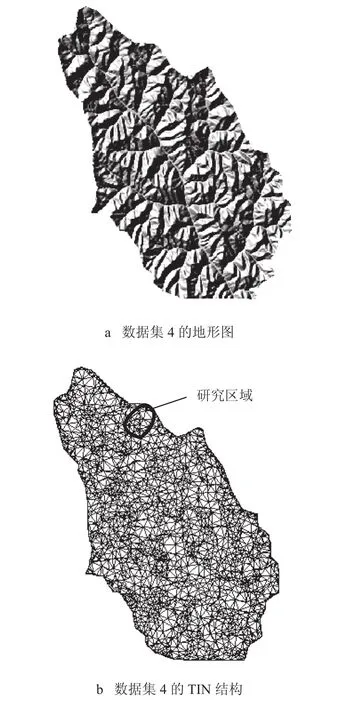
图 11 数据集 4 示意图

针对表 1 所列实验数据，利用实验平台进行了实验。对于第 4 组数据，如图 12 a 所示为提取重心—重心河道的提取结果效果图，由于还未对谷线三角形进行河道提取，造成很多重心—重心河道是分离且不连续的（图 12 a 中的河道 AB），这是因为还没有对谷线三角形进行河道提取，图 12 b 是对谷线三角形进行河道提取后的效果图。从图 12 b 可以发现，在处理了谷线三角形后，形成的重心—谷线河道 BE 将重心—重心河道 AB 与谷线连接起来，从而将分离的河道相互连通。在图 12 a 和图 12 b 中的三角形 T，它既不是谷线三角形，也没有重心—重心河道，这是因为其 3 个顶点的高程相等，重心处梯度为零，流向不存在，需要通过回溯确定流向，进而提取河道。如图 12 c 所示在对选定的实验数据进行回溯的过程中，在回溯到三角形 T1时确定三角形 T的流向，提取出重心—重心河道 FG。其中图 12 中的 TIN 数据边是指 TIN 数据中空间三角形的边。

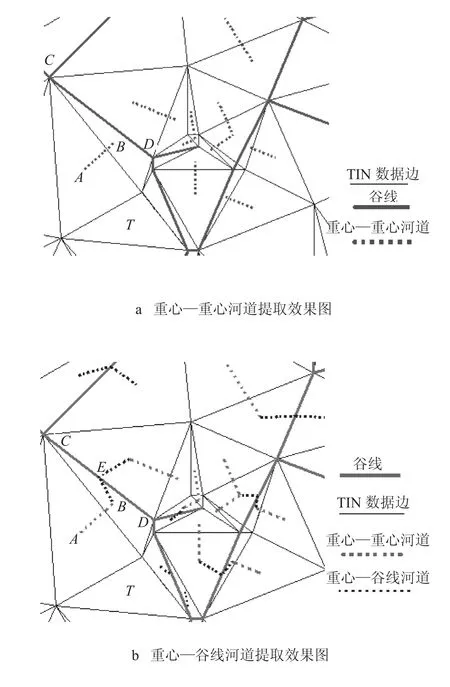
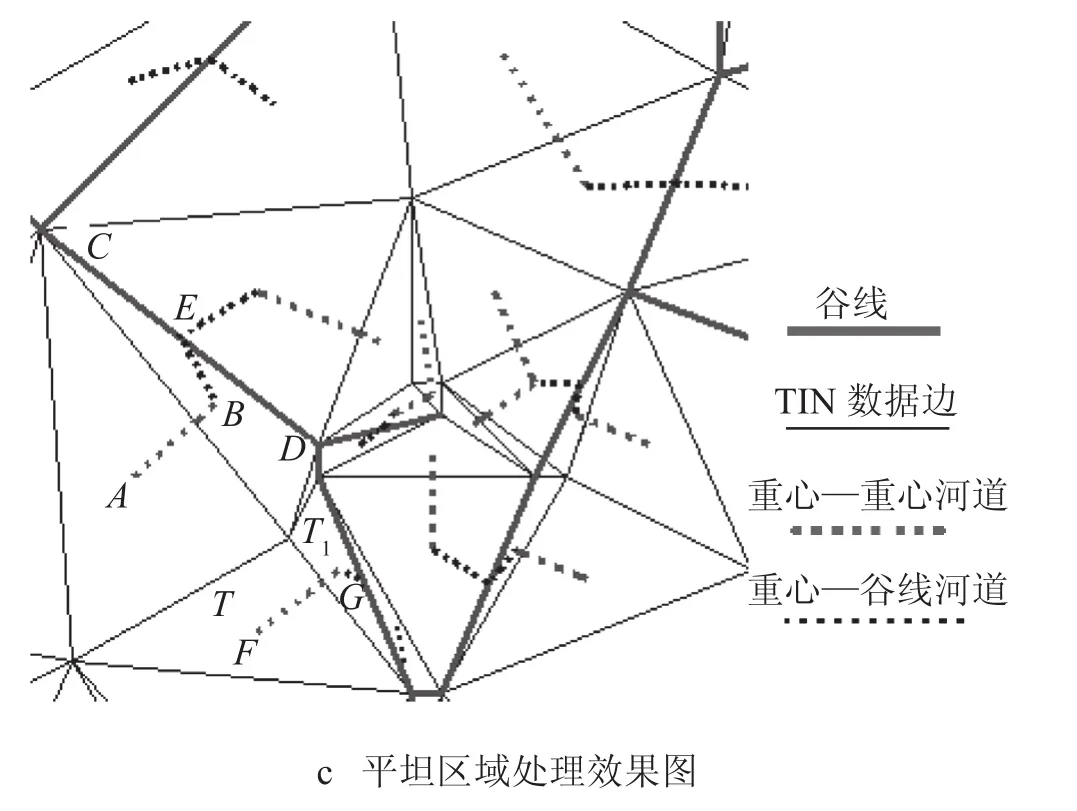
图 12 河道提取示意图

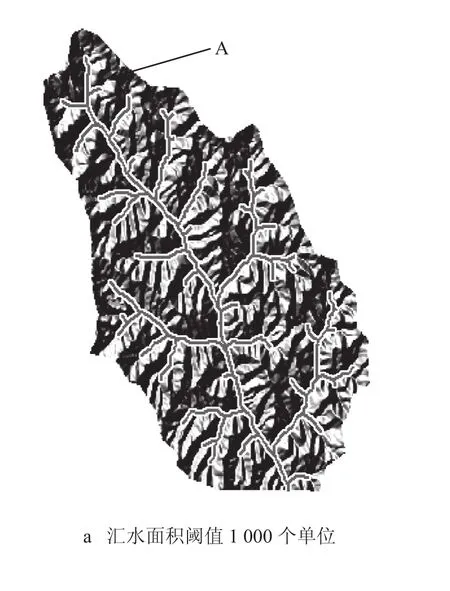
图 13 给出了图 11 中实验数据的不同尺度流域河网提取结果，通过对比 a 与 b 可以发现，当汇水阈值变大后，图 13 a 中部分河道（例如图 13 a 中的 A部分）的汇水面积小于汇水阈值，将不再是河网的一部分，实现了河网的多尺度提取。实验表明，本文提出的算法能够实现从 TIN 数据中进行河网的提取，并可以通过设置汇水面积阈值实现动态生成不同尺度的流域河网，且实验结果与原始地形相吻合。

表 2 列出了实验数据的概况与进行相关操作所需的时间（CPU P4 3.2 GB，内存 2 GB）。其中，为了算法实现的方便，河道提取时间包括了谷线和非谷线三角形的时间，汇水面积计算时间包括三角形与河道的汇水面积的计算时间，河网构建时间包括河网结构信息提取、分级与编码的时间，流域河网提取时间是算方法各个部分的时间总和。通过分析表 2 可以发现，提出多尺度流域河网提取算法的是线性时间复杂度。

图 13 数据集 4 示意图与实验结果图

表 2 算法运行时间分析

6 结语

提出了一套基于 TIN 的多尺度流域河网提取算法，在利用空间三角形重心处导数这一几何性质计算流向的基础上，定义了基于 TIN 的重心—谷线河道、重心—重心河道等 3 种河道，采用从流域出口进行回溯的方法处理平坦区域，定义了基于 TIN 的汇水面积和多尺度的流域河网结构以实现多尺度流域河网的提取，经过实验验证本文提出的提取算法是可行的。下一步工作可以考虑采用借助 DLRN 提取的河道“蓝线”提高回溯精确度，或者借助神经网络确定流向；对于有 2 个以上连通分支的河网的提取还需要作进一步研究，可以在进行 TIN数据分割的基础上再进行河网提取。

[1] 倪建军，汤敏，詹万林，等. 水联网与水利信息化理论探讨及应用实践[J]. 水利信息化，2016 (4): 32-35.

[2] 朱跃龙. 水利信息化与云计算[J]. 水利水电技术，2013 (1): 7-11.

[3] 董静. 遥感技术在水利信息化中的应用综述[J]. 水利信息化，2015 (1): 37-41.

[4] 冯钧，许潇，唐志贤，等. 水利大数据及其资源化研究[J]. 水利信息化，2013 (4): 6-9.

[5] 冯钧，唐志贤，盛震宇，等. 水利数据中心数据交换平台设计探讨[J]. 水利信息化，2014 (1): 15-19.

[6] 成建国，冯钧，杨鹏，等. 水利数据资源目录服务关键技术研究[J]. 水利信息化，2014 (6)： 18-21，35.

[7] LI Z, XIN P, TANG J. Study of the Xinanjiang model parameter calibration [J]. Journal of Hydrologic Engineering, 2013, 18 (11): 1513-1522.

[8] MORAN C J, VEZINA G. Visualizing soil surfaces and crop residues [J]. IEEE Computer Graphics and Applications, 1993, 13 (2): 40-47.

[9] 刘学军，王永君，任政，等. 基于不规则三角网的河网提取算法 [J]. 水利学报，2008，39 (1): 27-34.

[10] QU G D, SU D Y, LOU Z H. A new algorithm to automatically extract the drainage networks and catchments based on triangulation irregular network digital elevation model [J]. Journal of Shanghai Jiaotong University(Science), 2014, 19 (3): 367-377.

[11] HOU K, YANG W, SUN J, et al. A method for extracting drainage networks with heuristic information from digital elevation models [J]. Water Science and Technology, 2011, 64 (11): 2316-2324.

[12] HOU K, SUN J, YANG W, et al. Automatic extraction of drainage networks from DEMs base on heuristic search [J]. Journal of Software, 2011, 6 (8): 1611-1618.

[13] 戚晓明，陆桂华，金君良. 水文尺度与水文模拟关系研究[J]. 中国农村水利水电，2006 (11): 28-31.

Research on algorithm for extracting multi-scale drainage network based on TIN

TANG Zhixian
(No.28 Research Institute, China Electronics Technology Group Corporation, Nanjing 210007, China)

Multi-scale hydrologic modeling is an important area of hydrological research. Multi-scale river basin is the basis of multi-scale hydrological modeling. While existing extraction algorithm which based on TIN has some shortages such as the de fi nition of river singly, treating only for non- fl at areas and un-supporting for multi-scale river basin. This thesis presents a method for extracting multi-scale drainage network based on TIN, de fi nes some features of river basin such as the line, the river valley, the center of gravity - the center of gravity and center of gravity river -the river valley line; determines the fl ow of the triangular fl at areas by using the method of fl at back, then determines the river of fl at areas further; introduces the concept of watershed area based on TIN to extract multi-scale drainage network. It proposes a binary tree topology with a coding schema to represent the drainage network, providing interfaces for digital hydrology research. The result indicates that the drainage network extracted by this method is basically consistent with the actual river.

drainage extracting; TIN; multi-scale; gradient

P333

A

1674-9405(2017)04-0028-08

10.19364/j.1674-9405.2017.04.006

2017-06-26

国家自然科学基金项目（61370091）

唐志贤（1983-），男，四川遂宁人，博士，研究方向：数据管理与知识工程。