基于抗裂要求的楼面梁预应力筋数量及其影响因素探讨

徐建设

(上海理工大学 环境与建筑学院,上海 200093)

基于抗裂要求的楼面梁预应力筋数量及其影响因素探讨

徐建设

(上海理工大学 环境与建筑学院,上海 200093)

在房屋建筑结构的楼面预应力梁设计中,一般需要先行估算预应力筋的数量,传统的基于经验的估算方法往往误差较大.对满足各级抗裂要求所需的预应力筋数量进行了研究.首先列出3种抗裂等级所对应的预应力筋数量的表达公式,引入合理假定后,得到预应力梁跨中和支座处所需预应力筋数量的简化计算公式.之后对预应力筋数量的各种影响因素(梁截面形状、梁跨度、梁截面宽度、抗裂等级、板厚、预应力筋位置等)分别进行了讨论,得出了预应力筋数量与各因素的关系曲线,再将各因素对预应力筋数量的影响程度进行了比较,为结构设计人员在初步设计阶段估算预应力筋数量提供了一种较为准确的依据.

预应力梁; 预应力筋数量; 抗裂

在房屋建筑结构中,当楼面跨度较大时,采用预应力梁可有效降低梁高、增加楼面刚度、改善抗裂性能.增加预应力筋的数量,提高预应力配筋率，可以增加预应力梁的开裂荷载[1].在预应力楼面结构设计中,一个重要的步骤是确定预应力筋的形状及其合理数量,这将直接影响结构的承载力、抗裂性能以及经济性等指标.对于预应力筋的形状,设计人员易通过弯矩图的特点选用抛物线或其他合理线形,但是，对于预应力筋的数量,目前的方法一般是，设计人员首先根据经验估算出预应力钢筋的根数,之后进行承载力及抗裂等验算.如果不满足要求或过于保守,则需要重新调整预应力筋的数量.估算的预应力筋数量是否合理,取决于预应力设计人员的经验.由于我国大多数设计单位并未普及预应力结构的设计,在初步设计阶段,有些设计人员往往根据一些没有充分依据的经验估计预应力筋的数量,比如“每米一根(即预应力筋的根数约等于跨度)”或“每根钢绞线相当于一根25的钢筋(即直接用一根钢绞线替代一根25的钢筋)”等.这些所谓的经验之谈往往误差较大,使得后期需要反复调整,加大了验算的工作量,不利于初学者对于预应力结构的掌握,也间接影响了预应力结构在设计单位的普及.

针对上述情况,本文以建筑结构的预应力楼面梁为研究对象,直接给出预应力筋数量的估算公式,然后通过对预应力筋数量的影响因素进行分析,讨论各因素对预应力筋数量的影响大小.有助于在初步设计阶段确定预应力的合理数量,使得预应力结构的设计能够顺利进行.

1 预应力筋数量的两种估算方法

1.1 平衡荷载法

平衡荷载法[2]于1961年由林同炎教授提出,是一种非常方便和巧妙的计算工具，其原理是将预应力的作用视为一种荷载(称为平衡荷载),平衡荷载的方向与外荷载相反.图1为承受均布荷载的简支梁受力简图,其恒荷载、活载分别为gk和qk,抛物线矢高为e1,梁跨度为l.根据不同的设计要求,平衡荷载q的大小可初步选定为(gk+qk)/2或gk,前者平衡掉一半的竖向荷载,后者平衡掉全部恒载.

然后估算预应力Np.

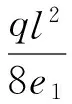
(1)

由式(1)可以确定预应力筋的根数

(2)

式中，Np1为单根预应力筋的预拉力值,为单根预应力筋的面积Ap1与有效预应力σpe的乘积.

按式(2)估算预应力筋的数量非常简单、易用、概念清晰,但是，由此得出的预应力筋根数仅能保证有多少外荷载被“平衡”掉,未考虑具体抗裂等级的要求,难以保证构件能满足下一步的抗裂及承载力验算要求.

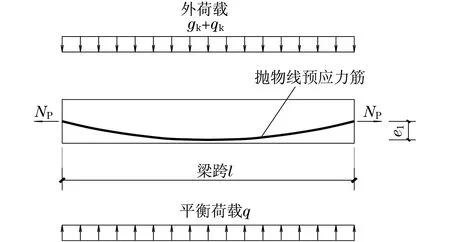
图1 简支梁的平衡荷载Fig.1 Balanced load of simply supported beam

1.2 抗裂要求法

根据不同的裂缝等级要求进行计算.对于一级抗裂,其要求为

(3)

式中:σck为构件截面边缘混凝土的法向应力;σpc为截面的预压应力;Mkmax为截面最大弯矩标准值;W为截面抵抗矩;Npe为有效预应力的合力;A为截面面积;e为预应力合力点至截面形心的距离.

由式(3)可得

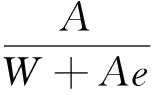
(4)

考虑到

Npe=nσpeAp1

(5)

可得一级抗裂的预应力筋根数要求为

(6)

对于二级抗裂,其要求为

(7)

式中，ftk为混凝土的抗拉强度标准值.

由式(7)及式(5)可得二级抗裂相应的预应力筋数量要求为

(8)

对于三级抗裂,较为准确的计算方法是根据GB50010[3]的裂缝宽度计算公式,即按照荷载效应的标准组合并考虑长期作用影响计算裂缝宽度,但采用该公式计算裂缝宽度较为复杂,一般用于施工图阶段的裂缝验算.在结构方案或初步设计阶段,可采用较为简单的名义应力法[4-5],将允许最大裂缝宽度与相应的混凝土截面边缘名义弹性拉应力限值[σct1]之间建立联系.由文献[4],其抗裂计算公式为

(9)

其中,[σct1]的取值如表1所示,表中数值尚应根据梁截面高度乘以相应的修正系数.

表1 混凝土名义拉应力限值Tab.1 Limit value of the allowable nominal tensile stress of concrete N/mm2

由式(9)及式(5)可得三级抗裂相应的预应力筋数量要求为

(10)

2 预应力筋数量的影响因素

由于平衡荷载法得到的预应力筋数量过于粗糙,现以抗裂要求法为例,研究预应力梁的预应力筋数量的影响因素.

2.1 预应力筋数量计算的简化假定

对于一至三级抗裂的预应力梁,其抗裂所需的预应力筋数量分别如式(6),(8),(10)所示,现对预应力梁作如下假定:

a. 预应力筋为目前国内工程中最常用的1 860级φ15.24 mm钢绞线(fptk=1 860 N/mm2),单根预应力筋的面积Ap1=140 mm2.

b. 预应力筋张拉控制应力σcon取0.7fptk,即1 302 N/mm2.有效预应力σPe按0.8σcon估算(即预应力总损失按0.2σcon估算),因而σpe=0.8×1 302=1 042 N/mm2.

c. 梁截面弯矩Mmax由经验系数法进行估算.梁的跨中弯矩Mmax1和端部弯矩Mmax2分别为

Mmax1=α(gk+qk)l2,Mmax2=β(gk+qk)l2

式中:α和β为经验系数,其取值按照美国UBC[6]介绍的经验系数,如表2所示.

表2 弯矩系数表Tab.2 Moment coefficient table

d. 梁的截面抵抗矩W和预应力筋偏心距e分两种截面考虑,对于矩形截面(图2(a))和T形截面(图2(b)),其W和e的取值可以统一表示为

(11)

(12)

式中:a1,a2分别表示预应力筋形心至梁底面和顶面的距离.

对于矩形截面,式(11)和式(12)中截面惯性矩I取bh3/12,y1和y2取值均为h/2.

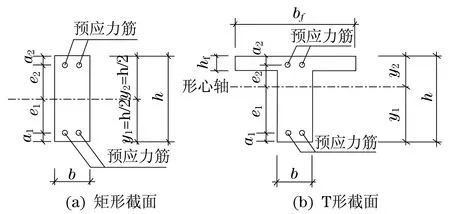
图2 矩形和T截面特性Fig.2 Characteristic of rectangle and T shape section

2.2 预应力筋数量的简化计算公式

式(6),(8),(10)可统一表达为

(13)

其中

(14)

将Ap1,σpe,Mmax的简化公式以及式(11)和式(12)带入式(13),得

(15)

其中,α和β的取值见表2.式(15)即为各级抗裂等级下楼面预应力梁跨中及支座截面所需预应力筋数量的简化计算公式.

2.3 预应力筋数量的影响因素

由式(14)和式(15)可知,影响梁预应力筋数量的因素有:

a. 荷载大小(gk+qk);

b. 截面位置(影响α和β的取值);

c. 梁跨度(l);

d. 抗裂等级;

e. 梁的截面特性(A、I、y1、y2)

f. 预应力筋位置,即预应力筋形心至梁截面边缘(顶面或底面)的距离(a1、a2);

3 预应力筋数量与各影响因素的关系

在各影响因素中,荷载大小、截面位置(外支座、内支座、中跨跨中、边跨跨中)、混凝土强度等级等与预应力筋数量的关系较为直接,判定较为容易.现对其他因素进行探讨,包括梁的跨度、抗裂等级、截面特性、预应力筋位置等,其中,梁的截面特性与梁的截面形状(矩形或T形)、截面宽度、截面高度、板厚(板厚影响T形截面的特性)等均相关,但是,由于梁的截面高度一般与跨度呈线性关系,因而不再对梁截面高度进行单独讨论.

3.1 预应力筋数量与梁跨度的关系

先考虑一级抗裂的情况,对于常用的预应力梁跨度范围(现取8～22 m),假定梁高度为跨度的1/15,梁截面宽度为400,板厚150,恒载和活载标准值均为30 kN/m,则按照式(15)得到的梁各位置所需预应力筋数量如图3和图4所示.图3按照矩形截面计算,图4按照T形截面计算.图中一级表示抗裂等级为一级.

图3 n与l的关系(一级,矩形截面)Fig.3 Relationship between n and l (grade 1,rectangle)

图4 n与l的关系(一级,T形截面)Fig.4 Relationship between n and l (grade 1,T shape)

由图3和图4可知,对于一级抗裂等级的预应力梁,采用矩形截面计算时,预应力筋数量(以下简称n)随跨度的增加而逐渐增大,基本与跨度呈线性关系.采用T形截面计算时,跨中截面的n与上述规律相同,但支座截面的n在梁跨较小时随跨度的增加而略有降低,但随后基本与跨度呈线性增大.此外,由图可知,梁各截面所需的预应力筋数量n相差较大,内支座n最大,跨中n最小.与“每米一根法”相比较,除内支座外,各截面的n基本小于按照“每米一根法”确定的预应力数量,且跨度越大,“每米一根法”的误差也越大,表明该估算方法的参考意义并不大.

二级和三级抗裂的计算结果如图5～8所示,其中三级抗裂的允许裂缝宽度按0.1 mm考虑.可以看出,n随跨度的变化规律与一级抗裂等级的情况类似,且按照“每米一根”的方法估算的n误差也很大.

图5 n与l的关系(二级,矩形截面)Fig.5 Relationship between n and l (grade 2,rectangle)

图6 n与l的关系(二级,T形截面)Fig.6 Relationship between n and l (grade 2,T shape)

3.2 预应力筋数量与抗裂等级的关系

取内支座截面进行比较,其n与抗裂等级的关系如图9所示(图中选取了梁跨分别为8～20 m的4种情况).

由图9可知,对于各种跨度的梁,n由一级至三级依次减少,且减少的幅度差异不大.对于本算例的情况,n由一级至二级约减少10%,由二级至三级再减少10%.其他位置截面的规律同上述规律类似.

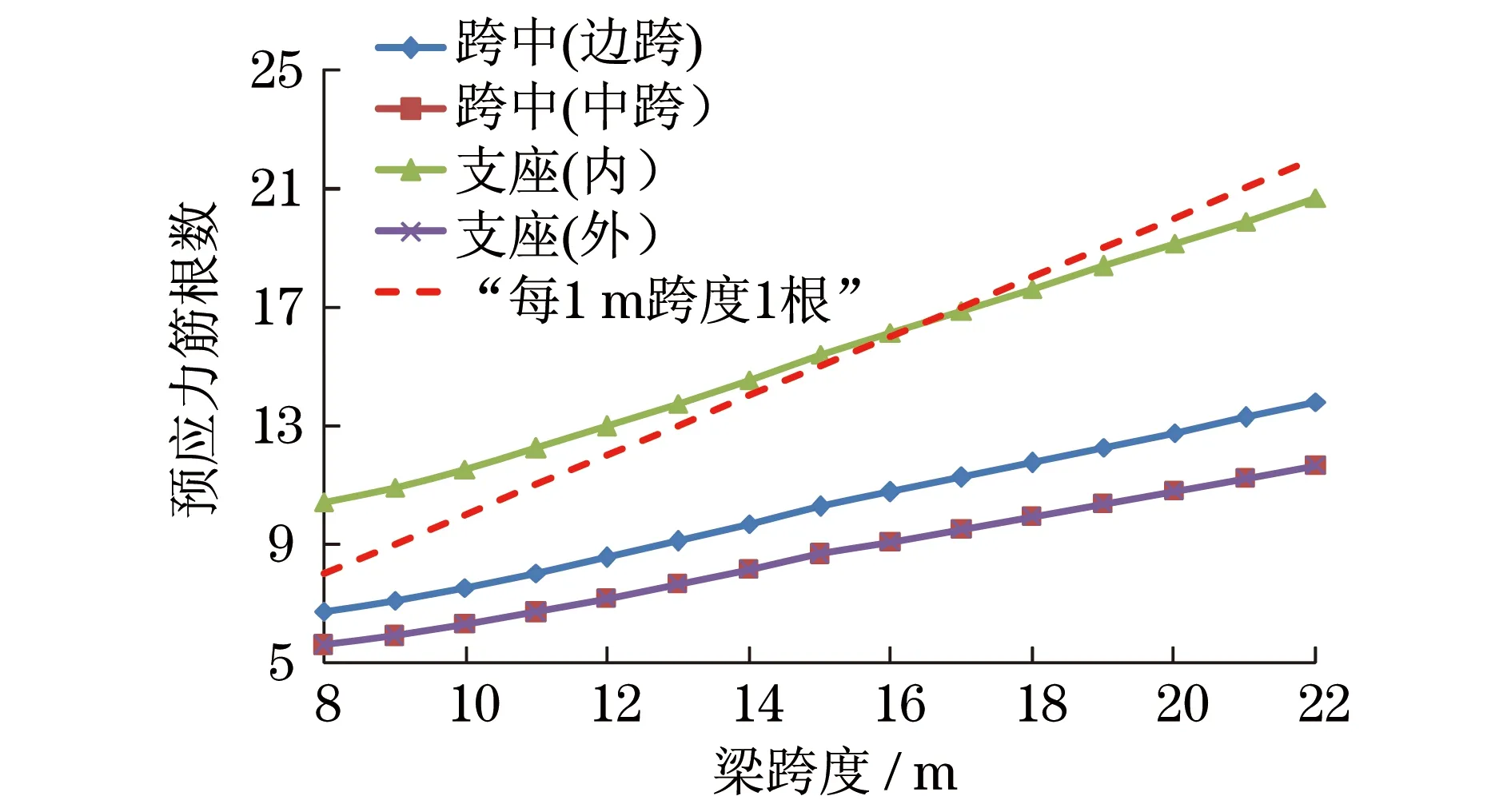
图7 n与l的关系(三级,矩形截面)Fig.7 Relationship between n and l (grade 3,rectangle)

图8 n与l的关系(三级,T形截面)Fig.8 Relationship between n and l (grade 3,T shape)

图9 各抗裂等级的n比较Fig.9 Comparison of value n for various crack resistance grades

3.3 预应力筋数量与截面形状的关系

仍以内支座截面为例进行比较,矩形和T形截面的n随梁跨度的变化情况如图10所示,图10中仅示出了二级抗裂的情况.

由图10可知,在大部分跨度范围内,内支座截面按T形截面计算的n小于按矩形截面的n,只有当跨度较小时会出现相反的情况.其原因是由于跨度较小时,梁高也相应较小,T形截面的翼缘部分所占面积的比例较大,即T形截面相对于矩形截面而言,其面积增加较多,而截面抵抗矩(即I/y2)的增加相对较少,由式(15)可知,其结果会使得T形截面的n大于矩形截面的.随着跨度的增加,梁高逐渐增大,T形截面的截面抵抗矩相对于矩形截面的增加幅度超出截面面积的增加幅度,因而T形截面的n会小于矩形截面的.

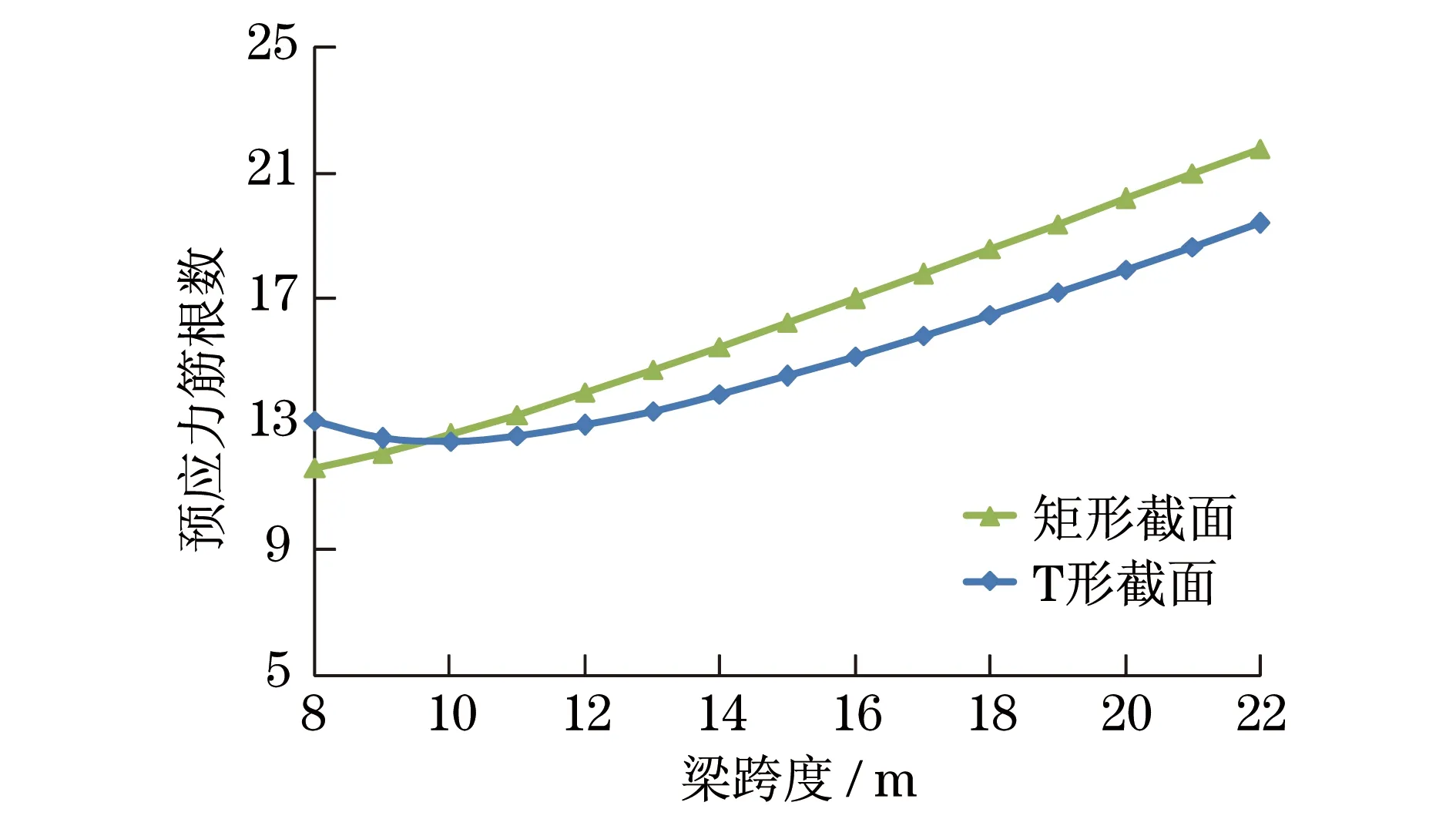
图10 矩形和T形截面的n比较Fig.10 Comparison of n for rectangle and T shape sections

对于其他位置的截面,由计算可知,采用T形截面算得的n一般小于采用矩形截面的n.

3.4 预应力筋数量与截面宽度的关系

仅研究内支座截面.对于一级抗裂等级,在其他因素不变的情况下,n与截面宽度的关系如图11所示.

图11 n与截面宽度的关系(一级)Fig.11 Relationship between n and section width (grade 1)

显然,对于一级抗裂,按矩形截面计算时,n值与截面宽度b无关.其原因在于,矩形截面的面积和截面抵抗矩均与其截面宽度成正比,使得按式(15)算得的n保持不变.按照T形截面计算时,n随b的增加而缓慢减少.这表明对于一级抗裂等级,增加梁宽并不能有效减小预应力的配筋量.

二级抗裂的计算结果如图12所示.n随b的增加而减小,但并不显著(梁宽增加至原来的3倍时,n仅减小约20%).三级抗裂时n随b的变化规律与二级抗裂的情况类似.

图12 n与截面宽度的关系(二级)Fig.12 Relationship between n and section width (grade 2)

3.5 预应力筋数量与T形截面翼缘板厚的关系

按照T形截面计算时,由于翼缘板厚度hf对截面特性的影响较大,进而影响n.以内支座截面为例,各抗裂等级的n随hf的变化规律如图13所示.显然,三种抗裂等级的n随hf的变化规律差异悬殊.对于一级抗裂,n随hf的增大明显增加.二级抗裂时,n随hf的增大呈现先减小后增大的趋势.三级抗裂时,n随hf的增大而明显减小.其原因在于,对于一级抗裂,式(15)的ftt项为0,随着hf的增加,截面抵抗矩和截面面积都增加,但截面形心距梁顶的距离y2不断减小,因而算得的n随hf的增大而增大.对于三级抗裂的情况,式(15)的ftt项较大,随着hf的增大,截面抵抗矩(即I/y2)与ftt的乘积增加较快,因而算得的n随hf的增大而减小.抗裂等级二级的情况介于一级和三级之间,呈现先减小后增大的趋势.

图13 n与hf的关系(一级)Fig.13 Relationship between n and hf (grade 1)

3.6 预应力筋数量与预应力筋位置的关系

预应力筋位置用预应力筋形心至梁截面边缘(顶面或底面)的距离(a1或a2)表示.如下页图14所示(图中规律适用于各种抗裂等级),在其他因素不变的情况下,n随a1或a2的增大而增加,增加的幅度开始较为缓慢,但当a1或a2超过200 mm后,增加幅度有加快的趋势.这是由于a1或a2增加到一定数值时,与y1或y2接近,使得式(15)的右侧分母项明显减小,进而大幅增加n.

图14 n与预应力筋位置的关系Fig.14 Relationship between n and prestressed tendonpositions

将预应力筋数量与各影响因素的关系总结为表3,表中同时给出了各影响因素与n的相关程度(用*的个数表示,最多5个*).

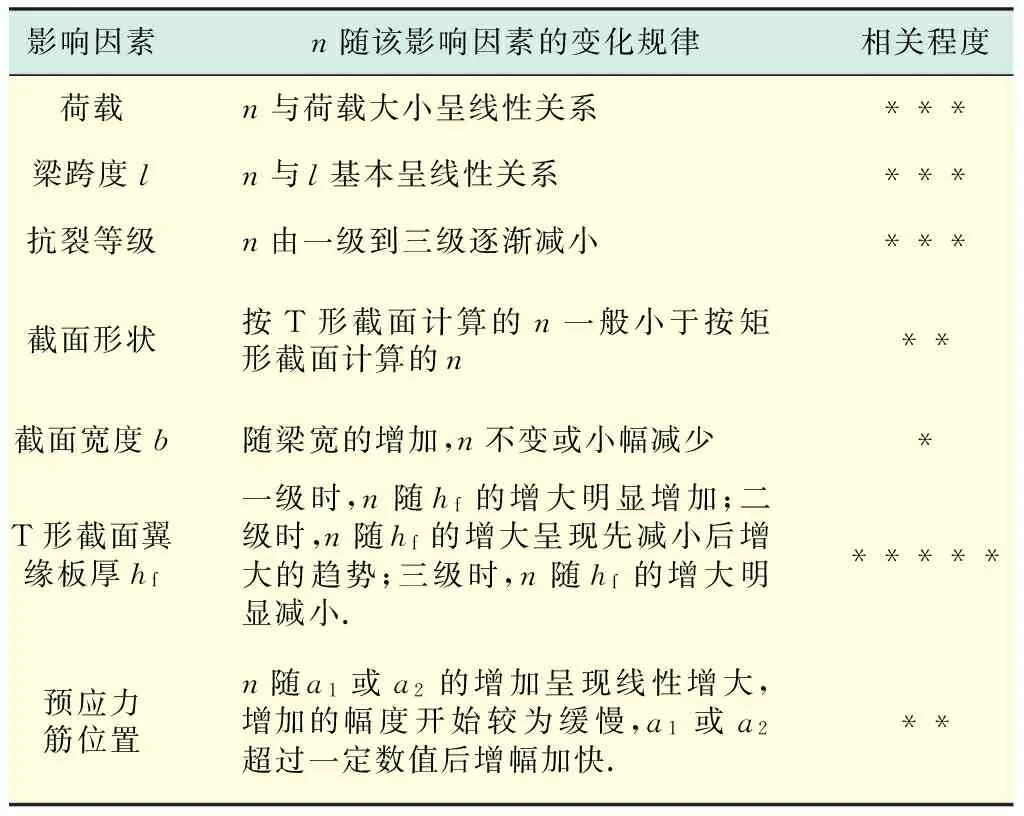
表3 n值与各影响因素的关系表Tab.3 Relations between n and various influential factors

4 结 论

a. 预应力梁按抗裂计算所需的预应力筋根数的影响因素较多,决不能单独根据跨度的大小直接预估.

b. 对预应力筋数量影响较大的因素有:荷载大小、梁跨度、抗裂等级、T形截面的翼缘板厚,其中,后者的影响效果最大.

c. 对预应力筋数量影响较小的因素有:梁的截面宽度、梁的截面形状、预应力筋在截面的位置.增加梁截面宽度或改变预应力筋在梁高度方向的位置并不能有效减少预应力筋的数量.

d. 增加板厚(即增加T形截面的翼缘板厚度),在三级抗裂等级的情况下可以显著减少预应力筋数量.

e. 在方案及初步设计阶段,采用本文给出的估算式(15)可以方便地预估预应力筋抗裂计算所需的预应力筋数量.

[1] 蒋庆,叶献国,章益民,等.高强钢筋高强混凝土预应力梁抗裂性能试验研究[J].建筑结构学报,2014,35(12):51-57.

[2] 林同炎,伯恩斯.预应力混凝土结构设计[M].路湛沁,译.北京:铁道出版社,1983.

[3] 住房和城乡建设部.GB 50010—2010 混凝土结构设计规范(2015版)[S].北京:中国建筑工业出版社,2011.

[4] 住房和城乡建设部.JGJ 92—2016 无粘结预应力混凝土结构技术规程[S].北京:中国建筑工业出版社,2016.

[5] 施明征.基于名义拉应力法的预应力混凝土结构的裂缝控制[J].工业建筑,2013,43(11):64-66,11.

[6] International Conference of Building Officials.Uniform building code[M].Whittier,CA:International Conference of Building Officials,1997.

(编辑:石 瑛)

Discussion on the Number of Prestressed Tendons in Building Floor Beams and Its Influential Factors Based on Crack Resistance Requirement

XU Jianshe

(SchoolofEnvironmentandArchitecture,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

In the design of prestressed beams in building structures,the prediction of the number of prestreesed tendons is necessary.The tendon number meeting the demands of crack resistance was studied.The formulas for calculating the number of prestressed tendons under three crack resistance grades were listed.By introducing reasonable assumptions,the simplified calculation formulas for determining the tendon number at the mid-span and support point were provided.The various influential factors of the tendon number,e.g.,the beam section shape,span of the beam,section width,crack resistance grade,slab thickness and position of prestressed tendons were discussed respectively.The relationship curves between the number and various influenctial factors were presented.The impact extent of various factors on the number was compared.A relatively accurate basis for estimating the number of prestressed tendons in the primary design phase was provided for structural designers.

prestressedbeam;numberofprestressedtendons;crackresistance

1007-6735(2017)04-0396-07

10.13255/j.cnki.jusst.2017.04.015

2017-02-10

徐建设(1972-),男,高级工程师.研究方向:结构设计计算.E-mail:buildxu@163.com

TU 378

A