双线浅埋隧道远近距离界定及地表沉降机理研究

，， ，

(河海大学 地球科学与工程学院，南京 211100)

双线浅埋隧道远近距离界定及地表沉降机理研究

王帅，孙少锐，舒杨，岳翎

(河海大学 地球科学与工程学院，南京 211100)

利用Peck公式计算双线隧道开挖引起的地表沉降时，有多个参数会影响到计算结果的大小与沉降曲线的形状。从数学角度对隧道轴线埋深h和两隧道间距L的比率及沉降槽宽度参数K对地表沉降曲线的影响进行研究，得到以下结论：在h/L比率逐渐增大的过程中，地表沉降曲线变化过程为较陡峭的W型—较平缓的W型—∪型—U型—V型；相同比率下的地表沉降曲线都呈现相同的型式，与隧道埋深无关；在K=0.600的情况下，沉降曲线由W型向U型转变，h/L的临界值为0.825，而后发现在不同K值下，存在h/L临界值使得不同埋深下的沉降曲线都呈现U型，得到了沉降槽宽度参数K与其对应h/L临界值的最优拟合方程。基于h/L临界值的分析结果，提出了双线隧道远近界线的判别公式，并与现有方法及规范进行对比，结果表明判别公式能较好地界定双线隧道远近距离。同时,对Peck公式预测隧道开挖引起地表沉降的机理进行了推测，并利用颗粒流软件对隧道开挖进行模拟，结果表明压力拱曲线符合高斯曲线。研究成果可为双线浅埋隧道设计、施工提供依据。

双线隧道；地表沉降；Peck公式；远近距离界线；颗粒流

1 研究背景

隧道的开挖施工必然会引起地表沉降，对周边建筑及管线产生不利影响。双线隧道因其跨度大、施工复杂，相比单洞，其对地层的扰动更大，所引起的地表沉降槽范围也随之增大。

近些年，通过对双线隧道开挖引起沉降问题的研究，国内外学者取得了一些成果：刘波等[1]研究了双孔平行隧道施工过程中地表纵向和横向沉降，并开发STEAD系统利用Peck公式和随机介质理论对沉降值进行计算;祝志恒等[2]对利用随机介质理论中的重要参数(主要影响角β及断面半径收敛值A)进行反分析，提高了地表位移计算的准确性。齐涛等[3]对Peck公式中的关键参数地层损失率提出优化方法，并对Peck公式进行了扩展;陈春来等[4]基于Peck公式，计算地表沉降过程中考虑先行隧道对后行隧道施工过程中的影响，并对Peck公式进行了修正;台启民等[5]对暗挖重叠隧道分别采用有限元法及Peck法进行了分析，并对公式中的相关参数进行了研究;D.E.Y. Elwood等[6]对连拱隧道中墙厚度对地表沉降的影响进行了分析;韩煊等[7]对随机介质理论及Peck法进行了深入分析，认为两者为相同的型式，而Peck法是随机介质理论的一个近似;而左昌群等[8]则基于分形理论，对隧道开挖引起地表沉降进行了分析及预测。由上可知，目前对于连拱隧道开挖引起地表沉降的主要研究方法有Peck公式法及修正Peck公式法、随机介质法、有限元分析法及现场监测法，应用最广泛的方法为Peck公式。但Peck公式法较多的还是用来进行拟合，而对其机理研究较少，需要更加深入的研究。

地表沉降是地下隧道开挖引起围岩或土体松动的宏观表现，研究隧道结构受力及应力分布，不可避免地要清楚隧道结构受力荷载及荷载分布型式，对于双线隧道来说，远近距离的判断是关键问题。至今，双线隧道远近距离临界值的计算尚无定论[9]。当上覆围岩厚度较小时，地表沉降对隧道开挖更加敏感。Peck公式的正确性及实用性已被广泛接受，在不能准确确定隧道开挖引起的压力拱上下界线或松动圈时，利用地表沉降的宏观表现对双线隧道的远近距离进行界定是可行的方法，能满足安全要求。另外，当两隧道距离过小时，会造成地表沉降较大，对周边环境产生较大影响。

本文基于Peck公式，针对隧道不同埋深h与不同间距L(两洞中心线间距离)之比、不同沉降槽宽度参数K值对双线浅埋隧道引起的地表沉降的影响进行分析；基于对Peck公式从数学角度分析的结果，推出了双线隧道远近距离的判断公式，结合工程实例，验证了公式的正确性；对Peck公式预测地表沉降机理进行推测，并用离散元软件进行模拟分析。研究结果可为后续工程的设计、施工提供参考。

2 地表沉降计算方法

R.B.Peck[10]在分析大量工程实践的基础上，提出隧道开挖引起的地表沉降曲线符合正态分布，并认为隧道在施工中地层损失的体积等于地表沉降槽的体积。地层损失是针对稳定的地下工程来说的，即忽略了围岩塑性变形和局部坍塌。而Peck公式也是基于稳定隧道工程统计得到的公式，所以能准确地预测地表沉降。如隧道围岩发生较小体积坍塌或局部产生塑性变形，Peck公式仍可应用于地表沉降预测。

单洞引起的地表沉降的计算公式为：

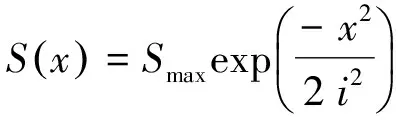
(1)

(2)

式中：Smax为洞轴线最大沉降值；x为地表某点到隧道中心线的水平距离；S(x)为其x对应处的沉降值；i为地表沉降槽宽度系数；Vl为开挖引起的地层损失率；A为开挖断面面积。

沉降槽宽度系数i为沉降槽曲线反弯点到隧道中心线之间的距离，先前学者对其进行了大量的研究。R.B.Peck[10]和N.Logamathan等[11]认为i和隧道的埋深h及断面半径R有关，而O’Reilly[12]和W.J.Ranki[13]基于监测数据提出的i与h之间呈线性关系这一观点应用最为广泛，其公式为

i=Kh。

(3)

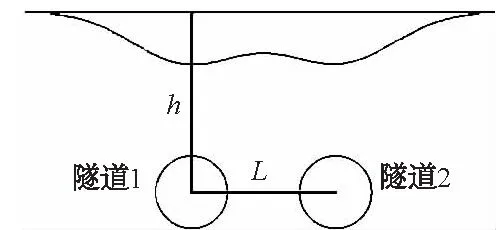
图1 双线隧道开挖示意图Fig.1 Sketch of double-track tunnel excavation

式中K为沉降槽宽度参数，主要与地质条件等因素有关。

由式(1)—式(3)可得到计算单洞横向地表沉降公式，即

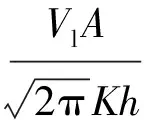
(4)

对于处于同一水平双线隧道(如图1)，隧道间距为L，假设隧道1(左侧)和隧道2(右侧)的地层损失率分别为Vl1和Vl2，沉降槽宽度参数为K1和K2，埋深分别为h1和h2，断面面积分别为A1和A2。则隧道1引起的地表沉降值为

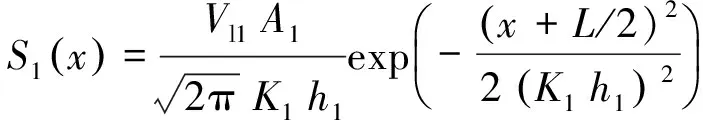
(5)

隧道2引起的地表沉降为

(6)

由叠加原理可知，隧道1、隧道2开挖所导致的地表沉降的计算公式为

(7)

而对于大多数隧道工程来说，两平行隧道的断面型式是相同的，并且隧道间距较小，岩土体性质相近，所以，岩土体底层损失体积可看作是相同的。对一般的市政工程隧道来讲，沉降槽宽度系数也是相同的，且隧道为圆形断面。当不考虑地形起伏、施工工序不同、断面型式为圆形时，视为均一介质中开挖的一般的双线地铁隧道，其地表沉降计算公式可简化为

(8)

3 计算参数对地表沉降的影响

利用Peck公式计算隧道开挖引起的地表沉降时，有多个参数会影响到计算结果的大小。另外，地表沉降曲线的形状也和参数的选取有关，所以，对Peck公式中参数选取对计算结果影响的研究是必要的。韩煊[14]、陈春来等[4]研究了埋深h及不同跨度对地表沉降的影响。本文对前人研究成果进行补充与拓展，通过研究参数对地表沉降的影响，为隧道设计施工提供参考。

在Peck公式中，决定最大位移位置的参数是L，与R和净距是无关的，所以，在分析沉降曲线的形状时，可不考虑断面形状及净距的影响。

3.1 h/L的变化

平行隧道开挖引起的地表沉降呈现为W型或V型，不仅和两隧道间距有关，也和隧道轴线的埋深有关。分析Peck公式可知，影响地表沉降曲线的参数为h,L,K。而K为沉降槽宽度参数，其取值和隧址区地质条件相关，为不可控因素。由前人研究可知，h减小及L的增大都会使得地表沉降曲线的型式由V型向W型过渡。本文对h/L值的变化对沉降曲线的影响进行分析。不考虑隧道施工工序及地质条件的影响，计算参数取Vl1=Vl2=1.221，K1=K2=0.596，隧道半径都为6 m，改变h及L，使得h/L分别取0.400，0.500，0.625，0.750，0.800,0.825，0.850，1.000，3.000时，对h/L的变化对曲线的影响进行了详细分析。

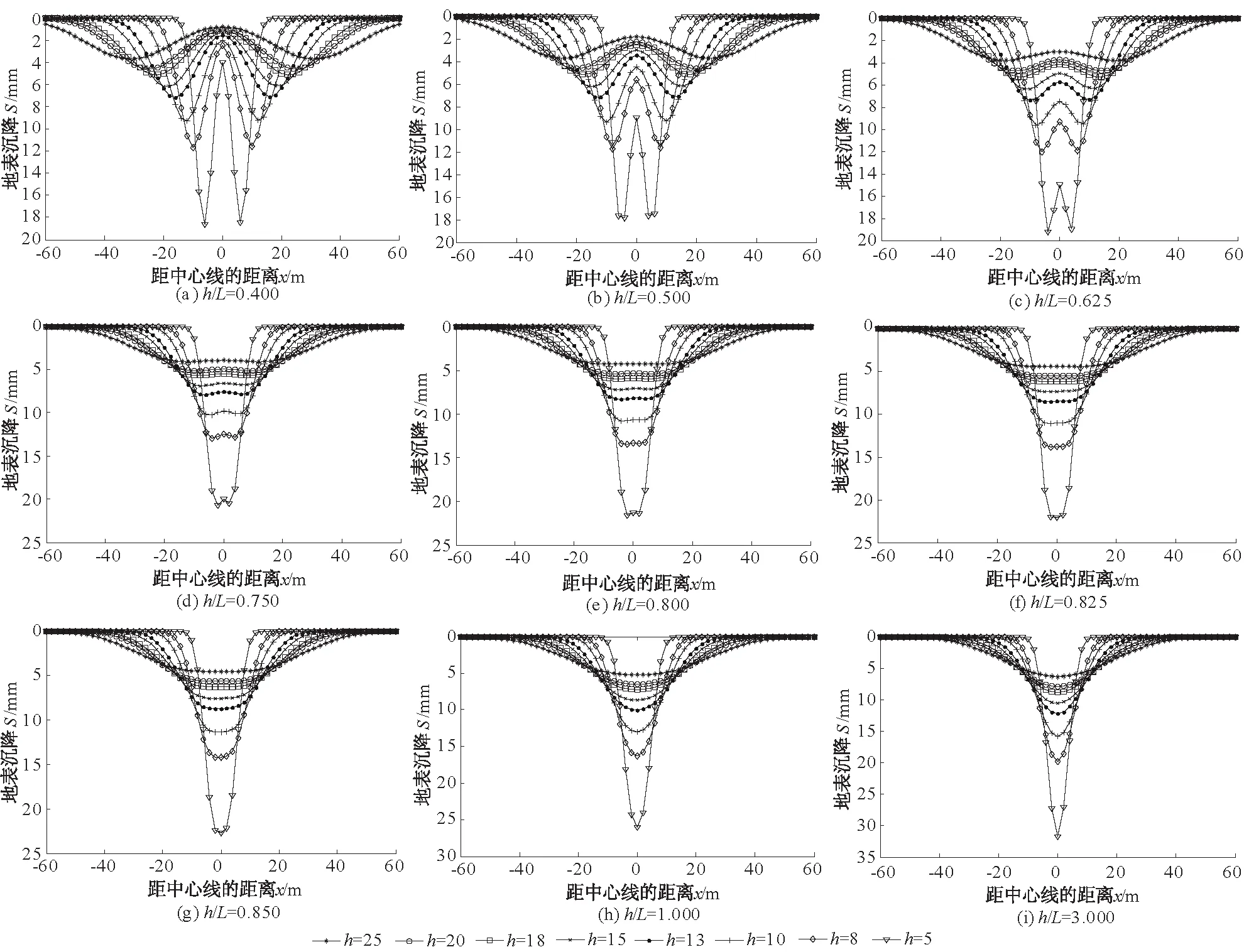
图2 不同h/L下隧道开挖引起的地表沉降曲线Fig.2 Curves of surface settlement caused by tunnel excavation with varying values of h/L

图2为不同h/L比率下双线隧道开挖引起的地表沉降曲线。从图2可以看出，在h/L比率逐渐增大的过程中，相同比率下的地表沉降曲线都呈现相同的型式，而与隧道埋深无关。地表沉降曲线变化过程为：较陡峭的W型—较平缓的W型—∪型—U型-较陡峭的V型。在K=0.600的情况下，沉降曲线由W型向V型转变,h/L的临界值为0.825。即在任何埋深情况下，双线隧道开挖引起的地表沉降曲线都呈现出∪型，此时h/L=0.825(图2(f))。另外，最大沉降随着h/L的增大逐渐增大，由16.2 mm增大到32.5 mm，增大1倍左右。图2(a)为h/L=0.400情况下的一系列地表沉降曲线，此种情况下，两平行隧道为远距隧道，双洞开挖引起的地表沉降曲线与单洞开挖引起的沉降曲线非常相似。

图2(i)为h/L=3.000条件下的地表沉降曲线，从该图中可以看出，随着埋深的减小，V型沉降曲线更加陡峭，这是因为高跨比大，隧道间距小，双线隧道开挖与单洞开挖引起的围岩扰动是近似的，所以沉降曲线完全呈现出断面稍大的单洞开挖引起的地表沉降曲线的型式。

3.2 K的影响

在3.1节中分析了当K=0.600情况下隧道开挖引起的地表沉降型式的变化，而在实际工程中，K值与隧址区的围岩条件相关，不同地质条件下，K的取值不同。R.J.Mair等[15]结合伦敦隧道工程实例，分析认为K值应取0.50;韩煊[14]对不同地区不同地质条件下的沉降槽宽度参数K值进行整理统计;王霆等[16]对不同开挖方法下的K值进行了分析;房倩等[17]对重叠隧道中双洞K的取值进行了研究;严健等[18]将Peck公式应用于藏区公路隧道施工引起地面沉降预测，拟合得出K值。本文对不同K值下是否存在h/L临界值使得地表沉降由W型转变为V型进行研究。通过MATLAB编制相应的计算程序，选出最佳的h/L临界值。图3中绘制了沉降槽宽度参数K与其对应的h/L临界值散点图，并对其进行拟合，最优拟合方程为

h/L=0.494 9K-0.975。

(9)

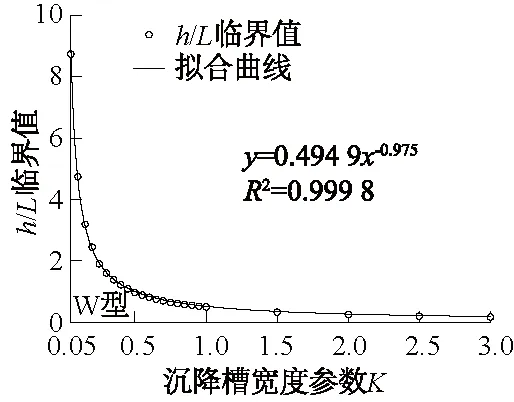
图3 h/L临界值与K的关系曲线Fig.3 Curve of critical value of h/L vs. K

R2=0.999 8，非常接近1，表明K与h/L临界值几乎完全符合拟合方程。从图3可看出，随着K值的增大，h/L临界值逐渐减小，当K=0.600时，h/L临界值为0.82，这与上文中K=0.596，h/L临界值取0.825的结果是相似的。

需要补充的是，当K>3时，仍存在h/L临界值使得沉降曲线为W到V型的过渡，且符合上述拟合方程。但由于此时的h/L临界值非常小且很接近，所以未绘出相关曲线。当已知沉降槽宽度参数时，可由该方程确定h/L的临界比率。将实际h/L比值与由式(9)计算所得的临界值进行比较，当实际值大于计算临界值时，地表沉降沉降曲线为V型，反之则为W型。

4 双线隧道远近距离界线的确定

4.1 双线隧道远近距离判定

由于地质条件的复杂，对于双线隧道远近距离的界定还无定论。魏纲等[9]用水平距离系数C=L/(h+R)来判断双线隧道的远近距离，认为C≤0.66时两隧道为近距离隧道;而陈春来等[4]则认为该值应为0.50。由水平距离系数计算公式可知，未考虑隧道围岩岩性的影响，不同条件下会得到不同的C值。而隧道的远近距离决定着隧道的受力型式，关乎到隧道施工方法及支护方案的设计，因此远近距离的判定这个问题亟待解决。

Peck公式预测单洞及双洞开挖引起的地表沉降是可行的，在上文从数学角度的分析中可知，不同K值下，都存在一个h/L的临界值使得双线隧道地表沉降从W型过渡到V型。结合压力拱理论中隧道围岩受力分析，可推知当地表沉降曲线为W型时，双线隧道为远距离隧道；当地表沉降曲线为V型时，隧道为近距离隧道。沉降槽宽度参数可由临近工程或类似地质条件下工程中获取，当K已知时，根据式(9)，即可求得h/L的临界值。当分析隧道开挖过程中围岩受力或位移时，若h已知，则可按照式(10)求得远近距离界线值，即

Lcr=2.021hK0.975。

(10)

当L≤Lcr时，双线隧道为近距离隧道，地表沉降曲线为V型；当L>Lcr时，双线隧道为远距离隧道，地表沉降曲线呈现为W型。

在Peck公式和本文提出的远近距离界线判别公式中，沉降槽宽度参数K都是极其重要的参数。由式(10)可知，隧道围岩性质越好时，K值越小。此结论和Peck[9]和Knothe[10]对K值的研究成果不相同，即岩土体力学性质越好，其K值越大，而与韩煊[14]的研究成果一致。分析可知，任何K值下，都存在相对应唯一的h/L值，使得地表沉降曲线呈∪型。对于K值的研究尚无定论，因篇幅有限，此处对K的取值不做过多分析。

4.2 与现有判别方法对比及算例分析

现有的远近距离判别公式较少，现行《公路隧道设计规范》(JTG D70—2004)[20]对不同围岩类别下双线隧道的最小净距进行了规定，但通过统计国内双线隧道工程实例可知，规范规定值大多情况下偏大。胡元芳[21]基于双线隧道中间岩柱不破坏、隧道围岩破坏区不相交的原则，在双线隧道净距优化上取得较大突破，其提出的最小净距参考值(范围)小于规范值。将本文提出的方法与现行规范及胡元芳提出的最小间距对比，结果见图4。

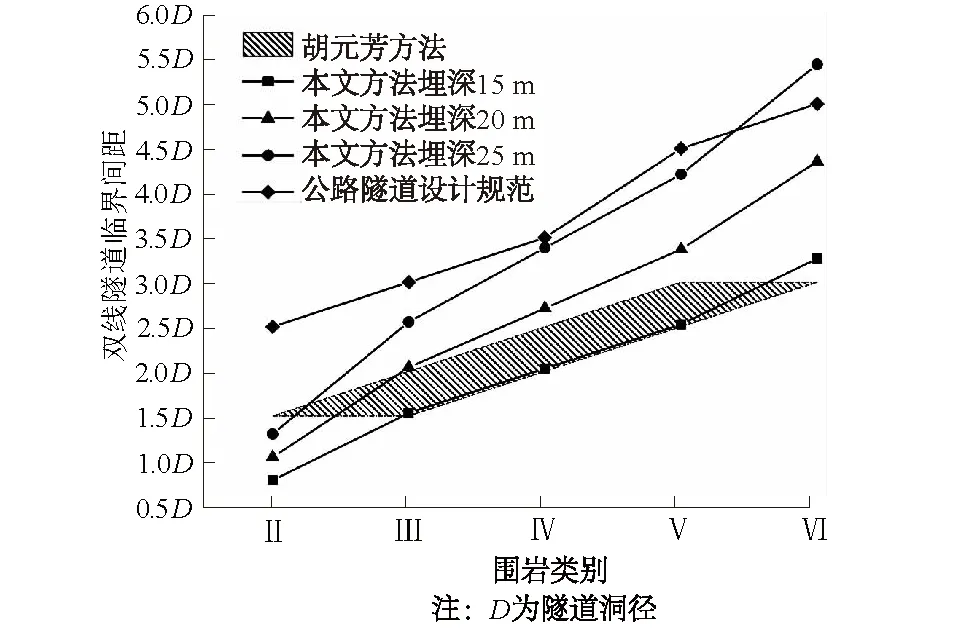
图4 本文方法与现有方法对比Fig.4 Comparison between the proposed method and the existing methods

由图4可知，隧道轴线埋深为15～20 m时，不同围岩类别下本文方法计算两洞临界间距基本符合胡元芳提出的参考值，但明显小于规范参考值。当隧道轴线埋深为25 m时，除Ⅱ类围岩外，其他围岩类别下本文方法计算临界间距与规范参考值相一致。分析可得，胡元芳研究的是浅埋双线城市隧道，所以当隧道埋深浅时，本文方法计算结果与其相符。而规范中的最小净距是通过圆孔弹性力学计算所得，其结果更符合埋深较深条件。浅埋条件下，其参考值偏大。本文方法考虑了地质条件的影响，其结果与现有规范及先前学者的优化结果相符，证明了公式的正确性。另外，本文公式考虑了隧道埋深的影响，使其更具有普遍性，且更加精确。

根据部分学者对双线隧道开挖引起地表沉降的监测成果及实测数据，对4.1节提出的双线隧道远近距离判别公式进行验证，结果见表1。

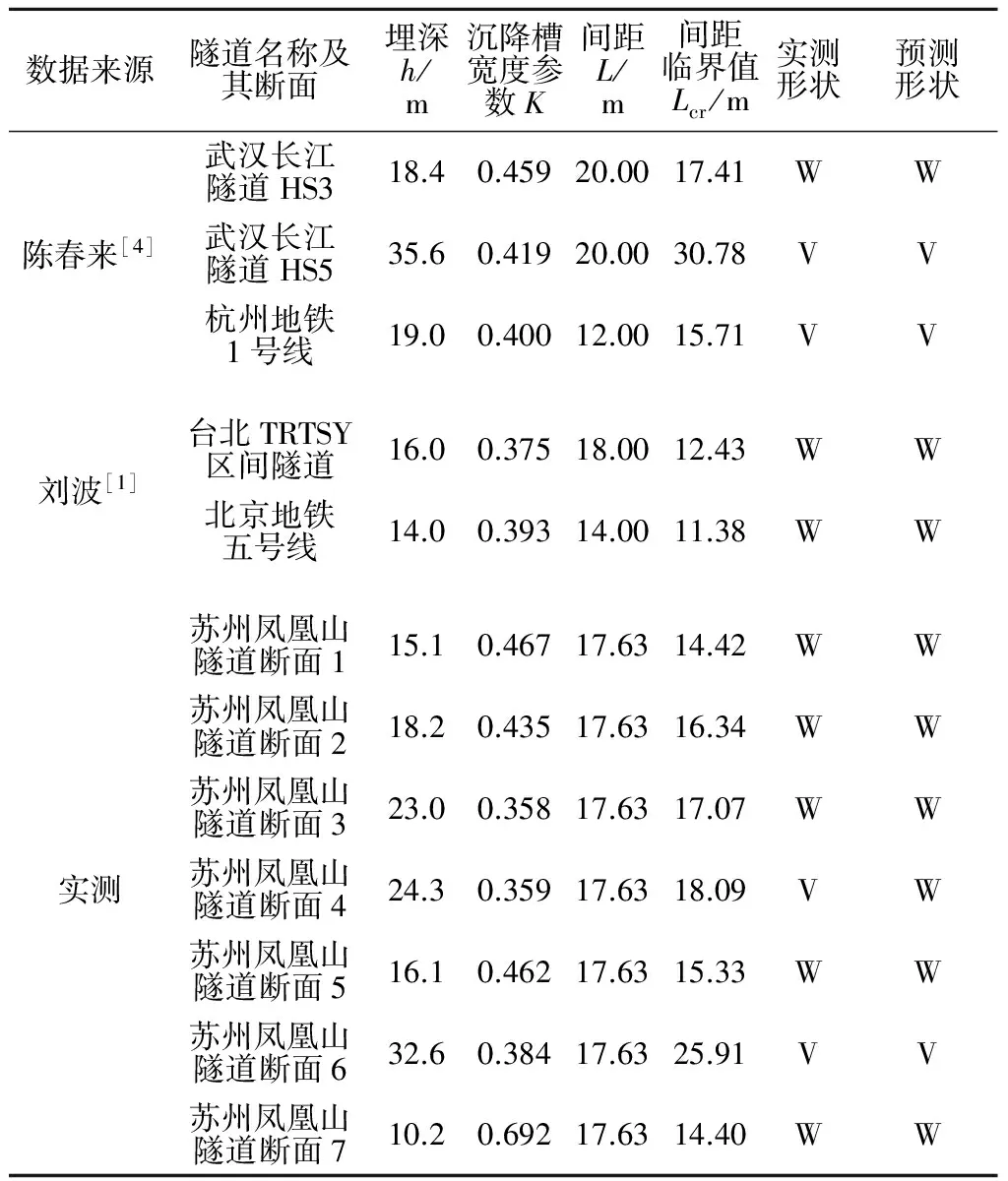
表1 双线隧道地表沉降曲线实测型式与预测型式对比

从表1中可看出，除苏州凤凰山隧道断面4外，其他所有隧道断面开挖引起的地表沉降曲线的实测形状与预测形状相符。而凤凰山隧道断面4的临界值与实际间距相差很小，为0.46 m，可能因施工影响而造成监测结果与预测结果不符。

综上所述，本文提出的远近距离判别公式能较好地判别隧道远近距离。

5 Peck公式预测地表沉降的机理

经众多学者验证，Peck公式能够较准确地预测隧道开挖引起的地表沉降，但其预测沉降的内在机理尚不清楚。由以上分析可推测，对于单洞来说，隧道开挖引起地表沉降，其沉降曲线满足高斯曲线，这是单洞开挖后形成稳定压力拱的宏观表现。对于远距离双线隧道，可认为是两单洞开挖，不能形成一个整体的稳定的压力拱;而对于近距离双线隧道来说，隧道开挖后在各单洞形成稳定压力拱的条件下，由于相互影响而形成一个面积更大的压力拱时，地表沉降曲线呈现出W型或V型。

当沉降曲线呈W型时，表明双线隧道形成完整的压力拱，但中间岩柱依然承受上部岩体压力，使得两隧道中线处地表沉降减小。而当隧道距离适当近时，双线隧道开挖可在其上方形成稳定的压力拱，中间岩柱由于受力过大而发生破坏，无支护能力，则在中心线处的地表沉降值最大，这与V型地表沉降曲线相一致。简而言之，即压力拱顶部的形态决定着沉降曲线的形态，沉降槽宽度系数则与压力拱的左右边界有关，可在下一步工作中对压力拱的形状与地表沉降曲线之间的关系进行研究。

为验证以上推测，利用离散元软件PFC进行数值模拟。数值模型尺寸为50 m×40 m，颗粒半径为8～12 cm均匀分布，颗粒间的微观参数采用朱伟等[22]标定的参数，颗粒密度为2 630 kg/m3，摩擦系数为1.9，颗粒法向刚度与切向刚度都为1.4×108N/m，墙的法向刚度与切向刚度都取2×108N/m。为模拟自然状态下隧道开挖产生的压力拱，颗粒生成时模型达到重力平衡。隧道开挖后不设置圆形墙体，数值模型重新达到平衡。

利用颗粒流数值模型分析了不同埋深、不同半径单双洞隧道开挖后压力拱形态，因篇幅有限，仅对4种情况进行分析(见表2)。图5为颗粒速度矢量分布图，黑色箭头代表速度矢量，由速度矢量图可看出围岩破坏情况。

表2 分析案例及其结果Table 2 Case analysis and the results

图5 隧道开挖后颗粒接触力及速度矢量分布Fig.5 Distribution of velocity vector after excavation

由于隧道的开挖，隧道周边颗粒发生移动，隧道顶部颗粒发生塌落。在速度矢量图中，压力拱的存在及位置比较明显。在图中可清晰看到距洞顶一定距离处，颗粒速度很小或者为0，处于稳定状态。而处于这一状态的颗粒呈一定厚度的条带状，即为压力拱，这与郑康成等[23]的研究成果相同。隧道开挖后产生的压力拱上下界线如图5中白线所示。对于单洞隧道，隧道开挖后形成一个稳定的压力拱，半径较小的单洞隧道形成的压力拱厚度较小；对于双洞隧道，当两隧道间距较大时，压力拱呈现为反W型。而当两隧道间距较小时，双洞洞顶形成的压力拱型式与单洞相似。这和利用Peck公式预测的远距离双线隧道沉降结果相对应。

以数值模型底板中点为圆心，水平方向向右、竖直方向向上分别为x轴正方向、y轴正方向建立坐标系。对压力拱下边界曲线分别进行高斯拟合，拟合结果见表3。由表3可知，埋深相同时，半径为3 m和半径为6 m的单洞隧道压力拱曲线相近，高斯拟合参数相近，这与Peck公式中半径变化对沉降曲线型式无影响一致。另外，单双洞状态下，高斯拟合效果都很好，R2>0.95，和方差与均方根误差都很小。

表3 压力拱曲线拟合结果Table 3 Fitting results of pressure-arch curve

综上所述，隧道开挖产生的压力拱曲线满足高斯函数，印证了上文的推测，即压力拱的型式决定了地表的沉降，而Peck公式能较好地预测隧道开挖引起的地表沉降也是基于此。

6 结 论

基于广泛采用的预测双线浅埋隧道开挖引起地表沉降的Peck公式，从数学角度对其进行分析各参数对公式结算结果的影响，并对其预测地表沉降的机理进行研究，得到如下结论。

(1) 在h/L比率逐渐增大的过程中，相同比率下的地表沉降曲线都呈现相同的型式，而与隧道埋深无关。地表沉降曲线变化过程为：较陡峭的W型—较平缓的W型—∪型—U型—较陡峭的V型。在K=0.600的情况下，沉降曲线由W型向U型转变的h/L临界值为0.825。

(2) 对不同K值下是否存在h/L临界值进行研究，绘制了沉降槽宽度参数K与其对应h/L临界值散点图，得到最优拟合方程。当已知沉降槽宽度参数K时，可由该方程确定h/L的临界比率。当实际值大于计算临界值时，地表沉降曲线为V型，反之则为W型。

(3) 基于h/L临界值的分析结果，提出了双线浅埋隧道远近距离判别公式，即Lcr=2.021hK0.975，并采用前人文献数据验证了推测的正确性与适用性。

(4) 对Peck公式预测隧道地表沉降的机理进行推测分析，认为压力拱顶部的形态决定着沉降曲线的形态。利用颗粒流程序(PFC)对隧道开挖后产生的压力拱进行模拟分析，高斯函数能很好地拟合单洞隧道及双线隧道压力拱曲线，验证了推测的正确性。下一步应进行模型试验，对此结论进行验证。

[1] 刘 波, 陶龙光, 叶圣国, 等. 地铁隧道施工引起地层变形的反分析预测系统[J]. 中国矿业大学学报, 2004, 33(3): 277-282.

[2] 祝志恒, 阳军生, 董 辉. 双洞隧道施工引起地表移动的多参数反分析研究[J]. 岩土力学, 2010, 31(1): 293-298.

[3] 齐 涛, 张庆贺, 胡向东, 等. 一种盾构掘进引起地表沉降的实用预测方法[J]. 岩土力学, 2010, 31(4): 1247-1252.

[4] 陈春来, 赵城丽, 魏 纲, 等. 基于 Peck 公式的双线盾构引起的土体沉降预测[J]. 岩土力学, 2014, 35(8): 2212-2218.

[5] 台启民, 张顶立, 房 倩, 等. 暗挖重叠地铁隧道地表变形特性分析[J]. 岩石力学与工程学报, 2014, 33(12): 2472-2480.

[6] ELWOOD D E Y, MARTIN C D. Ground Response of Closely Spaced Twin Tunnels Constructed in Heavily Overconsolidated Soils[J]. Tunnelling and Underground Space Technology, 2016, 51: 226-237.

[7] 韩 煊, 李 宁. 隧道施工引起地层位移预测模型的对比分析[J]. 岩石力学与工程学报, 2007, 26(3): 594-600.

[8] 左昌群, 刘代国, 丁少林, 等. 基于分形理论的隧道地表沉降分析及预测[J]. 长江科学院院报, 2016, 33(4): 51-56.

[9] 魏 纲, 庞思远. 基于有限元模拟的双线平行盾构隧道近距离界定[J]. 市政技术, 2014, 32(1): 76-80.[10]PECK R B.Deep Excavations and Tunneling in Soft Ground[C]∥Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City, 1969: 225-290.[11]LOGANATHAN N, POULOS H G. Analytical Prediction for Tunneling-induced Ground Movements in Clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124 (9): 846-856.

[12]O’REILLY M P，NEW B M. Settlements above Tunnels in the United Kingdom:Their Magnitude and Prediction[C]∥Proceedings of Tunnelling 82. London：Institution of Mining and Metallurgy. June 7-11, 1982: 173-181.

[13]RANKIN W J. Ground Movement Resulting from Urban Tunnelling: Predictions and Effects[C]∥ Nottingham University. Proceedings of the 23rd Annual Conference of the Engineering Group of the Geological Society. London: Engineering Geology Special Publications. September 13-17, 1987: 79-92.

[14]韩 煊. 隧道施工引起的地层位移及建筑物变形预测的实用方法研究 [D]. 西安: 西安理工大学, 2006.

[15]MAIR R J, TAYLOR R N, BRACEGIRDLE A. Subsurface Settlement Profiles above Tunnels in Clays[J]. Geotechnique, 1993, 43(2): 315-320.

[16]王 霆, 刘维宁, 张成满, 等. 地铁车站浅埋暗挖法施工引起地表沉降规律研究[J]. 岩石力学与工程学报, 2007, 26(9): 1855-1861.

[17]FANG Q, TAI Q, ZHANG D,etal. Ground Surface Settlements due to Construction of Closely-spaced Twin Tunnels with Different Geometric Arrangements[J]. Tunnelling and Underground Space Technology, 2016, 51: 144-151.

[18]严 健, 何 川, 吴海彬, 等. 基于 Peck 公式的藏区公路隧道施工地面沉降预测[J]. 公路交通科技, 2015, 32(1): 110-115.[19]KNOTHE S. Observations of Surface Movements under Influence of Mining and Their Theoretical Interpretation[C]∥Proceedings of European Conference on Ground Movement. Leeds, UK: University of Leeds, 1957: 210-218.[20]JTG D70—2004, 公路隧道设计规范[S].北京:人民交通出版社，2004.

[21]胡元芳. 小线间距城市双线隧道围岩稳定性分析[J]. 岩石力学与工程学报, 2002, 21(9): 1335-1338.

[22]朱 伟, 钟小春, 加 瑞. 盾构隧道垂直土压力松动效应的颗粒流模拟[J]. 岩土工程学报, 2008, 30(5): 750-754.

[23]郑康成, 丁文其, 金 威. 基于模型试验与FEM的TBM圆形隧道压力拱成拱规律[J]. 煤炭学报, 2015, 40(6): 1269-1274.

(编辑：陈 敏)

Critical Distance of Shallow Twin Tunnels and GroundSurface Settlements Caused by Tunneling

WANG Shuai, SUN Shao-rui, SHU Yang, YUE Ling
(School of Earth Sciences and Engineering, Hohai University, Nanjing 211100, China)

When Peck’s formula is used to calculate surface settlements caused by tunneling, the calculation results and the shape of settlement curves are affected by multiple parameters. In the present research, the effects of the ratio of depth of tunnel axis (h) to chamber distance (L) and the settlement tough width parameterKon the ground surface settlement curve were analyzed in a mathematical sense. Results revealed that as the value of ratio ofh/Lincreases, the shape of surface settlement curve transformed from steep dual peak (W) to flat dual peak, and then to U-shape and V-shape successively. The shape of the curves remained the same under the sameh/Lratio, but had nothing to do with the value ofh. In the case ofK= 0.600, when the value ofh/Lwas equal to 0.825, the settlement curves changed from W-shape to U-shape exactly. Moreover, in the presence of differentKvalues, a unique critical value ofh/Lexisted when the shape of settlement curves achieved critical U-shape. The fitting curve was obtained to express the relation between the critical value ofh/LandK. Furthermore, the formula for the critical distance of twin tunnels is proposed based on the relation between the critical value ofh/LandKby comparing the formula with other methods and current specification, and the result indicates that the proposed formula is reasonable and accurate. According to the above results, the mechanism of predicting excavation-induced surface subsidence by Peck’s formula is presented. Simulation on the excavation by particle flow code indicated that the pressure-arch corresponded to Gaussian curve. The research provides reference for the design and construction of shallow twin tunnels.

twin tunnels; surface settlement; Peck’s formula; critical distance; particle flow code

2016-05-18；

：2016-07-01

国家自然科学基金项目(41002089，41102162)

王 帅(1991-)，男，河南许昌人，硕士研究生，主要从事岩体结构稳定性方面的研究工作,(电话)18251828317(电子信箱)youngrunner_w@163.com。

10.11988/ckyyb.20160521

2017,34(9):115-121

U451

：A

：1001-5485(2017)09-0115-07