梯级水库溃坝洪水对下游城市的淹没过程分析

，,2，

( 1.三峡大学 水利与环境学院，湖北 宜昌 443002；2.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌 443002)

梯级水库溃坝洪水对下游城市的淹没过程分析

杨忠勇1，郭红民1,2，曹光春1

( 1.三峡大学 水利与环境学院，湖北 宜昌 443002；2.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌 443002)

溃坝洪水的演进过程及其对下游城市的淹没影响是大坝安全的重要研究内容之一。以我国南方某山区河流为例，采用数值计算方法，针对该流域上并(串)联的4座水库在多种溃坝模式下，对下游城市的淹没过程进行了计算和讨论分析。研究结果表明：溃坝洪水在下游城市的淹没速度和最大淹没面积主要与最大溃坝流量相关，即与溃坝水头和溃口大小相关；最大淹没面积的达到时间主要与城市与水库间的行洪距离有关。梯级水库发生连溃时，溃坝洪水对下游城市的淹没速度和淹没面积都较单个水库溃坝更加严重，不过连溃洪水在下游城市呈现淹没快、退水也快的特征。城市洪水的淹没历时主要与溃坝水库的容积相关，与最大溃坝流量的关系不大。

梯级水库；溃坝洪水；淹没面积；溃坝流量；淹没历时

1 研究背景

水库和大坝安全是水工建筑物设计和维护的核心问题，虽然每个坝体的设计和运行都是依规范而行，但溃坝还是时有发生，如1975年河南省板桥、石漫滩两座坝体的溃决[1]，2010年美国德里湖大坝溃决等[2]。大坝溃决后，溃坝洪水将给下游城市居民带来灾难性的后果，因此有必要对溃坝洪水的传播特征以及对下游城市的淹没范围等展开专门研究，一来可对溃坝洪水的演进过程做出预报，二来还可对下游城市不同区域的危险等级进行评估。

溃坝洪水由于事发突然，历史上对它的实测资料研究较少，目前对其研究通常是采用数值计算或物理模型试验来实现的。1871年圣·维南方程组的提出为溃坝洪水的模拟计算提供了理论基础。在此基础上，里特(Ritter)[3]于1892年推导出了在忽略底摩擦情况下矩形渠道中的瞬时全溃流量公式；斯托克(Stoker)[4]将坝体溃决过程分为3种流态分别讨论，包括连续波流、临界流和不连续流。1980年林秉南等[5]针对平底无阻力有限长度库区的情况,通过特征线法、映像函数法和勒让德函数法等推导出了溃坝流量过程的近似解；谢任之[6]针对多种河谷断面，从逐渐溃、部分溃、瞬时全溃等多个角度分别提出了最大溃坝流量及水库泄空时间等参数的理论和经验计算公式；2007年符传君等[7]采用有限体积法建立了溃坝洪水演进过程数学模型，主要讨论了弯曲河道和障碍物对洪水波传播的影响；2010年曹志先等[8]结合数值模拟与物理模型试验，对溃坝洪水的流速分布特征进行了研究，并分析了洪水中泥沙输运和坝体侵蚀的主要影响因素。在梯级水库溃坝方面也有部分研究成果[9-11]，但主要在于讨论溃坝流量过程，或是下游洪水的演进特征，而在溃坝洪水对下游城市的淹没影响方面还有待进一步探讨研究。

本文以我国南方某山区的S河流域为例，采用数值计算方法，对该流域上并(串)联的4座水库在不同溃坝组合条件下，其溃坝洪水波对下游不同距离的2座城市的淹没特征进行了讨论分析。研究结果可为该流域水库安全调度运行、下游城市规划、洪水预警及溃坝应对措施制定等提供参考依据，具有重要的理论及实践意义。

2 研究区域概况

S河流域各水库及城市相对位置见图1(a)所示。S河上游分为东、西2条支流，分别为ES河和WS河。WS河上游建有1座X水库，该水库大坝高87.5 m，总库容26.32亿m3；ES河上游建有1座F水库，该水库大坝高76 m，总库容4.91亿m3。ES河在F水库上游又分为2条支流，分别建有2座水库——M水库和B水库，M水库大坝高82 m，总库容3.37亿m3；B水库大坝高104 m，总库容4.60亿m3；M水库和B水库与F水库的坝址距离均约为25 km。整个流域主要分布有2座城市，其中L市位于ES河和WS河2支流汇合区域下游约17 km处，距上游X水库约58 km，距上游F水库约66 km；H市距上游的F水库约17 km。L市区内相对于附近河段水面的平均相对高程约20 m，且部分区域相对高程不足10 m(图1(b))，上游任何一个水库溃决都有可能对其造成淹没。H城市内大部分区域相对附近河段水面高程不足15 m(图1(c))。若F水库及上游的M和B两座水库坝体溃决，显然会对H市产生严重影响，另一方面，虽然X水库位于H市下游，其溃坝后产生的巨大流量仍然可能通过WS和ES的交汇口倒灌进入WS河上游，造成H市的淹没。

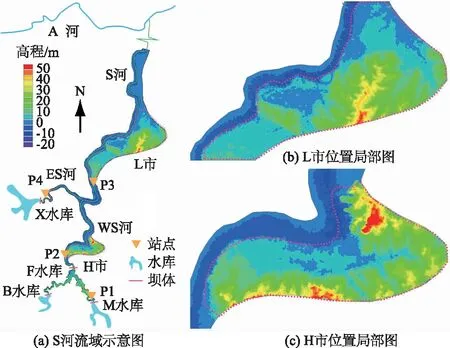
图1 研究区域概况及测点分布Fig.1 Overview of the study area and the distribution of observation sites

3 数学模型构建

3.1 模型范围及主要边界条件

为对S河上4个水库溃决后对下游城市的淹没范围进行模拟计算，本研究中采用平面二维水动力学数学模型MIKE21FM，模型中的无结构三角形网格可更好地拟合地形。模型范围见图1(a)所示，考虑溃坝洪水可能对河道周围产生淹没，因此模型范围大于原河道范围，特别是在H市和L市及其附近区域，所有可能被淹没的区域尽可能被包含在计算范围之中。模型中网格分辨率在40～100 m之间，三角形网格最小允许角度41°，相邻三角形面积比最小允许值为0.7。模型中河道水深数据来自实测资料，陆上地形高程来自美国航天飞机雷达地形测绘数据[12-13]，并由当地河道水面高程进行了矫正处理。水位初始条件给定为当地水面高程，流场初始条件为0。模型下游边界至L市下游约40 km处，边界条件给定为自由出流。上游边界至3个水库的坝体位置，边界条件采用流量给定。坝体未溃决时，流量数据采用枢纽运行规划要求流量，若坝体溃决，流量过程采用谢任之公式计算所得[14]。其中溃坝最大流量(Qm) 计算公式为

(1)

式中：λ=0.172,为经验流量参数；B为坝体宽度；H0为坝前水头；g为重力加速度。水库水体泄空时间te计算公式为

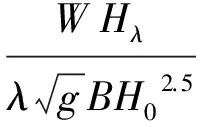
(2)

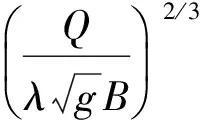
溃坝流量过程Qt可由最大溃坝流量Qm和水库泄空时间te求出，即Qt=tiQm/te，其中：ti≤te,为经验参数；D1，D2，ti的取值可参阅文献[14]。

3.2 工况设置

为研究不同溃坝组合条件下，溃坝洪水对下游城市的影响，本文共计算了10种工况,如表1。

表1 工况模式介绍及主要边界条件信息Table 1 Introduction of modeling situations and mainboundary conditions

3.3 模型验证

由于所研究的4个坝体从未发生溃决，因此模型的验证采用水库正常运行时段的水位特征进行。验证时段为某年7—8月份，验证结果如图2所示，计算值与实测值基本吻合，满足进一步研究的需要。

图2 各站点的水位验证Fig.2 Comparison of water level between modeled results and observed values

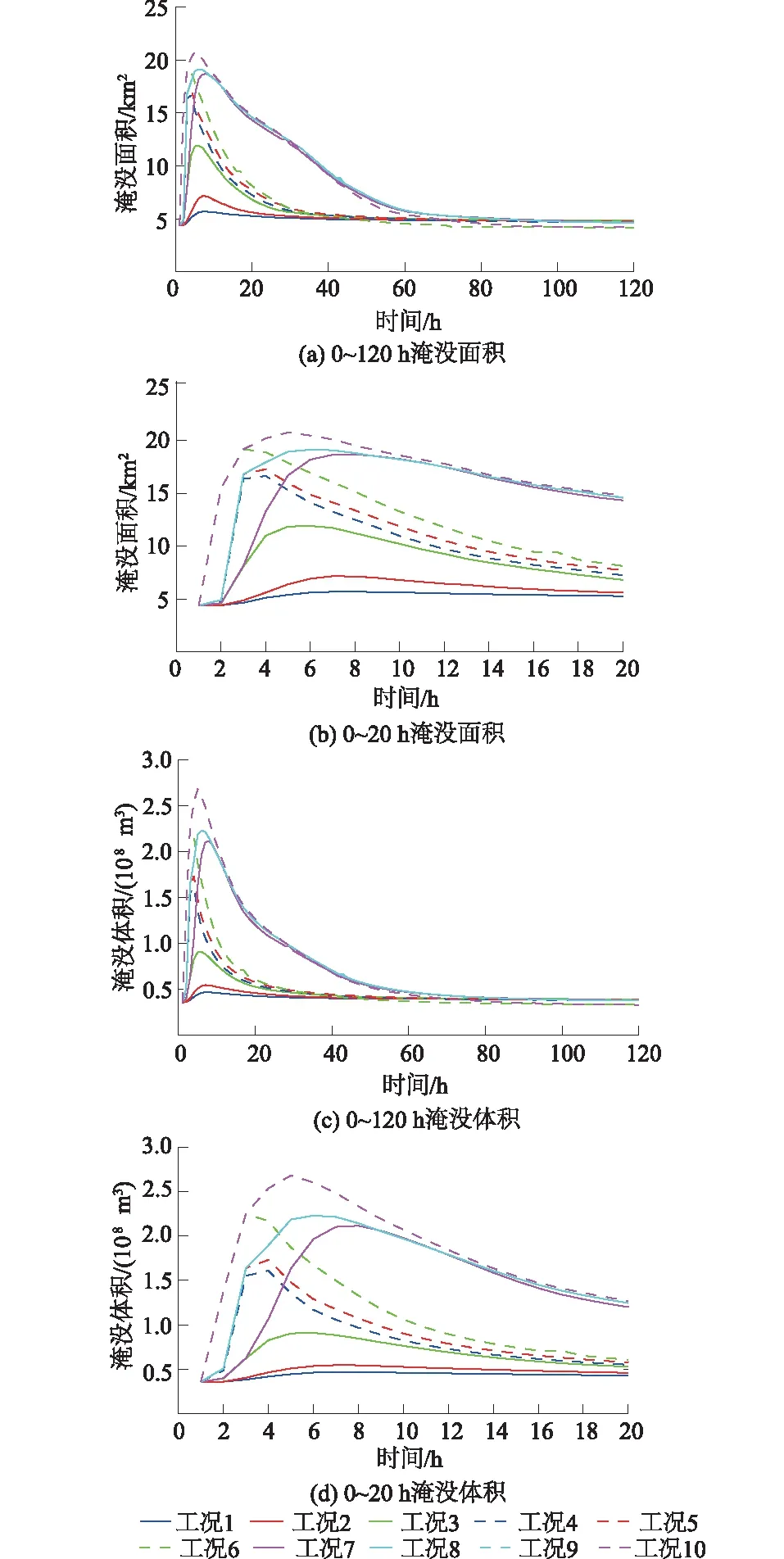
图3 不同工况下H市洪水面积及体积淹没过程Fig.3 Process lines of inundated area and volume in H city

4 溃坝洪水对下游城市的淹没过程分析

4.1 H市淹没过程分析

图3中显示了H市在各种工况模式下的淹没面积和淹没水体随时间的变化过程。若F水库坝体不溃，在M水库或B水库坝体单溃、F水库漫顶的情况下，H市的淹没程度是最小的。M水库单溃情况下(工况1)，H市的最大淹没面积约5.7 km2，最大淹没水体约0.47亿m3。B水库单溃情况下(工况2)，H市的最大淹没面积约7.2 km2，最大淹没水体约0.55亿m3。由于B水库的库容和大坝高度都略大于M水库，因此B水库的最大溃坝流量和溃坝后水库泄空时长都较M水库大，导致其溃坝洪水对H市的淹没面积和体积略大于M水库。若M水库和B水库同时发生溃决，F水库漫顶情况下(工况3)，H市的最大淹没面积和体积分别达到12 km2和0.91亿m3。在淹没历时上，工况1—工况3分别约在溃坝后6.8，6.7，5.9 h达到最大淹没面积，而后淹没面积逐渐减小，约43 h后，3种工况的淹没面积达最小，并基本保持恒定。需要说明的是，由于淹没面积和体积的统计范围内包括了部分S河河道和一些未统计的小支流内槽蓄的水体，因此淹没面积和体积始终>0。为此可以认为淹没面积达到最小值且保持恒定时即是淹没后退水完成时期。

若F水库坝体受上游溃坝洪水的影响，在水位达到坝顶时发生溃决，即产生水库连溃情况，其对下游H市的影响将显著扩大。由于F水库坝体对M水库和B水库的溃坝流量过程有一定缓冲作用，因此M水库与F水库连溃模式(工况4)和B水库与F水库连溃模式(工况5)对H市淹没面积的影响在达到最大淹没面积之前相差很小。这2种情况下，最大淹没面积和体积分别约17 km2和1.65亿m3，达到最大淹没面积的时长约3.5 h。达到最大淹没面积之后，由于B水库体积明显大于M水库体积，工况5的水库泄空时间大于工况4，因此H市淹没面积的下降过程中，工况5的淹没面积一直大于工况4，直至约45 h后淹没面积趋于恒定。若M水库和B水库同时溃决，F水库坝体也在溃坝洪水达到坝顶水位时溃决，最大淹没面积和体积分别可达19.2 km2和2.25亿m3，达到最大淹没面积的时长缩短为3.0 h。有趣的是，溃坝后约45 h后，H市淹没面积与前面几种工况一致，而随着时间的延长，淹没面积还进一步发生了略微的降低，主要原因在于上游所有坝体发生溃决过后，上游已无水库存在，因此来流量逐渐降低。

进一步考虑X水库对下游城市的影响，该水库位于H市下游，其对H市的影响要通过X水库溃坝洪水在WS河和ES河的交汇处往上游回流产生。因此若不考虑F水库的溃坝影响(工况7)，H市的淹没过程比较缓慢，溃坝约8.0 h后才达到最大淹没面积。然而，由于X水库体积非常大，达26亿m3，导致H市的最大淹没面积也比较大，达18.6 km2，最大淹没水体达2.1亿m3，水库泄空的时间也非常长，直到溃坝约69 h后淹没面积才趋于恒定。在X水库溃决的基础上，若考虑H市上游M水库和F水库的连溃(工况8)或是B水库和F水库的连溃(工况9)情况，则不管是淹没速度还是淹没面积都会进一步扩大。在这2种工况下，H市的淹没程度相差不大，最大淹没面积约发生在溃坝6.1 h后，最大淹没面积约19.1 km2，最大淹没水体约2.3亿m3。

若M水库和X水库同时溃决，并诱发F水库大坝溃决的同时，还叠加X水库的水库溃决洪水，将对H市产生最不利的淹没影响。这种情况下，H市的最大淹没面积约为20.8 km2，最大淹没水体约为2.7亿m3，大于其他所有情况。但最大淹没面积的达到时间约为4.5 h，大于工况4—工况6，其主要原因在于:当F水库、M水库和B水库3个水库的溃坝洪水对H市淹没后，X水库的洪水才逐渐到达。

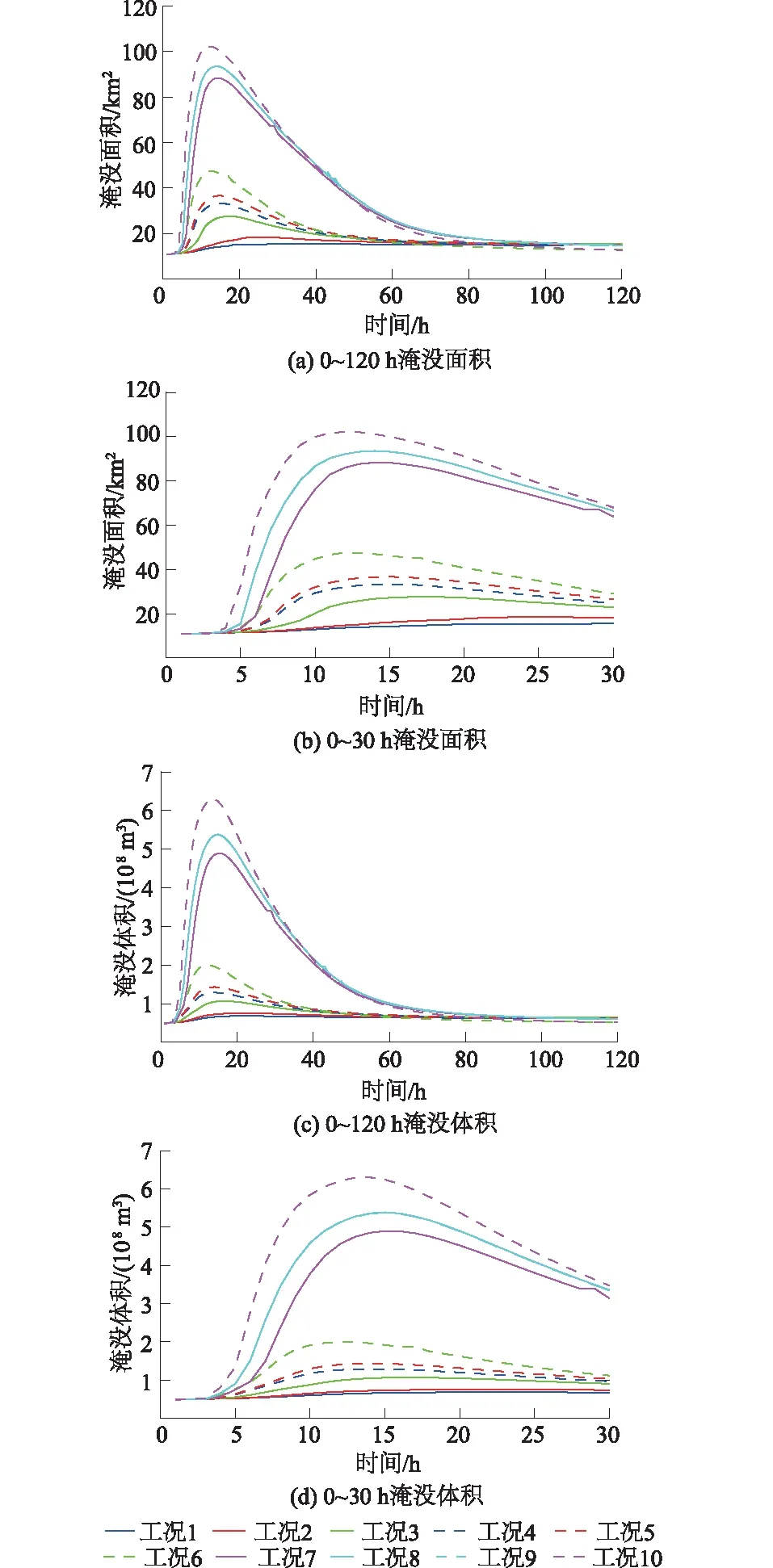
图4 不同工况下L市洪水面积及体积淹没过程Fig.4 Process lines of inundated area and volume in L city

4.2 L市淹没过程分析

图4中显示了L市在各种工况下的淹没面积和淹没水体随时间的变化过程。在M水库(工况1)或B水库(工况2)单溃，F水库漫顶不溃的情况下，L市的淹没速度非常缓慢，溃坝约30 h后淹没面积和体积达最大值，分别约15 km2和0.7亿m3，之后较长时间内保持恒定。若二者一起溃决，F水库漫顶不溃情况下(工况3)，淹没速度显著增大，溃坝约17 h后，L市的淹没面积和体积达最大值，分别约27 km2和1.1亿m3。

如果F水库上游2个坝体相继或同时发生溃决后，溃坝洪水导致F水库坝体也溃决，则不管是淹没速度还是最大淹没面积或体积都显著增大。在这3种工况(工况4—工况6)模式下，L市最大淹没面积达到时间、最大淹没面积和最大淹没水体分别约15 h，34 km2,1.28亿m3(工况4)；14.5 h，36 km2,1.41亿m3(工况5);13 h，47 km2,1.98亿m3(工况6)。在L市的淹没速度上，工况6也明显快于工况4和工况5。

考虑X水库溃决对L市的淹没影响时，如果F水库坝体在M水库和B水库坝体溃决时仅漫顶不溃决(工况7)，最大淹没发生的时间和面积及体积分别为14.5 h,88 km2,4.9亿m3。在M水库和F水库坝体的连溃(工况8)或是B水库和F水库坝体的连溃(工况9)2种工况下，L市的淹没程度相差不大，最大淹没面积约发生在M水库或B水库坝体溃坝约14 h后，最大淹没面积约94 km2，最大淹没水体约5.4亿m3。在最不利的所有坝体相继溃决的情况下(工况10)，L市最大淹没面积约发生在溃坝12 h后，最大淹没面积约102 km2，最大淹没水体约6.3亿m3。

5 结 语

从以上对某山区的H市及L市在上游各个坝体单溃或连溃条件下所受淹没历时、淹没面积和体积的分析中，可获得如下结论。

(1) 在单溃和连溃2种模式对下游城市淹没的影响分析中，本研究中所有工况都表明，相对于单溃而言，当上游梯级水库发生连溃时，其对下游城市的影响在淹没速度上更加迅速，在淹没面积和体积上更加宽广。

(2) 山区的坝体下游城市淹没速度和最大淹没面积主要与最大溃坝洪水流量相关。一般说来坝体越高，坝宽越大，溃坝时产生的瞬时最大流量越大，城市的淹没速度也就越快。不过对于承载多个不同来源方向水库洪水的城市而言，淹没速度和最大淹没面积还与水库和城市之间的距离相关。如工况4、工况5、工况7中，若讨论溃坝洪水对H市的影响，虽然工况7中X水库溃决时对H市的淹没面积大于工况4和工况5的情况，但由于工况4和工况5中H市上游坝体连溃导致的巨大溃坝流量在短时间内泄出，使得其淹没速度高于工况7。

(3) 山区城市的淹没历时主要与水库的容积相关，而与最大溃坝流量关系不大。本研究中所涉及的水库中，X水库体积最大，因此不管对于H市还是L市，只要X水库溃决，淹没历时将大大延长。对H市而言，溃坝发生60 h后，淹没面积才趋于恒定，对于L市而言则需要约69 h。值得注意的是，对工况10而言，虽然所有水库均发生溃决后，对城市的淹没速度非常快，最大淹没面积也非常大，但在达到最大淹没面积后，下降的过程也较其他工况(如工况8和工况9)更快，从而更早达到稳定淹没水平。

[1] 王延荣. 河南“75·8”特大洪水灾害[J]. 河南水利与南水北调，2013, (21): 35-39.

[2] 杜德进. 美国德里湖大坝溃决事故调查[J]. 大坝与安全，2011, (6): 46-51.

[3]RITTER A.The Propagation of Water Waves[J].Ver Deutsch Ingenieure Zeitschr,1892,36(33):947-954. [4] STOKER J J.Water Waves:Mathematical Theory with Application[M].Singapore:Wiley International Science,1958.

[5] 林秉南，龚振瀛，王连祥. 突泄坝址过程线简化分析[J]. 清华大学学报，1980, 20(1): 17-31.[6] 谢任之. 溃坝坝址流量计算[J]. 水利水运科学研究，1982, (1): 43-58.

[7] 符传君，练继建. 溃坝水流在复杂河道中传播的三维数值模拟[J]. 水利学报，2007, 38(10): 1151-1157.

[8] 曹志先，郑 力，钱忠东.溃坝水流三维湍流的试验与数值模拟[J].武汉大学学报(工学版)，2010, 43(2): 137-142.[9] 陈春燕，李远强，吴春耀，等. 梯级水库连续溃坝计算[J]. 广东水利水电，2011, (9): 40-42,46.

[10]宿 宾. 梯级水库溃坝计算及影响范围研究[J]. 河南水利与南水北调，2013, (24): 22-23.

[11]刘 林，常福宣，肖长伟，等. 溃坝洪水研究进展[J]. 长江科学院院报，2016, 33(6): 29-35.

[12]JARVIS A, REUTER H I, NELSON A,etal. Hole-filled Seamless SRTM Data V4, 2008 International Centre for Tropical Agriculture (CIAT) [EB/OL]. (2016-05-20) [2016-01-20] http://srtm.csi.cgiar.org.

[13]REUTER H I, NELSON A, JARVIS A. An Evaluation of Void Filling Interpolation Methods for SRTM Data[J]. International Journal of Geographical Information Science, 2007, 21(9): 983-1008.

[14]谢任之. 溃坝水力学[M]. 济南：山东科学技术出版社，1993.

(编辑：姜小兰)

Inundation Process of Downstream Cities byDam Break Flood from Cascade Reservoirs

YANG Zhong-yong1, GUO Hong-min1,2, CAO Guang-chun1
(1.College of Hydraulic and Environment Engineering, China Three Gorges University, Yichang 443002, China; 2.Collaborative Innovation Center for Geo-hazards and Eco-environment in Three Gorges Area, Yichang 443002, China)

The propagation of dam break flood and its influence on cities in the downstream are important issues indam safety research. In this paper, the inundation process of downstream cities were simulated and analyzed through numerical approach. A mountain river in south China with four cascaded reservoirs was selected as case study. The simulation was conducted with multiple dam break modes. Results suggest that the inundation speed and maximum inundated area are closely related to the maximum dam break discharge, i.e., related to the water head and size of the breach. The time required for maximum inundated area is related to the distance between city and reservoir. The speed as well as inundated area and inundated volume in the case of single break are less severe than those caused by successive cascaded break flood, which, however, floods and recedes dramatically. The duration of the inundation process for a city is related to the volume of the reservoir rather than to maximum break discharge.

cascade reservoirs; dam break flood; inundated area; dam break discharge; inundation duration

2016-06-12；

：2016-07-12

水利部公益性行业科研专项资助项目(201401027)

杨忠勇(1984-)，男，重庆忠县人，讲师，博士，主要从事大坝安全评估方面的研究，(电话)0717-6392644(电子信箱)ayong0710@163.com。

郭红民(1964-)，男，湖北宜昌人，教授级高级工程师，主要从事水力学及河流动力学方面的研究，(电话)0717-6392968(电子信箱)452507693@qq.com。

10.11988/ckyyb.20160594

2017,34(9):47-51,78

TV131

：A

：1001-5485(2017)09-0047-05