高陡边坡地震动放大效应分析

，，

(中国科学院 武汉岩土力学研究所，武汉 430071)

高陡边坡地震动放大效应分析

刘立波，李海波，刘亚群

(中国科学院 武汉岩土力学研究所，武汉 430071)

为了研究高陡岩质边坡对地震动加速度峰值的放大作用，分别针对简谐波和El Centro波竖向入射高陡边坡的情形，基于动力学模拟研究了坡肩和坡表面放大系数与坡高和坡比的参数关系。根据计算结果绘制边坡剖面的水平向和竖向放大系数等值线图，分析了坡体内放大系数分布特征。结果表明：放大系数并不随着坡高的递增而持续增大，放大系数的最大值出现在坡肩，在不超过2.0的范围内波动变化。坡顶面上的放大系数随着坡肩距的增大而逐渐衰减。坡体内水平向与竖向放大系数的空间分布特征显著不同，在邻近坡肩和斜坡面的区域内竖向放大系数可高达1.5，高陡边坡的抗震设计中不可忽略竖向放大系数的影响。

高陡边坡；地形放大效应；动力反应；放大系数；地震动参数

1 研究背景

大型水电工程中的岩质高边坡往往具有边坡高陡(属300 m级以上的超高边坡)、工程地质条件极为复杂的特点。锦屏水电站天然高边坡的坡高已超过1 000 m，小湾水电站的人工高边坡最大坡高约700 m，且天然高边坡的平均坡度大多在40°以上[1]。高陡边坡构成了水电工程的区域环境，地震作用下边坡的稳定性对工程结构的安全至关重要。

放大系数是指边坡的地震动加速度峰值与平坦地表面的加速度峰值之比。放大系数的影响因素众多，如局部地质条件、岩体力学特性和地震动作用等。由于目前积累的强震记录还很有限，尚难由强地面运动记录直接确定放大系数。边坡的振动台试验存在物理边界条件处理困难、费用高昂、试验结果差异较大等不足。因此，动力学数值模拟是当前研究高陡边坡放大效应的重要途径。

祁生文等[2]利用FLAC软件计算获得了高边坡坡体剖面的位移、速度和加速度的空间分布规律，分析了单面边坡的两种动力反应形式及临界高度。毕忠伟等[3]的计算发现，坡顶水平向和竖向加速度峰值分别约为输入的地震波加速度峰值的3倍和3.2倍，发生破坏后坡体位移存在变形累积效应。何蕴龙等[4]等利用水工规范推荐的反应谱进行了有限元计算，分析了均质岩体边坡地震动力系数的分布规律，研究了坡高、坡度和岩体动弹模量对岩体边坡地震动力系数的影响。郑文棠等[5]分析了某核电厂边坡的地震时程响应，得出地震作用下各向异性斜坡的自由面放大效应较各向同性斜坡强烈，更不利于边坡的抗震稳定，且放大效应随坡高增大而增大的结论。

我国建筑抗震设计规范[6]规定局部突出地形顶部的地震作用放大系数在1.1～1.6范围内取值。这一技术条文并未反映放大系数的空间分布规律，也不适用于高陡边坡。

目前对高陡边坡放大效应的机理研究和放大系数的规律分析尚不充分。本文分析了简谐波和地震波作用下坡肩和边坡表面放大系数的数值范围和变化规律，及其边坡剖面内的放大系数空间分布规律。这一研究工作可为高陡边坡的工程抗震设计提供技术参考。

2 边坡动力反应的计算模型

建立尽可能反映物理原型的计算模型是边坡动力反应分析的关键。动力学数值计算的直接目的是求解地震作用下边坡的S，V，A三个参数(即：位移S、速度V和加速度A)，再通过动力学分析的后处理来研究放大效应的规律。

2.1 计算模型的建立

地震作用下岩质高陡边坡动力反应分析的计算模型如图1所示。将坡体及其附近地基的部分包括在有限域的边坡模型中，而用外域模型代表无限大地质体。这样既可模拟近域中复杂的地形条件和岩体的变形破坏，又可模拟远域介质的无限延伸性和应力波向无限远域的逸散。数值模拟采用显式动力学数值计算软件LS-DYNA实现。

图1 计算模型示意图Fig.1 Schematic diagram of the calculation model

采用8节点六面体单元和映射网格划分边坡几何模型。有限单元网格在波传播方向上的尺寸通常在所考虑最短波长λ的1/12～1/8范围内取值[7]，采用单元尺寸为10 m的网格足以满足边坡动力反应分析的精度需求。

在地震荷载不足以诱发边坡破坏的前提下，线弹性本构关系适用于研究均质岩体边坡地震动放大效应。材料参数按照工程岩体分级标准[8]选取，详见表1。

表1 岩体材料参数Table 1 Material parameters of rock mass

近年来发展起来的完全匹配层(Perfectly Matched Layer,PML)方法具有精度高且算法易于实现的优点。PML方法最早由Berenger在解决电磁场的边界问题时引入，近年来也被应用到声波和应力波的传播问题研究中，被证明是目前最有效的人工边界条件处理方法。PML方法通过建立外域的有限单元网格模型和波传播解的数值算法来表征地震波向无穷远域的传播和逸散[9]。

本文的计算中，外域模型采用与边坡模型一致的单元类型和网格尺寸，网格单元通常需要5～10层且单元尺寸应足够小,以离散和吸收所有有意义的波长。PML方法是动力学边界条件的数值处理方法，计算得出的PML网格的节点位移、速度、加速度、应变等物理量的数值不具有实际的物理意义。因此，边坡计算模型尺寸的选取应将所有可能出现非线性变形的部分都纳入模型内部。依据PML方法的原理将远域模型最外层边界上的各节点位移约束为0，并不是施加动力学计算的位移荷载，而是限制位移的约束条件。

在边坡模型底部均匀分布的网格节点上施加时空一致的多点激励荷载，动荷载采用加速度形式的竖直向上入射的地震波。施加的动荷载需由地表指定的波形通过反演获得，才能与地表面的强地面运动相联系，如图1所示。施加的地震动荷载通过基于白噪声下动力反应分析的频域反演方法获得。

综合考虑动力学分析的精度需求、离散采样的频率折叠效应和计算机的数据存取效率等因素，本文动力学计算中以100 Hz的采样频率对边坡剖面内布设的采样点进行全时程采样。

2.2 放大系数的定义

由于坡脚处的加速度峰值通常略小于自由地表面的加速度峰值，故不宜以坡脚处的峰值作为基准值来计算放大系数。强震记录表明，一定区域范围内地表点的加速度峰值也往往差异较大[10]。以平坦自由地表面随意选定一点的加速度峰值作为基准也会引起放大系数计算结果的较大偏差。

(1)

式中NM为测点的个数。

水平向和竖向加速度峰值的放大系数分别定义为：

(2)

(3)

式中aH和aV分别为采样点的水平向和竖向加速度时间历程。

由上述公式可计算出边坡表面和坡体内任一位置(xi,yi,zi)的水平向和竖向的加速度峰值放大系数。汇总坡肩和边坡表面的放大系数计算结果，以分析放大系数依赖于参数的变化规律。依据采样点集的位置坐标和放大系数可绘制出边坡剖面内rV和rH的等值线图，以描述放大系数的空间分布特征。

3 SH简谐波入射高陡边坡

在地形放大效应的研究中，通常首先分析单一频率简谐波作用下边坡的放大系数。地震波是由多频率分量的谐波组成，但研究单一频率的谐波入射仍有理论价值。以竖向入射SH谐波进行分析。

3.1 坡肩的放大系数

针对坡比χ=4.0、坡高H介于100～1 200 m的高陡边坡，计算给出了1～5 Hz单一频率简谐波入射时,坡肩水平向放大系数随坡高的变化，如图2所示。

图2 坡肩水平向放大系数随坡高的变化Fig.2 Changes of horizontal amplification factor in slope crest with height

单一频率的谐波入射时，坡肩处的放大系数一般不超过1.8，坡肩处的放大系数并不随坡高的递增而持续增大，呈现出随坡高的递增在一定范围内波动变化的趋势。边坡的动力反应并未出现在特定频率谐波荷载作用下共振放大的情形。

3.2 坡体内放大系数的空间分布

不同频率简谐波下不同方向放大系数等值线见图3、图4。

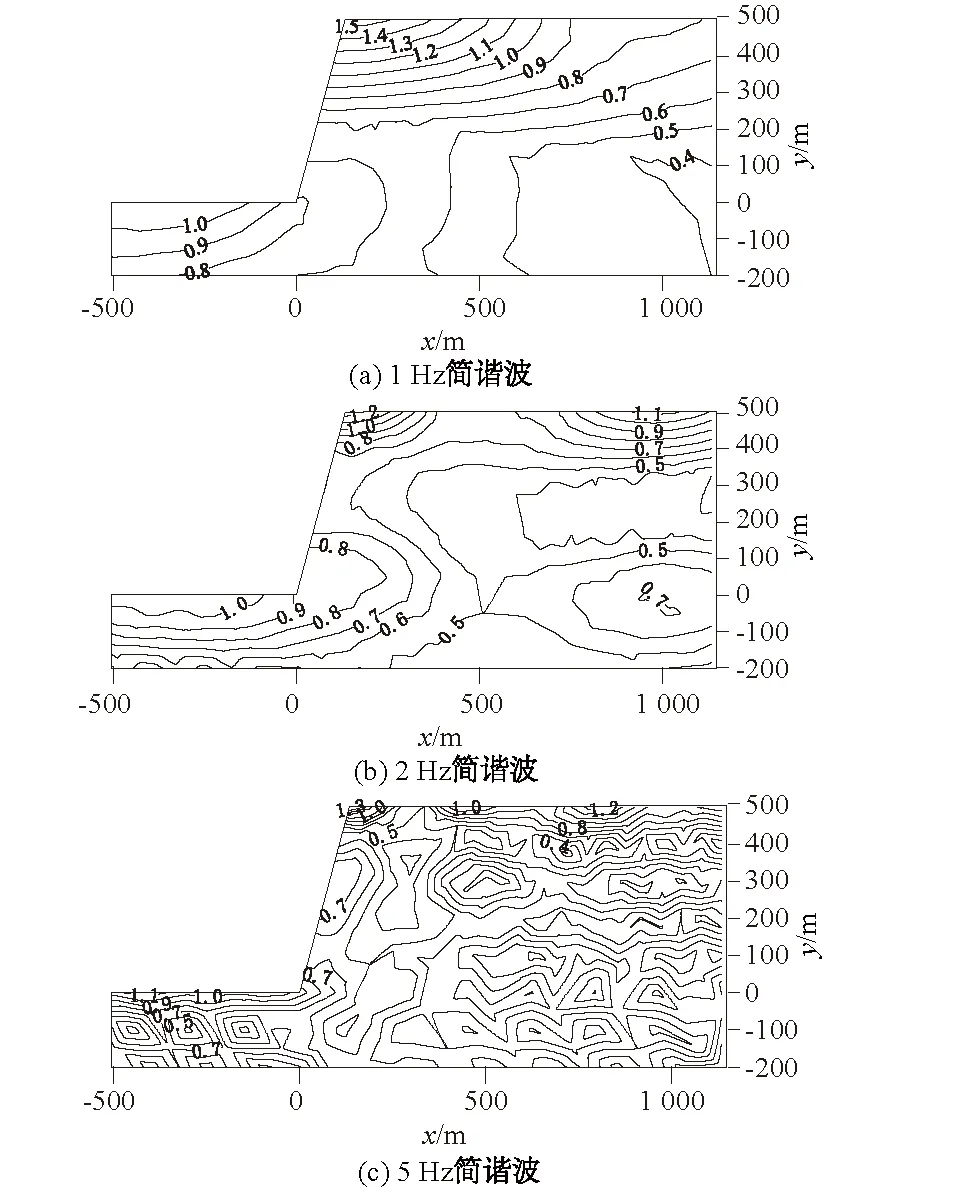
图3 不同频率简谐波下水平向放大系数等值线Fig.3 Isolines of horizontal amplification factor under different frequencies of harmonic wave

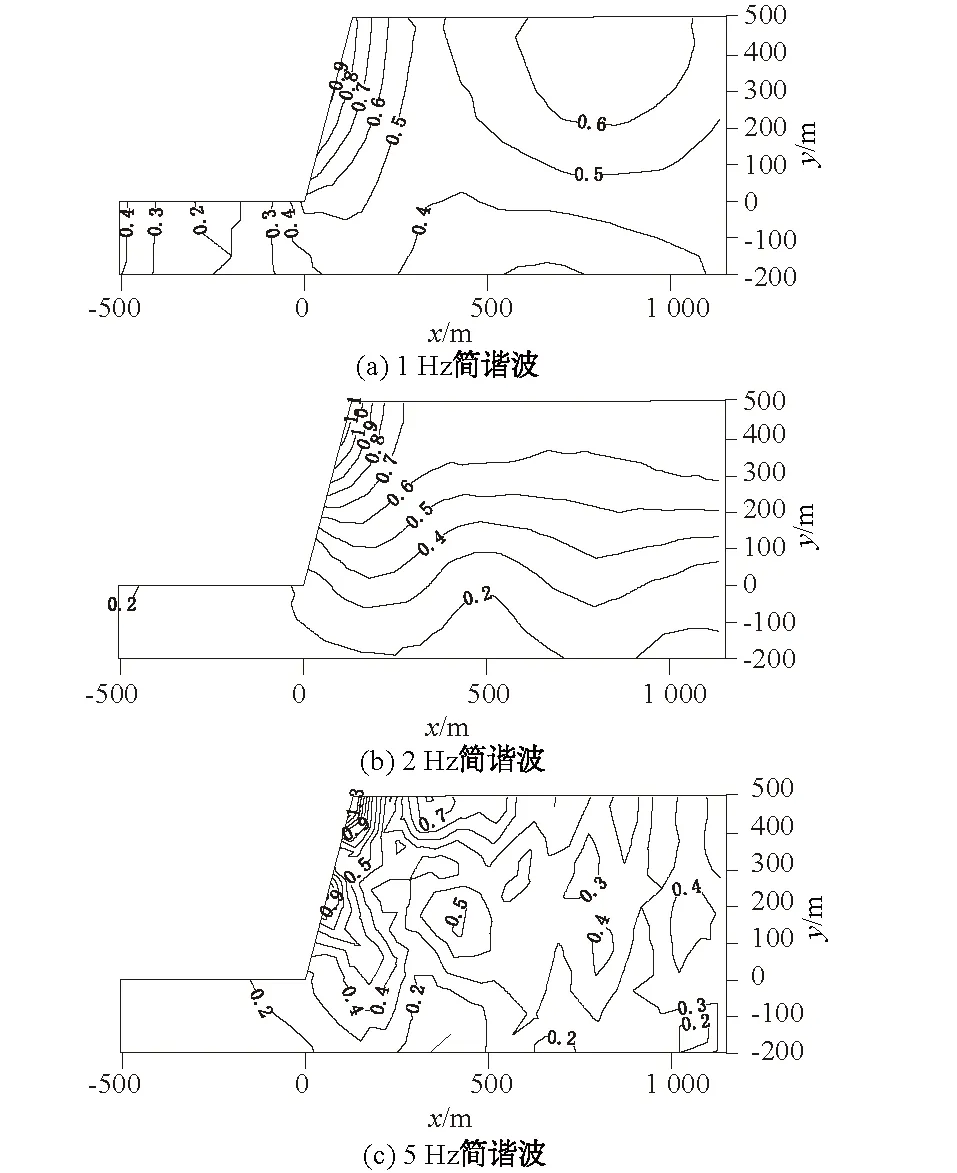
图4 不同频率简谐波下竖向放大系数等值线Fig.4 Isolines of vertical amplification factor under different frequencies of harmonic wave

坡肩处放大系数的规律并不能反映边坡剖面内放大系数的分布特征。如图3、图4中,随机选取坡高500 m，坡比4.0的Ⅱ级工程岩体的高陡边坡，以1，2，5 Hz的情形为例，依据计算结果逐一绘制了边坡剖面的放大系数等值线图。

更多的算例分析一致表明：简谐波竖向入射下，高陡边坡的水平向和竖向放大系数在邻近坡肩的区域内皆达到最大，但分布区域和分布特征有显著差异，这是由于不同频率谐波的波长不同和应力波反射后相位叠加的差异引起的。坡体内部的放大系数通常较小，斜坡面和坡顶面附近的放大系数随着深度的增加快速衰减，这不仅与应力波在自由面上的反射和叠加有关，还与表面波的影响有关。

4 地震波入射高陡边坡

放大系数与地震波波形和岩体材料参数的选取有关。这里以代表I级工程岩体的一组材料参数为例，在地表指定El Centro波，通过反演获得在计算模型底部施加的动荷载。通过动力学计算分析高陡边坡对地震动作用的放大效应。

4.1 坡肩的放大系数

首先分析坡肩放大系数与边坡几何参数(坡高和坡比)之间的关系。针对一组坡比系列(坡比χ为1.0，1.5，2.0，4.0，6.0)和一组坡高系列(坡高H在100～1 200 m之间)进行计算和分析。

不同坡比下坡肩的水平向放大系数详见图5。坡肩的水平向放大系数随坡比单调递增，且坡肩的放大系数最大不超过1.9。对各种不同坡比的边坡，坡肩的水平向放大系数并不随着坡高单调递增，而是随坡高的递增而在≤1.9的范围内波动。

图5 不同坡比下坡肩的水平向放大系数Fig.5 Horizontal amplification factor in slope crest under different gradients of slope

图6 坡肩不同方向的放大系数随坡高和坡比的变化Fig.6 Changes of horizontal and vertical amplification factors in slope crest with slope height and gradient

对相同坡高的边坡，坡肩放大系数随坡比的递增而增大；对比坡比χ=4.0与χ=6.0两组计算结果，坡肩放大系数却很接近。进一步的计算结果表明，当坡比χ≥4.0时，坡肩的放大系数几乎不再随坡比的递增而增大。

综合分析坡比和坡高这2个几何参数对高陡边坡坡肩处放大系数的影响，结果如图6所示。

由图6可见,坡比越大，坡肩处的水平向和竖向放大系数越大。无论是水平向还是竖向放大系数，都是随坡高的递增先逐渐增大，之后在一定范围内波动变化，但不超过2.0。

4.2 边坡表面的放大系数

下面分析边坡表面的水平向放大系数分布规律。

在平坦地表面、斜坡面和坡顶面布设采样点,以坡肩为参照位置，平坦地表面和斜坡面上的各测点与坡肩的水平距离为横坐标，标记在负半轴，而坡顶面的测点与坡肩的水平距离为横坐标，标记在正半轴，参见图1。

随机选取坡高300 m和700 m的情形计算和汇总坡表面各采样点的放大系数。其他坡高所反映的趋势和规律与此类似，故不赘述。对坡比介于1.0～6.0的5种情形分别绘制边坡表面放大系数的分布曲线，如图7所示。

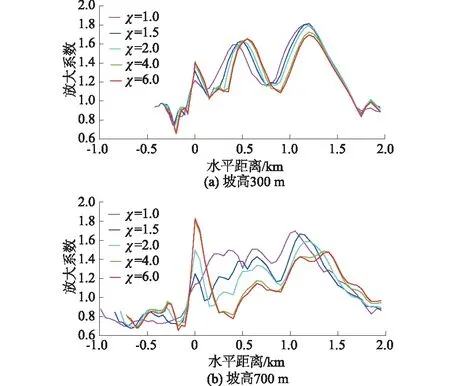
图7 边坡表面水平向放大系数的分布Fig.7 Horizontal amplification factor in the surface of slope

对相同坡高不同坡比的岩体边坡而言，边坡表面放大系数的随坡肩距的变化趋势是相似的。坡比χ=4.0和χ=6.0的曲线几乎重合，因此，对于χ≥4.0的情形放大系数不再增大。除了坡高300 m和700 m的情形之外，对其他坡高的更多计算结果也反映出与此一致的规律，故不予赘述。

4.3 坡体内放大系数的空间分布

通过分析坡体内放大系数分布的特征和规律，研究地震动作用下高陡边坡的地形放大效应。由于关注的是坡体主要区域内的放大系数分布，对坡比4.0的高陡边坡，选取坡高H=300 m和H=700 m的算例分别绘制坡体区域的水平向和竖向放大系数等值线图，如图8所示。

图8 不同方向和坡高下放大系数等值线Fig.8 Isolines of horizontal and vertical amplification factors under different slope heights

从图8可知，坡顶面的水平向放大系数随着深度增加而快速衰减，斜坡的竖向放大系数随着深度增加也呈现快速衰减的趋势。对高陡边坡而言，放大效应的影响主要体现在斜坡面、坡肩和坡顶面的邻近区域内，而在坡体内部，地震动加速度峰值并没有显著的放大。

5 结 论

通过对高陡边坡水平向和竖向放大系数的参数规律和空间分布特征的分析，发现地震动作用下的高陡边坡具有以下特性和规律：

(1) 坡体内应力波的反射、散射和叠加，以及边坡表面随深度剧烈衰减的表面波，是引起高陡边坡地震动放大效应的根本原因。放大系数并不随着坡高递增持续增大，而是在不超过2.0的范围内波动变化。

(2) 放大系数通常在坡肩处达到最大，坡顶面上的放大系数则随着远离坡肩距离的增大而逐渐衰减至1.0。水平向放大系数的最大值出现在坡肩和坡顶面的区域内。

(3) 对高陡边坡而言，放大效应的影响主要体现在斜坡面、坡肩和坡顶面的邻近区域内，坡体内部的地震动加速度峰值并没有显著的放大。

(4) 在邻近坡肩和斜坡面的区域内，竖向放大系数可高达1.5，在高陡边坡的抗震设计中不可忽略竖向放大系数的影响。

[1] 黄润秋. 岩石高边坡发育的动力过程及其稳定性控制[J]. 岩石力学与工程学报, 2008, 27(8):1525-1544.

[2] 祁生文，伍法权，孙进忠. 边坡动力响应规律研究[J]. 中国科学 E辑，2003，33(增1)：28-40.

[3] 毕忠伟，张 明，金 峰，等. 地震作用下边坡的动态响应规律研究[J]. 岩土力学，2009，30(增1)：180-183.

[4]何蕴龙，陆述远. 岩石边坡地震作用近似计算方法[J]. 岩土工程学报，1998，20(2)：66-68.

[5] 郑文棠，程小久，李焯芬，等. 核电厂边坡地震动力响应研究[J]. 岩石力学与工程学报，2011，30(增2)：3514-3521.

[6] GB 50011—2010，建筑抗震设计规范[S]. 北京：中国建筑工业出版社，2010.

[7] GB 17741—2005，工程场地地震安全性评价[S]. 北京：中国标准出版社，2005.

[8] GB 50218—94， 工程岩体分级标准[S]. 北京：中国计划出版社，1995.

[9] BASU U, CHOPRA A K. Perfectly Matched Layers for Transient Elastodynamics of Unbounded Domains[J]. International Journal for Numerical Methods in Engineering，2004，59(8)：1039-1074.

[10]ASSIMAKI D, GAZETAS G, KAUSEL E. Effects of Local Soil Conditions on the Topographic Aggravation of Seismic Motion: Parametric Investigation and Recorded Field Evidence from the 1999 Athens Earthquake[J]. Bulletin of the Seismological Society of America, 2005, 95(3): 1059-1089.

(编辑：王 慰)

Ground Motion Amplification Effect of High and Steep Slopes

LIU Li-bo，LI Hai-bo，LIU Ya-qun
(Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China)

In this article, dynamics numerical simulations are conducted to investigate the amplification of peak ground acceleration of high-steep rock slope. The relations of amplification factors in the crest and surface of slope with the height and gradient of slope are studied in the presence of harmonic wave and El Centro seismic wave. According to the computation results, the isolines of horizontal and vertical amplification factor of cross-sectional slope are plotted to analyze the amplification factor distribution in slope. Results indicate that amplification factor does not continuously increase with the rise of slope height. The maximum amplification factor appears in the crest of slope, and fluctuates in a range of no more than 2.0. Amplification factor in the top surface of slope gradually decreases as the distance from slope crest increases. The spatial distribution characteristics are markedly different between horizontal and vertical amplification factors in the slope. In the area near the crest of slope, vertical amplification factor is up to 1.5. The influence of vertical amplification factor cannot be ignored in the seismic design of high and steep slope.

high and steep slope; topographic amplification effect; dynamic response; amplification factor; ground motion parameter

2016-05-10；

：2016-06-06

国家杰出青年科学基金项目(51025935)

刘立波(1985-)，男，甘肃甘谷人，工程师，博士，研究方向为岩土动力学，(电话)18627012685(电子信箱)lzucas@163.com。

10.11988/ckyyb.20160451

2017,34(9):98-103

TU452

：A

：1001-5485(2017)09-0098-06