WA-BT-ELM耦合模型在黄土滑坡位移预测中的应用
2017-09-15,,,,,
, ,, ,,
(1.成都理工大学 地质灾害防治与地质环境保护国家重点实验室,成都 610059;2.山东大学(威海) 数学与统计学院,山东 威海 264209; 3.爱荷华大学 智能系统研究实验室,美国 爱荷华州 爱荷华城 52242-1527)
WA-BT-ELM耦合模型在黄土滑坡位移预测中的应用
李骅锦1,许强1,王思澄2,亓星1,彭大雷1,何雨森3
(1.成都理工大学 地质灾害防治与地质环境保护国家重点实验室,成都 610059;2.山东大学(威海) 数学与统计学院,山东 威海 264209; 3.爱荷华大学 智能系统研究实验室,美国 爱荷华州 爱荷华城 52242-1527)
黄土滑坡的变形演化过程往往受到多种因素的影响,呈现出非线性特征。基于小波分析函数(Wavelet Analysis,WA)、提升回归树(Boosting Regression Tree,BT),以及极限训练机(Extreme Learning Machine,ELM)方法,提出一种名为WA-BT-ELM的黄土滑坡位移预测新方法。该方法将非线性位移数据作为一时间序列,运用小波分析函数将监测点累积位移曲线分解为若干子小波;随后使用提升回归树对所有子小波进行重要度分析,剔除相关性不高的子小波以去掉冗杂信息;最后运用极限训练机,结合筛选得到的子小波对滑坡位移进行预测分析。基于该模型对甘肃省永靖县黑方台滑坡区的滑坡位移监测数据进行预测,得到了优于ANN,BPNN,SVM,ELM,以及WA-ELM预测模型的结果,故认为WA-BT-ELM模型是一种有效的黄土滑坡位移预测方法。
黄土滑坡;WA-BT-ELM耦合模型; 位移预测;小波变换;提升回归树;极限训练机
1 研究背景
黄土滑坡是一种较为常见并且危害较大的地质灾害,现在已经成为黄土地区一类关注度极高的地质环境问题。与其他岩土质滑坡相比,黄土滑坡没有明显的滑动面,加之其发生频率高,致灾机理复杂,发生前兆不明显等特点,使得黄土滑坡预测工作难以开展[1]。
广义上的滑坡,其变形演化过程受到坡体自身因素与外部因素的共同影响,位移监测数据往往出现与之对应的非线性变化特征[2]。所以在实际滑坡预测中,直接根据滑坡累积位移曲线分析与预测滑坡变形[3],很容易得到错误结果。滑坡变形监测系统的非线性和不确定性使滑坡预测变得复杂[4-6],黄土滑坡也不例外。
随着科学技术的发展,不少数据挖掘方法被运用到滑坡预测中。比如Pouzols等[7]在2010年运用Auto-regressive 模型回归模拟,可以对滑坡位移进行预测;Kayacan等[8]在2010年运用The Gray System模型,可以从概率统计的角度寻找位移数据内在联系,进行预测;Ran等[9]在2010年运用BP神经网络(BP Neural Network,BPNN)模型,通过训练前期样本获得数据网络,进行预测。更加前沿的数据挖掘方法如支持向量机[2,10](Support Vector Machines,SVM)、指数平滑模型[11](Exponential smoothing model,ESM)、Verhulst模型[12]等也被运用到滑坡位移预测中。虽然上述研究取得了一定的成果,但由于各种方法有其自身的优势以及局限,因此采用一种切实可行的方法对黄土滑坡进行位移预测显得十分迫切。
近年来,一种高效的单隐含层前馈神经网络学习算法,称作极限训练机的算法被提出[13-15]。该算法具有需要的数学模型简单、学习速度快、能获得全局最优解、对新样本的适应性强的优势[14,16-17]。基于这些优势,该方法已经在能源[18]、人脸识别[19-20],以及银行领域[21]等行业运用,并且取得了较好的效果。
为了提高位移监测数据预测模型的精度,需要合理分解滑坡累计位移信号分类别针对性处理。小波分析函数是一种不需要先验知识就可以处理具有随机性且变化趋势复杂数据的方法[22],目前已经有相关研究证明了小波函数用于滑坡变形预测的可行性[22-23]。
在所有滑坡累计位移信号中,也含有一些冗杂信息因子。如果将所有信号作为输入特征,会使得预测模型过于复杂,并且冗杂因子还会干扰模型预测决策,降低模型泛化能力。相关研究[24]表明,提升回归树能对数据进行精简,剔除冗杂信息,获得核心因子。
本文基于“分解与合并”思想[2,25-26],结合上述前人研究成果,针对黄土滑坡位移影响因素繁多和位移过程复杂的特点,结合小波分析函数(Wavelet Analysis,WA)、提升回归树(Boosting Regression Tree,BT),以及极限训练机(Extreme Learning Machine,ELM)方法,组合形成WA-BT-ELM的新方法对黄土滑坡位移监测数据进行预测分析,并结合甘肃省永靖县黑方台滑坡区的滑坡位移监测数据对模型预测效果进行分析评价。
2 预测方法简介
由于黄土滑坡规模一般不太大,兼顾滑坡崩塌的特点,加之其具有发生的高频性、致灾机理的复杂性、发生前兆的模糊性等特点,使得其预测工作开展难度较高。黄土滑坡的位移变形量在一定时期内也是微小的,真实位移数据信号相对较弱,容易受到系统误差的干扰。为了提高预测的精度,本文基于小波分析函数、提升回归树,以及极限训练机方法,提出一种新的黄土滑坡位移预测方法。该方法基本步骤为:以实测滑坡位移监测数据为基础,运用小波分析函数将监测点累积位移曲线分解为若干子小波 (Sub-wavelet,B-W),得到不同频域的位移信号;随后使用提升回归树对所有子小波与原始监测数据的重要度进行排序,剔除相关性不高的子小波以去掉冗杂信息,尽可能排除误差噪点;随后选择重要度较高的子小波 (Highly-important Sub-wavelet,HB-W)作为模型的初始输入,运用极限训练机对滑坡位移进行预测。其方法具体流程详见图1。下文详细介绍小波分析、提升回归树和极限训练机的具体操作步骤。
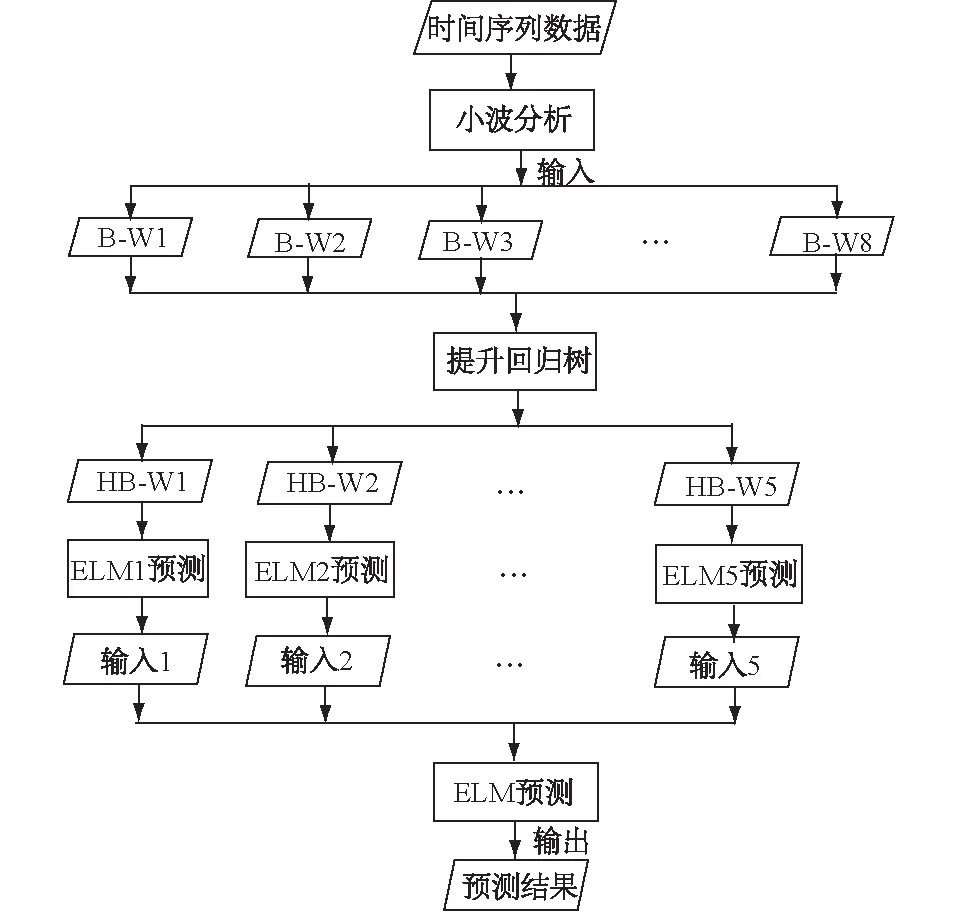
图1 预测方法流程Fig.1 Flowchart of the model
2.1 小波分析
小波分析具有良好的时频特性和多分辨率特性,是一种窗口大小恒定、形态可变的时频局部信号分析方法[27]。基于小波具有震荡性、能够迅速衰减归零的特性,通过伸缩平移计算,对信号进行多维细化,全方位获得信号的细节[22]。本文将滑坡在不同时间的变形值作为单一时间序列,运用小波分析对该位移序列进行分解,得到可靠的多维细化信号。
小波分析的基本原理是用一个基函数的平移和伸缩来分解L2(R)空间的函数[28]。设基函数满足容许条件:
(1)
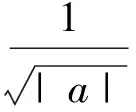
(2)
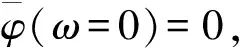
将基本小波经过伸缩平移,得到子小波为
(3)
2.2 提升回归树
提升回归树是一种能自我调整适应的集成学习算法,能利用归纳算法生成的可读规则对数据进行分析,达到对数据分类的目的。区别于传统统计分类方法,提升回归树并不是单一寻找最优模型组合,而是通过大量相对简单的决策树方法优化模型性能,得到最优的模型结果的方法[29]。本文运用提升回归树,将多维细化信号进行重要度排序,去除冗杂信息。模型形式为
(4)
式中:X是预测变量;Tn(X,γn)是第n株分类回归树;γn为分类回归树参数,代表树中分裂点与叶子节点的赋值。
2.3 极限训练机
极限训练机是Huang等[14]基于单隐含层前馈神经网络提出的一种简单高效的算法。其输出函数表达式为
(5)
式中:L为隐含层神经元数;ai和bi为隐含层节点参数;βi表示连接第j个隐含层和网络输出之间的外权;G(ai,bi,x) 表示第j个隐含层对应于样本x的隐含层节点输出,与激发函数g(x)的关系为
G(ai,bi,x)=g(aix+bi) 。
(6)
其中:g:R→R为激活函数;aix代表内权向量ai和样本x在Rn中的内积。
考虑任意N个互异的数据样本{(xi,ti)}Ni=1∈Rn×Rm,如果存在一个含有L个隐含层神经元的单隐含层神经网络,可以零误差逼近这N个互异的数据样本,则存在ai,bi和βi,i=1,2,…,L使得
Hβ=T。
(7)
其中:H为隐含层输出矩阵,
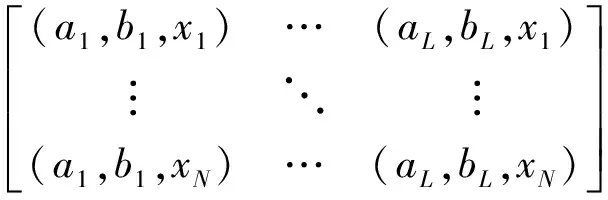

其中β通过最小二乘法进行求解,即
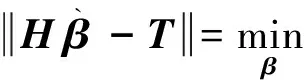
‖Hβ-T‖ 。
(8)
在隐含层输出为列满秩的条件下,利用Moore-Penrose广义逆[30-31]可以得到
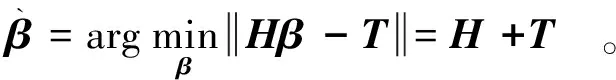
(9)
其中H+=(HTH)-1HT。而当隐含层输出层矩阵非列满秩的情况,最优外权β可以利用奇异分解[32]的方法得到。
而ELM激发函数[14]形式为
(10)
在训练过程中,算法随机确定隐含层节点参数。通常在实际运算过程中,样本数据经过了标准化处理,隐含层节点参数值往往在 [-1,1] 内随机选择,可简化训练过程。ELM网络学习过程大致见图2。
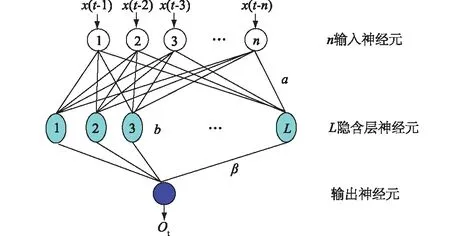
图2 ELM结构示意图Fig.2 Structure of extreme learning machine(ELM)
3 实例应用
为验证本文提出的黄土滑坡位移预测新方法的有效性以及准确性,取甘肃省永靖县黑方台滑坡区的滑坡位移监测资料,对模型的预测效果进行分析评价。
3.1 研究区概述
黑方台滑坡区位于中国甘肃省永靖县盐锅峡水库下游,距兰州市西约45 km ,距永靖县城北约20 km。黑方台面积约11.5 km2,位于盐锅峡镇附近的虎狼沟将其切割成2部分,方台位于南西侧,面积为1.7 km2,黑台位于北东侧,面积约9 km2。研究区位于祁吕贺山字型构造与陇西旋转构造的复合部位,区域构造活动以差异上升为主,伴随着黄河常年的侵蚀,形成显著的阶地地貌,且沟壑发育强烈。黑方台地区属于黄河Ⅳ级阶地,原本是一处十分荒芜的黄土塬。1968年,为了安置刘家峡、盐锅峡库区的移民,在台塬上建成了规模较大的提水灌溉工程,10 a后,黑方台地区滑坡灾害进入高发期。目前,沿黄土塬边一共发育75处滑坡,俯瞰位于黄河Ⅰ级阶地的居民区(见图3),威胁着当地百姓的生命财产安全。

图3 研究区滑坡群与GPS监测点位置示意图Fig.3 Distribution of landslides and GPS location in the study area
3.2 数据来源
为了有效减少滑坡带来的灾害,在研究区选取典型滑坡,安装GPS位移监测系统。如图3所示,在滑坡区布设了8个GPS监测点,其中GPS0为静点,其他7个点为动点。位移监测数据通过坐标换算,得到其与监测滑坡主滑方向一致的位移值。由于GPS5数据变化较大,展现出较强的非线性特点,选5号GPS监测点作为研究特征点,取该点2014年12月26日至2015年12月21日约12个月的监测数据,检验本文建立模型的可靠性与准确性。
3.3 模型结果
非线性位移数据作为一时间序列,输入与输出变量均是某一时刻滑坡位移值。由于黄土滑坡规模一般不大,所以其位移变形量在一定时期内也是微小的,其监测位移信号表现为一种弱信号,所以系统误差会表现为强信号噪点。为了在强噪点干扰下的序列数据中提取精确可靠的变形特征信息,首先运用小波分析函数对监测位移数据各频率成分进行分解,得到不同分辨率的位移信号。本文选取Haar小波,分解层数为3层。图4展示原始监测数据与小波模型得到的8个子小波(Sub-wavelet,B-W)。
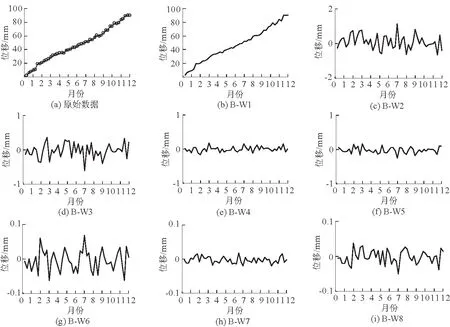
图4 原始数据与小波分析模型结果Fig.4 Observed displacement data and all the sub-wavelets
为了对位移监测数据进行精确预测分析,需要对所有分辨率情况下的位移信号进行相关性分析,探究子小波与原始位移的相关性排序情况以剔除冗杂信息。本文运用提升回归树计算各个子小波与原始位移数据之间的重要度,模型计算结果详见表1。分析表1可知,所有子小波与原始监测数据均有一定的重要度。B-W1,B-W2,B-W3,B-W4和B-W5与原始监测数据之间的重要度均>0.600,体现出较高的重要度;而B-W6,B-W7和B-W8与原始监测数据之间的重要度分别为0.476,0.407,0.397,均<0.600,体现出较低的重要度。所以本文选择重要度较高的5个小波为高重要度的子小波 (Highly-important Sub-wavelet,HB-W),分别为HB-W1,HB-W2,HB-W3,HB-W4和HB-W5。
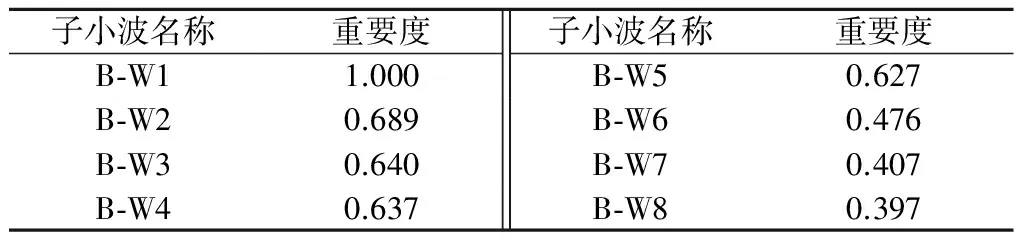
表1 子小波与原始监测数据相关性Table 1 Degree of the importance of all the sub-wavelets to the original observed displacement data

图5 重要度较高的子小波ELM预测模型结果Fig.5 ELM prediction results of the highly important sub-wavelets
随后,以时间点为输入序列,以重要度较高的子小波为目标序列,分别建立ELM1,ELM2,ELM3,ELM4,ELM5模型。模型得到了高重要度子小波的预测值,是接下来整体位移预测的基础,预测结果详见图5。由图5可知,高重要度的子小波ELM模型均成功完成预测。由于ELM4,ELM5预测所选子小波数值较小,微小的残差即会引起较大的百分误差,从而影响预测的效果,但是这2组模型的相关系数仍然达到了0.878 1和0.843 1。小波数值较大的ELM1,ELM2,ELM3模型相关系数更是达到了0.989 1,0.967 6,0.910 7。综上分析可知,5种ELM预测值与子小波的相关系数均超过了0.80,均为显著相关,模型取得了良好的结果。
根据前文结果,建立以高重要度的子小波ELM模型结果为输入序列、位移监测数据为目标序列的ELM模型。预测结果详见图6。
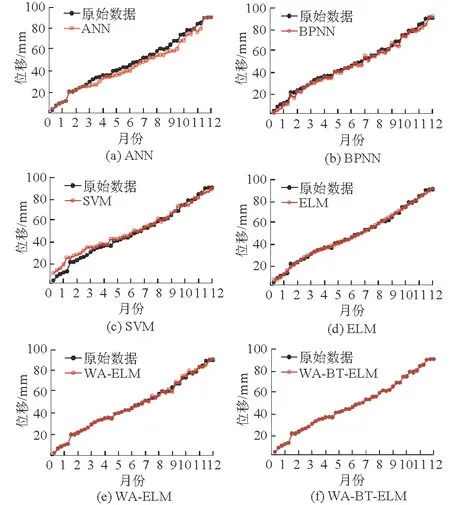
图6 模型预测结果Fig.6 Prediction results of all the models above mentioned
4 结果分析
基于图6数据,比较WA-BT-ELM方法与传统方法,即人工神经网络(Artificial Neural Network,ANN),后向型神经网络(Back Propagation Neural Network,BPNN),SVM,ELM,以及WA-ELM方法,发现WA-BT-ELM方法在可靠性与准确性上均有提高(结果见表2)。模型精度检验常用到均方根误差(RMSE,需对数据进行归一化处理[13-14])、平均绝对误差(MAE),以及平均绝对百分误差(MAPE),计算式如下:
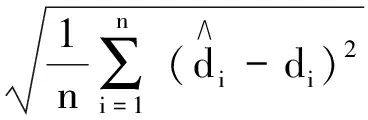
(11)

(12)
(13)
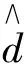

表2 模型结果评价参数Table 2 Evaluation parameters of the results ofdifferent models
分析表2评价参数可知,由于本文选择监测数据在数值上偏小,所以各个模型的误差参数值均不大。分析这6种模型结果,WA-ELM与WA-BT-ELM模型返回的均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分误差(MAPE)均小于其他模型,体现了组合模型的优势。但是WA-ELM模型的最大残差值为4.091 8 mm,在这6种模型中优势并不明显,说明监测位移信号中的冗杂信息对最后的预测结果产生了干扰。而WA-BT-ELM模型的最大残差值为0.887 1 mm,远远小于其他5种模型的返回值。针对黑方台滑坡监测数据,本文认为WA-BT-ELM是一种优于ANN,BPNN,SVM,ELM,以及WA-ELM的方法,能有效提高黄土滑坡位移预测的可靠性与准确性,是一种有效的黄土滑坡位移预测方法。
5 结 论
本文基于小波分析函数,提升回归树,以及极限训练机,提出一种黄土滑坡位移预测新方法WA-BT-ELM。针对黄土滑坡位移变化较小,容易受到系统误差干扰的特点,该模型运用小波函数和提升回归树模型,剔除了重要度不高的子小波,并运用极限训练机进行位移预测。其预测结果与ANN,BPNN,SVM,ELM,以及WA-ELM方法进行对比,发现该模型的RMSE,MAE,MAPE和最大残差均优于其他模型。而且极限训练机是一种单隐含层前馈神经网络,模型在训练网络的过程中只需要设置隐藏神经元个数,操作简便,同时减少了人为干预。综上分析可知,WA-BT-ELM模型能有效地提高黄土滑坡位移预测的精度,为黄土滑坡位移预测提供了一种新的方法,能够在黄土滑坡位移预测领域中发挥一定的作用。
[1] 李骅锦,许 强,何雨森,等. 甘肃黑方台滑坡滑距参数的BP神经网络模型[J]. 水文地质工程地质,2016, 43(4):141-146,152.
[2] 李骅锦,许 强,何雨森,等. WA联合ELM与OS-ELM的滑坡位移预测模型[J]. 工程地质学报,2016, 24(5):721-731.
[3] 李 强,李端有. 滑坡位移监测动态预报时间序列分析技术研究[J]. 长江科学院院报,2005, 22(6):22-25.
[4] QIN S Q, JIAO J J, WANG S J. The Predicable Time Scale of Landslides[J]. Bulletin of Engineering Geological Environment, 2001, 59(4):30-312.[5] 陈卫兵,李端有. 基于非线性动力学的滑坡位移预测[J]. 长江科学院院报,2006, 23(2):28-30,34. [6] 杨建国,晏鄂川,程温鸣. 滑坡变形特征的GPS监测信息识别研究[J]. 长江科学院院报,2012, 29(3):24-28.
[7] POUZOLS F M, LENDASSE A, BARROS A B. Autoregressive Time Series Prediction by Means of Fuzzy Inference Systems Using Nonparametric Residual Variance Estimation[J]. Fuzzy Sets System, 2010, 161(4):471-497.
[8] KAYACAN E, ULUTASB B, KAYNAKA O. Grey System Theory-based Models in Time Series Prediction[J]. Expert System Application, 2010, 37(2):1784-1789.
[9] RAN Y F, XIONG G C, LI S S,etal. Study on Deformation Prediction of Landslide Based on Genetic Algorithm and Improved BP Neural Network[J]. Kybernetes: The International Journal of Systems & Cybernetics, 2010, 39(8):1245-1254.
[10]LIU Z, SHAO J, XU W,etal. Comparison on Landslide Nonlinear Displacement Analysis and Prediction with Computation Intelligence Approaches[J]. Landslides, 2013, 11(5):889-896.
[11]尹光志, 张卫中, 张东明, 等. 基于指数平滑法与回归分析相结合的滑坡预测[J]. 岩土力学, 2007, 28(8): 1725-1728.
[12]LI X Z, KONG J M, WANG Z Y. Landslide Displacement Prediction Based on Combining Method with Optimal Weight[J]. Natural Hazards, 2012, 61(2): 635-646.
[13]HUANG G B, CHEN L, SIEW C K. Universal Approximation Using Incremental Constructive Feed Forward Networks with Random Hidden Nodes[J]. IEEE Transactions on Neural Network, 2006, 17(4): 879-892.
[14]HUANG G B, ZHU Q Y, SIEW C K. Extreme Learning Machine: Theory and Applications[J]. Neurocomputing, 2006, 70(1-3):489-501.
[15]ZHU Q Y, QIN A K, SUGANTHAN P N,etal. Evolutionary Extreme Learning Machine[J]. Pattern Recognition, 2005, 38(10):1759-1763.
[16]HUANG G B. Learning Capability and Storage Capacity of Two-hidden-layer Feed Forward Networks[J]. IEEE Transactions on Neural Network, 2003, 14(2):274-281.
[17]HUANG G B, BABRI H A. Upper Bounds on the Number of Hidden Neurons in Feed Forward Networks with Arbitrary Bounded Nonlinear Activation Functions[J]. IEEE Transactions on Neural Network, 1998, 9(1):224-229.
[18]OUAMMI A, DAGDOUGUI H, SACILE R,etal. Monthly and Seasonal Assessment of Wind Energy Characteristics at Four Monitored Locations in Liguria Region (Italy)[J]. Renewable and Sustainable Energy Reviews, 2010, 14(7):1959-1968.
[19]MICHE Y, AKUSOK A, VEGANZONES D,etal. SOM-ELM-Self-Organized Clustering Using ELM[J]. Neurocomputing, 2015, 165(1):238-254.
[20]ZONG W W, HUANG G B. Face Recognition Based on Extreme Learning Machine[J]. Neurocomputing, 2011, 74(16): 2541-2551.
[21]YU Q, MICHE Y, SEVERIN E,etal. Bankruptcy Prediction Using Extreme Learning Machine and Financial Expertise[J]. Neurocomputing, 2014, 128(27):296-302.
[22]REN Fu, WU Xue-ling, ZHANG Kai-xiang,etal. Application of Wavelet Analysis and a Particle Swarm-optimized Support Vector Machine to Predict the Displacement of the Shuping Landslide in the Three Gorges, China[J]. Environmental Earth Sciences, 2015, 73(8):4791-4804.
[23]KAUNDA R B. A Linear Regression Framework for Predicting Subsurface Geometries and Displacement Rates in Deep-seated, Slow-moving Landslides[J]. Engineering Geology, 2010, 114(1/2):1-9.
[24]HE Y, KUSIAK A, OUYANG T,etal. Data-driven Modeling of Truck Engine Exhaust Valve Failures: A Case Study[J]. Journal of Mechanical Science and Technology, 2017, 31(6): 2747-2757.
[25]YU L, WANG S Y, LAI K K. Forecasting Crude Oil Price with an EMD-based Neural Network Ensemble Learning Paradigm[J]. Energy Economics, 2008, 30(5):2623-2635.
[26]GUO Z H, ZHAO W G, LU H Y,etal. Multi-step Forecasting for Wind Speed Using a Modified EMD Based Artificial Neural Network Model[J]. Renewable Energy, 2012, 37(1):241-249.
[27]SAMAR V J, BOPARDIKAR A, RAO R,etal. Wavelet Analysis of Neuroelectric Waveforms: A Conceptual Tutorial[J]. Brain and Language, 1999, 66(1):7-60.[28]CHELLALI F, KHELLAF A, BEELOUCHRANI A. Wavelet Spectral Analysis of the Temperature and Wind Speed Data at Adrar,Algeria[J].Renewable Energy,2010,35(6):1214-1219.[29]SOYKAN C U, EGUCHI T, KOHIN S,etal. Prediction of Fishing Effort Distributions Using Boosted Regression Trees[J]. Ecological Applications, 2014, 24(1):71-83.
[30]RAO C R, MITRA S K. Generalized Inverse of Matrices and Its Applications[M]. Baltimore and London: John Wiley and Sons, 1971.[31]SERRE D.Theory and Applications[M].New York:Springer,2002.
[32]ORTEGA J M. Matrix Theory[M].New York and London:Plenum Press, 1987.
(编辑:陈 敏)
Application of a Novel Predictive Model Integrating Wavelet Analysis,Boosting Regression Tree and Extreme Learning Machine toLoess Landslide Displacement
LI Hua-jin1,XU Qiang1,WANG Si-cheng2,QI Xing1,PENG Da-lei1,HE Yu-sen3
(1.State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China;2.School of Mathematics and Statistics, Shandong University, Weihai 264209, China; 3.Intelligent Systems Laboratory, Seamans Center, Mechanical and Industrial Engineering, The University of Iowa, Iowa City 52242-1527, U.S.A.)
The deformation evolution process of loess landslide is often nonlinear due to many factors. A theoretical approach named WA-BT-ELM, which is based on wavelet analysis (WA), boosting regression tree (BT) and extreme learning machine (ELM), is proposed to predict loess landslide displacements. By analysis of nonlinear loess landslide time-dependent displacement dataset, the accumulation displacement data signal is decomposed into a series of sub-wavelets. Then, the importance of all the sub-wavelets to the displacement data series is computed by BT algorithm. The highly important sub-wavelets are selected to make further predictions. Furthermore, the predictive results of sub-wavelet and the original landslide displacement series are obtained through ELM algorithms. A case study of Heifangtai landslide in Gansu Province is presented to verify the predictive results. In comparison, the predictive results by using WA-BT-ELM model is faster and more accurate than those by ANN,BPNN,SVM,ELM and WA-ELM model, indicating that the WA-BT-ELM model is effective in loess landslide displacement prediction cases.
loess landslide; WA-BT-ELM model; displacement prediction; wavelet analysis; boosting regression tree; extreme learning machine
2016-05-26;
:2016-06-29
国家重点基础研究计划(973计划)资助项目(2014CB744703);国家杰出青年科学基金项目(41225011);教育部“长江学者奖励计划”项目( T2011186)
李骅锦(1991-),男,四川达州人,硕士研究生,主要从事地质灾害预测评价与防治处理的研究,(电话)18782959226(电子信箱)286069283@qq.com。
10.11988/ckyyb.20160529
2017,34(9):63-69
P642.22
:A
:1001-5485(2017)09-0063-07
