一类时滞SLARS网络病毒传播模型的周期解

赵 涛，魏苏林，齐子健，张子振

（安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030）

一类时滞SLARS网络病毒传播模型的周期解

赵 涛，魏苏林，齐子健，张子振

（安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030）

文章研究了一类具有分级感染率的时滞SLARS网络病毒传播模型。以模型的时滞为分岔参数，确定了产生Hopf分岔的时滞临界点；利用中心流形定理和规范型理论确定了在时滞临界点处产生的Hopf分岔的性质。

SLARS模型；时滞；Hopf分岔；周期解

0 引言

由于网络病毒具有诸如破坏性、多态性以及不可预知性等典型特征，已经成为我们工作和日常生活最大的威胁之一[1-2]。对网络病毒传播过程进行动力学建模，是了解网络病毒行为的一种有效方法。近年来，不少网络病毒传播模型被国内外学者相继研究，并取得了一定的研究成果，如，SEIR模型[3-4]，SEIRS模型[5-6]，SEIQRS模型[7-8]等。但是以上具有潜伏状态的网络病毒传播模型，大多都是假设潜伏状态的主机不具备感染能力，并且考虑网络病毒传播过程中的时滞因素的也较少。最近，文献[9]研究了如下潜伏状态和活跃状态主机均具有感染能力的时滞SLARS网络病毒传播模型：

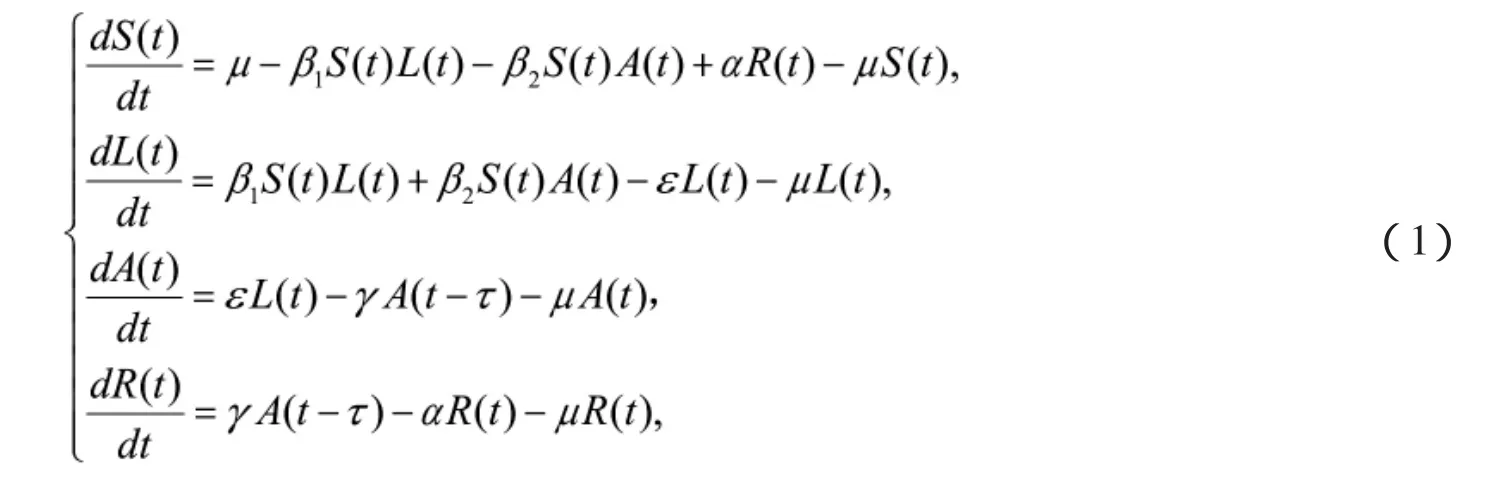
其中，S(t)，L(t)，A(t)和R(t)分别表示易感主机、处于潜伏状态的主机、处于活跃状态的主机以及处于恢复状态的主机在t时刻所占的比例。μ为外部主机的联网率和内部主机的断网率；β1和β2分别为处于潜伏状态的主机和处于活跃状态的主机的感染率；α，ε和γ分别为状态转移率。为反病毒软件查杀网络病毒所需要的时间周期。

文献[9]以反病毒软件查杀网络病毒所需要的时间周期所引起的时滞为分岔参数，研究了模型（1）的有病毒平衡点的局部渐近稳定性和局部Hopf分岔的存在性。对于一个动力系统模型而言，其动力学性质除了稳定性以外，还有持续性[10]，周期解[11]以及全局吸引性[12]等性质。本文在文献[9]的基础上，研究模型（1）的分岔周期解。

1 Hopf分岔的存在性

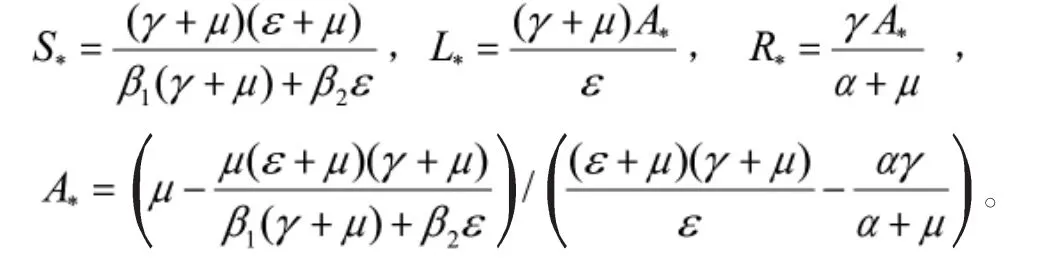
引理1[9]如果，则当∈[0，0)时，系统（1）局部渐近稳定。当=0时，系统（1）在 E(S*，L*，A*，R*)处产生 Hopf分岔，并且产生一簇分岔周期解。其中，

2 分岔周期解的稳定性

其中，

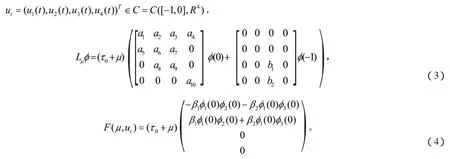
可以选取

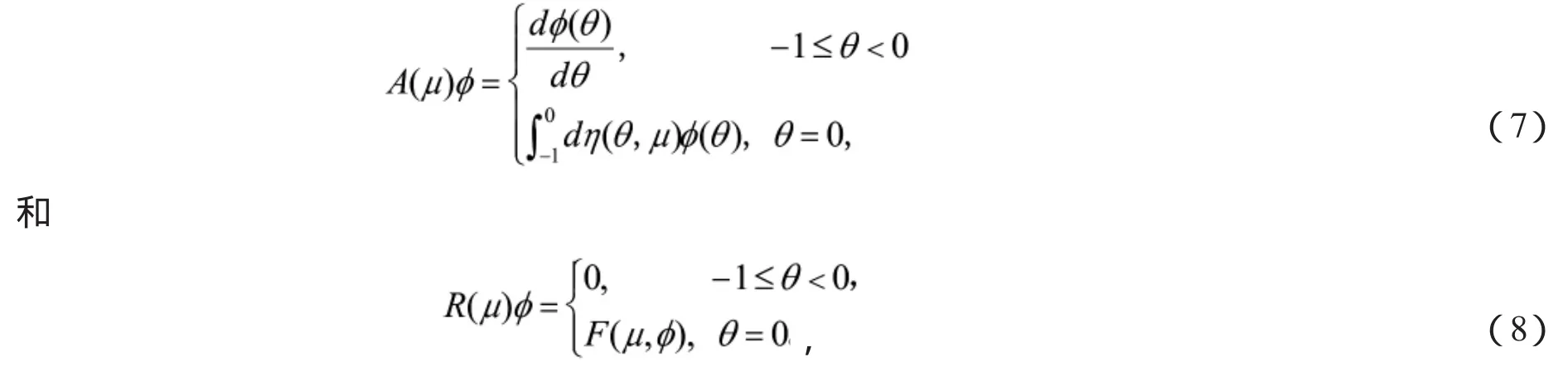
则系统（2）可以转化为

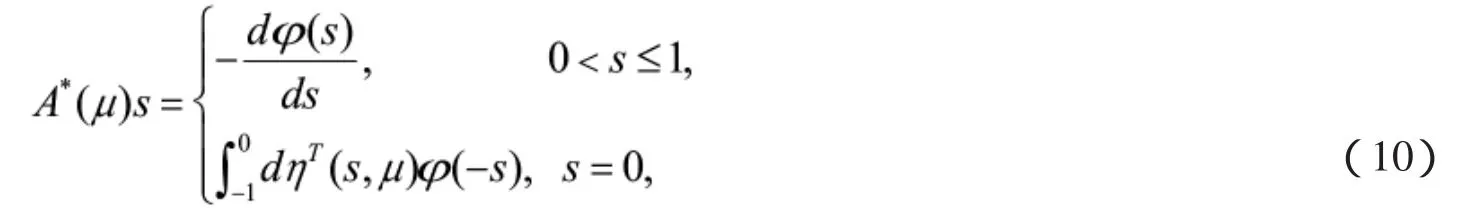
以及双线性内积

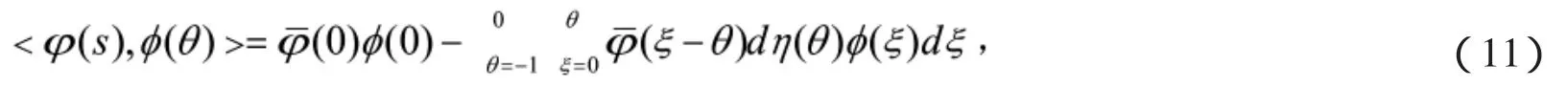
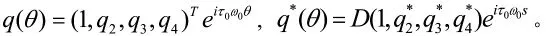
其中，

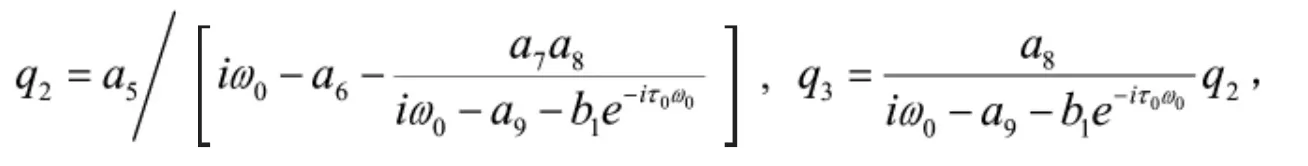
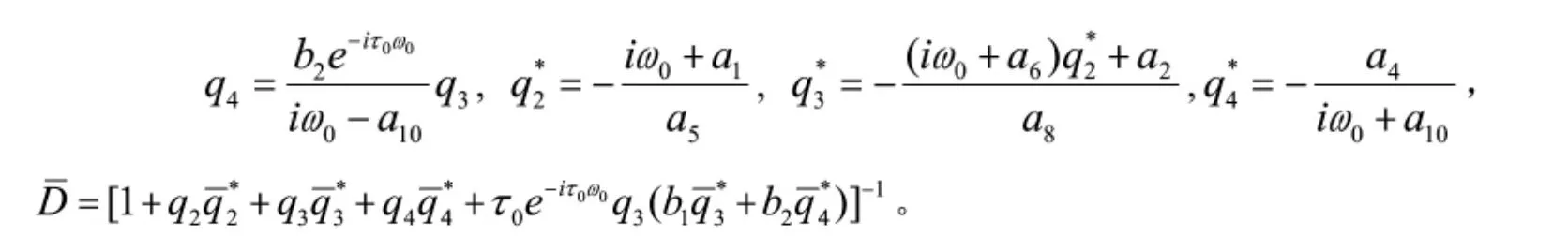
接下来，利用文献[14]中的算法以及计算过程，可以得到下列参数表达式：

E1和E2可以根据下列方程得到

最后，可以计算得到下列参数的表达式：

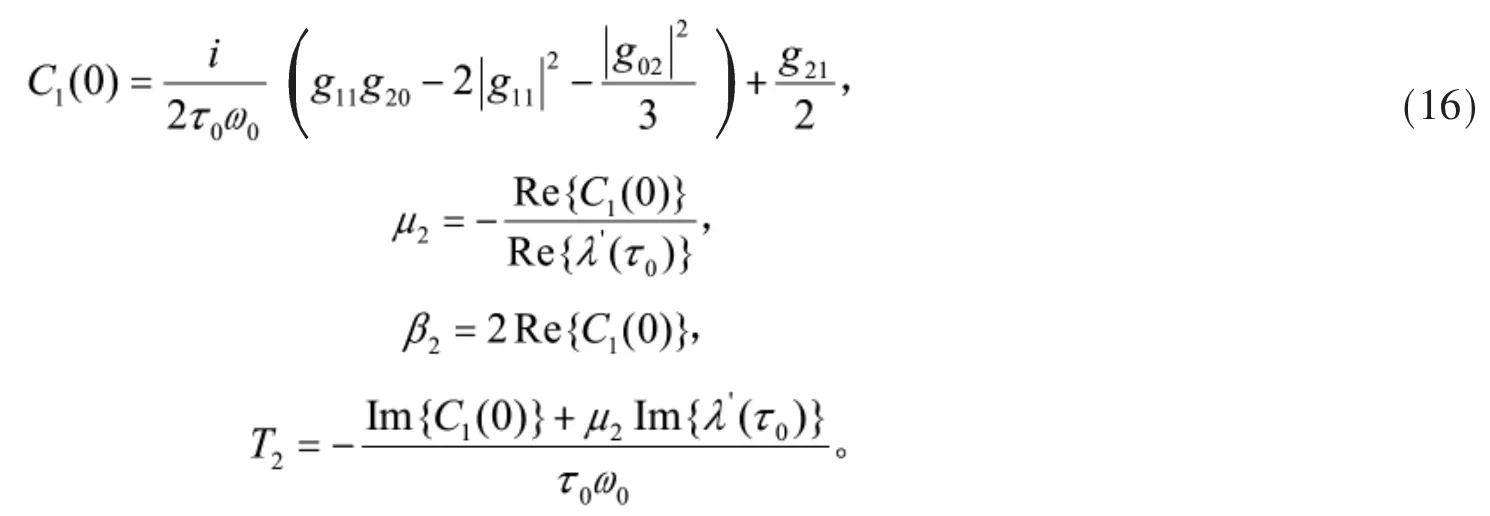
由上，可以得到如下关于分岔周期解的结论。

定理1 对于模型（1），当 μ2＞0(μ2＜0)，则 Hopf分岔是超临界(次临界)的；当 β2＜0(β2＞0)，则分岔周期解是稳定(不稳定)的；当 Τ2＞0(Τ2＜0)，则分岔周期解的周期是递增(递减)的。

3 仿真示例

直接计算得到，系统(17)的唯一有病毒平衡点 E(0.1116，0.2073，0.4936，0.1936)，进而得到。当时，如图1所示，系统（17）是局部渐近稳定的。当时，系统（17）则失去稳定性，产生Hopf分支并在平衡点附近产生一簇分支周期解。仿真效果如图2所示。另外，根据公式（16）计算得到，C1(0)=-21.6027+13.5870i，μ2=3.3172＞0，β2=-43.2054＜0，T2=-0.0427＜0。因此，根据定理1 可知，在附近产生的Hopf分岔是超临界的，分岔周期解是稳定的并且其周期是递增的。

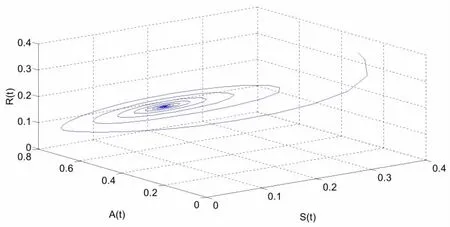
图1 当时，系统（17）渐近稳定

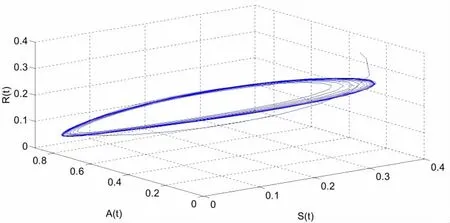
图2 当时，系统（17）不稳定并发生Hopf分支

4 结论

本文在文献[9]的基础上，进一步研究了一类时滞SLARS网络病毒传播模型的分岔周期解，所得理论结果是对文献[9]的适当补充。研究表明，当时滞t的取值足够小时，模型处于理想的渐进稳定状态，有利于网络病毒传播的控制。当时滞t的值越过临界值时，模型将失去稳定，产生分岔周期解。此时，网络病毒的传播将失去控制。仿真结果表明，当满足一定条件时，模型（1）中的四种状态的主机数量将以周期震荡形式共存。这种情况说明，模型中的时滞是有害时滞，应该尽量减小或者消除。在现实网络中，可以通过不断更新反病毒软件以达到减小模型中的时滞，保证模型处于渐近稳定状态。

[1]PIQUEIRA J R C，ARAUJO V O.A modified epidemiologicalmodel forcomputerviruses[J].Applied Mathematics and Computation，2009，213（2）：355-360.

[2]COHEN F.Computer virus：Theory and experiments[J].Computers&Security，1987，6（1）：22-35.

[3]彭梅，李传东，何兴.基于直接免疫的SEIR计算机病毒传播模型[J].重庆师范大学学报，2013，30（1）：77-80.

[4]PENG M，HE X，HUANG J J，et al.Modeling computer virus and its dynamics[J].Mathematical Problems in Engineering，Article ID 842614，2013：1-5.

[5]MISHRA B K，SAINI D K.SEIRS epidemic model with delay for transmission of malicious objects in computer network[J].Applied Mathematics and Computation，2007，188（2）：1476-1482.

[6]WANG C L，CHAI S X.Hopf bifurcation of an SEIRS epidemic model with delays and vertical transmission in network[J].Advances in Difference Equations，2016，2016（1）：1-19.

[7]WANG F W，YANG F，ZHANG Y K.et al.Stability analysis of a SEIQRS model with graded infection rates for Internet worms[J].Journal of Computers，2014，9（10）：2420-2427.

[8]BADSHAH Q.Global stability of SEIQRS computer virus propagation model with non-linear incidence function[J].Applied Mathematics，2015，6（1）：1926-1938.

[9]张子振，尹发，缑超博.一类具有分级感染率的时滞网络病毒传播模型稳定性[J].蚌埠学院学报，2016，5（2）:19-22.

[10]野金花，朱焕.一类具有阶段结构和Holling III类功能反应的捕食系统的一致持久性[J].黑龙江八一农垦大学学报，2017，29（1）：144-146.

[11]宋利民，张子振.具有隔离策略的网络病毒传播模型周期解[J].菏泽学院学报，2016，38（5）：56-62.

[13]刘昌东，江如，柴华金.一类具群体防御状态及Holling III型功能反应的捕食系统正周期解的全局吸引性[J].广东海洋大学学报，2016，36（3）：89-97.

[14]HASSARD B D，KAZARINOFF N D，WAN Y H.Theory and applications of hopf bifurcation[M].Cambridge University Press，Cambridg e，1981.

Periodic Solutions to a Delayed SLARS Computer Virus Propagation Model

ZHAO Tɑo，WEI Sulin，QI Zijiɑn，ZHANG Zizhen
（School of Management Science and Engineering，Anhui University of Finance and Economics，Bengbu Anhui 233030，China）

A series of delayed SLARS computer virus propagation model with graded infection rate was studied in this paper.Taking the delay of the model as bifurcation parameter，the critical point of time delay for Hopf bifurcation has been determined.Meanwhile，based on the central manifold theorem and the canonical form theory，the properties of the Hopf bifurcation at the critical point of the delay has been determined in this paper.

SLARS Model；Delay；Hopf Bifurcation；Periodic Solution

O175.12

A

1009-8666（2017）08-0025-06

［责任编辑、校对：李书华］

10.16069/j.cnki.51-1610/g4.2017.08.006

2017-04-02

2014年度安徽省高等学校自然科学项目“基于网络断层扫描的Ad Hoc网络测量技术研究”（KJ2014A006）；2016年度安徽省自然科学研究项目“基于网络层析成像的Ad Hoc网络测量模型与方法研究”（1608085QF145）

赵涛（1981—），男，安徽蚌埠人。安徽财经大学副教授，博士，研究方向：网络安全；魏苏林（1971—），男，安徽蚌埠人。安徽财经大学讲师，硕士，研究方向：网络安全。