有向通弦二部图的最小秩问题研究

牟谷芳

（乐山师范学院 数学与信息科学学院，四川 乐山 614000）

有向通弦二部图的最小秩问题研究

牟谷芳

（乐山师范学院 数学与信息科学学院，四川 乐山 614000）

有向二部图的最小秩问题等价于研究与之对应的符号模式矩阵的最小秩问题。文章研究了具有特殊结构的有向通弦二部图的最小秩问题，而获得了有向通弦二部图的最小秩为其团覆盖数，并将有向二部图的最小秩问题用于职场的双选会中。

有向通弦二部图；符号模式矩阵；最小秩

0 引言

无向图和有向图广泛用于特殊矩阵的最小秩计算中。图的最小秩问题最早是由P.M.Nylen[1]提出来的，他将实对称矩阵与无向树结合起来研究了实对称矩阵的最小秩问题，并给出了求解方法的有效算法。由此，树的最小秩问题就产生了。之后，S.M.Fallat和L.Hogben等人将无向树的最小秩问题推广到了一般无向图的最小秩问题[2]。利用无向图计算所有实对称矩阵所对应的对称零-非零模式矩阵的最小秩。由此，将无向图的最小秩问题自然推广到了有向图的最小秩问题，利用有向图来研究实非对称矩阵所对应的非对称零-非零模式矩阵的最小秩问题。由于利用代数方法计算特殊矩阵的最小秩较为困难，于是，通过图的一些图参数（路覆盖数 P(G)[2]，团覆盖数 CC(G)[2]，零迫集Z(G)[3]，图的最小度数[4]，图的最大匹配数match(G)[5]等）来确定图的最小秩的下界或上界。在文献[6]中，研究了无向通弦二部图的最小秩问题，且获得了无向通弦二部图的最小秩为其团覆盖数。在此基础上，本文研究了特殊有向通弦二部图的最小秩问题，且获得了有向通弦二部图的最小秩为其团覆盖数，并将有向二部图的最小秩问题应用于职场的“双选”中。

1 预备知识

下面介绍符号模式矩阵和有向通弦二部图的一些重要定义。

定义1.1[7]设A=(aij)是一个n阶实矩阵，以aij的符号{+，-，0}为元素所组成的矩阵称为A的符号模式矩阵(Sign Pattern)，记为P。由与A有相同符号模式的所有实矩阵所组成的集合称为由A所决定的定性矩阵类 (Qualitative Matrix Class)，记为。

定义1.2[8]设P是一个n阶符号模式矩阵，P的最小秩定义为：

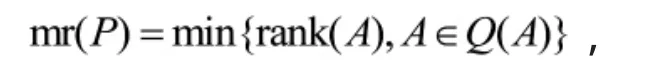
其中min表示最小值。

定义1.3[9]一个图G由两部分组成有限的非空顶点集V和边集E。图G的阶数是G的顶点个数，记为|G|。一个若无重边和环的图称为简单图。

定义1.4[9]一个有向图是由非空有限集合V与集合E构成，记为Γ，其中V中元素为顶点，E中元素为不同顶点的有序对，称为弧或有向边。

定义1.5[9]在一个有向图中，有向边集{{i1，i2}，…{ik-1，ik}}的各个顶点都不同，称从点i1到点ik的一条路（path），k为路的长度。若i1与 ik重合则称{{i1，i2}，…{ik-1，ik}}为一个回路。

定义1.6[9]若图G的顶点集V能够被分为两个子集U，V（称为部集），使得 G的每条边必然连接U中一个顶点和V中一个顶点（记G得边集为E(G)），称G为二部图，记为G(U，V)。然而，这并不意味着U中每个顶点与V中每个顶点邻接。

定义1.7[9]设M是E(G)的子集，如果M中任意两条边在G中均不邻接，则称M是G(U，V)的一个匹配，并记M所含的边数为|M|。

定义 1.8[10]设 G(U，V)为二部图，P为一符号模式矩阵，其中，U={1，2，…，n}（对应 P的行标集）和 V={1′，2′，…，n′}（对应P的列标集）。若图G中的每边都带有符号，则称G为符号图，记为 G＝（V，E，sign），且 G（U，V）每边的符号由P的符号来确定。若P中元素为正，则边{i，j′}标为“+”，i∈U，j′∈V；若P中元素为负，则边{i，j′}标为“-”，i∈U，j′∈V；若在 P中元素为零，在G(U，V)中不存在边。

定义 1.9[10]设 G(U，V)=(V，E，sign)为符号二部图。若边的符号为正，则有向边{i，j′}∈E，i∈U，j′∈V；若边的符号为负，则有向边{j′，i}∈E，i∈U，j′∈V，G(U，V)称为有向二部图。

由有向图的出度与入度的定义，我们给出了有向二部图的出度与入度的定义。

定义 1.10 在有向二部图 G(U，V)中(i∈U，j′∈V)，若（i，j′）∈E，为 G(U，V)的一条边，则称顶点j′是顶点i一个邻接点；若边{i，j′}的符号为正时，称j′是i的一个“出度点”；若边{i，j′}的符号为负时，j′是 i的一个“入度点”。顶点i的所有“出度点”的个数，称为i的出度(out degree)，记为 deg+(i)；顶点 i的所有“入度点“的个数，称为i的入度(in degree)，记为deg-(i)。

定义1.11[6]对于二部图G(U，V)（部集为 U={1，2，…，n}和 V={1′，2′，…，n′}），若 U中的每一个顶点都和V中的每个顶点连接，则称G(U，V)为完全二部图 (complete bipartite graph)。

定义1.12[6]若二部图中不含有长度为6或大于6的回路，称为通弦(chordal bipartite)二部图。

定义1.13[6]若二部图能用r个完全二部子图将G(U，V)的所有边全部覆盖，且 r最小，则称 r为其团覆盖数，记为bi(G(U，V))，其中，G(U，V)的团是其一个完全二部子图。

根据定义1.12和定义1.13，给出有向完全二部图和有向通弦二部图的定义。

定义1.14对于有向二部图G(U，V)（部集为 U={1，2，…，n}和 V={1′，2′，…，n′}），若 U中的每一个顶点都和V中的每个顶点连接，且U中的每一个顶点为出度点（或V中的每一个顶点为出度点），则称G(U，V)为有向完全二部图(directed complete bipartite graph)，若｜U｜=s，｜V｜=t有向完全二部图可记为 Ks，t。

定义1.15 若有向二部图中不含有长度为6或大于6的有向回路，称为有向通弦(directed chordal bipartite)二部图。

引理1.16[6]对任意带有完美匹配M的通弦二部图 G(U，V)，它的团覆盖数 bi(G(U，V))=｜M｜。

引理1.17[6]设G(U，V)是一个无向二部图，则它的最小秩 mr(G(U，V))≤bi(G(U，V))。

引理1.18[6]设G(U，V)是一个无向通弦二部图，则它的最小秩

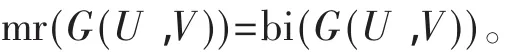
2 有向通弦二部图的最小秩

对于一般有向图的最小秩问题目前还没有很好的解决方法。近些年来，在符号图的最小秩研究问题中，主要是研究特殊图的最小秩计算方法和最小秩的上下界。本文在无向通弦二部图的最小秩问题的研究基础上，研究了有向通弦二部图的最小秩问题，并将有向二部图的最小秩应用于实际问题中。

引理2.1 若有向二部图G(U，V)为 n-有向回路，则 mr(G(U，V))=n-1。

证明：设 G(U，V)为 n-有向回路，它所对应的符号模式矩阵为

在P的行列展开式中有两非零项，且符号不同，则mr(P)≠n，同时 P中含有一个 n-1阶的下三角矩阵，则mr(P)=n-1，故有向二部图G(U，V)的最小秩 mr(G(U，V))=n-1。

特别地，当k≤4时，G(U，V)为有向通弦二部图，且它的最小秩为1。

引理 2.2 若有向二部图 G(U，V)为 n阶完全有向二部图，则mr(G(U，V))=1。

证明：根据定义 1.14知，n阶完全有向二部图G(U，V)所对应的符号模式矩阵各元素的符号都相同，则mr(G(U，V))=1。

定理2.3 设G(U，V)是一个有向二部图，则它的最小秩 mr(G(U，V))≤bi(G(U，V))。

证明：设 G(U，V)中的团覆盖数为 r，构建每一个团所对应的符号模式矩阵Pi(i=1，2，..，r)，且每个矩阵的最小秩为1。再将这些矩阵相加得到一个新矩阵P，它所对的二部图为G(U，V)，显然 mr(P)≤r。故 G(U，V)的最小秩 mr(G(U，V))≤bi(G(U，V))。

定理2.4 设G(U，V)是一个有向二部团块图，且每个团图为k-有向回路（k≤4）或为完全有向二部图，则它的最小秩mr(G(U，V))=bi(G(U，V))。

证明：根据引理2.1和引理2.2知，mr(G(U，V))≥bi(G(U，V))再由定理2.3 可得 mr(G(U，V))=bi(G(U，V))。

定理2.5 在一个有向通弦二部图G(U，V)中，若 G(U′，V′)是 G(U，V)中带有唯一完美匹配M′的最大子图，则

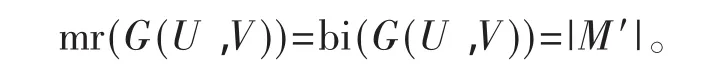
证明：若 G(U′，V′)=G(U，V)，结论显然成立。

若 G(U′，V′)≠G(U，V)，首先寻找 G(U，V)中的通弦二部子图K2.2，设团数为r。然后删除这些团，得二部图为G(U″，V″)。利用文献[10]算法3.1寻找带有唯一完美匹配M″的最大子图，则｜M′｜=｜M″｜+r。

根据引理2.2和定理2.4，结论成立。

3 应用

图的最小秩问题广泛应用于通信网络和信息科学中[11-12]，尤其在通信复杂度上有重要应用，如在文献[11]中，利用符号模式的最小秩确定了通信复杂度的一个下界。本节将通弦二部图的最小秩问题应用于职场招聘会的双选中。

例3.1 设有5位大学毕业生：A1，A2，A3，A4，A5，某企业公开招聘的岗位有顾问，编辑，程序员，秘书，培训师五个岗位。为了方便后面的叙述，将毕业生与不同岗位进行编号：A1，A2，A3，A4，A5，分别对应 1，2，3，4，5；顾问，编辑，程序员，秘书，培训师分别对应 1′，2′，3′，4′，5′。在职场招聘会上，不同的毕业生和各个岗位对应的情况如下：

1∶2′，3′；2∶1′，2′，4′，5′；3∶2′，3′；4∶2′，3′；5∶4′，5′。

假设每个岗位只招一人，试问每个毕业生是否能够挑选到合适的工作？

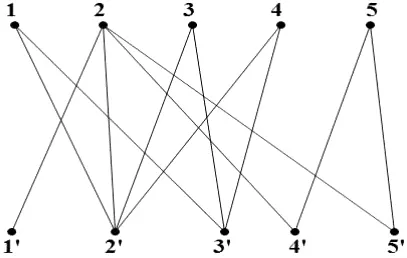
图1 二部图G(U，V)

图2 G(U，V)的完美匹配

方案：毕业生与岗位对应的情况利用二部图G(U，V)（如图1所示）来建立模型，其中U={1，2，3，4，5}，V={1′，2′，3′，4′，5′}。容易判断G(U，V)是无向通弦二部图，且团覆盖数为3。由引理2.2知，G(U，V)的最小秩为3。因此，至少有3位毕业生能找到合适工作。但是图1中的完美匹配不是唯一的，故不是每个人都能够找到合适的工作。

根据文献[10]算法3.1，在图3中能够找到一个最大唯一完美匹配（如图2所示）：

M′∶{{1，2′}，{2，1′}，{3，3′}，{5，5′}}。

因此，A1，A2，A3，A5 能找到合适的岗位，且分别对应的岗位为编辑，顾问，程序员，培训师。

在工作岗位招聘过程中，不仅毕业生想要挑选一份满意的工作，而且工作岗位对毕业生也有不同的要求，比如英语水平、计算机等级水平和专业技术水平等因素，工作岗位也要挑合适的人选，即为校园招聘“双选会”。因此，我们将有向通弦二部图的最小秩问题应用于职场“双选会”的研究中。

例3.2 设有4位大学毕业生：A1，A2，A3，A4，某企业公开招聘的岗位有编辑，程序员，秘书，培训师4个岗位。将毕业生与不同岗位进行编号：A1，A2，A3，A4，分别对应1，2，3，4；编辑，程序员，秘书，培训师分别对应 1′，2′，3′，4′。在职场招聘会上，不同的毕业生挑选不同岗位的情况如下：

1∶1′，2′，3′，4′；2∶1′，3′；3∶1′，2′；4∶1′，4′。

反之，不同的工作岗位挑选不同人选的情况如下：

2′∶2，4；3′∶3，4；4′∶2，3。

假设每个岗位只招一人，试问每个毕业生是否能够挑选到合适的工作？ 反之，工作岗位能否招到合适的人员？

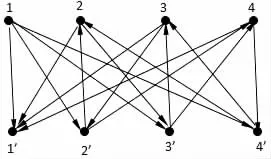
图3 有向二部图G(U，V)

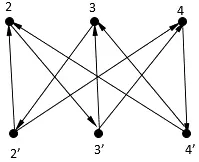
图4 有向二部子图G(U1，V1)

方案：毕业生与岗位对应的情况利用有向二部图G(U，V)（如图3所示）来建立模型，其中 U={1，2，3，4，}，V={1′，2′，3′，4′}。与 G(U，V)所对应的符号模式矩阵为

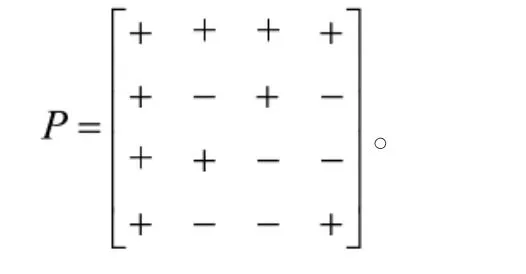
将P用于职场“双选会”的研究中，可以从如下两个方面来考虑。

一方面考虑每个毕业生能否挑选到自己满意的工作。

根据毕业生挑选的岗位情况 1∶1′，2′，3′，4′；2∶1′，3′；3∶1′，2′；4∶1′，4′可知，在有向二部图G(U，V)中不能够找到一个最大唯一完美匹配。因此，不是每个人能够找到合适的工作。若在G(U，V)的U和 V中分别删除顶点1和 1′，得到子图G(U1，V1)（见图4）。在G(U1，V1)中能够找到一个最大唯一完美匹配（如图5所示）：

M′＝{{2，3′}，{3，2′}，{4，4′}}。

因此，A2，A3，A4能找到合适的岗位，且分别对应的岗位为秘书，程序员，培训师。

图5 最大完美匹配

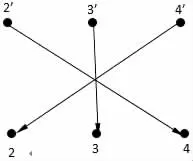
图6 最大完美匹配

另一方面考虑每个工作岗位能否挑选到合适的人选。

根据毕业生挑选的岗位情况 2′∶2，4；3′∶3，4；4′∶2，3 可知，在有向二部图 G(U1，V1)中能够找到一个最大唯一完美匹配（如图6所示）：

M″∶{{2′，4}，{3′，3}，{4′，2}}。

因此，培训师，秘书，程序员能找到合适的人选，且分别对应的人选为A2，A3，A4。

容易判断G(U，V)是有向通弦二部图，且团覆盖数为3。由定理2.4知，G(U，V)的最小秩为3。因此，有3位毕业生能找到合适工作和3个岗位能够找到合适的人员。

（本文部分内容系笔者2015年电子科技大学博士毕业论文《矩阵完备化和图的最小秩问题》）

[1]NYLEN P M.Minimum-rank matrices with prescribed graph[J].Linear Algebra Appl.，1996，248：303-316.

[2]FALLAT S M，统 HOGBEN L.Theminimum rank of symmetric matrices described by a graph：a survey[J].Linear Algebra Appl.，2007，426:558-582.

[3]HOGBEN L.Minimum rank problems[J].Linear Algebra Appl.，2010，432:1961-1974.

[4]AIM Minimum Rank-Special Graphs Work Graph.Zero forcing sets and theminimum rank of graphs[J].Linear Algebra Appl.，2008，428：1628-1648.

[5]IMA-ISU Research Group.Minimum rank of skew-symmetric matrices described by a graph[J].Linear Algebra Appl.，2009，432：2457-2472.

[6]JOHNSON C R，MILLER J.Rank decomposition under combinatorial constraints[J].Linear Algebra&Its Applications，1997，251：97-104.

[7]DEALBA L M，HARDY T L，HENTZEL I R，et al.Minimum rank and maximum eigenvalue multiplicity of symmetric tree sign patterns[J].Linear Algebra Appl.，2006，418：389-415.

[8]LI Z S，GAO Y B，ARAV M，et al.Sign patterns withminimum rank two and upper boundsonminimum ranks[J].Linear Multilinear A.，2014，61：895-908.

[9]张先迪，李正良.图论及其应用[M].北京：高等教育出版社，2005：2.

[10]牟谷芳，黄廷祝.符号有向图的最大SNS-符号模式矩阵[J].工程数学学报，2015（5）：772-782.

[11]BURGARTH D，ALESSANDRO D D，HOGBEN L.Zero forcing，linear and quantum controllability for systems evolving on networks[J].Automatic Control，IEEE Transactions on，2013，58:773-784.

[12]LINIAL N，MENDELSON S，SCHECHTMAN G，et al.Complexity measures of sign matrices[J].Combinatorica，2007，27：439-463.

The Minimum Rank Problem Research of Directed Chordal Bipartite Graph

MU Gufɑnɡ
（School of Mathematics and Information Science,Leshan Normal University,Leshan Sichuan 614000,China）

Theminimum rank problem of directed bipartite graph is equivalent to the correspondingminimum rank problem of symbolic pattern matrix.In this paper，theminimum rank problem of directed chordal bipartite graph with a special structure has been studied.In this case,theminimum rank of a directed chordal bipartite graph is its clique coverage number.Beside，theminimum rank problem of directed chordal bipartite graph is used in job fair based on mutual selection.

Directed Chordal Bipartite Graph；Symbolic Pattern Matrix；Minimal Rank

O157.6

A

1009-8666（2017）08-0005-06

［责任编辑、校对：李书华］

10.16069/j.cnki.51-1610/g4.2017.08.002

2017-04-13

四川省教育厅资助科研项目“有向图的最小秩问题及其在通信网络中的应用”（17ZB0193）；乐山师范学院资助科研项目“有向图的最小秩问题及其应用”（Z1521)

牟谷芳（1981—），女，土家族，湖北恩施人。乐山师范学院数学与信息科学学院讲师，博士，研究方向：组合矩阵论。