水质检测化验误差数据处理与分析

李伟晶

(辽宁省锦州水文局，辽宁 锦州 121000)

水质检测化验误差数据处理与分析

李伟晶

(辽宁省锦州水文局，辽宁 锦州 121000)

水质监测与检测是区域水资源保护工作中的重要一环。文章主要以辽宁省锦州市为例，对该研究区水质检测化验误差数据处理与分析相关内容展开论述。文中首先针对水质检测误差分析中常用的两大概念"真值与平均值"进行介绍，在此基础上，分别对误差与误差类型、准确度与精密度等相关内容进行简介，从而为本研究水质检测化验误差数据处理、分析提供理论依据。

水质检测；化验；误差；数据处理

0 前 言

水质检测可保证水资源质量安全、可靠，它是保证农村地区饮用水健康的重要方式。但在水质检测过程中，受主、客观因素影响和制约，如农村地区检测设备、技术方式等相对落后等，这些因素会在一定程度上严重干扰水质测定结果；再加上水质检测过程中技术人员主观失误和责任意识不强，经常会导致水质检测化验数据出现误差。所以，对水质检测化验误差数据进行处理、分析尤为重要。通过水质检测化验数据误差处理与分析，即可找到影响水质检测结果的主要因素，以便控制干扰因子，消除不良影响，保证水质检测结果准确、客观与完整。

1 水质检测化验误差数据处理与分析技术依据

1.1 水质检测化验误差数据处理与分析中的真值与平均值

水质检测化验误差数据处理与分析主要是以检测数据误差及其在运行中产生的相关影响为对象，确定水质最终检测结果的精确性。从本质上而言，水质检测化验数据误差是客观存在的，只要保证误差控制在合理范围内，都是可行的。但误差过大就会影响水质测定结果，不利于对研究区水质总体情况作出客观判断与分析[1]。而水质检测数值是物理量的真实值，在水质检测中一般无法得到真值，只能通过平均值代替水质检测化验真值；同时，水质测定次数有限，只能通过多次测定中取得的平均值作为近似测定结果，对水质状况进行合理判断。在水质测定中，常用的平均值主要分为算术平均值、均方根平均值、加权平均值、中位值、几何平均值几种。具体测定化验误差数据处理计算公式分别如下：

1)锦州市水质检测化验误差数据处理与分析中的算术平均值计算：

公式如下：

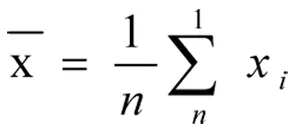
(1)

2)锦州市水质检测化验误差数据处理与分析中的均方根平均值误差计算：

公式如下：

(2)

3)锦州市水质检测化验误差数据处理与分析中真值计算：

公式如下：

A=x±△x

(3)

4)锦州市水质检测化验误差异常数据处理与取舍：

公式如下：

(4)

5)锦州市水质检测化验误差数据处理与分析中合理判断K值：

公式如下：

(5)

2.2 水质检测化验误差数据处理与分析中的常见误差与类型

水质检测化验中的误差分为绝对和相对误差2种。其中，绝对误差是指水质检测值与真实值之间的差值。因水质检测真实值难以获得。因此，在实践中经常采用检测值与平均值之间的差表示水质检测绝对误差。

在检测过程中，只需将标准式样中某成分实际含量作为该组分的真值，即可以此为标准对检测误差进行估算。对误差分析准确度进行判断时，经常采用相对误差这一指标来衡量[2]。

其中，绝对误差/平均值=相对误差。

在对水质检测化验过程中产生的相关数据误差进行分类，其中根据不同误差产生成因，可将误差分为不同种类，具体而言分为3种，分别是系统误差、随机误差与过失误差。这3种误差主要是由测定中不确定性因素和技术操作人员操作不规范所导致。

2.3 水质检测化验误差数据处理与分析中的准确度与精密度

对水质检测化验数据准确性进行分析，经常采用准确度与精确度两大指标来衡量。其中，准确度是指水质测定值与真实值之间的偏差，其可反映系统误差大小，通过相对误差来表示。而水质检测精密度主要是指在控制条件下，采用一个均匀试验进行反复测定，以此得到重复数据即可随机反映水质测定结果的准确性。这一指标可反映水质测定值与算术平均值之间的偏差程度。精密度是保证准确度的前提和基础，只有消除了水质测定误差，才能通过精密度表示水质测定准确度。而在水质测定结果分析中，先要通过对数据精密度进行考察，然后才能对其准确度进行分析，充分弄清二者关系有助于正确处理水质检测化验误差数据[3]。

3 水质检测化验误差数据处理与分析实践应用

3.1 直接法

直接数据处理是指直接从仪表中读取数据；而间接处理是指通过计算得到数据结果的方式。

1)水质检测化验误差数据处理与分析中的单项测量值误差。

在水污染环境检测过程中，经常会受相关技术条件和设备因素制约。因此，难以对数据进行准确测量，只有经过多次循环，才能得到具体数值。这些数值往往是平均近似值，需结合实际对其进行修正。在处理中，对于误差较小的结果只需结合仪表中的数据对其适当计算即可；而误差较大的数据需按仪器上最小刻度的1/2作为单项测量最大绝对误差。

2)水质检测化验误差数据处理与分析中多次重复测量值误差。

在水质测定结果分析中，为了得到准确数值，往往需经过多次重复测量与计算，用这些测量值的算术平均值即可近似度代替水质测量值的真值。其中，水质测量值的真值可表示为：

A=x±△x

(6)

(7)

另外，测量值与算术平均值的差-偏差即可表示为：

dxi=xi-x

(8)

算术平均误差即可表示为：

(9)

例如：在对锦州市2016年某研究区水质进行检测过程中，通过10次循环测定，最终得到如下10组原水浊度测定结果，分别为0.490、0.471、0.475、0.492、0.473、0.480、0.468、0.492、0.476、0.451，

按照上述计算公式，即可得到：

锦州市水质浊度算术平均值为：

(10)

锦州市水质浊度算术平均误差:

(11)

锦州市水质浊度真值为：

A=x±△x=锦州市水质浊度算术平均值±锦州市水质浊度算术平均误差=0.4902±0.00083

(12)

即可确定锦州市水质浊度测定真值处于0.4902-0.00083这一区间内。

3.2 间接法

与直接法不同，水质检测数据间接测量值主要是指将直接测量值代入不同计算处理公式得到的一种误差分析法。间接测量值的准确性受直接测量结果与公式形式等因素影响。间接测量误差主要是考察同一水质在不同误差情况下相加得到的误差情况。各项直接测量值绝对误差之和=只含和、差运算间接测量值的绝对误差；间接测量、直接测量值之间的函数关系含乘、除、乘方、开方等运算时，各直接测值相对误差之和=相对误差。当间接测量值计算公式只含加减运算时或含有乘、除、乘方、开方时，要分别先计算绝对误差，再计算相对误差或先计算相对误差，后计算绝对误差。

例如，在锦州市水质检测化验处理中，溶质直接测定量和使用分析天平测量的绝对误差WB分别为0.3468g和0.0003g。溶剂水质量W A在台秤上称刻度为26g，绝对误差=0.2g。置于60mL容量瓶中，容量瓶刻度绝对误差、溶质与溶剂水观测体积刻度分别为±0.06mL和V=26mL。则通过计算可得：

1)水溶质称量相对误差：

=ΔWB /WB=±0.0003/0.3468 =±1.5×10-3

2)水溶剂称量的相对误差：

=ΔWA /W A =±0.2/26 =±3×10-3

3)观测体积相对误差：

=ΔV/V =±0.06/26 =±3×10-3

由此可求得所配试剂的相对误差

=ΔWB /WB+ΔWA /WA+ΔV/V

=(±1.5×10-3)+(±3×10-3)+(±3×10-3)

3.3 水质检测化验误差数据处理与分析中的异常数据取舍

在水质检测化验数据处理分析中，经常需对异常数据进行取舍处理。通常采用的异常数据取舍方法有肖维涅准则。

例如：在锦州市水质检测化验处理中得到的一组PH实测数按照从大到小顺序排列，分别为9.62、9.24、8.98、8.92、8.81、8.79、8.71、8.67、8.61、8.56、8.48、8.39、8.37、8.31、8.17、7.19。其中数据9.62和7.19分别为最大值和最小值，与其它数据之间存在异常，所以按照以下计算公式即可对异常数据进行取舍：

根据公式：

(13)

在上述计算基础上，合理判断K值：

(14)

通过查表“n与K的对应值”当n为16时，k=2.26,

4 结 语

综上可知，文章重点对该研究区水质检测化验误差数据处理与分析方法进行阐述，文中提出了单项测量值的误差分析、多次重复测量值的误差分析、直接与间接测量值的误差分析、异常数据取舍等水质化验误差数据处理与分析方法。实践结果表明，直接计算法与间接计算法、基于肖维涅准则的异常数据取舍法，均可有效提高锦州市水质测定、化验误差数据处理精确性，大大提高数据分析科学性，从而为锦州市水质检测结果分析提供了重要参考依据，上述方法值得应用与推广。

[1]程曼曼.季节性肯达尔检验法在南湾水库水质趋势分析中的应用[J].河南水利与南水北调, 2012(16)：57-58.

[2]韩静.汾河水库水质趋势分析[J].山西水利科技, 2009(01)：92-93，96.

[3]胡国华, 唐忠旺,肖翔群.季节性Kendall检验及其在三门峡水库水质趋势分析中的应用[J].地理与地理信息科学, 2004(03):86-88.

[4]朱佳佳.九龙江流域水环境状况及治理对策初探[J].水利技术监督,2009(04):27-29.

1007-7596(2017)08-0056-03

2017-08-16

李伟晶(1964-)，男，辽宁锦州人，工程师，从事水质化验、监督执法等工作。

X832

：B