造纸废水处理过程微小故障检测方法研究
2017-09-15王龄松马璞璠叶凤英熊智新赵小燕刘鸿斌
王龄松 马璞璠 叶凤英 熊智新 赵小燕 刘鸿斌,2,*
(1.南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037;2.华南理工大学制浆造纸工程国家重点实验室,广东广州,510640)
·废水处理过程检测·
造纸废水处理过程微小故障检测方法研究
王龄松1马璞璠1叶凤英1熊智新1赵小燕1刘鸿斌1,2,*
(1.南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037;2.华南理工大学制浆造纸工程国家重点实验室,广东广州,510640)
微小故障的检测是过程监测领域的一个重要研究方向。传统的多元统计过程监测方法无法对过程微小故障进行有效监控。本课题将多元累积和控制(CUSUM)方法及多元指数加权移动平均(EWMA)方法分别与主成分分析(PCA)相结合用于造纸废水处理过程中微小故障的过程监测。研究结果证实了多元累积和控制方法和多元指数加权移动平均方法的有效性。
造纸废水处理过程;主成分分析;累积和控制;指数加权移动平均;故障检测
(*E-mail: hbinjm@163.com)
随着科技的发展,现代控制系统和设备的复杂性不断增加、规模不断扩大,生产过程中的控制系统一旦发生故障将会造成巨大损失。在过程监测领域,故障的定义是系统的某个或某些特征或者变量发生了超过允许范围的偏差[1]。过程监测和故障诊断技术可以提高系统的可靠性,降低事故的风险,对于工业生产过程的正常运行起到非常重要的作用[2]。
流程工业生产过程中的测量变量往往相互关联,传统的单变量统计过程控制技术无法满足工业上的监控要求。基于多元投影理论的多元统计过程监控技术逐渐受到学术界和工业界的广泛重视,并且在化工生产过程中得到了成功的应用[3-5]。化工生产过程都存在着缓慢变化,比如设备的老化、催化剂的性能变化以及化学药品浓度的变化等,这些缓慢变化的微小故障如果不能及时地检测出来,轻则会导致产品质量的下降,重则甚至可能导致生产事故的发生。
累积和控制(Cumulative sum,CUSUM)与指数加权移动平均(Exponent weighted moving average,EWMA)是两种经典的单变量统计过程控制方法,广泛应用于单变量过程系统中微小信号的故障检测[6]。然而,单变量CUSUM和EWMA并没有考虑生产过程中多种变量之间的相关性,对于复杂的工业生产过程来讲,仅使用单变量监控不仅操作麻烦,图形众多,而且会带来频繁的误报和漏报问题[7]。为此,Chen等人[8]提出将CUSUM、EWMA与主成分分析(Principal component analysis,PCA)相结合来对微小故障进行检测。
针对造纸废水处理系统的多变量特性,本课题首先将单变量CUSUM和单变量EWMA进行多变量扩展,形成多变量CUSUM(Multivariate CUSUM, MCUSUM)和多变量EWMA(Multivariate EWMA, MEWMA),然后将MCUSUM和MEWMA作为数据预处理方法,最后将MCUSUM和MEWMA与PCA方法分别结合,构成MCUSUM-PCA和MEWMA-PCA方法。对造纸废水处理过程控制系统加入偏移和漂移两类故障信号,采用统计指标对系统进行过程监测和故障诊断。
1 故障检测方法简介
1.1 多变量统计过程监测
对于一组正常工况的数据Xm×n(式中,m为样本个数;n为变量个数),先将原始数据矩阵进行标准化处理,即将矩阵各列转化为均值为0,方差为1的向量。然后运用PCA,将X分解成等式(1):
(1)
式中,T∈Rm×r、P∈Rn×r分别为主元得分矩阵和载荷矩阵;E∈Rm×n为预测残差矩阵;r为主元个数,其值可用交叉检验或观察累积方差贡献率来确定。
原始数据矩阵经过降维处理后,变量之间相关性得到消除。通过对主元得分矩阵和预测残差矩阵进行变换,构建出两个统计量T2和Q,以检测造纸废水处理过程的微小故障。
对于测试数据xk=[xk,1,xk,2,…,xk,n]T,按照公式(2)计算统计量T2:
(2)
式中,Λ=diag(λ1,λ2,…,λr),λ为X的协方差矩阵的特征值。T2的统计控制限CL服从F分布,由式(3)计算得到:
(3)
式中,Fr,m-r,α表示自由度为r和m-r的F分布的上侧α分位数。当统计量超出控制限的时候,视为过程失控,系统发出报警。
统计量Q,又称平方预测误差统计量,其计算如公式(4):
(4)
式中,I为对角线全为1的单位矩阵。
统计量Q的统计控制限CL按公式(5)计算:
(5)

1.2 多元累积和控制图(MCUSUM)
工业生产过程中的缓慢变化和微小变化,如催化剂的缓慢失效,生产设备的逐年老化,以及测量设备的失灵等,会对生产过程造成不容忽视的不良影响。这些细微的变化如果不能被及时发现和处理,很有可能会影响到生产的进行以及产品的质量,甚至出现不可挽回的安全事故。对于微小故障的监控,多元累积和控制图(CUSUM控制图)和指数加权移动平均控制图(EWMA控制图)是单变量统计过程监控领域中的有效方法。该类方法只能对单变量过程进行监控,应用范围受到限制,无法满足当代复杂大型生产设备以及生产过程的复杂性要求。本课题采用如下多元累积和控制图(MCUSUM)方法对造纸废水处理系统进行微小故障检测。通过对多元数据中各个变量在d个时刻内的数据进行加和,一方面,可以放大数据中的微小变化,提高后续PCA的过程监测能力;另一方面,也能够降低异常数据对过程监测统计量的影响,增强监测系统的鲁棒性。
假设从过程中采集到的数据为Xm×n,对该数据进行处理,定义t时刻的累积和变量值为:
(6)
式中,d表示各样本累计和的步数,即从当前时刻往前推d个时刻;xi表示第i个采样;m为总的样本个数。为保证数据时效性及减少实际应用中的计算量,不对由yt构成的数据集进行归一化处理,直接将t≤d时的数据舍弃,然后对其进行传统PCA过程监测分析,从而实现与PCA的结合。
1.3 多元指数加权移动平均控制图(MEWMA)
当故障的幅值小于其所能够检测到的临界故障幅值时,传统的PCA故障检测方法无法有效地检测出该故障,而指数加权移动平均控制图(EWMA控制图)则适用于缓慢漂移和微小故障的检测。将MEWMA与PCA相结合可以提高主元分析的故障检测性能[8]。
作为单变量EWMA的扩展,MEWMA定义见公式(7):
zk=ωxk+(1-ω)zk-1
(7)
式中,0<ω≤1且z0=0。
X∈Rm×n经过MEWMA处理后变为Z∈Rm×n,Z的协方差矩阵为SZ[ω/(2-ω)]S,S为X的协方差矩阵。对经过MEWMA预处理过的数据矩阵进行传统PCA过程监测分析,从而实现与PCA的结合。
统计量T2采用公式(8)来计算[8]:
(8)
统计量Q采用公式(9)来计算[8]:
(9)
2 造纸废水处理过程故障检测
2.1 造纸废水处理过程数据
本课题所用的数据取自于广东东莞的一家造纸厂好氧段废水的监测数据。该数据含有170组测量值,8个过程及水质变量,如图1所示。图1中左边纵坐标对应于进水化学需氧量(CODinf)、出水化学需氧量(CODeff)、进水悬浮固形物(SSinf)、出水悬浮固形物(SSeff)值;右边纵坐标表示流量Q(104m3/d)、pH值、温度T(℃)和溶解氧浓度DO(mg/L)[9]。

图1 造纸废水处理过程数据
2.2 故障数据的构造
从故障诊断的角度分析,故障可以归纳为三类:传感器故障、执行器故障以及过程参数故障[1]。本课题以传感器故障检测为例来验证所提出微小故障检测方法的有效性。常见的传感器故障类型有偏移故障、漂移故障、完全故障以及精度下降故障[10]。本课题对传感器变量CODinf和pH值分别构建数据故障。对传感器变量CODinf加入均值的20%数据故障,对传感器变量pH值加入0.05系数的漂移故障,得到偏移和漂移两种故障类型(表1,图2)。在MATLAB软件中对170个造纸废水样本数据进行分析处理,前100个样本作为训练集,后70个数据作为测试集,测试集中取一部分数据加入故障信息(本课题从第121个采样点开始加入故障信息)。

表1 偏移和漂移故障引入公式
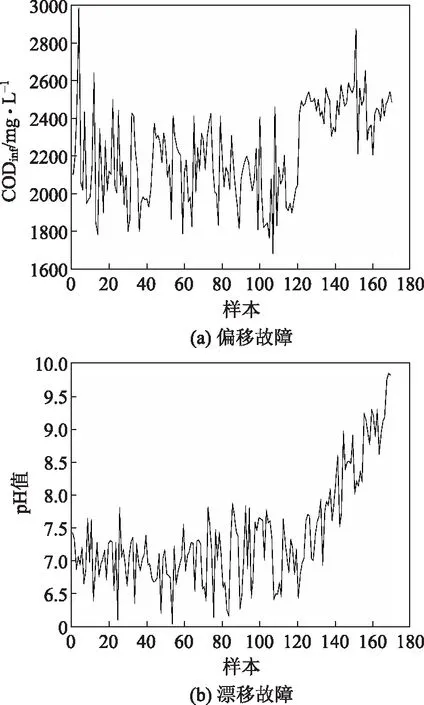
图2 偏移故障和漂移故障
2.3 MCUSUM和MEWMA中关键参数的确定
2.3.1 MCUSUM预处理中d值的确定
在MCUSUM算法中,参数d对故障检测结果有最直接的影响。通过对比偏移和漂移两组故障检测结果发现,MCUSUM-PCA的监控效果随着d值的增大而增强。较大的d值会使监控过程更加稳定,不会使控制图因为某一样本值的突变而发生剧烈变化。另一方面,d值的增大也意味着需要积累的数据量步数增大,故障检测的滞后也随之变大。综合考虑,本文d值选定为12。

图3 偏移故障的PCA检测结果

图4 偏移故障的MCUSUM-PCA检测结果(d=12)
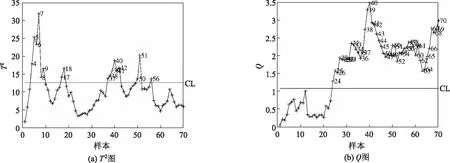
图5 偏移故障的MEWMA-PCA检测结果(ω=0.2)
2.3.2 MEWMA预处理中λ值的确定
在MEWMA算法中,权值参数ω对MEWMA-PCA统计量期望值的变化影响很大。当ω取较大值时(接近1),统计量能够及时地反映过程中的突然变化,从而对突变故障具有良好的检测性能,然而对于在检测过程中出现的缓变故障,却会出现漏报情况;而当ω取较小值时(接近0),MEWMA能够起到很好地平滑作用,能够过滤过程中的噪声,但同时也会引起一定的检测滞后。因此,ω参数的选取要综合考虑噪声和检测滞后两个方面,二者权衡,以求达到最好的检测效果。经过对造纸废水处理数据的多次模拟试验,最终确定ω=0.2。
2.4 故障检测结果与分析
2.4.1 偏移故障检测结果
使用PCA、MCUSUM-PCA和MEWMA-PCA分别对偏移故障数据进行检测,结果如图3~图5所示。对于偏移故障,计算结果表明,MCUSUM-PCA与MEWMA-PCA两种方法都能够在故障(21~70样本点)出现后的3~4个样本点内检测出故障,监测过程超过控制线而发出故障报警(图4和图5)。相比较而言,PCA方法对偏移故障的检测效果较差(图3)。

图6 漂移故障的PCA检测结果

图7 漂移故障的MCUSUM-PCA检测结果(d=12)
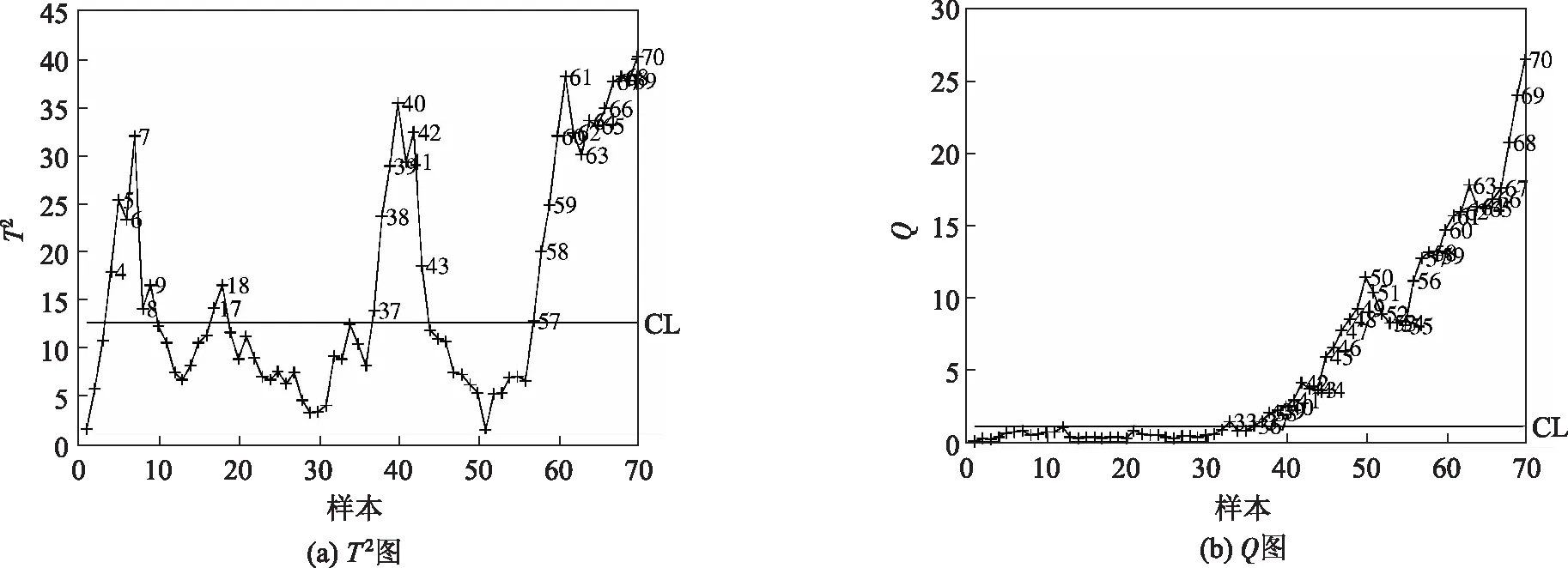
图8 漂移故障的MEWMA-PCA检测结果(ω=0.2)
PCA、MCUSUM-PCA和MEWMA-PCA的故障正确检测率如表2所示。MCUSUM-PCA和MEWMA-PCA的Q统计指标的正确检测率分别为0.96和0.94,MEWMA-PCA检测出的异常数据比MCUSUM-PCA滞后一个样本点。从图4和图5中可以看出,两种方法对出现故障之后的持续异常状态都取得了有效的监控。然而,PCA方法的Q统计指标的正确检测率只有0.16,这是因为偏移故障的幅度变化比较微小,常规的PCA监测方法无法对故障造成的微小变化进行积累,导致无法对故障进行准确的检测。
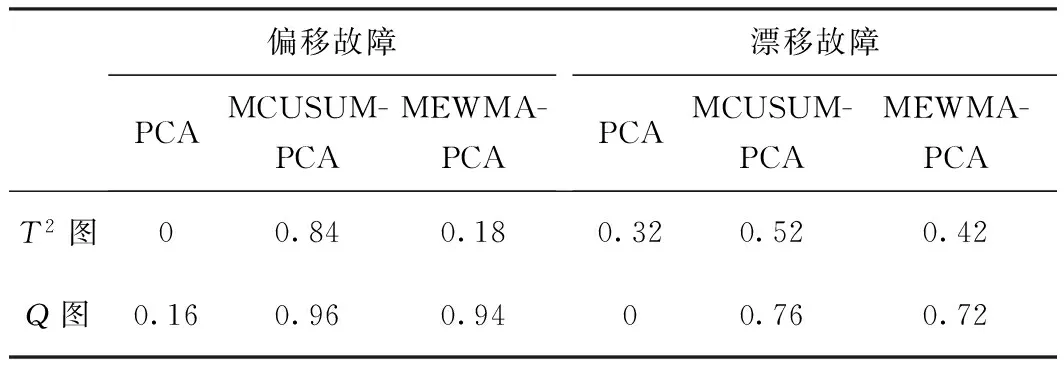
表2 PCA、MCUSUM-PCA和MEWMA-PCA对偏移故障
2.4.2 漂移故障检测结果
使用PCA、MCUSUM-PCA和MEWMA-PCA分别对漂移故障数据进行检测,结果如图6~图8所示。对于漂移故障,MCUSUM-PCA与MEWMA-PCA两种方法都能够在故障(21~70样本点)出现后的10~15个样本点内检测出故障,监测过程超过控制线而发出故障报警(图7和图8)。相比较而言,PCA方法对偏移故障的检测效果较差(图6)。
PCA、MCUSUM-PCA和MEWMA-PCA的故障正确检测率如表2所示。MCUSUM-PCA方法的Q统计指标的正确检测率为0.76,MEWMA-PCA方法的Q统计指标的正确检测率为0.72。两种方法对漂移故障的正确检测率均小于其对偏移故障的正确检测率,原因在于漂移故障是一个缓慢变化的微小故障,需要一定的时间才能表现出故障的存在,在故障发生的初始时刻,统计指标并没有超出控制限,监测系统无法检测到此时的故障,直到故障信号积累到了一定程度,监测系统才能监测到故障发出报警。之后,两种方法对出现故障之后的持续异常状态都取得了有效的监控。而PCA方法的Q统计指标的正确检测率为0,这是因为漂移故障在用PCA方法检测时,残差空间并不能有效地表达过程的变化趋势,Q统计指标全部位于统计限之下,故没有进行故障报警。而对于T2统计指标,PCA方法对漂移故障的正确检测率也低于MCUSUM-PCA和MEWMA-PCA的T2和Q统计指标。
3 结 论
本课题采用多变量累积和控制(MCUSUM)、多变量指数加权移动平均(MEWMA)分别与PAC结合构成的MCUSUM-PCA、MEWMA-PCA及PCA三种多元统计方法对造纸废水处理过程进行监测研究。对于偏移和漂移的微小故障,MCUSUM-PCA和MEWMA-PCA的故障正确检测率均高于传统PCA方法的故障正确检测率。在故障检测的灵敏度方面,MCUSUM-PCA和MEWMA-PCA的表现也优于传统PCA监测方法。MCUSUM-PCA和MEWMA-PCA都能在故障出现2~3个样本点内就可检测出偏移故障,在10~15个样本点内就可检测出漂移故障;而传统PCA方法却因对微小故障的检测效果不明显而出现大量的漏检现象。
[1] HUANG Dao-ping, QIU Yu, LIU Yi-qi, et al. Review of data-driven fault diagnosis and prognosis for wastewater treatment[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(3): 111. 黄道平, 邱 禹, 刘乙奇, 等. 面向污水处理的数据驱动故障诊断及预测方法综述[J]. 华南理工大学学报 (自然科学版), 2015, 43 (3): 111.
[2] ZHOU Dong-hua, HU Yan-yan. Fault diagnosis techniques for dynamic systems[J]. Acta Automatica Sinica, 2009, 35(6): 748. 周东华, 胡艳艳. 动态系统的故障诊断技术[J]. 自动化学报, 2009, 35(6): 748.
[3] Liu Tian-long, Shen Wen-hao. A review of applications of fault diagnostic expertsystem in wastewater treatment[J]. Paper Science & Technology, 2011, 30(2): 75. 刘天龙, 沈文浩. 污水处理过程中故障诊断专家系统的应用[J]. 造纸科学与技术, 2011, 30(2): 75.
[4] QIN S. Joe. Survey on data-driven industrial process monitoring and diagnosis[J]. Annual Reviews in Control, 2012, 36(2): 220.
[5] JI Hong-quan, HE Xiao, ZHOU Dong-hua. Fault detection techniques based on multivariates statistical analysis[J]. Journal of Shanghai Jiaotong University, 2015, 49 (6): 842. 纪洪泉, 何 潇, 周东华. 基于多元统计分析的故障检测方法[J]. 上海交通大学学报, 2015, 49 (6): 842.
[6] LI Juan, ZHOU Dong-hua, SI Xiao-sheng, et al. Review of incipient fault diagnosis methods[J]. Control Theory & Applications, 2012, 29(12): 1517. 李 娟, 周东华, 司小胜, 等. 微小故障诊断方法综述[J]. 控制理论与应用, 2012, 29(12): 1517.
[7] GE Zhi-qiang, YANG Chun-jie, SONG Zhi-huan. Research and application of small shifts detection method based on MEWMA-PCA[J]. Information and Control, 2007, 36(5): 650. 葛志强, 杨春节, 宋执环. 基于MEWMA-PCA的微小故障检测方法研究及其应用[J]. 信息与控制, 2007, 36(5): 650.
[8] CHEN Junghui, LIAO Chien-Mao, LIN Franz Ren Jen, et al. Principle component analysis based control charts with memory effect for process monitoring[J]. Industrial & Engineering Chemistry Research, 2001, 40(6): 1516.
[9] YANG Hao, MO Wei-lin, XIONG Zhi-xin, et al. Soft Sensor Modeling of Papermaking Effluent Treatment Processes Using RPLS[J]. China Pulp & Paper, 2016, 35(10): 31. 杨 浩, 莫卫林, 熊智新, 等. 基于RPLS的造纸废水处理过程软测量建模[J]. 中国造纸, 2016, 35(10): 31.

(责任编辑:马 忻)
Incipient Fault Detection in Papermaking Wastewater Treatment Processes
WANG Ling-song1MA Pu-fan1YE Feng-ying1XIONG Zhi-xin1ZHAO Xiao-yan1LIU Hong-bin1,2,*
(1.JiangsuProvincialKeyLabofPulpandPaperScienceandTechnology,NanjingForestryUniversity,Nanjing,JiangsuProvince, 210037; 2.StateKeyLabofPulpandPaperEngineering,SouthChinaUniversityofTechnology,Guangzhou,GuangdongProvince, 510640)
Incipient fault detection has been an important research topic in the field of process monitoring. However, traditional multivariate statistical process monitoring methods fail to detect incipient faults. In this paper, two methods were developed for the incipient fault detection of a papermaking wastewater treatment process: multivariate cumulative sum combined with principal component analysis (PCA) and multivariate exponent weighted moving average combined with PCA. The results proved the effectiveness of the proposed fault monitoring methods.
papermaking wastewater treatment process; principal component analysis; cumulative sum (CUSUM); exponent weighted moving average (EWMA); fault detection
王龄松先生,在读硕士研究生;研究方向:制浆造纸过程控制。
2017- 04-25(修改稿)
制浆造纸工程国家重点实验室开放基金资助项目(201610);南京林业大学高层次人才科研启动基金(163105996);江苏省制浆造纸科学与技术重点实验室开放基金项目(201530)。
TS79
A
10.11980/j.issn.0254- 508X.2017.08.004
*通信作者:刘鸿斌,副教授;研究方向:制浆造纸过程建模、监测和控制。
