基于改进积分分离PID的LED电源控制系统设计与仿真

丁族桉，许 珩

(兰州空间技术物理研究所, 甘肃 兰州 730000)

基于改进积分分离PID的LED电源控制系统设计与仿真

丁族桉，许 珩

(兰州空间技术物理研究所, 甘肃 兰州 730000)

以电压反馈脉宽调制(PWM)控制模式的数字控制双管正激型LED开关电源为控制对象，设计合理的补偿算法。首先建立开关电源的功率部分模型并对该系统设计了数字PID补偿算法，通过闭环系统仿真分析传统PID算法存在的不足；然后针对数字PID算法存在的超调量过大的问题，以积分分离PID算法为基础，通过建立比例、微分两个增益系数与输入误差之间的函数，设计一种改进的积分分离PID算法；最后在Simulink中进行系统级别的仿真，对分别采用两种补偿算法的系统输出特性进行比较。结果表明：采用改进型积分分离PID算法可以在不改变稳定性以及调节时间的基础上减小超调量，取得更好的控制性能。

LED;积分分离PID；双管正激拓扑；Simulink；电源；控制系统

引言

LED作为照明光源使用时，其伏安特性的非线性，对数字开关电源的控制系统提出了非常苛刻的要求[1]。数字PID前端补偿算法因为结构简单、工作稳定、鲁棒性良好等因素仍被广泛使用。但是随着PID控制技术的发展以及负载对电源控制系统的要求不断提升。出现越来越多适用于不同场合的PID控制方法。

本文所涉及的控制系统部分开关电源采用双管正激DC-DC变换器，控制模式为电压反馈脉宽调制(PWM)，输出电流经200 mΩ反馈电阻R以电压的形式反馈，系统的总体控制框图如图1所示。

目前系统所采用的前端补偿算法为传统的数字PID算法，其稳定性良好。但在系统启动时，会出现超调量过大的问题，系统引入的超调量会使负载在短时间内通过的较大电流值，也会对负载造成一定的冲击，降低系统的可靠性以及负载的寿命。具体原因有以下两点：

图1 开关电源控制框图Fig.1 The switching mode power supply control diagram

1)负载LED的等效电阻为非线性的，这导致开关电源系统在启动过程中为一个时变的，非线性模型。所以传统的线性PID补偿器会使系统的动态性能指标变差。

2)PID补偿器引入的积分环节可以消除静态误差，但由于执行机构的门限值使前期积分累积较大，从而引入较大的超调量。

积分分离PID是当输入误差值较大时，取消积分的作用，仅采用PD控制，当误差值较小时，引入积分环节来消除静态误差[2]。本文会在积分分离PID算法的基础上加以改进，针对系统的非线性特性，建立比例、微分增益系数与输入误差之间的函数，设计一种改进型积分分离PID前端补偿算法。不仅可以消除由上述两个因素引入的较大的超调量，而且不改变系统其余的动态指标以及静态指标。

Simulink/Matlab具有强大的仿真建模和数据运算能力，为设计数字PID算法提供了平台。本文将搭建LED开关电源，以及所设计的改进型积分分离PID算法的Simulink模型并仿真，与传统线性PID算法进行对比，结果证明：改进型积分分离PID算法可以在不改变稳定性以及调节时间的基础上减小超调量，有效改善开关电源系统的控制性能。

1 开关电源的数字PID控制器设计与仿真

LED伏安曲线特性为非线性的，因此在Simulink下需要为其建立专门的模型，由于实际负载为五个LED灯串联而成，因此可建立基于查找表的非线性电阻模块，如图2所示。

其中一阶延迟环节的引入是为了避免在仿真过程中内部运算产生代数环从而降低运算速率。

开关电源功率部分采用双管正激DC-DC变换器，其主要部分的设计参数如表1所示。

前端补偿环节采用数字PID算法，是基于模拟PID控制器的离散化。具体设计步骤如下所述[3]。

模拟PID控制算法的传递函数为

(1)

离散化后，用求和代替积分，用向后差分代替微分，将式(1)离散化为后向Euler法下数字的PID积分器：

(2)

由式(2)可设计基于后向Euler法下的数字PID积分器，其Simulink模块图如图3所示。

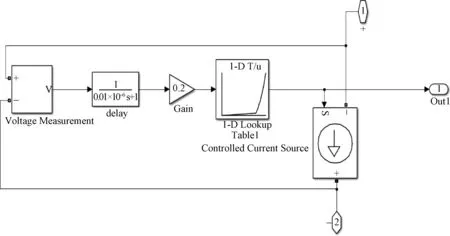
图2 LED负载的Simulink等效模型Fig.2 The Simulink equivalent model of LED load

表1 开关电源功率部分主要设计参数

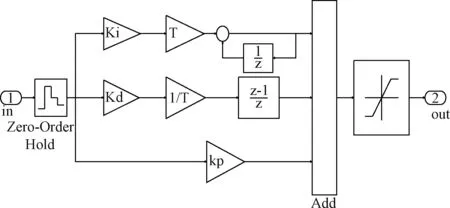
图3 数字PID积分器的Simulink模型Fig.3 Simulink model of digital PID algorithm

最后，建立开关电源控制系统的Simulink模型(图4)，并进行参数整定，参数整定采取试凑法，具体整定方法分为如下三个步骤[4]：

图4 开关电源控制系统的Simulink模型Fig.4 Simulink model of the switching power supply control system

1)先整定比例部分系数，由0逐渐增大，直至系统静态误差最小且刚好不产生震荡。

2)之后不断增大积分系数，消除静态误差，同时适当减小比例系数，防止系统产生震荡。

3)调节微分系数，减小调节时间与超调量，并同时调节比例，积分系数，直至系统的响应曲线达到最佳。

整定后的PID算法中3个系数的取值分别为：

kp=1.3;ki=2×10-6; kd=8 000

基于上述设计，对开关电源系统进行Simulink仿真，控制系统其中步长设置为ode23，仿真时间为0.01 s；示波器scope所显示波形为通过负载的电流值大小。最终系统负载的电流值随时间变化曲线如图5所示。

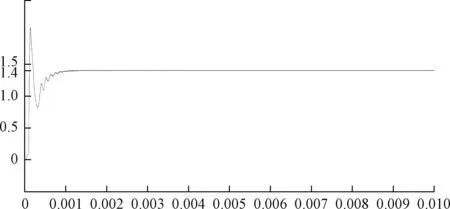
图5 数字PID算法仿真图Fig.5 The simulation of digital PID algorithm

2 改进型积分分离PID算法的设计与仿真

由图5的仿真结果可知：传统PID算法会使系统在启动过程中超调量过大。传统PID算法引起超调量过大是由于负载的非线性以及积分项积累两个因素引起的。大量文献[5-8]采用积分分离PID算法：当输入误差值较大时，取消积分的作用，仅采用PID控制；当误差值较小时，引入积分环节来消除静态误差，可以有效解决积分项累积造成的超调量过大的问题[9-10]。本文会对积分分离PID算法进行改进，进一步改善系统的超调量。

PID控制算法中比例项使系统响应速度加快，减小静态误差，但同时也增大系统超调量；微分项使系统响应速度加快，减小超调量，但会使系统产生振荡[5]。因此，建立3个误差门限值εP、εi、εd。比例、微分、积分系数kp、ki、kd的取值规律以及作用如表2所示。

表2 PID增益系数取值规律

根据上述取值规律，通过建立门限值以及相应增益系数并调整，最终可建立关于误差值与比例、微分系数之间的分段函数，结合积分分离PID算法可得最终kp、ki、kd关于误差值ek的函数如式(3)～(5)所示。

比例系数kp：

(3)

微分系数ki：

(4)

积分系数kd：

(5)

根据上述所设计的算法建立其相应的Simulink模型(如图6所示)，代替传统PID补偿器并进行仿真。仿真波形图如图7所示。并与传统数字PID算法控制效果进行对比。控制性能指标对比如表3所示。

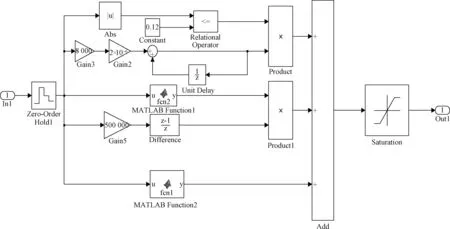
图6 改进型积分分离PID算法Simulink模型Fig.6 Simulink model of the improved integral separate PID algorithm

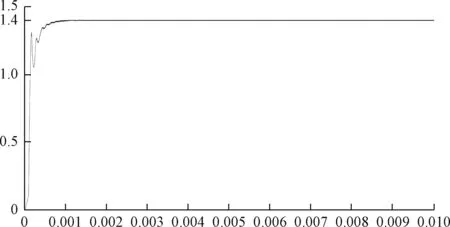
图7 改进型积分分离PID算法仿真图Fig.7 Simulation map of the improved integral separate PID algorithm

表3 两种算法性能对比

3 结论

通过仿真验证可知：采用改进型积分分离PID算法不仅可以在不改变系统的稳定性与响应时间的前提下大幅度减小系统启动时的超调量，而且还可以使曲线过渡平稳，使负载避免短时间内通过过大的电流值，提升了系统的可靠性，具有一定的工程应用价值。

[1] 金永镐,金楠. 同步斩波式开关LED照明灯恒流驱动电源设计[J].电源技术，2013,37(8):1417-1421.

[2] 王勇.非线性PID控制的研究[D].南京：南京理工大学，2000.

[3] 薛定宇.控制系统计算机辅助设计[M].北京：清华大学出版社，2005.

[4] YOUSEFZADEH Vahid， CHOUDHURY Shamim.Nonlinear Digital PID Controller for DC-DC Converters.IEEE Applied Power Electronics Conference and Exposition,2008.

[5] 谢应孝. Buck型DCDC开关电源的研究与设计[D].哈尔滨：黑龙江大学,2010.

[6] 李春燕. 基于DSP的电源数字控制研究[D]. 南京：南京航空航天大学，2004.

[7] 黄博. 60W双管正激电源的数字与模拟控制研究[D].杭州：杭州电子科技大学，2012.

[8] 邵同盟.新型开关电源控制方法研究.电工技术，2015，9：94.

[9] 沈学锋，李浩光. 基于PWM控制的开关电源设计. 自动化与仪器仪表，2017，(4)：34.

[10] 赵赫. 关于DSP的数字PID控制在开关电源中的探讨. 工业，2017，1：13.

Design and Simulation of Improved Integral Separate PID Algorithm Used on LED Source Control System

DING Zu’an，XU Heng

(LanzhouInsitituteofPhysics,ChineseAcademyofSpaceTechnology,Lanzhou730000,China)

In this paper, a reasonable digital PID algorithm is designed for the dual switch forward LED which is in voltage feedback PWM (pulse width modulation) control mode. At first, part of the model is established for the switching mode power supply and digital PID algorithm is designed for the system. The close loop system simulation analysis is used to analyze the shortcomings of the traditional PID algorithm. Aiming at the high overshoot of digital PID algorithm, an improved integral separate PID algorithm is designed by establishing the function with input error and gain coefficients of proportion and differential. System level simulation is conducted in Simulink to compare the output characteristics of the two compensation algorithms. The result show that improved integral PID algorithm can decrease overshoot of the system without changing stabilization and regulating time and get better control performance.

LED; integral separate PID; dual switch forward topology; Simulink; power supply; control system

TM923

A

10.3969/j.issn.1004-440X.2017.04.017