共振型低频振荡扰动源定位方法综述
2017-09-14周榆晓
周榆晓,刘 旸,刘 璐
(1.国网辽宁省电力有限公司电力科学研究院,辽宁 沈阳 110006;2.国网辽宁省电力有限公司计量中心,辽宁 沈阳 110168)
共振型低频振荡扰动源定位方法综述
周榆晓1,刘 旸1,刘 璐2
(1.国网辽宁省电力有限公司电力科学研究院,辽宁 沈阳 110006;2.国网辽宁省电力有限公司计量中心,辽宁 沈阳 110168)
共振型低频振荡是较常见的一种低频振荡,当发生共振型低频振荡时,迅速找到扰动源的位置并能有效切除,对电网的稳定安全运行有重大意义。文中对扰动源定位的3种方法进行研究,比较各自的优缺点,提出共振型低频振荡扰动源定位的新策略,该策略可根据电网实际情况选择定位方法对扰动源进行准确定位。
低频振荡;扰动源定位;能量函数;混合动态仿真;行波延时
电力系统是非线性动态系统,其运行的稳定 性和安全性是电能生产的重要保证。由于我国的能源与负荷的集中地区相距远,需要通过各区域电网的互联来完成电力输送,使我国电网越来越复杂,规模越来越庞大,导致电网中低频振荡时有发生。低频振荡的频率范围是0.2~2.5 Hz[1],目前研究最多的低频振荡机理为负阻尼机理、共振机理、分岔机理和混沌机理[2],按振荡模式又分为区间振荡和区内振荡。负阻尼机理引发低频振荡得到广泛证明,负阻尼机理的本质是高倍数快速的励磁调节器在发电机组中的大量使用造成电力系统中产生负阻尼,进而导致整个电力系统的阻尼值变得很小,严重时为负数,提高电力系统的正阻尼可以抑制低频振荡的发生,研究发现通过在发电机组加装电力系统稳定器(power system stabilizer ,PSS),可以达到此效果[3-4],但实际运行时,虽然装设了PSS但振荡依然发生,共振型低频振荡可以很好地解释该现象[5]。1996年8月10日,美国西部大停电事故[6]中,就是因为出现了0.28 Hz的负阻尼低频振荡。2005年5月13日和8月18日南方电网、2005年9月1日华中电网[7]、2011年11月云南电网发生的功率振荡现象都可以较好地用共振型低频振荡机理解释。
研究表明,当发电机侧或负荷侧存在周期性扰动[8]且这种扰动频率接近系统的自然频率时,会发生共振型低频振荡,这种振荡具有起振快,切除扰动源振荡快速衰减[9],系统可以恢复安全稳定运行的特点。目前,对于扰动源定位的方法有3种:能量函数法[10],混合动态仿真法[11],行波延时法[12]。
1 能量函数法
文献[13]从能量角度描述了共振型低频振荡的机理。由于电力系统强迫功率振荡是由扰动源的周期性扰动引发的[14],带有扰动源的负荷或者发电机组在振荡过程中能量的变化与其他的负荷或者发电机组有明显差别,通过运用能量函数可以观察负荷或者机组以及线路的能量变化,进而来判断扰动源所在的位置[15]。
能量函数的推导过程[10]如下,采用单机无穷大系统,对发电机采用经典模型:
(1)
对其首次积分:


(2)
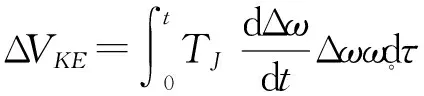
在多机系统下,扰动源注入系统的能量等于系统耗散的能量。然而,当扰动源作用于某台发电机时,扰动源注入的能量一部分转化为该机组的势能,另一部分被阻尼耗散掉。由于扰动源注入的能量不能够完全被阻尼耗散掉,这就使得此发电机组的势能不断增加。由于势能不能完全转化,增加的势能会通过输电线路流入网络,通过输电线的传播将能量传给其他发电机组。线路为补偿自身能量消耗,势能必然增加。不存在扰动源的发电机组为了平衡流入的势能,阻尼耗能不断增加,造成不存在扰动源的发电机组的势能减少。整个系统振荡过程中,扰动机组的势能不断增加,而不存在扰动源机组的势能则不断减小。
(3)
(4)
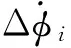
系统内部存在两种能量转化过程:各台发电机动能与其自身势能的周期性能量转化的过程;注入的能量在网络中传播,并被各个耗能元件消耗的过程。第二个过程能够反映出势能在整个网络中的流动方向,可以通过判断能量的流动方向来判定扰动源的位置。能量函数法实现流程如图1所示。
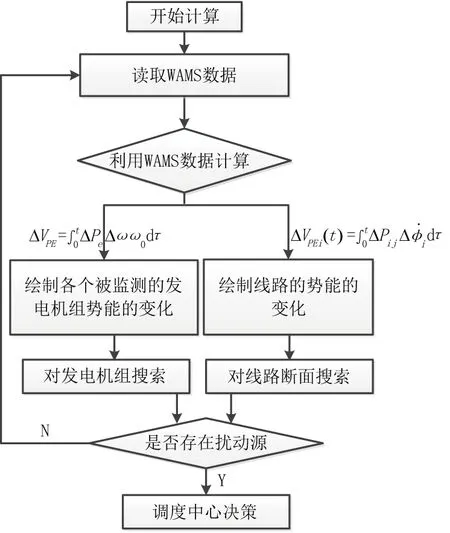
图1 能量函数法实现流程图
2 混合动态仿真法
混合动态仿真理论源于动态等值和电路叠加原理,该方法最初被用于模型和参数的有效性验证及定位仿真误差源[16]。它为仿真结果与实际测量的对比提供平台,为传统的动态仿真提供实际数据接口,将仿真和实际测量数据结合起来对电网进行分析,更深层次挖掘实际数据包含的各种信息。
2个区域联网解耦示意如图2所示:假设A区域到B区域的联络线母线上装有PMU装置,在系统发生扰动时,母线上相应的电气量被记录。若A区域为感兴趣的区域,通过母线注入数据可以将B区域等值掉,再对A区域仿真,然后比较仿真结果与实测数据。多个区域联网解耦示意如图3所示。
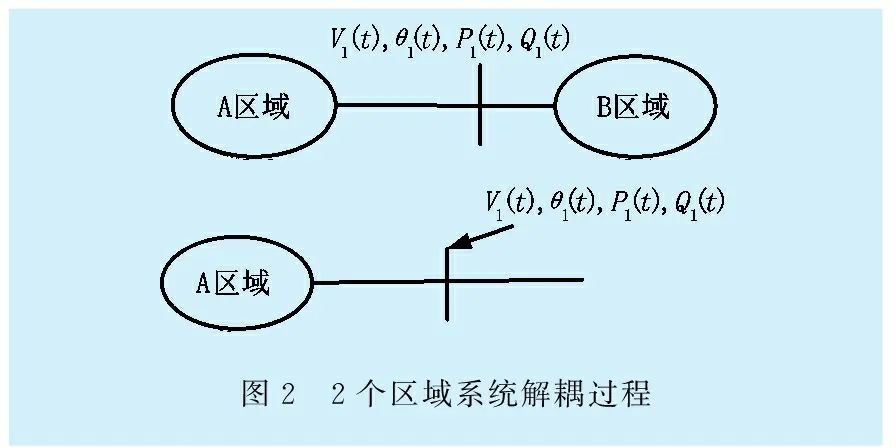
图2 2个区域系统解耦过程

图3 多个区域系统解耦过程
只要母线注入的电气量是WAMS的实际测量量,则对于保留的1区域来说,无论被等值的区域包含多么复杂,都可以被等效替换掉,从而实现电网的1区域与其他区域的解耦。
把等效掉的区域建立成无穷大电源串联移相变压器的模型,如图4所示。此时将PMU中母线2的实际数据作为移相变压器的注入。
在实际操作中,就是在每一个仿真步长利用理想变压器T来控制母线2的电压幅值和电压相角,从而实现动态等值。

图4 等值过程
变压器变比和移相的公式为
(5)
式中:E=1∠0°=1;δ=0°;E为单机无穷大电源测的电压;δ为单机无穷大电源测电压相角;Vrcd、θrcd分别表示WMAS记录的电压幅值和电压相角。
当系统中共振型低频振荡扰动源定位系统启动后,对电网进行解耦,采用混合动态仿真对扰动源定位。
当现场响应与仿真响应基本一致时,说明研究的区域不存在扰动源头;当系统仿真响应与现场响应不一致时,研究的区域存在扰动源。混合动态仿真法实现流程如图5所示。
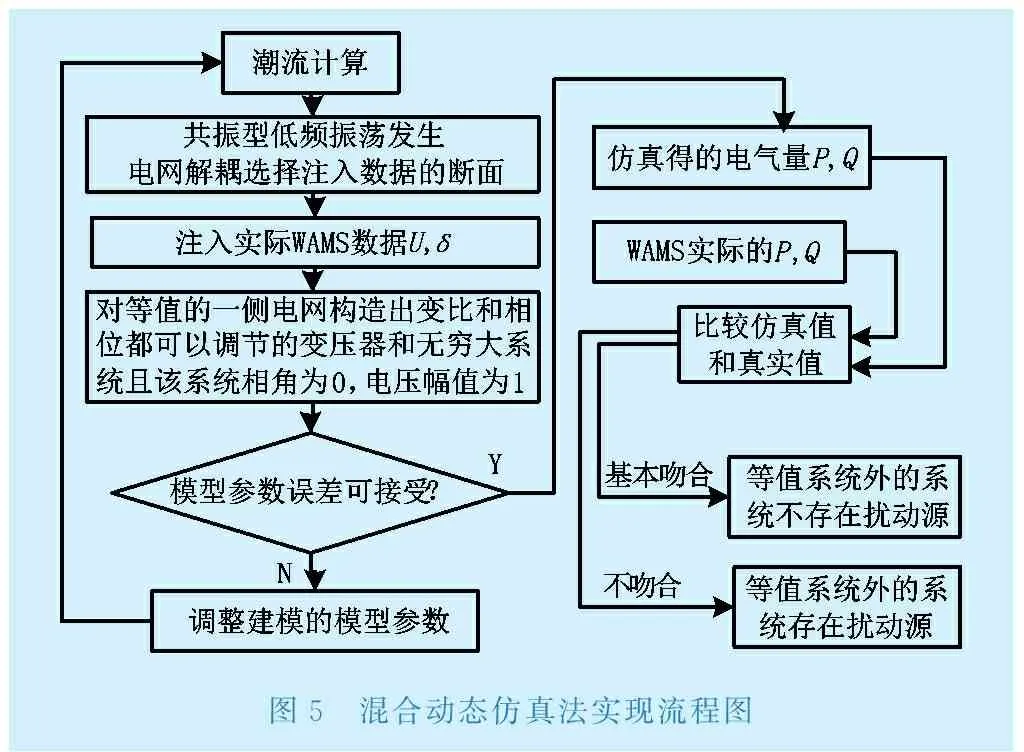
图5 混合动态仿真法实现流程图
3 行波延时法
3.1提取低频振荡扰动变量的希尔波特变换
我国电网工频为50 Hz,低频振荡的频率范围是0.2~2.5 Hz,发生共振型低频振荡时,可用式(6)表示含有扰动量的工频电压变量:
u(t)=a(t)cos(ωt+φ)
(6)
利用希尔波特变换(hilbert transform,HT)[12]可以对低频扰动量a(t)进行提取。令v(t)与u(t)共轭且正交,则HT变换可表示为
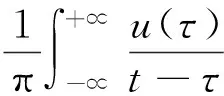
(7)
v(t)是一个与u(t)相类似的正弦函数信号,即:v(t)=a(t)sin(ωt+φ),再将v(t)与u(t)组合起来构建一个复合信号。
z(t)=a(t)cos(ωt+φ)+ja(t)sin(ωt+φ)
(8)
即:
z(t)=a(t)ej(ωt+φ)
(9)
式(9)复信号的模值就是扰动变量a(t),即扰动变量a(t)计算公式为

(10)
3.2计算扰动行波传播延时时间的方法
当发生共振型低频振荡时,扰动源所在点的电压发生畸变,该畸变中具有特殊形状的电压行波会通过输电线路传播。由于电网规模庞大、输电线路距离长,在传播过程中,该特殊形状的扰动行波必然产生延时,同时,不同安装位置的测量装置测到的行波应具有类似的特性。
把2个不同安装位置测量装置测量到的电压波形进行对比分析,算出该特殊形状波形在2个测量装置安装位置之间输电线路的传播延迟时间。
在电力系统中不同地点安装2个测量装置,分别为测量装置A和测量装置B,当发生共振型低频振荡时,测量装置A和B在事前设置的时间t内,相同时刻测量的电压信号分别为fVA(τ)和fVB(τ)(τ∈[0,t]),在测量装置A和B内,为了得到对应的扰动分量fHVA(τ)和fHVB(τ),对测量装置测得的电压信号分别进行HT变换,并把提取的信号实时发送给相应的监控装置。在监控装置内,把顺序相关度的函数定义为式(11)和(12)。
(11)
(12)
令RAB-MAX为[0,t]时间范围内RAB(x)的最大值,RBA-MAX为[0,t]时间范围内RBA(x)的最大值;若RAB-MAX>RBA-MAX,则测量装置A首先测量到特殊形状的扰动行波,测量装置B随后测量到该行波,在RAB(x)中,RAB-MAX对应的xMAX(RAB)值乘以采样周期等于2个测量装置安装点测量到信号的时间间隔ΔTAB(s),即特殊形状的扰动行波被电力系统中测量装置A安装点与测量装置B安装点测量到的时间间隔(延时时间)为
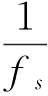
(13)
式中:fs为采样频率(Hz)。
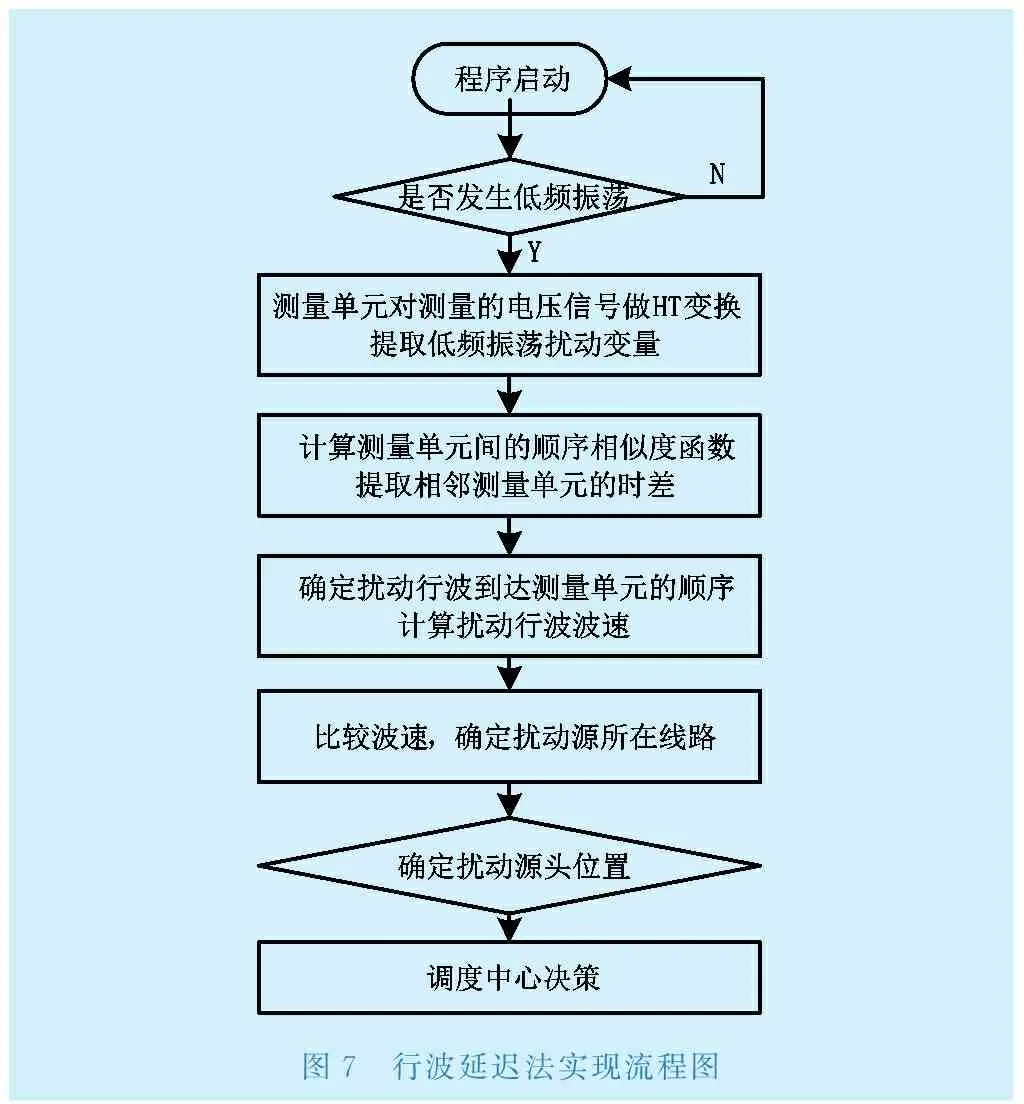
反之,若RAB-MAX 3.3定位方法 扰动源施加在A和B测量单元之间且靠近A测量单元侧。测量单元之间的线路长度如图6所示。 图6 系统示意图 由于扰动行波在不含扰动源线路上的波速基本一致,Cd为扰动行波的波速: (14) 对于扰动源所在线路则存在: (15) 则扰动源所在的位置距离A测量单元的距离: s=lAB-ΔTABCd/2 (16) 行波延迟法实现流程如图7所示。 图7 行波延迟法实现流程图 4.13种定位方法缺点 a. 能量函数法 观察由能量函数法求出的势能曲线可较为直观地定位到扰动源,准确率高,但采用此方法定位时,需要人为参与并决策。若系统结构较为复杂,线路和节点个数非常多时,系统发生共振型低频振荡,定位过程耗时长,而且定位过程中系统的运行状况可能变得更为恶劣,不利于系统的安全稳定运行。 虽然研究人员已经构造出能量函数,但没有给出明确的定量判据,并且能量函数法源于李雅普诺夫直接法,分析结果偏于保守。 b. 混合动态仿真法 由于各个区域电网的互联,涉及的元件复杂且类型众多,在建模时,参数以及模型与实际情况可能存在差异。而混合动态仿真法有效性对模型和参数的准确性依赖性较高[16],如建模不当或者参数准确度达不到要求,混合动态仿真的准确性会受到影响,且混合仿真曲线与实际曲线的误差范围没有定量标准。 混合动态仿真法对电网的解耦方案需要依据系统中PMU的安装地点,如果扰动源是小水电机组以及未安装PMU的机组,在定位时,只能定位到某个区域,而不能准确定位到某个具体机组或者负荷。 c. 行波延时法 该方法所需的采样测量单元数量少,可节省大量投资。但是该方法利用了希尔伯特变换,这种变换对实测信号的处理时存在一些问题。实测信号中几乎都存在噪声,会使很多原来满足希尔伯特变换条件的信号无法完全满足,当实测信号波动非常大时,该信号是一个非平稳的数据序列,希尔伯特变换得到的结果很大程度上失去了原有的物理意义。这些缺陷大大影响扰动源定位的准确性。 4.2对比分析 3种定位方法都有准确的理论基础。能量函数 法应用需要同时有很多测量单元来提供数据,相对比较复杂,混合动态仿真法应用时只需要单个测量单元的数据,这是混合仿真法的优势。行波延时法需要的测量单元少,与前2个方法比较设备的投资较少,但在计算行波波速时,由于系统的噪声以及其他干扰,波速计算可能出现误差,实测数据的好坏对于进行HT变换的有效性影响很大。3种方法从求解方法、定位判据的比较见表1。 表1 3种定位方法对比 共振型低频振荡扰动源定位的能量函数法、混合动态仿真法和行波延时法在使用过程中都存在局限性。所以当电网中发生共振型低频振荡时,需要根据电网的特性确定适用的方法。当电网具有先进的测量装置时,首选行波延时法;当电网建模准确且对扰动源定位精度要求高时,首选混合动态仿真法;当电网规模较小时,首选能量函数法。该策略的流程图如图8所示。 图8 共振型低频振荡扰动源定位策略流程图 本文对共振型低频振荡的机理、危害进行了介绍,明确了迅速定位并切除扰动源对保证电力系统稳定运行的重要性。对3种扰动源定位的方法原理进行了推导,对定位的流程进行了描述,分析并比较了每种方法的优缺点,并提出一种共振型低频振荡扰动源定位的新策略。该策略可以根据电网实际情况选择合理的定位方法对扰动源进行准确定位。新策略逻辑简单,方便实用,适应性强,对于保障电网安全稳定运行具有一定作用。 [1] 倪以信,陈寿孙,张宝霖.动态电力系统的理论与分析[M].北京:清华大学出版社,2002:260. [2] 薛禹胜,周海强,顾晓荣.电力系统分岔与混沌研究述评[J].电力系统自动化,2002,26(16):9-15. [3] 陈冬霞.大电网低频振荡研究及其最新进展[J].东北电力技术,2012,33(11):33-37. [4] 范 伟,赵书强.风电场接入电网强迫功率振荡研究[J].东北电力技术,2009,30(1):36-39,48. [5] Juan M.Ramirez A,Rodrigo Garcia Valle.A technique to reduce power systems electromechanical models [J].IEEE Trans on Energy Conversion,Vol.19,No.2,June, 2004. [6] 何大愚.对于美国西部电力系统1996 年7 月2 日大停电事故的初步认识[J].电网技术,1996,20(9):35-39. [7] 周 密.南方电网低频振荡仿真研究[D].北京:华北电力大学,2008:33-35. [8] 汤 涌.电力系统强迫功率振荡的基础理论[J].电网技术,2006,30(10):29-33. [9] 王铁强.电力系统低频振荡共振机理的研究[D].北京:华北电力大学,2001:37-41. [10] 余一平,闵 勇,陈 磊,等.基于能量函数的强迫功率振荡扰动源定位[J].电力系统自动化,2010,34(5):1-6. [11] 薄 博.电力系统混合动态仿真综述[C].中国高等学校电力系统及其自动化专业第二十四届学术年会论文集,2008:2 325-2 328. [12] 董 清,梁 晶,颜湘武, 等.大规模电网中低频振荡扰动源的定位方法[J].中国电机工程学报,2012,32(1):78-83. [13] 韩志勇,贺仁睦,徐衍会, 等.基于能量角度的共振机理电力系统低频振荡分析[J] .电网技术,2007,31(8):13-16. [14] 余一平,闵 勇,陈 磊, 等.多机电力系统强迫功率振荡稳态响应特性分析[J].电力系统自动化,2009,33(22):5-9. [15] 韩志勇,贺仁睦,马 进, 等.电力系统强迫功率振荡扰动源的对比分析[J].电力系统自动化,2009,33(3):16-19. [16] 杨俊新,马 进,陶 华.基于电力系统混合仿真的低频振荡误差校正策略[J].电力系统自动化,2010,34(8):20-23. Survey on Disturbance Localization of Power SystemLow-frequency Oscillation of Resonance Mechanism ZHOU Yuxiao1,LIU Yang1,LIU Lu2 (1.Electric Power Research Institute of State Grid Liaoning Electric Power Co.,Ltd.,Shenyang,Liaoning 110006,China;2.State Grid Liaoning Electric Power Co.,Ltd.,Metrological Center,Shenyang,Liaoning 110168,China) With the expansion of the internet-scale of the grid and the advancement of area inter-connection, the probability of occurrence of low-frequency oscillation continuously increases.Low-frequency oscillation of resonance mechanism which has the characteristics of quick start vibration is one kind of low-frequency oscillation.It can quickly converge if the disturbance source is soon removed. When low-frequency oscillation occurs, it is utmost important for the security and stability of power system to find disturbance source and remove it in time. This paper studies three methods of disturbance localization and compares their advantages and disadvantages. At last the article puts forward a new strategy for localization of power system low-frequency oscillation. According to the condition of grid, this strategy will choose one of the methods to locate low-frequency oscillation. low-frequency oscillation;disturbance localization;energy function;hybrid dynamic simulation;wave delay TM712 A 1004-7913(2017)08-0006-05 周榆晓(1988),男,硕士,助理工程师,从事高电压技术工作。 2017-05-07)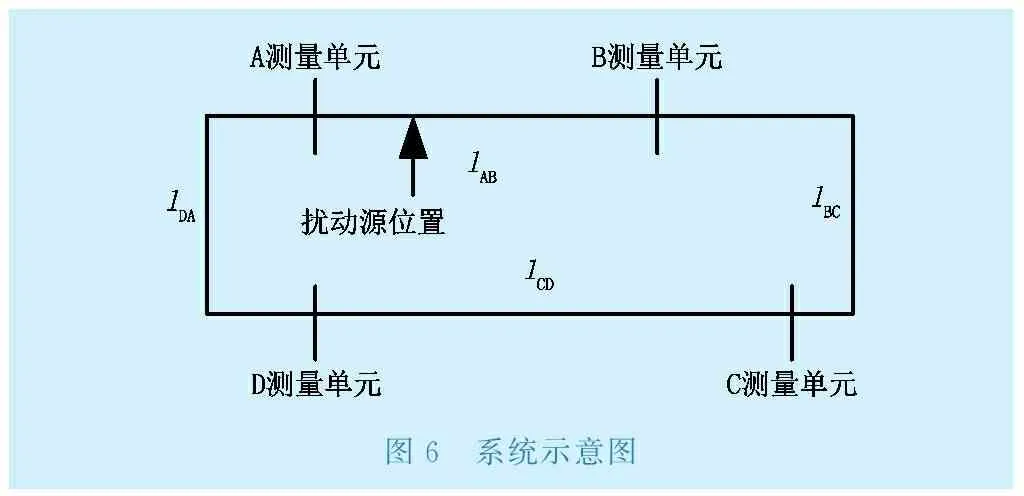
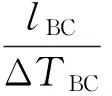
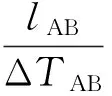
4 3种定位方法对比分析

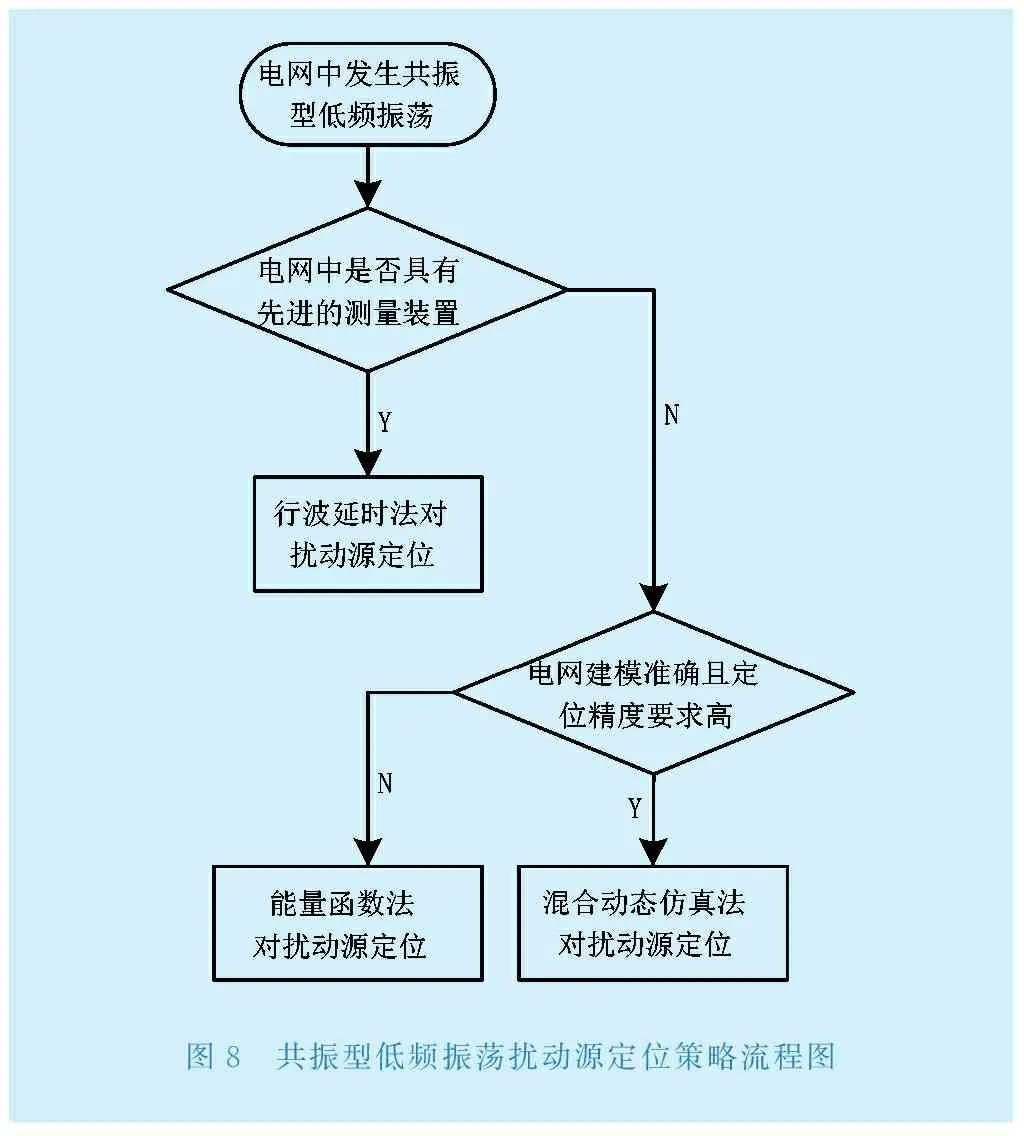
5 共振型低频振荡扰动源定位的新策略
6 结束语
