基于CQC算法的大跨屋盖结构风致响应研究

赵晓红 李秋胜 陈伏彬

1国家知识产权局专利局专利审查协作河南中心（450000）2湖南大学土木工程学院（410082）3香港城市大学土木及建筑工程系（100013）

基于CQC算法的大跨屋盖结构风致响应研究

赵晓红1李秋胜2，3陈伏彬2

1国家知识产权局专利局专利审查协作河南中心（450000）2湖南大学土木工程学院（410082）3香港城市大学土木及建筑工程系（100013）

笔者以大跨屋盖结构的风洞测压数据为基础，基于CQC快速算法理论编写了Matlab风致响应计算程序。计算风致响应时同时考虑了风荷载谱的实部和虚部对风致响应的贡献，能够有效准确的判定参振模态数、模态耦合项、以及背景共振相关系数。

大跨屋盖；参振模态数；模态耦合效应；位移响应谱；背景共振相关性

0 引言

近年来，大跨屋盖结构得到越来越广泛的应用，这类结构通常质量轻，柔性大，阻尼小，自振频率低，风荷载往往成为这类结构设计的主要控制荷载。屋盖结构的自振特性及风致响应计算特点与高层结构有明显区别，不能把研究较为成熟的高层风致响应分析理论直接用于屋盖结构。对于大部分屋盖响应分析，必须考虑高阶模态的贡献且模态耦合效应不能忽略，这导致风致响应比较复杂。

屋盖结构的风致响应计算主要有时域算法、频域算法以及各种非线性随机振动分析方法。时域算法采用直接将风洞试验获得的风荷载时程加在结构上进行瞬态分析的方法,抛弃了准定常假定,因而能够获得较为精确的计算结果，但其缺点是计算量大、过程复杂，故不便在工程上广泛应用。频域分析法通常以模态分解为基础，对于每一阶模态，将风速谱通过气动导纳转化为风压谱，或者直接通过风洞试验获得风压谱，通过机械导纳函数得到结构的响应谱，然后通过积分获得根方差响应。此法计算过程简单，物理意义明显，且耗费的计算资源较少，所以目前主要采用频域法进行结构的风致响应计算。

频域算法主要包括模态位移法、模态加速度法以及背景共振分量叠加法，后来又有学者提出了多阶模态力法[1~4]。在模态位移法中，通常是通过完全二次型组合法（CQC，Complete Quadratic Combination）来对各阶模态响应进行组合，并考虑模态间的耦合，求得精确的总响应。由于一般精确的CQC法计算量大，所以在实际复杂结构的风致响应计算中，常忽略振型的交叉项而得到近似的平方法和开方法（SRSS，Square-Root-Sum-Square）[5]。为了减少大量的数值运算，同时使得脉动响应的物理意义更加明确，风工程学者将总脉动响应分为背景和共振分量的组合形式[6~7]，但背景和共振分量之间的耦合作用常被忽略。陈波[8]从时域上定义了结构响应的背景分量和共振分量，提出了考虑背景和共振分量耦合的风致响应计算方法。柯世堂[9]提出了考虑背景、共振以及背景共振交叉耦合项的风致响应计算方法。

1 程序简介

基于CQC快速算法理论[10]，笔者运用Matlab编写了屋盖结构风致响应的计算程序，包括CQC法、SRSS法、多阶模态力法，其中CQC法考虑了振型的交叉项。

2 算例

一大跨度平板式网壳结构，如图1所示。结构参数为:长宽各40 m，底裙高20 m，四边简支，材料的弹性模量=2.061 011 N/m2，密度=7 850 kg/m3，泊松比=0.31，屋面质量取62.5 kg/m2，阻尼比设为= 0.02，采用比例阻尼。对该屋面进行1:100的几何缩尺比制作刚性模型进行风洞试验，获得各测点的风压时程，风洞流场模拟A类地貌（=0.12）的风速剖面和湍流度剖面，屋面上共布置400个测点，各测压管长度一致均为80 cm，采样频率为312.5 Hz，采样时长32 s。

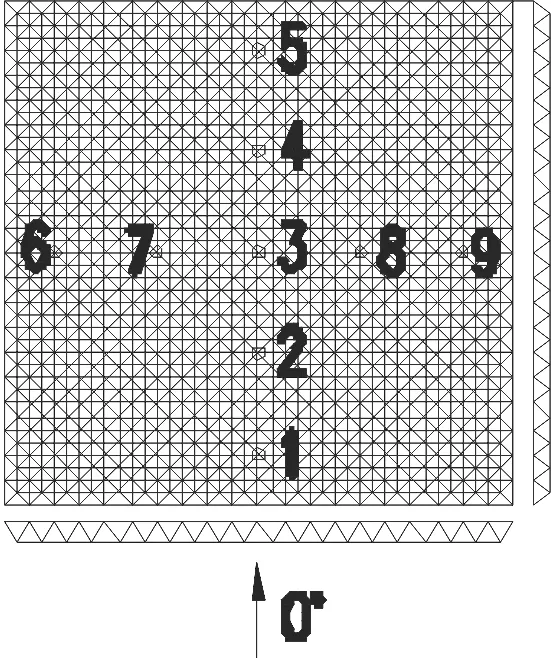
图1 平板网架屋盖示意图

对该屋盖建立有限元模型，通过模态分析得到屋盖结构前10阶自振频率分别为:2.72 Hz、5.09 Hz、5.09 Hz、6.60 Hz、10.58 Hz、10.72 Hz、10.84 Hz、10.84 Hz、11.51 Hz、11.51 Hz，可见频率分布比较分散，为确保计算结果尽可能接近实际值，计算参振模态数取前50阶。

表1 屋盖结构风致响应不同方法计算结果比较（Z向平均位移单位:mm）

表1给出了运用Matlab程序与通用有限元软件计算的位移平均值的比较,从表1可以看出，二者计算的结果非常接近或者完全一致。

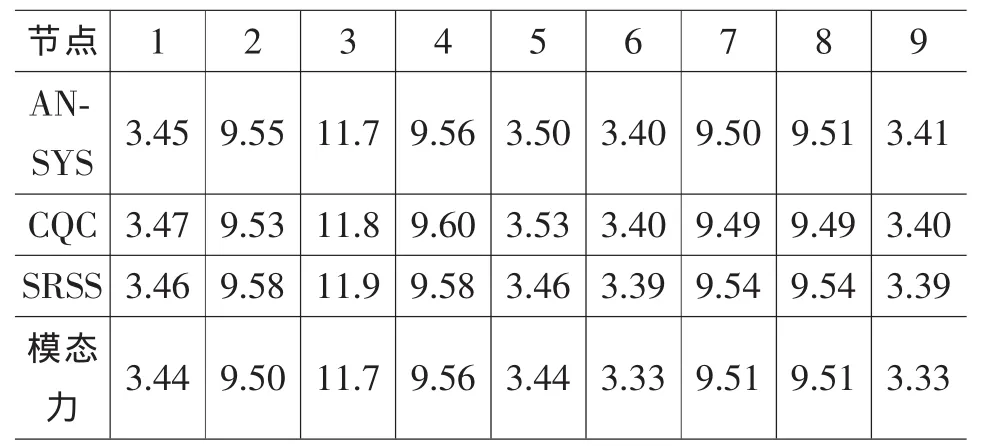
表2 屋盖结构风致响应不同方法计算结果比较（Z向脉动位移单位:mm）

表2给出了运用Matlab程序与通用有限元软件计算的位移脉动均方根值的比较。从表2可以看出:1）时域方法和频域方法计算的结果非常接近。2）分别计算各频域法与ANSYS法的相对误差，然后再对相对误差的绝对值取平均，通过该平均值可衡量出各频域算法与时域算法的差异大小，CQC法、SRSS法、模态力法的计算结果与ANSYS的计算结果平均误差分别为2.11%、3.67%、3.22%。可见，SRSS法与ANSYS法的误差最大，CQC法与ANSYS法的误差最小，但总的来说，上述几种频域算法的计算结果都具有较高的精度，同时证明了笔者编写的程序是正确有效的。

表3给出了运用CQC法和SRSS法计算风致响应的结果对比，CQC法和SRSS法的主要差别在于是否考虑模态耦合项的影响。从该表可以看出，与CQC法相比，SRSS法有可能高估也有可能低估风致响应的脉动值，但差值较小，最大误差仅为-1.99%，对于本算例（屋盖跨度仅为40 m）来说可以忽略模态耦合项的影响，但是对于特大型的大跨屋盖结构（屋盖跨度>120 m），模态耦合项的影响是否能够忽略，还需通过计算分析之后才能确定，后续会对此内容做进一步的研究。

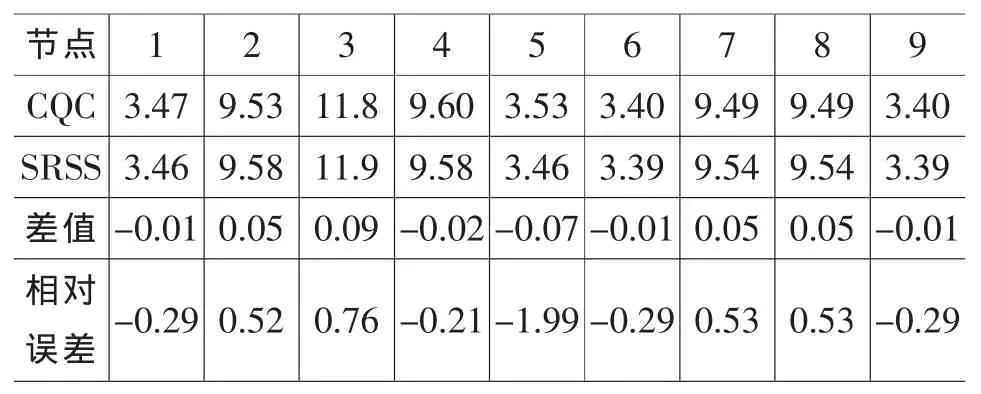
表3 SRSS算法与CQC算法的差别（Z向脉动位移单位:mm）

3 结语

在实际研究中，基于笔者编写的CQC算法程序,将其应用于特大型屋盖结构（屋盖跨度>120 m）,计算风致响应的同时考虑了风荷载谱的实部和虚部对风致响应的贡献，能够准确有效地判定参振模态数、模态耦合项以及背景共振相关系数等的影响，同时能够显著缩短程序运行时间，为今后大跨屋盖结构风致效应的分析研究提供了参考。

[1]楼文娟,杨毅,庞振钱.刚性模型风洞试验确定大跨屋盖结构风振系数的多阶模态力法[J].空气动力学学报,2005, 23(2):183-187.

[2]Yasushi U,Motohiko Y,Akinori K.Design wind loadsfor structural framesofflat long-span roofs:Gust loading factor for the beamssupporting roofs.Journal of Wind Engineering and Industrial Aerodynamics,1997,66:35-50.

[3]Yasushi U,Motohiko Y,Akinori K.Design wind loadsfor structural framesofflat long-span roofs:Gust loading for a structurally integrated type.Journal ofWind Engineering and Industrial Aerodynamics,1997,66:155-168.

[4]Yasushi U,Keisuke W,Akihiro S,et al.Wind-induced dynamic response and resultant load estimation ofa circular flat roof.Journal ofWind Engineering and Industrial Aerodynamics,1999,83:251-261.

[5]黄本才,汪从军.结构抗风分析原理及应用(第二版)[M].上海:同济大学出版社,2008.

[6]Davenport A G.The generalization and simplification of wind loadsand implicationsfor computational methods. Journal of Wind Engineering and Industrial Aerodynamics, 1993,46:409-417.

[7]Davenport A G.How can we simplify and generalize wind loads.Journal ofWind Engineering and Industrial Aerody-namics,1995,54:657-669.

[8]陈波.大跨屋盖结构等效静风荷载精细化理论研究[D].哈尔滨:哈尔滨工业大学,2005.

[9]柯世堂,葛耀君.基于一致耦合法某大型博物馆结构风致响应精细化研究[J].建筑结构学报,2012,33(3):111-117.

[10]李方慧.大跨屋盖结构实用抗风设计[M].哈尔滨:黑龙江大学出版社,2008,8.

国家自然科学重大研究计划（91215302）。

资助: