由一道古题引发的新思考

贾蓓蓓

数学是思维的体操，初中数学教学，就要引领学生在思维领域里学习、磨练、提升。在数学学科课堂教学中，有一道古老而又有趣的题目在我心中留下很深的印象，带给我许多思考与感悟。

我国古代许多数学的发现都曾位居世界前列，其中“杨辉三角”（图一）就是一例。杨辉，字谦光，南宋时期杭州人，在他所著的《详解九章算术》一书中，辑录了一个如下图所示的三角形数表，称之为“开方法本源图”。经过观察研究发现，两腰上的数都是1的前提下，杨辉三角有许多重要的特点。例如每个数均为其上方左右两数之和等等。

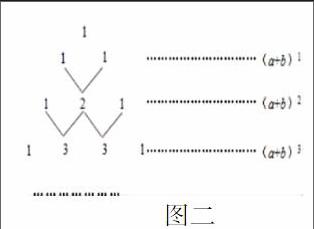
如图二，某同学发现杨辉三角给出了给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律.例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）2=a2+2ab+b2展开式中的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）3=a3+3a2b+3ab2+b3展开式中的系数.

（1）通过观察，请你写楚杨辉三角具有的任意两个特点（阅读材料中的特点除外）

（2）计算：25-5×24+10×23-10×22+5×2-1

（3）请你直接写出（a+b）5的展开式。

点评：本题考查了完全平方公式，学生的观察分析逻辑推理能力，读懂题意并根据所给的式子寻找规律，是快速解题的关键。

学生的做题结果：对于班级中前10名左右的同学解答基本没有问题，而对于多数的同学（1）问还可以，后面的就不知道如何下手。但是老师讲解后，好多学生说很简单啊。从中可以反映出学生的观察分析能力在前面的学习中并没有很好的培养起来，他们只会跟着老师的节奏，按照老师设计的思路去解决问题，没有自己的想法。

那么，如何在平时的教学中培养学生的分析问题、解决问题的能力？我有三点思考：

第一、数学教师要重视数学文化的传播

《义务教育数学课程标准》教材编写建议指出：“数学文化作为教材的组成部分，应该渗透在整套教材中。”例如在数学教材中有华罗庚、我国古代重要的数学著作《九章算术》，以及“贾宪三角”“古建筑中的旋转对称图形——从敦煌洞窟到欧洲教堂”等等。这些材料能帮助学生了解数学在人类发展中重要作用，还可以激发学生学习数学的兴趣，感受数学的严谨性，欣赏数学的美。

而在以前在数学教学过程中，我对于数学文化部分不够重视，常常一笔带过，导致学生在面对数学文化知识时十分棘手，感觉这些题目深奥难懂，无从下手。这就启示我们，在数学教学中，教师应该注重数学文化的渗透，充分引导学生感受古人智慧、继承优秀文化、陶冶自身心灵，以发挥数学课程的育人功能。教师要引导学生通过查阅资料、阅读中外数学名著和数学家的故事、关注数学的发展等途径，从历史、现实、发展等多方面了解数学文化，让数学课堂承载继承与传播数学文化的的大课堂，从而热爱数学、理解数学、体会数学的价值。

第二、数学教师要重视数学知识体系的构建

在这道题目中，呈现的不仅是简单的数字，而是由图形、数字到包含规律的综合表达。对于第一问只要学生认真观察图一就可以看到：首先是形状来说几何中的三角形，这时从三角形的角度出发，就可以找到它的特点；其次从代数的角度观察数之间的关系，也可以很清楚的看到它的特点。而对于二、三问来说：（a+b）=a+b，（a+b）2=a2+2ab+b2，（a+b）3=a3+3a2b+3ab2+b3可得（a+b）n的各项展开式的系数除首尾两项都是1外，其余各项系数都等于（a+b）n-1的相邻两个系数的和，由此可得（a+b）4的各项系数依次为1、4、6、4、1；因此（a+b）5的各项系数依次为1、5、10、10、5、1.还要特别注意两个图之间的联系。

这就启发我们，数学教学不仅仅是数学知识的传授，更是数学知识体系的建立；不仅是计算的演练，更是数学知识普遍联系的运用。

首先，要关注数学知识学科内部的知识联系通融性。“数与代数”、“空间与图形”、“统计与概率”、“课题学习”几大领域不是割裂的条块。教师应该引导学生知道知识是有可能以交织在一起的形式出现，如数形结合、数据处理、数学建模等。随着学习内容的不断增多，可在学生头脑中形成完整的认识体系与合理的知识结构，也利于发展学生综合应用知识的能力。

其次，要关注新旧知识之间的联系通融性。比如，逆向思维教学法就是联系新旧知识的最有效的教学方法，对于帮助学生沟通知识之间内在联系的作用是非常显著的。例如在教学切线长定理时，就可以利用课本中切线长定理推导的例图，引导学生找出图中所有的全等三角形，所有的相似三角形，所有的等腰三角形以及所有的垂直关系。这样一面可以使学生深化切线长定理，一面又可以让学生与已学知识构成联系，形成知识链条。这种教学不仅能让学生迅速理解消化刚接受的知识，更能有利于学生构建系统的知识结构图，真正理解和剖析知识与知识之间的内在联系，形成细密的知识网络。

第三、教师要重视培养学生分析解决问题的能力

传统的数学教学，教师设置问题，学生处于被动应答的地位。在教师指令性的提问中，学生按照老师设计好的路线，一步一步到达终点；如果在此过程中，学生有丝毫的偏差，老师会很快地把学生拉回到老师设计的既定轨道中，学生难以有充分展示自我的机会。然而，随着课改的跟进，考试中许多的新题型的出现，需要的是学生成为学习的主體去发现和解决问题，从而要求教师对传统课堂教学模式做出改变和突破。新的课堂设计应该更好解放学生思维，给学生充分展示个性和主动性的机会。所以，教师要转变观念，由重视教师“教”的角色，向重视学生“学”的角色转变。由原来教师设计教学过程向学生参与课堂设计转变，由原来教师讲学生听向学生小组合作探究攻克疑难转变。如：我们在讲解《平方差公式》的过程中，会有检验学生对于公式的特点的掌握情况，在此处可以让学生自己设计题型，教师提出假设性的问题：“如果你是一名老师，如何设计一个题来检验同学们是否掌握平方差公式。”在学生出题的的过程中，既可以让让学生熟练的掌握公式，又可以引导学生自己感悟公式的特征，学会熟练应用公式，给学生主动思考的空间，数学思维得到发展，有利于培养学生用数学的思想去分析问题和解决问题。

由一道古老的数学问题，激起了我对自己数学教学的诸多反思和感悟。我想，我们的数学教学，不仅是让学生获得数学知识，更是要学会运用数学知识解决各种生活问题的能力。这是素质教育的重要内容，也是时代对我们的数学教师提出的要求。在课程改革的过程中，我们每一位老师要以课程标准为导航，把解决问题与数学基础知识和基本技能的发展融为一个过程，让学生在解决问题的过程中学习数学，实现解决问题能力与知识、技能的同步发展。师生要携手，一起去探究数学之奥秘，去体验数学的博大精深之美。（作者单位：山西省临汾市解放路学校041000）endprint