基于模型预测控制的车车协同后端主动防撞研究*
2017-09-12余国宽何锋赵津
余国宽 何锋 赵津
(贵州大学,贵阳 550025)
基于模型预测控制的车车协同后端主动防撞研究*
余国宽 何锋 赵津
(贵州大学,贵阳 550025)
为提高车辆在复杂行车环境下的主动安全性,提出了一种基于MPC在线优化的加速度重分配后端防撞控制算法,该方法通过车间信息交互分配制动减速度使相邻车辆间协同响应,从而避免碰撞的发生。研究表明,通过车间协同响应避撞,可缓解车辆的减速制动压力,提高车辆在避撞响应时的安全性与舒适性。通过仿真验证了该控制算法的可行性。
1 前言
随着汽车保有量的持续增长,交通事故频繁发生,尤其是汽车追尾已占整个交通事故的75%以上[1],追尾碰撞事故造成的损失占整个交通事故损失的绝大部分[2~4]。
为提高车辆行驶的安全性,Yongsoon Yoon等人[5]提出基于模型预测控制方法,结合传感技术与数据融合技术对车辆轨迹进行优化与生成,能有效探测前方障碍并实现避撞;Bageshwar V L等人[6]将避撞控制策略与车辆加速等约束整合到控制算法中对车辆进行控制,提高了稳定性与安全性;Fawaz A等人[7]利用车车通信(V2V)来获取换道时周围车辆的行驶数据,并以此建立避撞模型来控制车辆,实现车辆在换道时的紧急避撞;Caruntu C F等人[8]基于MPC方法,同时考虑通信时间延迟,运用柔性控制李亚普洛夫方程提高了控制输入的稳定性,从而保证了控制系统具有较好的性能;Zhao Jin等人[9]提出一种安全间距策略(SSP),通过获取运动状态和制动能力信息来调节被控车辆的速度和位置,提高了车辆在加速和紧急制动时的安全性;Naus G J L 等人[4,5,10]考虑到异构交通特点,利用V2V无线通信传输车间短程行驶状态数据,设计了分布式协同自适应巡航(CACC)控制器,保证了车辆列队稳定性与行驶安全性。
在研究车辆跟随行驶安全时,一般将前车的减速作为车辆跟随的扰动,而后车通过减速或变道对扰动进行避撞响应,这种对前车减速扰动的避撞响应模式是被动的[11~13],当车辆跟随距离较小时,仅依靠后车制动不能可靠地避撞[14];当后车采取紧急制动来避撞时,将产生较大的减速度,而频繁高强度的制动会使轮胎与制动器磨损加剧,舒适性与燃油经济性变差[15]。
本文以控制主车(以下称主车)为研究对象建立车车跟随模型,基于V2V通信提出一种车车主动协同后端防撞控制算法,利用MPC设计紧急避撞条件下的加速度重分配控制策略,使主车在跟随安全间距约束下保持与前车安全跟随行驶的同时能进行追尾碰撞检查,增加了主车在复杂行车环境中的行驶安全性,并通过仿真验证了算法的可行性。
2 车车协同响应避撞
当主车检测到与后车的跟随距离小于安全距离时,主车向后车发送碰撞危险警告,并读取后车车速、后车加速度、与前车的相对距离和相对速度等信息。在车辆行驶安全性与舒适性的系统约束下,判断仅依靠后车制动减速是否能实现可靠避撞,若不能仅依靠后车制动实现可靠避撞,则需主车在满足系统约束的前提下,通过有条件地加速行驶来主动避让后车,替后车分担减速制动压力。此时,主车立即将自己的加速意图、运动状态等信息传输给与之临近的前、后车。后车读取主车的行驶信息后,按系统设计约束进行制动减速避撞;前车读取主车行驶信息后,判断加速后是否会与主车发生碰撞,若有碰撞的可能,则前车将采取与主车类似的避撞策略来响应碰撞。在实时V2V通信下,通过这种控制方法依靠车辆主动响应可以避免追尾碰撞事故的发生。
3 车辆跟随模型
为了反映主车及其相邻两车的加速状态,在安全间距控制策略下建立主车与后车的跟随模型,如图1所示。在控制过程中,由于作动器、传感器等响应时间有延迟,为了有效地补偿系统的时间延迟并及时地获取控制信号,在车辆跟随模型中采用一阶迟滞[16,17],其表达式[18]为:

式中,τ为控制过程中作动器与传感器引起的一阶延迟;ai(t)为主车加速度;ades(t)为后端防撞系统主车期望加速度。

图1 车车协同相邻车辆跟随模型
根据车辆跟随模型,主车与后车的运动学关系为:

式中,xi(t)、xi-1(t)分别为主车和后车在车辆列队中的位置;di_des(t)为车辆后端防撞系统期望车间距;di(t)为主车与后车的实际车间距;Δdi(t)为主车与后车的跟随间距误差;vi(t)、vi-1(t)分别为主车与后车行驶速度;c为相邻车辆在停车时的最小安全距离;T为恒定车头时距。
由式(1)与式(2)可得:
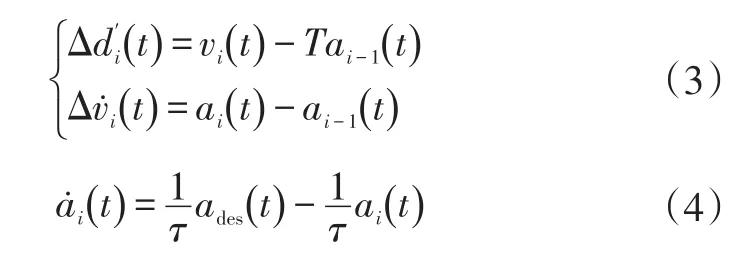
根据式(1)~式(4),将车辆跟随运动学关系表示为状态方程,即

为了对避撞系统进行实时控制,运用零阶保持(Ze⁃ro-Order Hold,ZOH)将车辆跟随模型离散化:

4 后端防撞控制策略
后端防撞系统的主要功能是,在防撞控制策略下通过计算系统动态优化指令来操纵前车,实现对主车的控制,从而达到期望的且安全的车间跟随距离。
4.1 控制系统约束
当主车检测到与后车有碰撞危险时,控制系统开始介入并对主车进行控制,在避免与前后车发生碰撞的前提下最大限度地提高主车的安全性与舒适性。一般地,对舒适性的评价指标主要是加速度变化率,普通乘客能接受的加速度变化率绝对值最大为2 m/s3,超过该值将感觉明显不适,舒适性急剧变坏[19]。故在控制系统中,应对主车加速度ai(t)、主车加速度变化率 ji(t)进行约束与优化。基于此,后端防撞控制系统的约束如下:
a.为了使系统在扰动下能够快速响应并迅速达到稳定状态,在采样k时刻下,系统状态应满足约束:
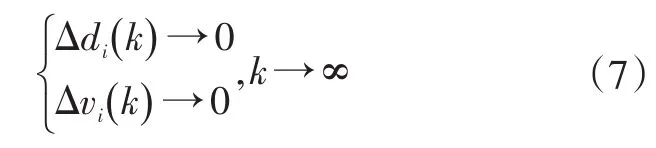
式中,Δdi(k)为主车与后车在采样k时刻的跟随间距误差;Δvi(k)为主车与后车在采样k时刻的跟随速度误差。
b.在防撞系统中,前车将根据车间运动状态进行加速或减速行驶来维持期望车间间距,此时控制系统应对主车的响应进行优化,尽可能地减少或避免主车产生剧烈的加速与减速行为[20],因此,在采样k时刻下,需要根据车辆跟随状态对主车进行运动约束:
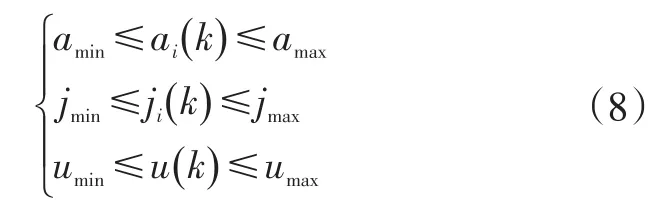
式中,amin、amax为主车加速度在采样k时刻的下界与上界;jmin、jmax为加速度变化率在采样k时刻的下界与上界;u(k)为控制系统输入。
c.在车辆跟随行驶中,为了避免发生后端碰撞,在采样k时刻主车与后车的车间跟随距离d(k)应不小于安全距离,所以控制系统车间距离应满足:

式中,dsafe(k)为在采样k时刻下系统避免后端碰撞的安全阈值。
4.2 车辆列队加速度分配协同策略
车辆在列队行进中,为了对车辆的运动状态进行实时描述,结合式(1)和式(2),引入安全因子λ对车辆列队中主车进行如下数学描述:

式(10)中,若λ≥1,则表明主车与后车无碰撞危险,避撞控制系统此时不介入;若m≤λ<1,则表明主车与后车有碰撞危险,避撞控制系统此时介入,避免碰撞发生;若0<λ<m,则表明极度危险,此时仅通过减速不能避免避撞发生,需进行变道避撞。
由(10)式可知,λ为随相对车间距与行驶时间而变化的常数,m为与车速呈反相关的常数,且m∈(0 ,1)。
当0<λ<m时,纵向的协同加速分配策略不能避免追尾的发生,此时该协同纵向控制不介入,需要进行变道控制规划实现避撞。所以,研究车辆列队在纵向的避撞响应行为时,不考虑0<λ<m时的状况。
当主车检测到与后车有碰撞危险时,需与后车协同响应进行避撞。根据运动学关系,后车在实施减速避撞时,在系统设计约束下,后车的最大期望减速度为:
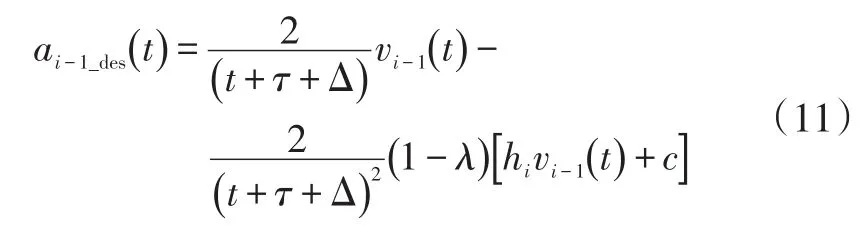
式中,Δ为驾驶员反应时间。
若仅通过后车减速不能避免碰撞,此时需要主车协同加速响应,主动避让后车,即后车将分配一个加速度Δa1(t)给主车,主车将以Δa1(t)进行加速来主动避让后车,达到协同响应避撞的目的。Δa1(t)计算式为:

式中,ai-1_max()t为后车最大制动减速度,由车轮与路面附着系数决定。

式中,μ为车轮与路面附着系数;g为重力加速度。
由式(11)~式(13)得:

则主车以Δa1(t)进行协同加速,同时后车按照ai-1_des(t)进行减速,从而避免与主车发生追尾。但避撞控制系统需要判断通过主车的协同加速是否增加了主车与前车碰撞的危险。所以,由车间跟随安全间距约束有:
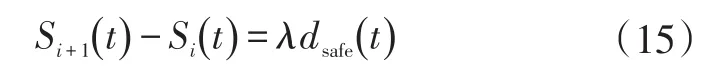
式中,Si(t)为主车Δa1(t)协同加速避让期间行驶的路程;Si+1(t)为主车的前车在相同时间内行驶的路程;dsafe(t)为在t时刻下避撞系统避免发生追尾的车间距安全阀值。
由式(15)可知,当λ≥1时,主车通过与后车协同加速后与前车无追尾碰撞危险,即前车不需要进行协同加速;当0<λ<m时,纵向协同加速控制不介入,需要进行紧急变道避撞;当m≤λ<1时,主车通过协同加速后与前车有碰撞危险,此时需要通过V2V通信,在系统约束下由主车分配一个加速度Δa2(t)给前车,使其协同响应主动避撞。Δa2(t)计算式为:

同理,由式(15)所示的原则可以判断前车通过协同加速后是否与其前车发生追尾碰撞,并做相应的控制决策。
在车辆列队中,当需要有更多车辆参与协同避撞时,第k辆车分配得到的加速度为:
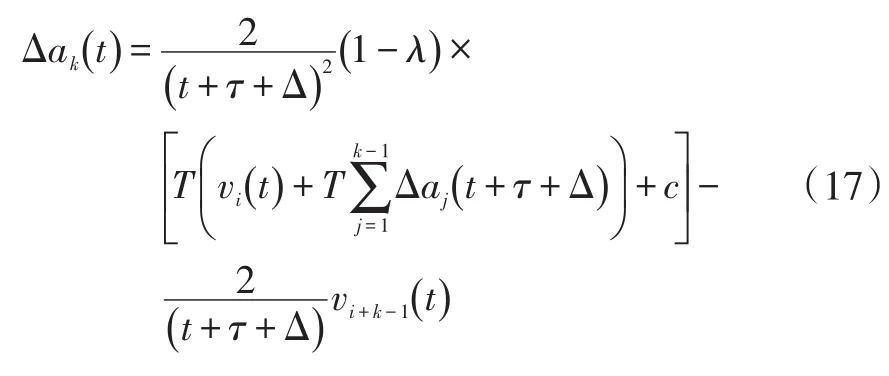
由式(10)~式(17)可知,随着控制系统对避撞的响应,Δdi(t)→0,此时λ→1,根据协同加速策略可知,随着车辆间协同避撞响应的进行,加速度序列Δa1(t),Δa2(t),…,Δak(t)表达式的第1项逐渐减小而第2项逐渐增大,即Δak(t) →0 k=1,2,…,n(n为有限值),故Δak(t)(k=1,2,…,n)序列递减且有下界,为收敛序列。因此,按此加速度分配策略进行协同避撞,车辆列队不会因紧急制动而产生冲击波效应,而是随着车间的协同响应而使扰动迅速衰减。
4.3 控制系统优化求解
后端防撞控制系统主要包括车辆跟随模型、系统约束以及目标函数3部分,如图2所示。

图2 后端防撞控制算法结构
在控制过程中,控制系统参考量R(k+1)为k+1采样时刻下优化的主车期望加速度;后车加速度为系统扰动 ρ(k);控制系统输出为y(k+1)。
根据系统模型与当前状态,采用MPC控制算法对控制系统的未来输出序列Yp(k+1|k)进行预测,并通过求解优化问题来获得当前状态的控制增量序列ΔU(k),再将控制增量序列的第一项作用于系统产生控制行为,然后离散时域向前移动一步,再一次重复优化计算。因此,将车辆跟随模型(6)写成增量方程:
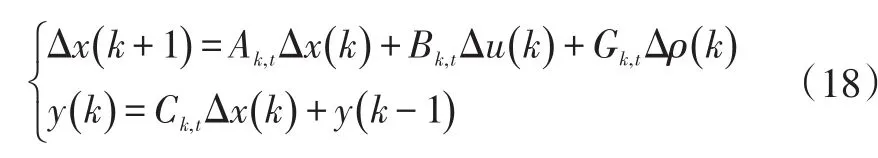
式中,Δx(k) 、Δu(k) 、Δρ(k)分别为系统状态变化量、控制输入变化量以及系统扰动变化量。
在采样时刻k时,系统预测输出序列Yp(k+1|k)和控制增量序列ΔU(k)分别定义为:

式中,Np、Nc分别为系统预测时域与控制时域。
根据增量方程(18),结合yp(k+1|k)与ΔU(k)的定义,可将控制系统的预测输出表示为:

式中,Ψ、I、Φ、Θ为预测系统矩阵。
根据模型预测控制的特点,控制增量序列ΔU(k)在预测时域Np内是未知向量序列,需要设计相应的目标函数来求解在控制时域内满足系统约束的最优控制增量序列。因此,在系统设计约束条件下,设计目标函数J(x(k),ΔU(k))为:

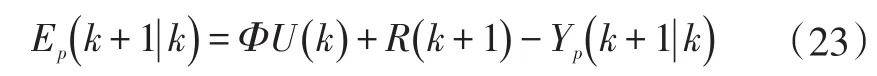
所以,由式(21)与式(23)可得系统的目标函数为:

5 仿真验证
5.1 仿真环境
在MATLAB/Simulink中搭建控制系统模型,基于如下说明进行仿真验证:
a.车辆跟随模型中的两车具有相同的车辆参数,且配备相同的感知测量工具与通信单元,能可靠接收与发送实时运动状态信息;
b.行车条件为良好的无风平直路面,天气状况良好,对无线信号传输无干扰;
c.运用对比方法进行仿真验证,即对加速度未分配和加速度重分配的两种避撞算法进行对比仿真;
d.在未受到后车加速干扰前,主车与后车相距12 m,两车以25 m/s匀速行驶,跟随状态稳定,仿真验证所用参数如表1所列。

表1 仿真采用的参数
5.2 仿真结果分析
为了验证主车在紧急避撞下的响应品质,将后车加速作为跟随扰动,使主车与后车对紧急避撞进行协同响应,在避免碰撞的同时缓解后车的减速制动压力。
在控制系统模型中对跟随后车施加如图3所示的信号作为该系统的扰动信号,即在18 s时使后车以2 m/s2加速行驶2 s后扰动解除,扰动信号解除后主车与后车在协同避撞控制策略下进行协同避撞响应。

图3 控制系统加速度扰动信号
在协同避撞控制中,主车与后车的相对距离响应如图4所示,在受到加速扰动前,两车相距12 m,并保持稳定的行驶状态。在18 s时受到来自后车的加速干扰,从而导致后车与主车的相对距离急剧减小。在22.3 s时,使用加速度未分配的后端防撞控制算法的两车相对距离减小到0,表明此时主车与后车已发生碰撞,且在碰撞发生后的18 s内,两车相对运动状态发生大幅度震荡。使用加速度重分配的后端防撞控制算法的两车相对距离在24.5 s时达到最小值3.8 m,然后再增大并以安全跟车距离稳定行驶,有效避免了碰撞的发生。
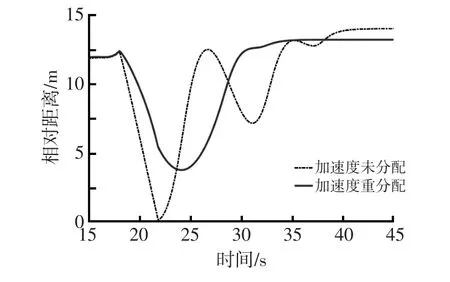
图4 主车与后车的相对距离响应
协同避撞控制下主车的加速度响应如图5所示,两种后端防撞算法均进行加速避撞,使用加速度未分配的防撞控制算法由于只依靠主车进行响应避让,故主车先进行过多加速后再减速,其加、减速度都达到系统设定约束的上、下限值,且产生激烈波动,经历24.5 s后才达到稳定状态。然而,使用加速度重分配的防撞控制算法时,在扰动信号解除(20 s时)后进行协同响应避让,使后车减速制动,同时主车通过加速避让分担了后车的制动压力,其协同避撞响应对缓解制动压力的贡献如图5中阴影面积所示。由于协同响应避让,故主车加、减速度未产生激烈波动,经历16.5 s后达到稳定状态,系统对控制加速度的响应速度改善19.52%。

图5 避撞响应下的主车加速度
协同避撞控制下主车的速度响应如图6所示,当控制系统检测到扰动后,使用加速度未分配的防撞控制算法的主车在检测到系统扰动后,为避免碰撞,速度发生反复波动,在25.5 s时行驶速度达到37 m/s,经历24 s后才达到稳定状态;而使用加速度重分配的防撞控制算法的主车检测到扰动后,开始加速行驶,由于进行协同响应,其行驶速度未发生大幅波动,经历15 s后达到稳定状态,系统对控制速度的响应速度改善23%。

图6 避撞响应下的主车车速
主车加速度变化率在协同避撞控制下的响应如图7所示,在避撞响应过程中,使用加速度未分配的防撞控制算法的主车在进行避让响应时,主车加速度变化率产生很大震荡,其最大绝对值达到5.2 m/s3,超过乘客能接受的最大限制,乘坐舒适性急剧变坏。而使用加速度重分配的防撞控制算法的主车在进行协同避让响应时,主车加速度变化率波动较小,能迅速达到稳定状态,且最大绝对值为1.96 m/s3(<2 m/s3),乘坐舒适性较好,在乘客可接受的范围内。
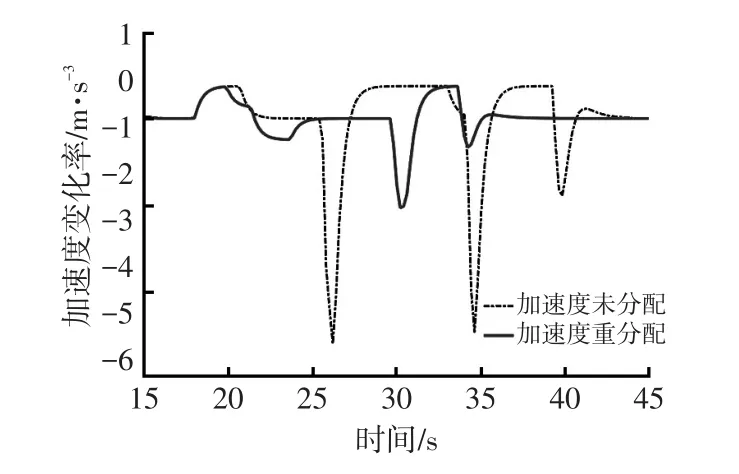
图7 避撞响应下的主车加速度变化率
6 结束语
为研究在车车通信环境下车辆的行驶安全性,设计了一种基于MPC在线优化的加速度重分配后端防撞控制策略,该控制策略可通过车间信息交互使相邻车辆间进行协同响应,避免碰撞的发生。该控制策略不仅能缓解车辆在减速避撞时的制动压力,还能进一步减弱车辆列队中因为紧急制动而产生的速度变动冲击波效应,提高车辆列队行驶稳定性。通过仿真验证表明,所采用的控制策略能有效提高车辆的行驶安全性与乘坐舒适性,同时还具有较好的稳定性与响应品质。
1 董红召,陈炜烽,郭明飞,等.基于车路一体化的车辆主动避撞系统关键技术的研究.汽车工程,2010,32(11):984~988.
2 Schrank D,Eisele B,Lomax T.TTI’s 2012 urban mobility report.in Proc.Annu.Urban Mobility Rep.Texas A&M Transp.Inst.College Station,TX,USA,2012,pp.1~64.
3 Dey K C,Mishra A,Chowdhury M.Potential of intelligent transportation systems in mitigating adverse weather im⁃pacts on road mobility:A review.IEEE Trans.Intell.Transp.Syst.,vol.16,no.3,pp.1107–1119,Jun.2015.
4 Ma Y,Chowdhury M,Sadek A,et al.Integrated traffic and communication performance evaluation of an intelligent ve⁃hicle infrastructure integration(VII)system for online trav⁃el-time prediction.IEEE Trans.Intell.Transp.Syst.,vol.13,no.3,pp.1369–1382,Sep.2012.
5 Yoon Y,Shin J,Kim H J,et al.Model-predictive active steering and obstacle avoidance for autonomous ground vehi⁃cles.Control Engineering Practice,2009,17(7):741~750.
6 Bageshwar V L,Garrard W L,Rajamani R.Model Predic⁃tive Control of Transitional Maneuvers for Adaptive Cruise Control Vehicles.IEEE Transactions on Vehicular Technol⁃ogy,2004,53(5):1573~1585.
7 Fawaz A,Artail H.Enhanced cooperative collision avoid⁃ance in sudden vehicle braking scenarios//Telecommunica⁃tions(ICT),2010 IEEE 17th International Conference on.IEEE,2010:806~813.
8 Caruntu C F.Networked Predictive Cruise Control for Road Vehicles.International Conference on Control Systems and Computer Science.2013:203~209.
9 Zhao Jin,Oya M,Kamel A E.A safety spacing policy and its impact on highway traffic flow.Proc.IEEE Intell.vehicles Symp,2009:960~965.
10 C Design and Experimental Validation:A Frequency-Do⁃main Approach.IEEE Transactions on Vehicular Technolo⁃gy,2010,59(9):4268~4279.
11 庞迪.基于变结构滑模控制理论的汽车操纵稳定性控制策略研究:[学位论文].重庆:重庆大学,2005.
12 崔崇桢.多种典型工况下的汽车正面碰撞性能协同优化:[学位论文].长沙:湖南大学,2014.
13 Luo Lihua,Liu Hong,Li Ping,et al.Model predictive con⁃trol for adaptive cruise control with multi-objectives:com⁃fort,fuel-economy,safety and car-following.Journal of Zhejiang University-Science A(Applied Physics&Engi⁃neering),2010,11(3):191~201.
14 Sancar F E,Fidan B,Huissoon J P,et al.MPC based col⁃laborative adaptive cruise control with rear end collision avoidance.Intelligent Vehicles Symposium Proceedings.IEEE,2014:516~521.
15 刘筠,王剑华.加速度变化率对汽车制动器磨损特性的影响.长安大学学报(自然科学版),2007,27(6):95~98.
16 瞿宏敏,程军.汽车动力学模拟中的轮胎模型述评.汽车技术,1996(7):1~8.
17 Rajamani R,Choi S B,Law B K,et al.Design and experi⁃mental implementation of longitudinal control for a platoon of automated vehicles.Journal of dynamic systems,mea⁃surement,and control,2000,122(3):470~476.
18 Bageshwar V L,Garrard W L,Rajamani R.Model Predic⁃tive Control of Transitional Maneuvers for Adaptive Cruise Control Vehicles.IEEE Transactions on Vehicular Technol⁃ogy,2004,53(5):1573~1585.
19 Martinez J J,Canudas-De-Wit C.A Safe Longitudinal Control for Adaptive Cruise Control and Stop-and-Go Sce⁃narios.IEEE Transactions on Control Systems Technology,2007,15(2):246~258.
20 Kianfar R,Augusto B,Ebadighajari A,et al.Design and Experimental Validation of a Cooperative Driving System in the Grand Cooperative Driving Challenge.IEEE Trans⁃actions on Intelligent Transportation Systems,2012,13(3):994~1007.
(责任编辑 文 楫)
修改稿收到日期为2017年3月10日。
Research on Cooperative Active Rear-End Collision Avoidance Based on MPC
Yu Guokuan,He Feng,Zhao Jin
(Guizhou University,Guiyang 550025)
In order to improve the active safety of vehicles in complex driving environment,a novel rear-end collision avoidance algorithm was proposed to distribute the braking deceleration based on MPC(Model Predictive Control)on-line optimization,which made the adjacent vehicles respond cooperatively through information exchange braking deceleration between vehicles,to avoid collision.The results show that the braking pressure is alleviated by inter-vehicular cooperatively responding,which improves the driving safety and ride comfort of vehicle in the process of collision avoidance response.Simulation verifies feasibility of this control algorithm.
V2V cooperative,Rear-end collision avoidance,Acceleration redistribution
车车协同 后端防撞 加速度重分配
U461.91 文献标识码:A 文章编号:1000-3703(2017)08-0012-07
国家自然科学基金(61164007)和贵州大学研究生创新基金(研理工2016028)项目资助。
