借助数学模型突破截交线与相贯线的教学难点
2017-09-11王志军
王志军
(江苏省张家港工贸职业高级中学,江苏 张家港 215600)
借助数学模型突破截交线与相贯线的教学难点
王志军
(江苏省张家港工贸职业高级中学,江苏 张家港 215600)
为适应数控自动化机械操作的需要,改革传统机械制图教材;增加截交线、相贯线及其展开方程的介绍;力求提高学生的操作技能。
机械制图;截交线;相贯线;方程;教学改革
1 问题的提出
在职业学校现行的《机械制图》教材中,关于截交线与相贯线内容的教学,主要是基于传统的机械加工方法,包括放样制作、划线、手工切割等组织教学。在生产实践中,由于受这种手工作图与手工操作局限性的限制,在质量、效率上都难于达到高水准。
随着科技的发展,企业转型升级的需要,机械自动化程度的不断提高,这种传统的方法已经被数控技术、甚至机器人技术所逐步取代。基于上述原因,职业学校的《机械制图》教学为了适应这一需求,势必要对这些呈现滞后性的教学内容实施改革。
2 解决方案
笔者认为,可以在《机械制图》课程适当增加有关截交线与相贯线的数学模型构建的介绍,掌握数控编程中所需的有关轨迹方程的求解,选取适当的应用实例给学生实习。文章举几个例子进行说明:
(1)圆柱体正截面交线及其展开线的方程。首先给出圆柱体正截交线是椭圆的理论证明,让学生从理性上加深截交线是椭圆的认识,并掌握圆柱圆半径r、截面与圆柱底面倾斜角α、椭圆长半轴a、短半轴b等元素间的关系,利于实际相关问题的计算与处理等。
圆柱体正截交线是椭圆的证明:如图1所示,设圆柱体底面半径为r。在圆柱体斜截面上方放置一个半径为r,与圆柱体内壁和斜截面都相切的球,它与斜截面产生了一个切点F1;在圆柱体斜截面下方也放一个半径为r,与圆柱体内壁和斜截面都相切的球,它与斜截面产生了另一个切点F2。由于球外一点到球的各方向切线都相等,因此,斜截面边界上的所有点P到斜截面上的两个切点距离和PF1+PF2总是等于这个点到上下两圆与圆柱体内壁相切处的距离和PM+PN=O1O2=定值(即上下两圆的圆心距离),也就是说,根据椭圆定义:一个支点到两个定点的距离的和是定值,则这个动点的轨迹是椭圆,所以,这个斜截面是以两切点为焦点的椭圆。

图1

图2
探索截面椭圆、倾角、底圆半径等元素间的关系:如图2所示,设截面椭圆与圆柱底平面的交角为α,则椭圆短轴2b=2r为定值,椭圆长轴2a方向与交角方向一致,a、b、r、α等之间的关系为b=r=aCosα。于是,在正截面上的椭圆方程为借助上述关系,可知O'A在侧面的射影等于O'C=AC·tgα。得到截面左视图随倾角α变化的变化规律:α=45°,截面左视图是圆;α>45°,截面左视图是长轴为O'A射影的椭圆;反之亦然。
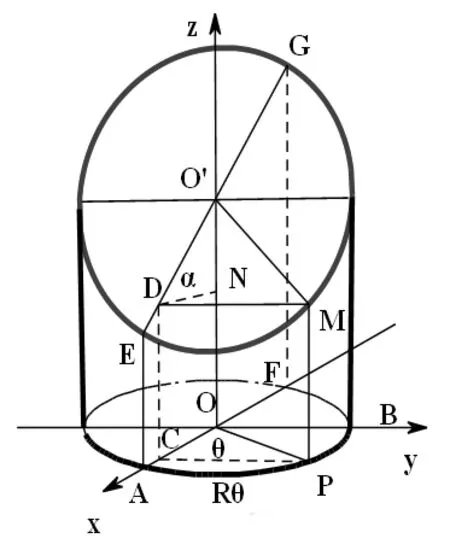
图3
圆柱体正截交线平面展开图形轨迹的探求。关键是要掌握其椭圆在空间的轨迹方程,如图3所示,设圆柱体半径为R;斜截面与柱体底平面(垂直于中心轴的截面)夹角为α;斜面中心到底平面距离为h。根据对称性,设定展开时沿FG剪开铺平,若以A为坐标原点,AE为y轴,那么圆周就是展开图的x轴。截面圆周上动点M,在展开图上横坐标就是AP“弧”(有正负),纵坐标就是高PM。以AP“弧”(有向)的圆心角θ(-π≤θ≤π)为参数,则x=Rθ,y=PM=CD=ON=OO‘-N O’=h-DN*tanα=h-OC*tanα=h-Rcosθtanα。消去参数θ,得到y=h-(Rtanα)cos(x/R),-πR≤x≤πR。
取h=3,R=2,α=30°,可以非常轻松的作出其平面展开图,效果如图4所示。

图4 平面展开效果图
(2)两圆柱面相贯线及其展开曲线的方程。设圆柱体Ⅰ和Ⅱ的半径分别为R和r(R>r),两异面轴线成角θ,距离为e。建立如图5所示的坐标系,yoz平面向前移动e,再逆时针转θ,则与y'o'z'平面重合;于是,根据旋转公式与平移公式有:


图5
Ⅱ圆柱面在o'-x'y'z'中的参数方程为:

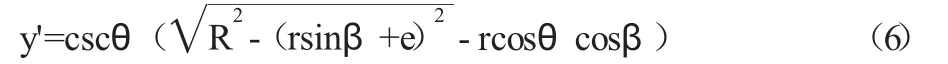
则有两圆柱面相贯线在坐标系o'-x'y'z'中的参数方程为:
β=0~2π,是参数方程的参数。
将式(4)代入式(5)整理得:
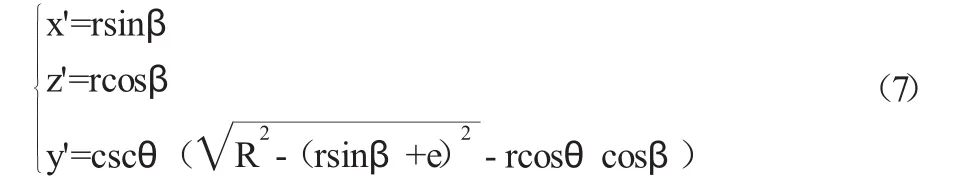
对圆柱体Ⅱ,从其在o'-x'y'平面母线处展开为平面,则两圆柱面相贯线在展开的新平面内的曲线方程的纵坐标f(x)=y',横坐标x的值是半径r圆的圆心角β所对的圆弧长l,即x=l=rβ。
设R=3.5、r=1、θ=30°、e=1,则其展开曲线的平面图图图6所示。

图6
对于圆柱体I、II的情形,当轴线选取不同的坐标轴时,所得到的相贯线参数方程的形式略有不同,但结构的本质是一致的。运用类似的方法,可得各类立体面的相贯线方程及其平面展开线方程,由于篇幅关系,这里就不再具体展开。
(3)应用举例。在生产实际中,经常会遇到一些截交和相贯的问题,例如拉杆接头上的截交线(如图7(a)所示)和三通上的相贯线(如图7(b)所示),因此必须研究求作截交线和相贯线的一般方法。
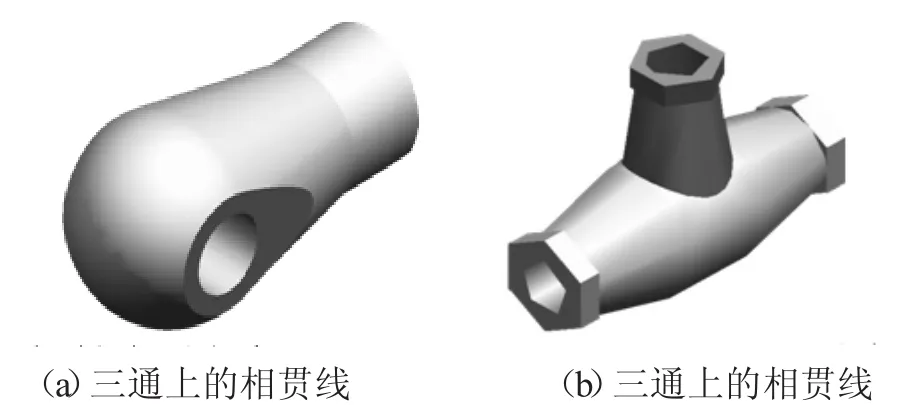
图7
首先分析该立体是由哪些基本体所组成的,接下来分析截平面与每个被截的基本体的相对位置、截交线的形状和投影特征,最后可以逐一画出基本体的截交线,围成封闭的平面图形。
该组合体(拉杆接头)由同轴的圆柱、圆锥和圆球三部分构成。头部被正平面P前、后对称地各切去一块,在前、后表面上各产生一条封闭的平面曲线。从俯视图中可以看出,截平面P和圆柱不相交,P平面和圆球的截交线是圆,P平面和圆锥的截交线为双曲线。由于截平面为正平面,所以截交线的 V面投影反映其实形,H面、W面投影积聚成直线段。
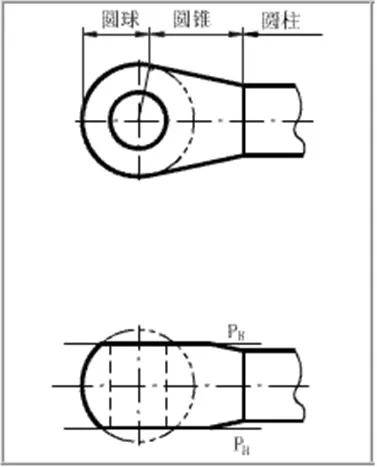
图8
作图:(如图8所示)找到圆球与圆锥的分界线,然后分别求出这两段截交线,两段截交线的结合点必在分界线上,然后找到双曲线的特殊点(顶点)并利用双曲线的相关知识去解决一系列问题。
3 结论
文章给出的截交线、相贯线数学模型的构建过程,为处理同类问题,提供了一种有效的思维方法,为机械专业类学生在数控车床、数控焊接机器人的操作应用上,提供了必要的知识贮备,提升了实际操作能力,为实施课程改革,构建现代化职教课程体系,增添了无限活力。
Using M athematical M odel to Break the Teaching Difficulty of Interception Line and Intersection Line
WANG Zhi-jun
(Zhangjiagang Industry and Trade Vocational High School,Jiangsu Province,Zhangjiagang,Jiangsu 215600,China)
In order to meet the needs of CNC automatic mechanical operation,it needs to reform the traditional mechanical drawing materials,add intersecting lines and extended equation and improve the operational skills of students.
mechanical drawing;intersecting line;equation;teaching reform
TH126-4
A
2095-980X(2017)06-0167-02
2017-05-15
王志军(1970-),男,江苏张家港人,大学本科,高级讲师,主要研究方向:机械工程教育。
