基于量子遗传的蒙特卡洛节点定位算法
2017-09-11田浩杉
田浩杉
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
基于量子遗传的蒙特卡洛节点定位算法
田浩杉
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
针对无线传感器网络(WSNs)节点定位的问题,提出了一种量子遗传算法与蒙特—卡洛相结合的定位算法(QGA-MCL)。将QGA应用于MCL中的采样过滤阶段,通过合理的编码方案、译码方案以及量子旋转门对采样区域中随机产生的量子染色体进行操作,提高了样本寻优效率和定位精度,并加快了算法的收敛速度。仿真结果表明:与蒙特—卡洛定位算法相比,提出的QGA-MCL算法能够减少约10.2 %的定位误差,同时,算法的收敛速度也得到了显著提升。
无线传感器网络; 量子遗传算法; 蒙特—卡洛定位算法
0 引 言
早在2004年,蒙特—卡洛定位(Monte-Carlo localization,MCL)算法便由机器人定位中引入到了移动无线传感器网络[1~6](wireless sensor networks,WSNs)中进行节点定位,虽然MCL定位算法抛开了节点移动性的干扰,甚至节点移动速度越大定位精度越高,但采样成功率很低,并且容易出现粒子退化的问题[7]。近年来,很多学者对其进行了改进,文献[8]提出了蒙特-卡洛盒子定位(Monte-Carlo location boxed,MCB)算法,通过锚箱(anchor box)和采样箱(sample box)缩小采样区域,从而提高了采样效率。但当观测模型分布在锚箱的比重很小时,采样的成功率仍然很低[9,10]。文献[11]提出了动态静态网络节点定位(mobile and static sensor network localization,MSL),算法利用邻居节点中定位精度较高的节点来辅助定位,但其计算过程非常复杂,通信耗能也比较大。文献[12]将DV-Hop引入到了MCL定位中,提出了多跳蒙特—卡洛定位(multi-hop-based Monte-Carlo localization,MMCL)算法,充分利用了锚节点的信息,在低锚节点密度的网络中表现出了良好的定位性能。上述算法从不同角度对MCL算法进行了改进,但在网络拓扑变化比较频繁的高速移动网络环境下,上述算法的稳定性和网络生存性则存在一定的性能缺陷。
本文在MCL定位算法的基础上引入了一种通过量子遗传的方法来提高寻优效率,即QGA-MCL算法,算法通过新的寻优手段将MCL的样本采集及过滤阶段优化,提高了收敛速度和定位精度。
1 MCL基本原理
在WSNs监测区域内随机部署P个目标节点和M个锚节点。目标节点具有以下特征:节点随机运动;每个节点运动模型独立;节点具有相同的属性。下面将重点关注一个目标节点,通过MCL算法来预测该节点位置。算法主要通过预测和过滤2个阶段实现。
在MCL算法中时间被分割成等长的离散时间段,用t={1,2,3,…}表示离散的时间,并且假设仅已知待定位节点的最大移动速度Vmax。待定位节点在每一个时间段内都要重新定位。


(1)
式中 d(lt,lt-1)为节点在t时刻和t-1时刻的欧几里得距离,当节点的最大运动速度Vmax越大时,所对应的采样区域便越大,加大了定位误差。如果加入了节点的运动模型,根据运动模型来缩小采样区域,便会提高采样效率,减小定位误差。传统MCL算法的采样区域如图1所示。
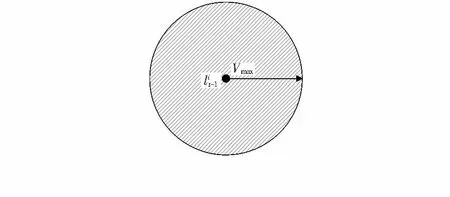
图1 传统MCL采样区域
2)过滤阶段:根据节点在t时刻接收的由一跳邻居锚节点和二跳邻居锚节点所发送的观测信息对采样点进行筛选,将不符合要求的过滤掉。对于采样点l的过滤条件可表示为

(2)
式中 S为目标节点周围的一跳锚节点;T为其周围的二跳锚节点;r为锚节点的通信半径;l为采样粒子;s为锚节点。符合约束条件的采样区域如图2、图3所示。

图2 一跳和二跳锚节点约束区域
经过一次过滤后剩余的有效采样点数量不足以达到定位条件,便需在采样区域内进行重新采集并重复过滤过程,直到有效样本数达到设定数目为止。
MCL算法虽然在一定程度上解决了粒子在运动状态下的定位问题,但由于该算法的样本在采样区域内随机产生,导致采样效率不高,采样的成功率很低。随着迭代次数的增加,粒子退化现象变得严重。基于此,本文通过新的采样手段实现快速有效地寻找样本的最优解。
2 基于量子遗传算法的MCL节点定位
2.1 量子遗传算法
量子遗传算法(quantumgeneticalgorithm,QGA)[13]不仅增加了粒子的多样性,防止粒子退化现象出现,同时,有效缩短了计算时间且改善粒子定位能力[14]。QGA没有采用传统遗传算法的选择、交叉、变异等操作方法,而是构造量子旋转门作用于量子叠加态,使其相互干扰,改变旋转角度,更新种群,从而可以通过量子旋转门来实现对染色体的操作[15]。
2.2 量子比特
量子计算中采用了|0〉和|1〉表示微观粒子的两种基本状态,将其称为量子比特(qubit)。处于两种基本状态的线性组合状态称之为叠加态,表示为
|φ〉=α|0〉+β|1〉,|α|2+|β|2=1
(3)
式中 α,β为一对复数,称为量子态的概率幅;|α|2和|β|2分别为量子态中2个基本态的选择概率。因而,量子最终处于何种状态由2个概率幅决定,可以简化表示为
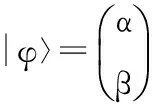
(4)
2.3 QGA-MCL实现步骤
1)随机产生一个M+P个节点的网络拓扑图,并对其进行初始化和预处理(M个锚节点,P个目标节点)。
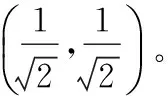
3)对该P条量子染色体依据编码方案进行编码操作。

5)以p0为目标,用量子旋转门对种群中量子染色体予以更新,更新时根据方向准则变换,大小为10e-t/maxt(t为代数)。

7)在遗传过程中,判断种群是否需要变异。若连续数代最优个体均无任何变化且未达到适应度阈值时,便对种群进行变异操作,采用量子非门手段。
8)返回步骤(4),循环计算,直到满足结束条件(最优个体的适应度达到给定阈值或达到预定的迭代次数)。
9)输出最优解。
2.4 QGA-MCL算法具体描述
2.4.1 编码阶段
对于每一个随机采集的样本点(xj,yj),用量子染色体呈现。由于考虑的是二维空间,需要通过2个量子位表示染色体,因此,本文直接用量子位的概率幅进行编码。
在初始化阶段,样本点偏向x轴和y轴的概率相同。所有P条染色体的概率幅为

(5)
进入编码阶段,编码方案如下
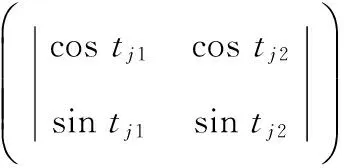
(6)
式中tj1,2=2π×rnd,rnd为(0,1)间的随机数;P为采样点个数。
2.4.2 解码阶段
通过MCL阶段所确定的采样区域为
(7)
则在解码阶段有如下的线性关系

(8)
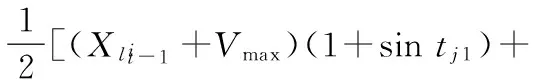
(9)
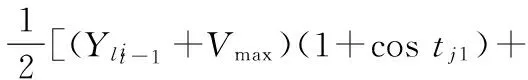
(10)

(11)
通过解码手段对每条随机产生的量子染色体进行x轴分量与y轴分量的转换。
2.4.3 适应度函数的选取
按照适应度函数的设计原则,在QGA搜索求解过程中,常常求解最小值。针对平均误差值的研究,假设di为根据测距手段测量出的目标节点与锚节点i之间的距离,为已知量,采样区域内所有采样点的坐标为(xj,yj);锚节点的坐标为(xi,yi)。适应度函数值最小的为当代染色体的最优解
fitnessj(xj,yj)=
(12)
2.4.4 种群更新
种群更新的目的是使所有随机产生的染色体向当代最优染色体靠拢。对于QGA,种群的更新可以通过量子旋转门对染色体进行操作实现。常用的量子旋转门为

(13)
由此对种群进行更新
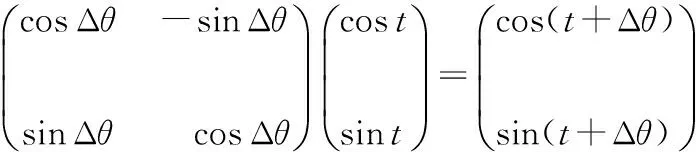
(14)
旋转门的转角大小和方向可以改变,与此同时,其也影响着算法的收敛速度。
1)转角方向
(15)
式中α0,β0为当前全局最优染色体上量子位的概率幅;α1,β1为当前代某染色体上相应量子位的概率幅,则转角θ的方向选取规则为:当A≠0 时,方向为-sgn(A);当A=0时,方向取正负均可。
2)转角大小
Δθ=10e-t/maxt
(16)
式中t为遗传代数。一般转角的大小可选取0.001π~0.05π。
3 仿真实验

(17)
图3描述了在监测区域内,各个锚节点和目标节点在某一时刻的位置信息。各个目标节点在监测区域内相互独立并以[0,Vmax]的速度随机运动。

图3 节点分布
3.1 定位误差对比
实验设定测距误差为20 %,连通度为5,共测得120个数据,仿真结果如图4所示。从仿真结果可看出:QGA-MCL算法的定位误差比传统MCL算法要小。具体为:QGA-MCL的平均定位误差约为17.5 %,其最大定位误差比最小定位误差高约8.7 % ;MCL算法的平均定位误差约为27.74 %,其最大定位误差比最小定位误差高约15 %;QGA-MCL比传统MCL的平均定位误差降低了约10.24 %。由此得出:QGA-MCL算法的定位精度和稳定性比MCL算法高。

图4 定位误差对比
3.2 锚节点密度与算法收敛速度的关系
如图5所示,在不同锚节点密度的情况下,各类MCL算法的收敛速度均会有所提高,为使最终解的适应度值达到所设定的阈值,QGA-MCL算法在相同锚节点密度的情况下明显较传统MCL算法的搜索速度快,在很大程度上提高了算法效率,避免了传统MCL算法中对相同粒子的重复操作。
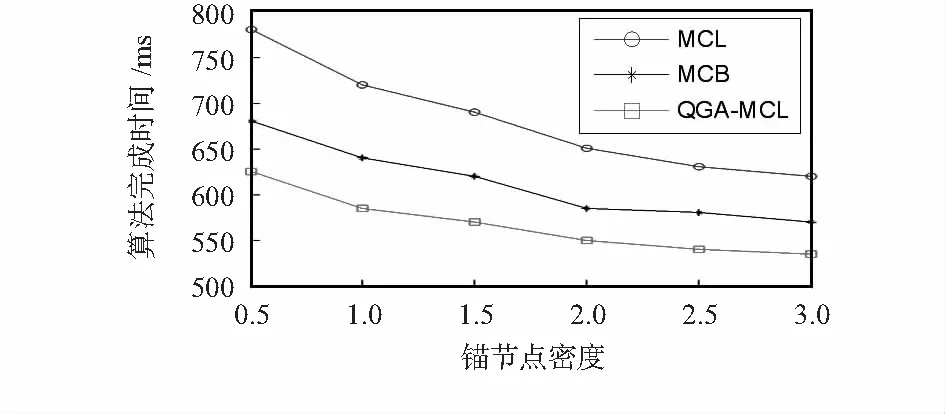
图5 锚节点密度对定位误差的影响
3.3 节点最大速度Vmax与平均定位误差的关系
图6为随着目标节点Vmax的变化,不同类型MCL算法平均定位误差的变化曲线。从图中可看出:随着Vmax的增大,各类MCL算法的平均定位误差之间的差异逐渐缩小。最大速度在定位过程中的2个阶段影响定位精度:1)预测阶段,采样区域与节点的最大速度有关,随着Vmax加大将导致采样样本的准确度下降。最大速度对基于MCL的所有算法的影响均相同。2)每个时间段,节点的平均速度越大,目标节点能够接收到的观测信息就越多[13],进而滤除更多不符合条件的样本。QGA-MCL算法的采样阶段是在采样区域中随机产生量子染色体,对染色体进行迭代寻优的过程。所以,目标节点的速度越大,观测到的关于采样区的信息就越多。

图6 最大速度对定位误差的影响
4 结束语
在MCL算法的基础上,引入了QGA进行粒子快速寻优,提出了QPS-MCL算法,虽然在染色体编码译码时由于计算量消耗了较多能量,但在很大程度上,提高了算法效率,避免了复杂的样本采集和过滤。通过仿真实验证明:相比于MCL和MCB,算法在不同锚节点密度和运动速度下有着良好的定位性能,定位精度有所提高。
[1] Shi H,Wang W.Game theory for wireless sensor networks:A survey[J].Sensors,2012,12(7):9055-9097.
[2] 张 品,毛文敏,徐 静.一种基于迭代投票的无线传感器网络安全定位算法[J].传感器与微系统,2015,34(12):118-120.
[3] Yusuke Wada,Takamasa Higuchi,Hirozumi Yamaguchi,et al.Accurate positioning of mobile phones in a crowd using laser range scanners[C]∥2013 IEEE 9th International Conference on Wireless and Mobile Computing,2013:430-435.
[4] ZeKavat Buehrer.Handbook of position location: Theory,practice and advance[M].Hobker:John Wiley & Sons,2012: 359-395.
[5] 邓成玉,王宇峥,谷晓英,等.基于细菌觅食算法和跳段校正的无线传感器网络定位算法[J].燕山大学学报,2014,38(6):544-555.
[6] 金 纯,王升刚,尹远阳.WSNs中一种基于移动新标检测的定位算法[J].传感器与微系统,2014,33(2):142-145.
[7] 刘小康,张 翔,方 爽.基于ZigBee无线传感器网络的一种室内定位新方法[J].传感器与微系统,2013,32(11):29-32.
[8] Baggio A,Langendoen K.Monte Carlo localization for wireless sensor networks[C]∥Proc of 2nd Int'l Conf on Mobile Ad Hoc and Sensor Networks,MSNs 2006,Hong Kong,Springer Verlag,2006:718-733.
[9] 刘志华,李改燕,刘晓爽.基于最小二乘法的蒙特卡洛移动节点定位算法[J].传感技术学报,2012,25(4):541-544.
[10] 王曙光.无线传感器网络的分区域质心定位算法[J].传感器与微系统,2014,33(12):149-151.
[11] Rudafshani M,Datta S.Localization in wireless sensor net-works[C]∥Proceedings of the 6th International Symposium on Information Processing in Sensor Networks,Cambridge,MA,USA,2007:51-60.
[12] Yi Jiyong,Won Yangsung,Cha Hojung.Multi-hop-based Monte Carlo localization for mobile sensor networks[C]∥Proceedings of The 4th Annual IEEE Communications Society Conference on Sensor,Mesh and Ad Hoc Communications and Networks,San Diego,California,USA,2007:163-171.
[13] 杨 娟,韩雪松.基于遗传算法优化的节点定位技术[J].制造业自动化,2015,37(2):95-97.
[14] 董跃钧,李国伟.量子遗传优化粒子滤波的WSNs目标跟踪算法[J].科学技术与工程,2013,13(12):3305-3309.
[15] 刘 宏,王齐涛,夏未君.基于量子遗传算法的WSNs三维定位方法[J].广西师范大学学报,2015,33(4):49-54.
Monte Carlo node localization algorithm based on quantum genetic
TIAN Hao-sha
(School of Electronic and Information Engineering,Lanzhou Jiao Tong University,Lanzhou 730070,China)
A new node localization algorithm is proposed for wireless sensor networks(WSNs),which combines quantum genetic algorithm with the Monte Carlo localization(QGA-MCL).QGA is applied to the sampling filtering stage in MCL.Operate the quantum chromosomes which is random generated in sampling area by reasonable encoding scheme,decoding scheme and quantum rotating gate.Simulation results demonstrate that compared with Monte Carlo localization algorithm,the proposed QGA-MCL algorithm can reduce positioning error about 10.2 %,and meanwhile,the convergence speed of algorithm is improved significantly.
wireless sensor networks(WSNs); quantum genetic algorithm(QGA); Monte Carlo localization(MCL)algorithm
10.13873/J.1000—9787(2017)09—0125—04
2016—09—09
TP 393
A
1000—9787(2017)09—0125—04
田浩杉(1992-),男,硕士,主要研究方向为无线传感器网络节点定位技术。
