如此称重准确吗

陈小磊

(江苏省泰州中学 江苏 泰州 225300)

如此称重准确吗

陈小磊

(江苏省泰州中学 江苏 泰州 225300)

通过对“双秤砣”法称重的准确性进行分析，将力矩平衡问题与实际生活应用联系起来．

力矩平衡 双秤砣 称重

1 问题引入

有一水果店，所用的秤是吊盘式杆秤，量程为10 kg．现有一较大的西瓜，超过此秤的量程，为得到其质量，店员找来与原秤砣完全相同的另一秤砣，并提出采取“双秤砣法”称量，即把此秤砣与原秤砣结成一起作为秤砣进行称量．平衡时，双砣位于刻度6.5 kg处，他将此读数乘以2得13 kg作为西瓜的质

表1 两个阶段的物理量

从表1中的计算结果可以看出：物体下滑的第一阶段，动能增加ΔEk1=25 J，产生热量Q1=10 J，重力势能减少15 J，物体减少重力势能可以让传送带少提供一部分能量，根据能量守恒，传送带由于运送物体需多消耗能量

E1=ΔEk1+ΔEp1+Q1=20 J

对传送带分析可以证明这一点，传送带克服摩擦力做功

即满足

E1=W1

物体下滑的第二阶段，该过程物体动能增加ΔEk2=11 J，产生热量Q2=2 J，重力势能减少33 J，根据能量守恒，物体减少的重力势能转化为动能和热量，还剩下20 J的能量，这20 J的能量可以帮助传送带克服转轴等处的阻力做功，电动机可以少输出20 J的能量，即传送带由于运送物体需多消耗能量

E2=ΔEk2+ΔEp2+Q2=-20 J

对传送带分析，滑动摩擦力对传送带做正功

相当于传送带“克服”摩擦力做功-20 J，传送带保持速度始终恒定，动能保持不变，电动机运送物体不需要多消耗能量，反而少消耗20 J的能量，传送带的输出功率P0必然减小．

全过程来看，动能改变ΔEk=36 J，产生热量

Q=12 J，重力势能减少48 J，传送带由于运送物体需多消耗能量

E=ΔEk+ΔEp+Q=0

即第一阶段电动机多输出20 J，第二阶段少输出20 J，总体来看，送带运送物体不需要多消耗能量．全程摩擦力对传送带做功W为零，可以得到E=W，即物体、传送带整个系统的总能量是守恒的．

传送带问题的一系列特点都是由传送带和被传送的物体之间的摩擦力做功等特点决定的．在忽略空载到重载运行过程的理想化模型下进行分析，传送带运送物体多消耗能量

E=ΔEk+ΔEp+Q

等于传送带因运送物体克服摩擦力所做的功．如果摩擦力对传送带做正功，传送带不会出现“被加速”，而是传送带的电动机将降低功率P0，少输出能量，来维持自身恒定的速度，物体、传送带整个系统的总能量仍然守恒的．

量卖给顾客．试问：店员所称西瓜的质量准确吗？

2 思路分析

杆秤问题是典型的固定转动轴物体的平衡问题，主要通过力矩平衡求解，即以提纽为转轴，所称物体重力、杆秤重力、秤砣重力，这3力的力矩平衡．

如图1所示，设杆秤的提纽C与秤盘的悬挂点A的距离为d，零刻度O到C点的距离为l0，杆秤的刻度是均匀的，每千克刻度长为λ，秤砣质量为m0，秤杆(含秤盘)重力为G0，其重心与O必在C点两侧．当秤盘中不放物体时，秤砣置于O点，杆秤平衡，以C为转轴，则秤杆(含秤盘)重力的力矩MG0与秤砣重力的力矩平衡，即

MG0=m0gl0

(1)

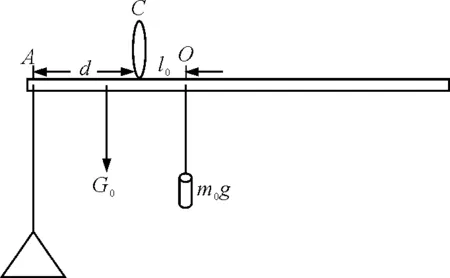
图1 吊盘式杆秤

当秤盘中放上质量为m(kg)的物体时，秤砣应右移λm达平衡(图2)，即

mgd+MG0=m0g(l0+λm)

(2)

由式(1)、(2)可得

d=λm0

(3)

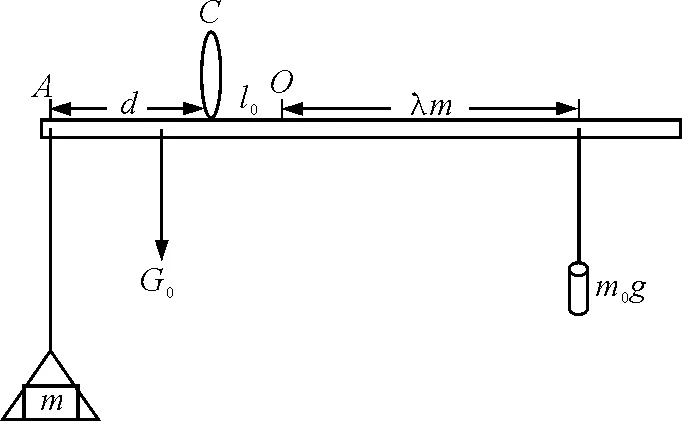
图2 杆秤称物

当用双秤砣称量质量为m的物体时，设读数为m′(图3)，平衡时应有

mgd+MG0=2m0g(l0+λm′)

(4)

由式(1)、(3)、(4)可得

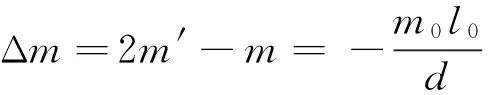
图3 用双秤砣称物

因此得出以下几点：

(1)按照图1，2，3所示杆秤，“双秤砣法”称量的质量偏小；

(2)若秤杆(含秤盘)重心位于提纽右侧(如图4)，零刻度线O位于提纽左侧，则l0<0，“双秤砣法”称量的质量偏大；

(3)若秤杆(含秤盘)重心与零刻度线重合于C处，则l0=0，“双秤砣法”称量的质量准确无误.

图4 秤杆重心位于提纽右侧

3 反思拓展

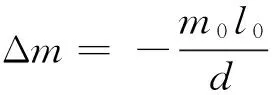
1 程稼夫.中学奥林匹克竞赛物理教程(力学篇).合肥：中国科技大学出版社，2002.12

2 范小辉.新编高中物理奥赛指导.南京：南京师范大学出版社,2012.9

2016-12-23)