中学物理与中段反导
2017-09-11吴迪青
吴迪青
(余姚市第四中学 浙江 余姚 315400)
中学物理与中段反导
吴迪青
(余姚市第四中学 浙江 余姚 315400)
中学物理中在讲万有引力与圆周运动时,如何讲“萨德”与“反导”成了许多教师的一个难题,有的都不敢提反导,因为一套高深的弹道理论成了不可逾越的障碍,但利用Excel的计算和描图功能,另辟蹊径,成功解决这个难题,通过弹道轨道和拦截轨道的计算和模拟,使得原来的不可能变为可能,并且能形象展示弹道轨迹,由此展开了中学物理中用现有知识研究“反导之旅”,以此为引导开展研究性学习,拓展学生视野,激发学生学习物理的兴趣.
反导 弹道导弹 拦截 万有引力 速度
各位读者,你真的没有看错,本文讲述的是以中学物理的知识研究弹道导弹的中段反导,不过要借助于一个常用的工具软件Excel.时下“萨德问题”已对中国的国家安全造成威胁,萨德是美国国家导弹防御计划中的一部分,所以反导成为热点.中国的中段反导已成功试验多次,有资料显示中国的中段反导世界领先,甚至有学者表示现在外星人入侵只有中国有能力对付.每次与学生谈及此事,学生的喜悦之情溢于言表,兴奋不已.但是,限于中学知识的不足,无法做具体的分析和计算,甚是遗憾.今天,我们用Excel的计算和数据处理功能,来突破这一障碍,计算弹道导弹的轨道及反导系统的轨道计算,满足学生的求知欲,激发学生学习物理的热情.
1 中学物理中的弹道导弹轨道计算
1.1 弹道导弹轨道模型
弹道导弹的发射轨道模型,如图1所示.
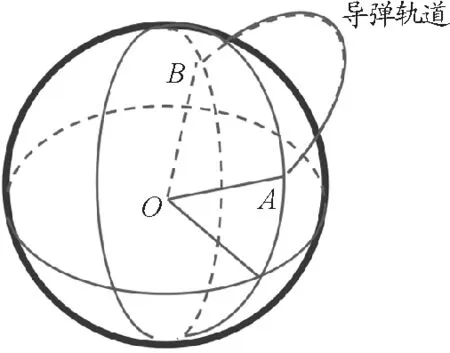
图1 弹道导弹轨道发射模型
弹道导弹从地球的A地发射,命中地球上的B地,弹道导弹飞行的轨道为一椭圆轨道,虽然导弹的初段和末段不是严格的椭圆轨道,但我们今天分析的是中段反导,可以按椭圆轨道来处理,为什么呢?
如图2所示,弹道轨道平面图.
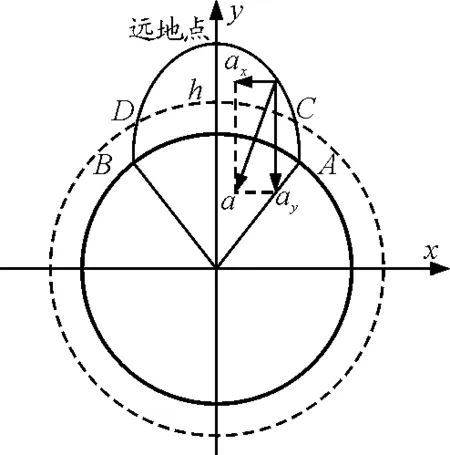
图2 弹道导弹平面图
轨道平面为经过A,B两地及地心的一个平面,虚线为大气层,国际航空联合会定义的大气层和太空的界线,高度为100 km的界线为卡门线,卡门线外为太空,即大气层厚度约100 km[1].导弹飞行的初段为图中的A到C段(C点为出大气层点),由于火箭的助推和大气层的缘故,这段轨道不稳定,加上发射初期雷达的探测盲区,这一段打击难度大,第二段火箭助推结束,导弹飞出大气层,进行惯性飞行阶段,由C经远地点到D段即飞行中段(D点为再入大气层点),这一段轨道比较稳定,但飞行高度高,导弹速度大,也不易打击,中国显然已突破这一难题,我们分析这一段的拦截.因这一段大气阻力极小,导弹惯性飞行,只受到地球的引力,所以这一段轨道为比较标准的椭圆轨道,以一般洲际弹道导弹远地点1 000 km为例来计算弹道导弹的飞行参数[2]万有引力常量
G=6.67×10-11N·m2/kg2
地球质量
M=6.0×1024kg
地球半径
R=6 400 km
设A地坐标(3 200,5 542.56) km,B地坐标
(-3 200,5 542.56) km,当导弹飞行到坐标(x,y)位置时,根据万有引力和牛顿第二定律有[3]
得到
其中
1.2 用Excel建立数据模型[4]
取时间间隔Δt,足够小,那么在Δt时间内的导弹的运动看成是匀变速运动,得到
1.3 建立公式形成数据
单元格A1~H1,依次命名如图3所示.

图3 单元格A1~H1依次命名
单元格A2~H2,初始化
在单元格A3~H3依次输入公式如下:
单元格A:“=A2+F2*H2+0.5*D2*H2^2”即
单元格B:“=B2+G2*H2+0.5*E2*H2^2”即
单元格C:“=(A2^2+B2^2)^0.5”即
单元格D:“=-400 200 000 000 000*A3/C3^3”
即
GM=4.002×1014
单元格E:“=-400 200 000 000 000*B3/C3^3”
即
GM=4.002×1014
单元格F:“=F2+D2*H2”即
单元格G:“=G2+E2*H2”即
单元格H:“=H2”即保持Δt
选择单元格A~H,拖动右下十字光标,智能复制公式,形成数据列,根据需要决定数据的多少,选中A和B列,插入图表即得弹道轨道图(图4),图中正圆为地球.
可以看到导弹轨道是以地心为一个焦点的椭圆轨道,轨道没有闭合可以多拉几个数据让其闭合,借助计算机利用Excel建立的数据模型来画出导弹的运动轨道[4].
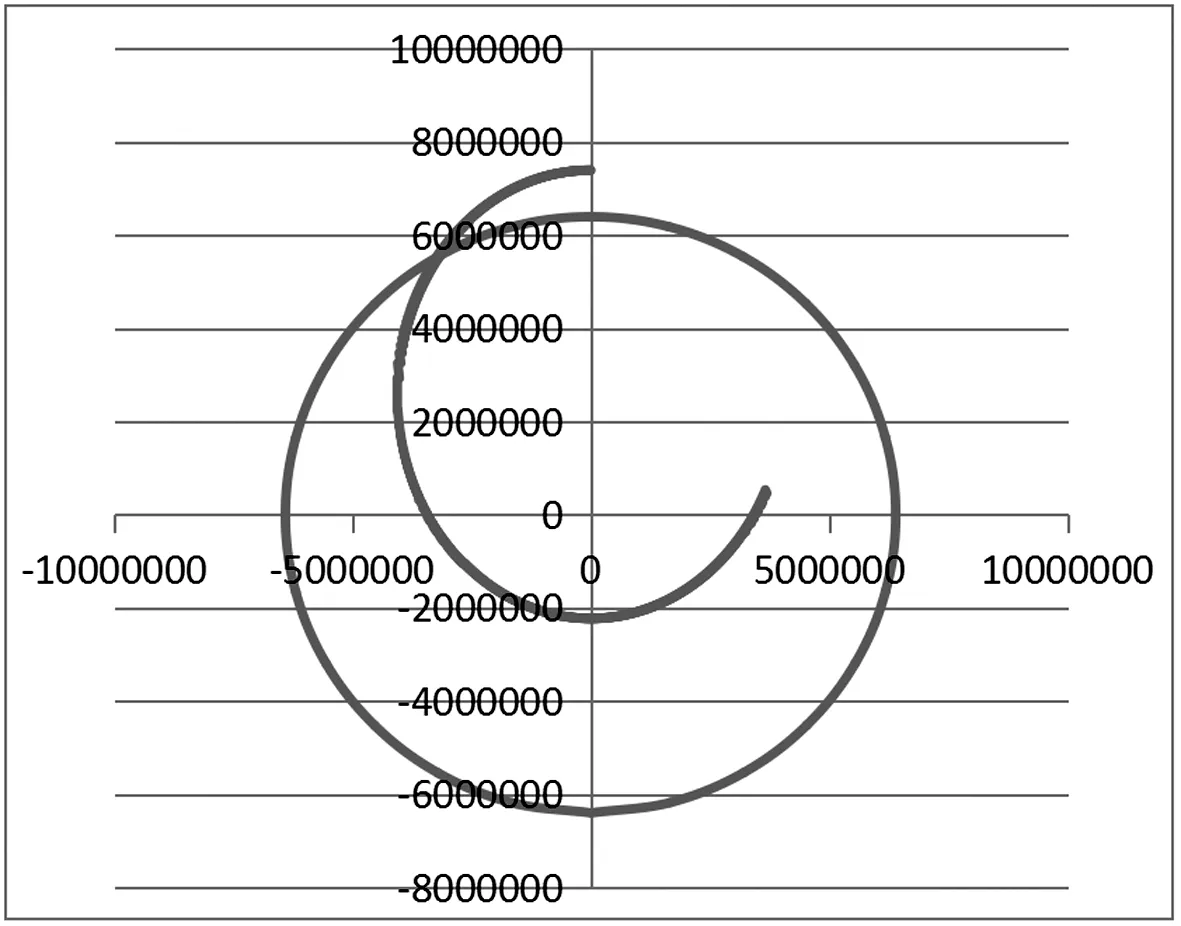
图4 得到的弹道轨图
按理论分析,如果远地点确定,远地点的速度确定,那么椭圆轨道是确定的,所以取远地点7 400 km,打到B(-3 200,5 542.56) km,经多次尝试在远地点速度vx=-4.996 km/s.导弹即能打到B点时,由Excel计算数据得到到B点时速度参数为vBx=-3 546.75 m/s,vBy=-5 412 m/s,如图5所示,根据对称性可知,此导弹在A位置的发射参数vAx=-3 546.75 m/s,vAy=5 412 m/s.

图5 由Excel计算数据
现在把初始状态设成为xA=3 200 km,yA=
5 542.56 Km,vAx=-3 546.75 m/s,vAy=5 412 m/s,得到有A地发射的导弹轨道,如图6所示(圆形为地球),能精确命中B地xB=-3 200 km,yB=5 542.56 km

图6 由A点发射的导弹轨道
Excel的优势是既有数据运算,又可以描绘轨迹,而且不需要高深的弹道理论和编程知识,中学知识完全能应用自如.
2 反导拦截弹的轨道计算
反导系统有雷达采集到弹道导弹的有效弹道参数,找准时机发射拦截弹,把导弹拦截于再入大气层之前,最好的拦截点为即将入大气层的附近段,设拦截弹由于火箭动力,保持6 km/s速度不变,有卫星制导始终正对目标导弹方向,如图2建立坐标;
由题意可知,拦截弹起始坐标在B(-3 200,
5 542.56) km.
在t时刻拦截弹坐标(x1,y1),导弹的坐标(x2,y2),则
拦截弹的方向角
经过很小的时间间隔Δt,拦截弹的坐标变为(x1+v1Δtcosθ,y1+v1Δtsinθ)
导弹坐标变为(x2(n+1),y2(n+1)),见弹道导弹数据.
打开原Excel数据,留一空行(一定要留出,否则与导弹数据发生关联)
A列输入:“x1+v1Δtcosθ”;
B列输入:“y1+v1Δtsinθ”;
C列输入:
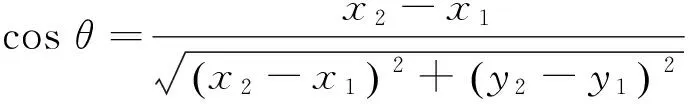
D列输入:

Δt取0.3,接近时可以取得更小点,以便更精确.选A和B列数据插入图表得到拦截弹轨迹如图8所示(Δt取得越小轨道越精确).
2016-10-12)
