迭代学习控制的参考信号初始修正方法
2017-09-11严求真孙明轩蔡建平
严求真 孙明轩 蔡建平
迭代学习控制的参考信号初始修正方法
严求真1孙明轩2蔡建平3
针对一类非参数不确定系统,提出状态受限迭代学习控制的参考信号初始修正方法,以解决任意初态下的状态受限轨迹跟踪问题.通过构造修正参考信号,利用一种新型的障碍Lyapunov函数设计迭代学习控制系统,采用鲁棒方法与学习方法相结合的策略处理非参数不确定性,经过足够多次迭代后,可实现系统状态在整个作业区间上对修正参考信号的零误差跟踪,以及在预设作业区间上对参考信号的零误差跟踪.同时,将滤波误差约束于预设的界内,并由此实现对系统状态在各次迭代运行过程中的约束.仿真结果表明了本文所提控制方法的有效性.
迭代学习控制,初值问题,非参数不确定性,障碍Lyapunov函数
在工业实际中,存在着大量在有限区间上重复运行的系统或设备,例如机械臂、磁盘驱动器和逆变电路等.问世于上世纪80年代的迭代学习控制技术,适合为这类重复作业对象设计轨迹跟踪控制器.采用迭代学习控制技术设计控制系统时,不需对受控对象的模型精确已知,其策略是利用跟踪误差不断修正控制输入,经过有限次迭代,使得系统状态或系统输出以预设精度跟踪期望轨迹[1].通过三十余年的发展,学习控制的理论逐渐丰富与完善,并应用于诸多工业控制场合[2−6].
基于Lyapunov方法设计学习控制系统是当前迭代学习控制领域的热点之一[2−3].采用学习方法,可以对控制系统中的各类参数不确定性进行估计.文献[7]利用微分学习方法处理常参数不确定性,文献[3]在构造Lyapunov泛函的基础上,设计差分学习律估计时变未知参数.文献[8]采用由微分与差分相混合的学习方式估计未知常参数.非线性参数不确定性[9]与参数随迭代次数变化[10]问题也在人们的考虑之列.到目前为止,研究非参数不确定系统学习控制方法的文献数量还较少.文献[11]采用鲁棒方法处理非参数不确定性,即利用界函数设计反馈项对其予以补偿.文献[12−14]采用鲁棒方法与学习方法相结合的策略处理非参数不确定性.此外,也可采用傅立叶级数等逼近工具处理非参数不确定性[15].
常规迭代学习控制算法常假设迭代误差的初值为零,这样,经过足够多次迭代后,可以实现整个作业区间上的零误差轨迹跟踪.但在现实中,受复位条件所限,上述假设很难满足.为拓宽迭代学习控制技术在实际中的应用范围,有必要研究可在任意初始误差情形下实施的学习控制算法.在利用Lyapunov方法为连续系统设计控制器时,常见的初值问题解决方案有时变边界层、误差跟踪和初始修正等.文献[16]给出基于时变边界层的模糊学习控制方法,闭环系统的滤波误差可在足够多次迭代后,收敛至与迭代初值相关的时变死区.文献[17]研究非线性系统的误差跟踪学习方法,并将其与参考信号初始修正方法进行对比.早在上世纪90年代,人们在设计压缩映射学习控制系统时,就采用初始修正方法解决学习控制的初值问题[18].近年来,初始修正方法重新受到人们的关注[17,19].文献[20]考虑MIMO参数不确定系统的参考信号初始修正问题.文献[21−22]针对具有任意初始误差的非参数不确定系统,给出的自适应学习控制算法适用于固定初始误差情形.
最近,构造障碍Lyapunov函数设计状态/输出受限学习控制系统,引起了人们的关注.采用这种方法设计控制器,可以对迭代学习过程中的状态/输出进行约束,从而增强系统的鲁棒性.文献[23−24]分别考虑输出受限情形和状态受限情形下的重复学习控制算法.文献[25]给出一种形式简单的二次分式型障碍Lyapunov函数构造方案,在迭代学习过程中实现对系统状态的整体约束.文献[26]研究迭代误差初值任意情形下的状态受限误差跟踪学习控制方案,同时解决初值问题和状态约束问题.文献[27]利用时变神经网络估计不确定性,结合时变边界层方法设计状态受限学习控制系统.
本文研究非参数不确定学习控制系统的初值问题及状态受限问题,在利用参考信号初始修正方法解决初值问题的同时,采用障碍Lyapunov函数设计学习控制系统,对各次迭代学习过程中的系统状态予以约束.为了提高利用障碍Lyapunov函数设计学习控制器时的便捷性,本文构造了一种新型的障碍Lyapunov函数,改进了已有的同类设计方案.经过足够多次迭代后,藉由系统状态对修正参考信号在整个作业区间的完全跟踪,获得系统状态对参考信号在预设部分作业区间上的完全跟踪.在各次迭代过程中,闭环系统中的滤波误差被约束于预设的界内,由此实现对系统状态在各次迭代运行过程中的约束.文中算法采用鲁棒学习控制方法处理非参数不确定性,并根据学习方法估计鲁棒项的增益系数,克服了以往同类算法中在某些场合应用时,可能出现的增益过大之不足.
1 问题的提出
考虑在有限时间[0,T]上迭代运行的非参数不确定系统:
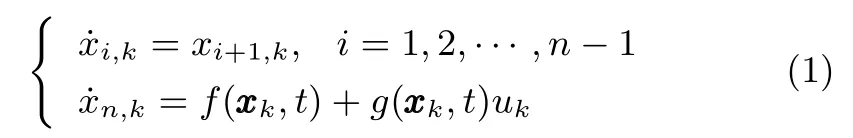

不失一般性[23],系统(1)中的不确定性满足下述假设:假设 1.对于 ∀ ξ1∈ Rn,∀ ξ2∈ Rn,函数 f(·,·) 和 g(·,·)分别满足
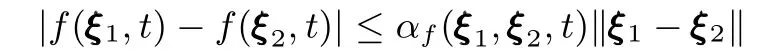
与
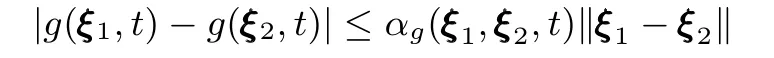
其中,αf(·,·,·) 和 αg(·,·,·) 为非负连续函数.
本文的控制目标是设计uk,实现对在 [tδ,T]上的完全跟踪(0<tδ<T).为了实现该任务,下文构造修正参考信号.,为一常数,但具体大小不需已知.
2 修正参考信号的构造
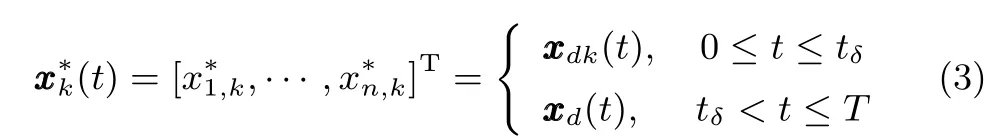


此处,

本文中,xn+1,k(t)表示˙xn,k(t),xn+1,k(0)=˙xn,k(0).上文所构造的修正参考信号,在t=tδ处的导数是连续的.可以看出,上文给出的构造方法比较简便,易于实施.
3 控制器的设计
在t∈[0,T]上,定义

选择合适的正实数 ci(i=1,2,···,n−1),使得多项式Δ(λ)= λn−1+cn−1λn−2+···+c2λ +c1为 Hurwitz 多项式,且使的范数.为叙述方便,分别记为.在不引起混淆时,为叙述简便,文中将函数的时间变量t略去.
由式(7)可得
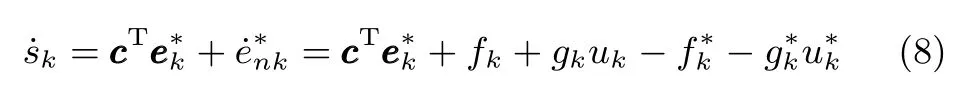
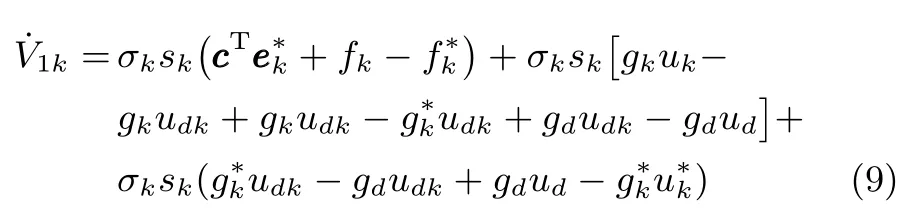


对上式两边同取范数,根据Bellman-Gronwall引理,
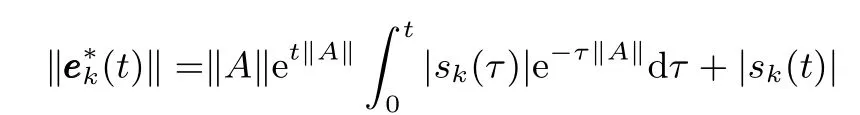
根据积分中值定理,存在一未知常数ωk1(t)∈[0,1],满足

于是由上述两式可得

利用积分中值定理,由上式可以推出,存在ωk2(t)∈[0,1],满足
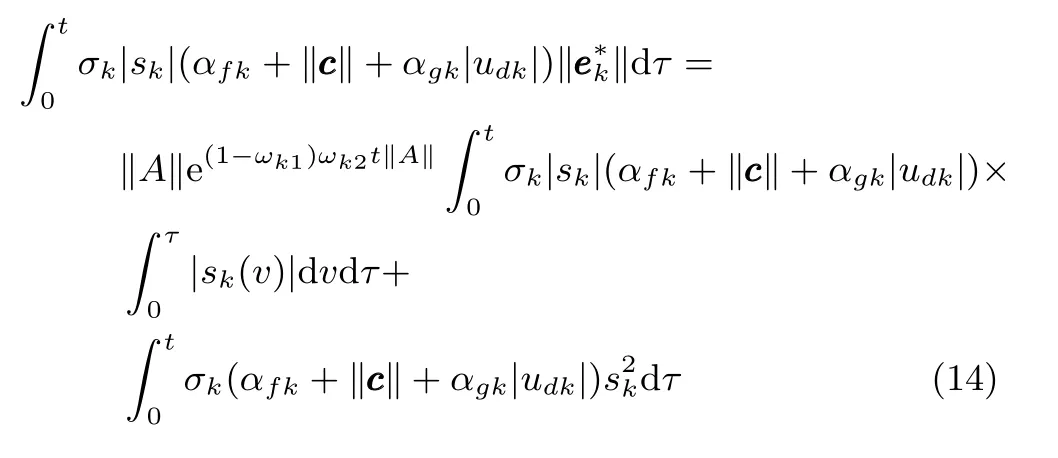
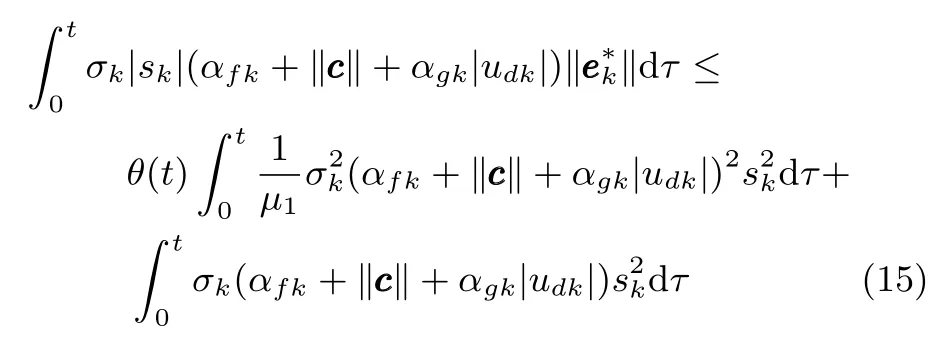
式中,θ(t)=µ1t‖A‖e¯ωt‖A‖,µ1>0为设计参数.将式(15)的结果应用于式(11),
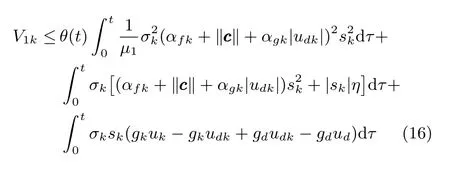
由此,设计控制器
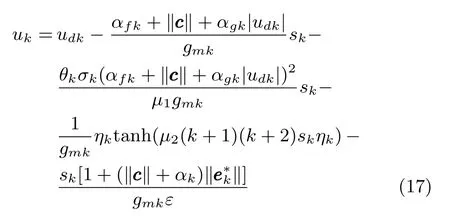
及相应的学习律

此处,ηk为η的估计值,θk为θ的估计值,µ2>0为设计参数,γ1> 0,γ2> 0,γ3> 0,ε≫ 0.本文中,sat(·)的定义为:对于∈R,为对应的限幅.学习律(18)~(20)均采用完全限幅学习方法估计被学习量.

根据sk与之间的不等式关系[21−22,26]
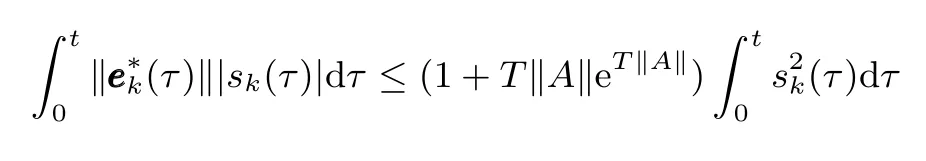
控制器(17)也可改为

在T‖A‖的取值较大场合,(1+T‖A‖eT‖A‖)是个很大的数.本文设计控制系统时,没有采用上述控制器设计方案,而是利用学习方法估计θ,有利于减小设计中的保守性.
注 1.迄今,人们已经构造了多种障碍Lyapunov函数[23−26],例如等,利用这些障碍Lyapunov函数设计控制器,都可以有效地对系统状态或输出进行相应的约束.本文构造了一种新型的障碍Lyapunov函数,其具有的一个特点是.本文根据该障碍Lyapunov函数设计控制器时,利用了这一特点,具体而言:在由式(14)推出式(15)的过程中,利用了.
1.2方法两组患者均在全麻状态下实施手术,需注意让患者在手术前6~8h严禁进食进水,以免术中因麻药反应产生呕吐,呕吐物堵塞气管造成危险。对照组实施开放型手术,即将脑颅打开将瘤体清除。观察组采用显微手术方式治疗,具体操作如下。
4 收敛性分析
根据上文给出的控制设计,闭环系统具有的性质可总结为定理1.

并确保在各次迭代运行过程中,|sk|<bs成立.
证明.1)变量有界性及系统状态的受限性
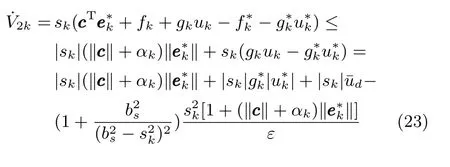
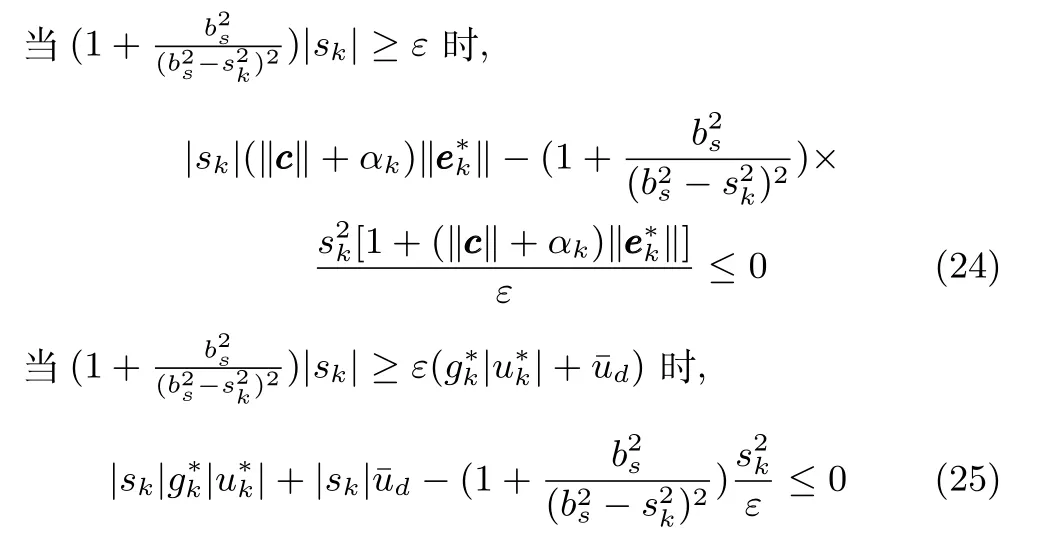
记h=|sk|,注意到:1)在每次迭代的开始时刻,sk=0;2)函数在h∈[0,bs)区间内单调递增,且limh→bs−ν(h)=+∞.因此,当在[0,bs)内的|sk|足够大时,必有

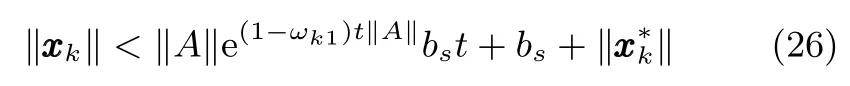
可见,系统状态在各次迭代运行过程中均受到相应的约束.
2)误差收敛性

根据式(27),当k>0时,

根据学习律(18),

类似地,根据学习律(19)及(20),分别可以推出
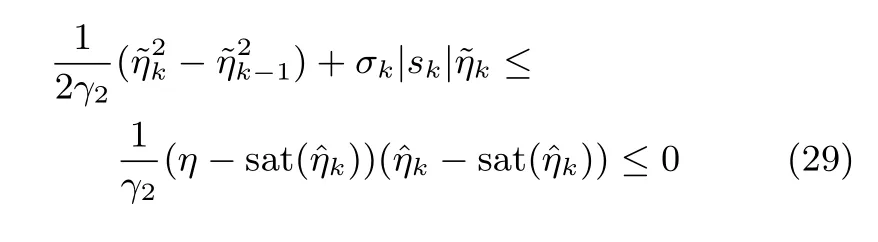
及
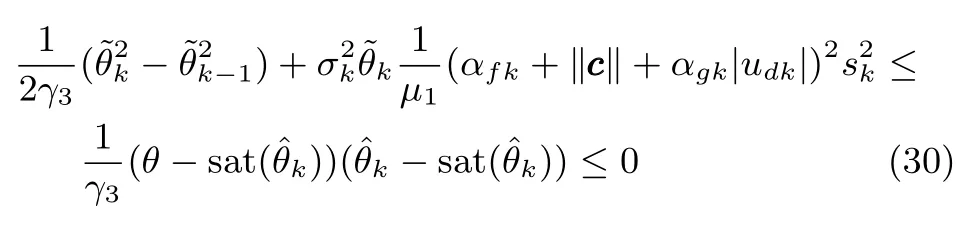
综合以上四式,有

进一步地,

5 仿真算例
考虑在[0,T]上运行的非线性系统
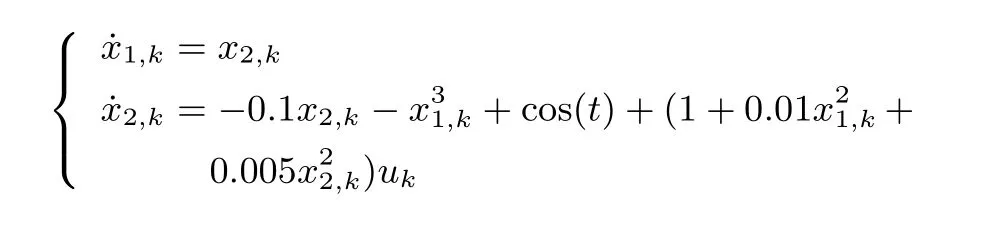


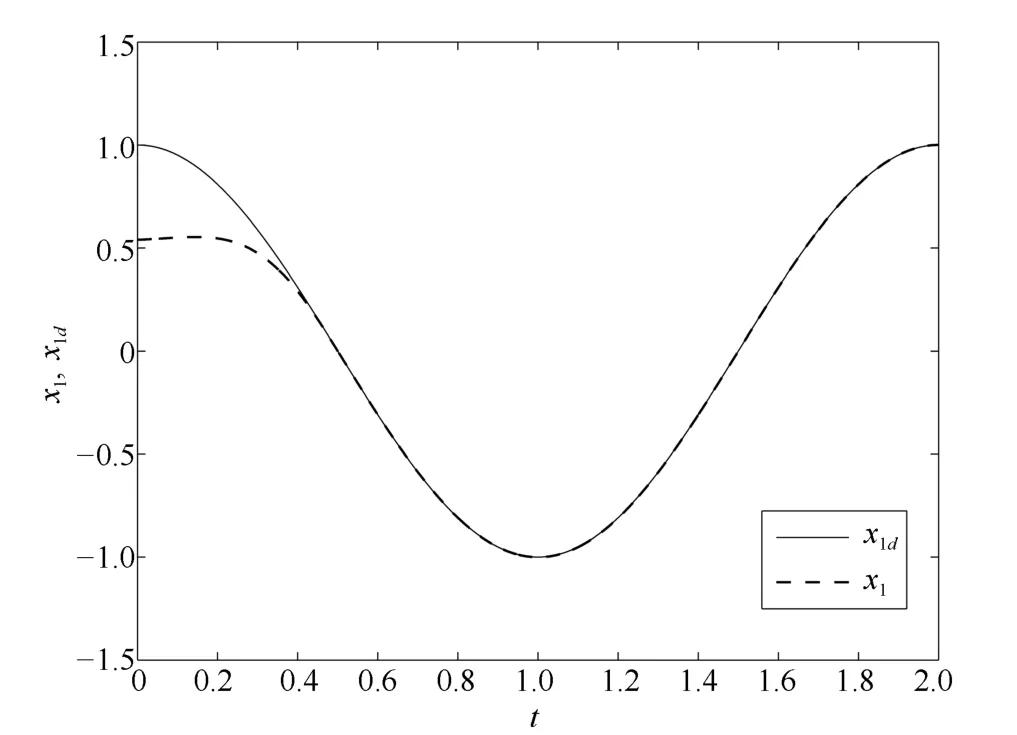
图1 x1及其期望轨迹x1dFig.1 x1and its desired trajectory x1d
为对比起见,采用无约束的初始修正学习控制律

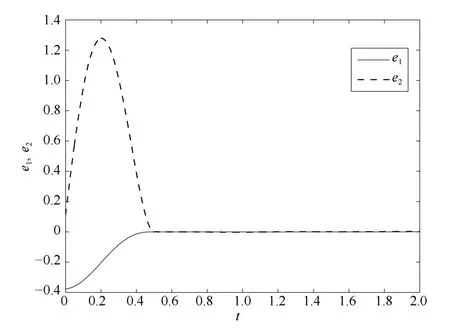
图3 误差e1和e2Fig.3 The errors e1and e2
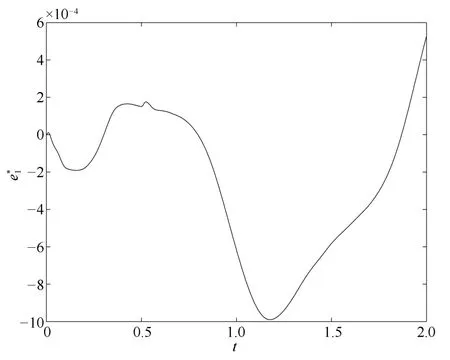
图4 修正误差Fig.4 The recti fi ed error

图5 修正误差Fig.5 The recti fi ed error
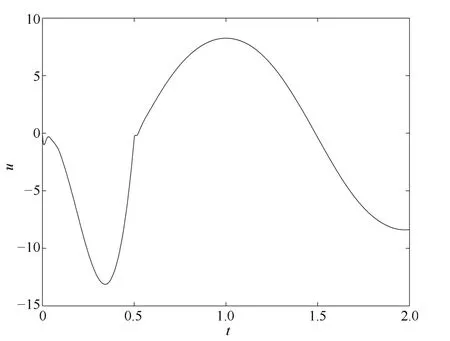
图6 控制输入Fig.6 Control input
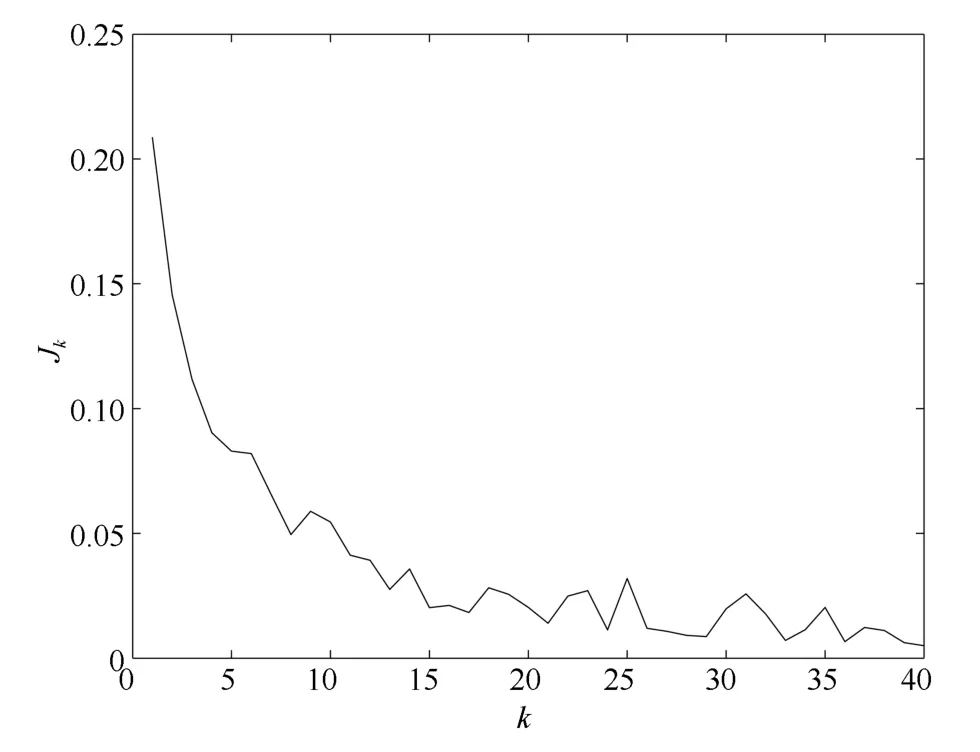
图7 状态受限情形下Jk的收敛过程Fig.7 The history of Jkin the case of constraint
进行仿真,式中,
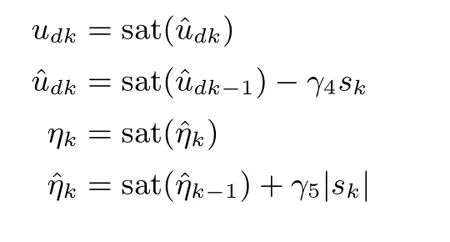
仿真结果表明,利用本文给出的状态受限参考信号初始修正方法设计学习控制器,可以解决非参数不确定学习控制系统的初值问题,实现系统状态对修正参考信号在整个作业区间上的完全跟踪,并确保将各次迭代过程中的滤波误差约束于预设的界内,对系统状态予以约束.上述结果说明了本文所提控制方法的有效性.
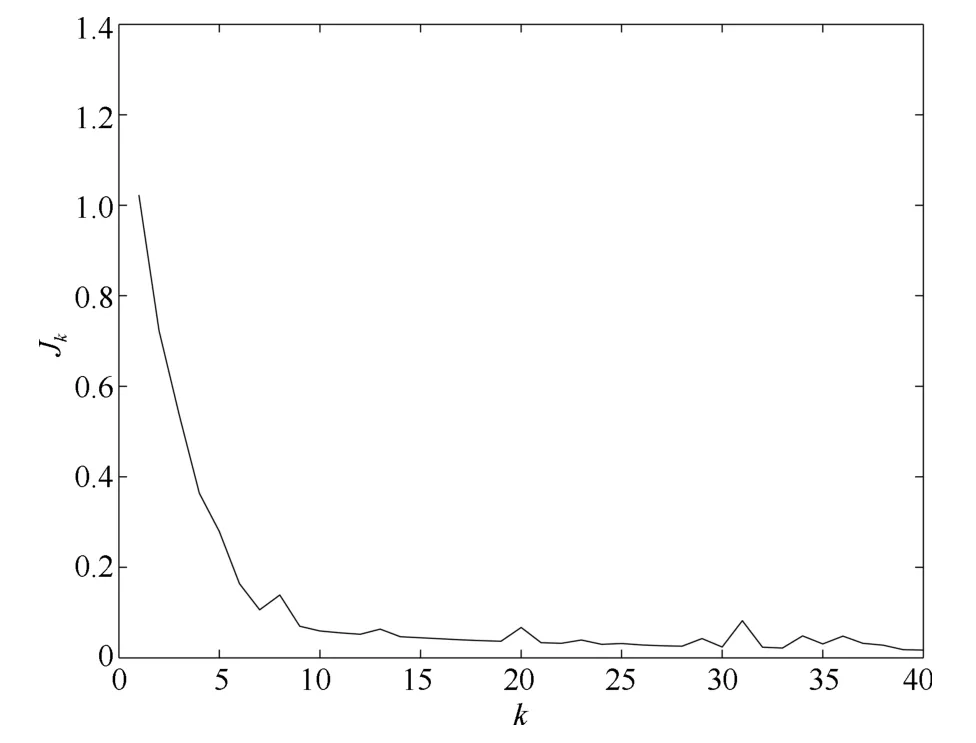
图8 Jk收敛过程Fig.8 The history of Jk
6 结论
本文提出状态受限迭代学习控制的参考信号初始修正方法,解决非参数不确定系统在任意初态情形下的状态受限轨迹跟踪问题.文中给出了修正参考信号构造方案,并利用一种新型的障碍Lyapunov函数设计迭代学习控制器,采用鲁棒学习控制方法处理非参数不确定性.经过足够多次迭代后,藉由系统状态对修正参考信号在整个作业区间的完全跟踪,获得系统状态对参考信号在预设部分作业区间上的完全跟踪.在各次迭代过程中,闭环系统中的滤波误差被约束于预设的界内,由此实现对系统状态在各次迭代运行过程中的约束.本文采用学习方法估计鲁棒项的增益系数,克服了以往同类算法在某些场合应用时可能出现的增益过大现象.
1 Arimoto S,Kawamura S,Miyazaki F.Bettering operation of robots by learning.Journal of Field Robotics,1984,1(2):123−140
2 Dixon W E,Zergeroglu E,Dawson D M,Costic B T.Repetitive learning control:a Lyapunov-based approach.IEEE Transactions on Systems,Man,and Cybernetics,Part B(Cybernetics),2002,32(4):538−545
3 Xu J X,Tan Y.A composite energy function-based learning control approach for nonlinear systems with time-varying parametric uncertainties.IEEE Transactions on Automatic Control,2002,47(11):1940−1945
4 Zhang Yu-Dong,Fang Yong-Chun.Learning control for systems with saturated output.Acta Automatica Sinica,2011,37(1):92−98(张玉东,方勇纯.一类输出饱和系统的学习控制算法研究.自动化学报,2011,37(1):92−98)
5 Zhang Li,Liu Shan.Basis function based adaptive iterative learning control for non-minimum phase systems.Acta Automatica Sinica,2014,40(12):2716−2725
(张黎,刘山.非最小相位系统的基函数型自适应迭代学习控制.自动化学报,2014,40(12):2716−2725)
6 Bu Xu-Hui,Hou Zhong-Sheng,Yu Fa-Shan,Fu Zi-Yi.Iterative learning control for trajectory tracking of farm vehicles.Acta Automatica Sinica,2014,40(2):368−372
(卜旭辉,侯忠生,余发山,付子义.基于迭代学习的农业车辆路径跟踪控制.自动化学报,2014,40(2):368−372)
7 French M,Rogers E.Non-linear iterative learning by an adaptive Lyapunov technique.International Journal of Control,2000,73(10):840−850
8 Tayebi A,Chien C J.A uni fi ed adaptive iterative learning control framework for uncertain nonlinear systems.IEEE Transactions on Automatic Control,2007,52(10):1907−1913
9 Chen Wei-Sheng,Wang Yuan-Liang,Li Jun-Min.Adaptive learning control for nonlinearly parameterized systems with periodically time-varying delays.Acta Automatica Sinica,2008,34(12):1556−1560
(陈为胜,王元亮,李俊民.周期时变时滞非线性参数化系统的自适应学习控制.自动化学报,2008,34(12):1556−1560)
10 Yin C K,Xu J X,Hou Z S.A high-order internal model based iterative learning control scheme for nonlinear systems with time-iteration-varying parameters.IEEE Transactions on Automatic Control,2010,55(11):2665−2670
11 Ham C,Qu Z.A new learning control based on the Lyapunov direct method.In:Proceedings of Southcon/94 Conference Record.Orlando,USA:IEEE,1994.121−125
12 Xu J X,Yan R.On repetitive learning control for periodic tracking tasks.IEEE Transactions on Automatic Control,2006,51(11):1842−1848
13 Marino R,Tomei P,Verrelli C M.Robust adaptive learning control for nonlinear systems with extended matching unstructured uncertainties.International Journal of Robust and Nonlinear Control,2012,22(6):645−675
14 Chen Peng-Nian,Qin Hua-Shu,Fang Xue-Yi.Iterative learning control for uncertain nonlinear systems with time-varying control gain.Journal of Systems Science and Mathematical Sciences,2012,32(6):693−704
(陈彭年,秦化淑,方学毅.控制增益时变的非线性系统的迭代学习控制.系统科学与数学,2012,32(6):693−704)
15 Liuzzo S,Marino R,Tomei P.Adaptive learning control of nonlinear systems by output error feedback.IEEE Transactions on Automatic Control,2007,52(7):1232−1248
16 Chien C J,Hsu C T,Yao C Y.Fuzzy system-based adaptive iterative learning control for nonlinear plants with initial state errors.IEEE Transactions on Fuzzy Systems,2004,12(5):724−732
17 Sun M X,Yan Q Z.Error tracking of iterative learning control systems.Acta Automatica Sinica,2013,39(3):251−262
18 Sun Ming-Xuan,Huang Bao-Jian.Iterative Learning Control.Beijing: NationalDefenceIndustry Press,1999.182−184
(孙明轩,黄宝健.迭代学习控制.北京:国防工业出版社,1999.182−184)
19 Yan Qiu-Zhen,Sun Ming-Xuan,Li He.Iterative learning control for nonlinear uncertain systems with arbitrary initial state.Acta Automatica Sinica,2016,42(4):545−555
(严求真,孙明轩,李鹤.任意初值非线性不确定系统的迭代学习控制.自动化学报,2016,42(4):545−555)
20 Li X D,Chow T W S,Cheng L L.Adaptive iterative learning control of non-linear MIMO continuous systems with iteration-varying initial error and reference trajectory.International Journal of Systems Science,2013,44(4):786−794
21 Li Xiang-Yang.Iterative learning control for a class of nonlinear time-varying system.Control Theory&Applications,2014,31(8):1087−1093
(李向阳.一类非线性时变系统的迭代学习控制.控制理论与应用,2014,31(8):1087−1093)
22 Li Xiang-Yang.Iterative learning control based on fi nite time tracking di ff erentiator.Acta Automatica Sinica,2014,40(7):1366−1375
(李向阳.基于有限时间跟踪微分器的迭代学习控制.自动化学报,2014,40(7):1366−1375)
23 Jin X,Xu J X.Iterative learning control for outputconstrained systems with both parametric and nonparametric uncertainties.Automatica,2013,49(8):2508−2516
24 Xu J X,Jin X.State-constrained iterative learning control for a class of MIMO systems.IEEE Transactions on Automatic Control,2013,58(5):1322−1327
25 Sun Ming-Xuan,Zhang Wei-Bo,Yan Qiu-Zhen.Constrained iterative learning control of a class of non-parametric uncertain systems.Control Theory&Applications,2014,31(4):479−484
(孙明轩,张伟博,严求真.非参数不确定系统约束迭代学习控制.控制理论与应用,2014,31(4):479−484)
26 Yan Qiu-Zhen,Sun Ming-Xuan.Error-tracking iterative learning control with state constrained for nonparametric uncertain systems.Control Theory&Applications,2015,32(7):895−901
(严求真,孙明轩.非参数不确定系统状态受限误差跟踪学习控制方法.控制理论与应用,2015,32(7):895−901)
27 Yu Qiong-Xia,Hou Zhong-Sheng.Adaptive iterative learning control for a class of non-parametric uncertain systems.Journal of Systems Science and Mathematical Sciences,2016,36(1):1−13(余琼霞,侯忠生.非参数不确定系统的自适应迭代学习控制.系统科学与数学,2016,36(1):1−13)
28 Zhuang Kai-Yu,Zhang Ke-Qin,Su Hong-Ye,Chu Jian.Terminal sliding mode control for high-order nonlinear dynamic systems.Journal of Zhejiang University(Engineering Science),2002,36(5):482−485,539
(庄开宇,张克勤,苏宏业,褚健.高阶非线性系统的Terminal滑模控制.浙江大学学报(工学版),2002,36(5):482−485,539)
29 Xie Hua-Ying,Sun Ming-Xuan,Jin Kui.Iterative learning controller designs with fi nite-time convergence performance.In:Proceedings of the 29th Chinese Control Conference.Beijing,China:TCCT,2010.5845−5850
(谢华英,孙明轩,金奎.有限时间收敛迭代学习控制器设计.见:第 29届中国控制会议论文集.北京:中国自动化学会,2010.5845−5850)
严求真 浙江水利水电学院信息工程学院讲师.主要研究方向为学习控制.E-mail:zjyqz@126.com
(YAN Qiu-Zhen Lecture at the College of Information Engineering,Zhejiang University of Water Resources and Electric Power.His main research interest is learning control.)
孙明轩 浙江工业大学信息工程学院教授.主要研究方向为学习控制.本文通信作者.E-mail:mxsun@zjut.edu.cn
(SUN Ming-Xuan Professor at the College of Information Engineering,Zhejiang University of Technology.His main research interest is learning control.Corresponding author of this paper.)
蔡建平 浙江水利水电学院应用数学研究所副教授.主要研究方向为自适应控制.E-mail:caijp@zjweu.edu.cn
(CAI Jian-Ping Associate professor at the Institute of Applied Mathematics,Zhejiang University of Water Resources and Electric Power.His main research interest is adaptive control.)
Reference-signal Rectifying Method of Iterative Learning Control
YAN Qiu-Zhen1SUN Ming-Xuan2CAI Jian-Ping3
This paper presents a reference-signal rectifying method of iterative learning control to address the trajectorytracking problem for a class of state-constrained uncertain systems,in the presence of arbitrary initial states.For design of the iterative learning control scheme,a recti fi ed reference signal is constructed and a new type of barrier Lyapunov function is used.In order to deal with the nonparametric uncertainties,a robust learning approach is applied.It is shown that the closedloop system′s state follows the recti fi ed reference signal perfectly over the entire time interval as iteration increases.In turn,the system state tracks the reference signal on the speci fi ed interval.During each iteration,the fi ltering-error is constrained in the pre-speci fi ed region,and the system state is thus constrained.Numerical results are presented to demonstrate the e ff ectiveness of the learning control scheme.
Iterative learning control,initial condition problem,nonparametric uncertainties,barrier Lyapunov function
March 26,2016;accepted September 11,2016国家自然科学基金(61374103,61573320,61573322),浙江省公益技术研究项目(2016C32093,2017C33155),浙江省教育厅科研项目(Y201635861)资助
严求真,孙明轩,蔡建平.迭代学习控制的参考信号初始修正方法.自动化学报,2017,43(8):1470−1477
Yan Qiu-Zhen,Sun Ming-Xuan,Cai Jian-Ping.Reference-signal rectifying method of iterative learning control.Acta Automatica Sinica,2017,43(8):1470−1477Hangzhou 310023 3.Institute of Applied Mathematics,Zhejiang University of Water Resources and Electric Power,Hangzhou 310018
2016-03-26 录用日期2016-09-11
Supported by National Natural Science Foundation of China(61374103,61573320,61573322),Science and Technology Project of Zhejiang Province(2016C32093,2017C33155),Scienti fi c Research Project of Education Department of Zhejiang Province(Y201635861)
本文责任编委 王聪
Recommended by Associate Editor WANG Cong
1.浙江水利水电学院信息工程学院 杭州 310018 2.浙江工业大学信息工程学院 杭州 310023 3.浙江水利水电学院应用数学研究所 杭州 310018
1. College of Information Engineering,Zhejiang University of Water Resources and Electric Power,Hangzhou 310018 2.College of Information Engineering,Zhejiang University of Technology,
DOI10.16383/j.aas.2017.c160292
