Globally Exponential Stability of Memristive Neural Networks With Time-varying Delays and Synchronous Switching
2017-09-11YinluJiangChuandongLi
Yinlu Jiang Chuandong Li
Globally Exponential Stability of Memristive Neural Networks With Time-varying Delays and Synchronous Switching
Yinlu Jiang1Chuandong Li1
In this paper,we formulate and investigate a memristive neural networks with time-varying delays and synchronous switching.Conditions are derived which ensure the existence of an equilibrium point and uniform stability for state trajectories of the memristive neural network.The analysis in the paper employs results from the theory of Lyapunov function.Moreover,the proposed stability conditions are straightforward and convenient which can re fl ect the impact of time-varying delays on the stability.The simulation results demonstrate the e ff ectiveness of the theoretical results.
Lyapunov function,memristive neural networks,synchronous switching,time-varying delays
DOI10.16383/j.aas.2017.e150066
1 Introduction
The “memristor”,an abbreviation for memory resistor,is the fourth basic circuit element along with resistors,capacitors and inductors which were studied by Chua[1]in 1971.Chua et al.[2]showed that the value of the memristor,called memristance,is the function of electric charge q given as,where ϕ represents the magnetic fl ux.On May 1,2008,the Hewlett-Packard(HP)research team proudly announced that they had built a prototype of the memristor with an official publication in Nature[3].
As we know,the memristive neural network is a prerequisite in many applications such as signal processing,pattern recognition,systems control and intelligent circuit[4]−[11].Because of the special nonlinear structure and its important applications,the theoretical analysis of memristive neural network is a very important issue for research.Memristive switching neural network is one of the study branches.Switching system is a hybrid system,which consists of several subsystems and a switching rule.Neural networks with switching behavior are called switching neural networks.Because of the special nature of memristor,there are many researchers who have been interested in investigating memristive switching neural networks[12]−[15].
It is known that time delay a ff ects the dynamic behaviors of neural networks enormously,and delay-dependent stability criteria are of little conservatism,therefore many important results have been established for time-delay system[16]−[18].According to the feature of memristor and the current characteristics,we know there exists a fi xed switching time between memristors’two states,thus,thememristor is a switching system itself.Motivated by the above discussion,the main aim in this paper was to establish a memristive neural network with time-varying delays and put some external switching signals which are synchronous with the fi xed switching time between memristors’two states.This memristive system is not only a timedelay system but also a switching system,we can call the system memristive neural networks with time-varying delays and synchronous switching.This is a new system that is never studied before,we will establish stability criteria for this system in this paper.The method of this paper can be extended to study some other memristive neural networks.
According to the feature of memristor and the current characteristics,in this paper,we apply a simple mathematical model of the memristance as follows[19]:
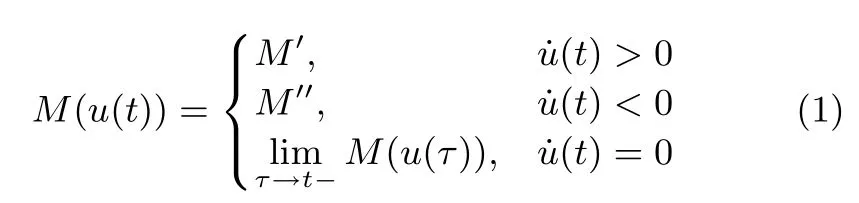
where u is the voltage applied to the memristor,˙u(t)is the derivative of u with respect to time t.M′≤ M′′,M′and M′′are the memristances when˙u(t)>0 and˙u(t)<0 respectively.When˙u(t)=0,limτ→t−M(u(τ))means that the memristance keeps the current value.
The rest of this paper is organized as follows.In Section 2,we put forward a memristive neural network with time-varying delays and synchronous switching model,then make a brief description.In Section 3,we analyze the system in brief via Lyapunov function.In Section 4,one example is given to illustrate our results.Finally,in Section 5 we give the conclusion,in Section 6 we give the acknowledgments.
2 Model Description
We consider the following memristive neural networks with time-varying delays and synchronous switching model:

where zi(t)is the state variable of the ith neuron,γ= σ(t)is the switching signal which takes value in the fi nite set Σ={1,2,...,N},diγis the ith neuron’s self-feedback connection weight at the switching signal of γ,aij(zi− zj)γand bij(zi−zj)γare,respectively,memristive connection weights and those associated with time delays at the switching signal of γ,Siγis the external constant inputs at the switching signal of γ, τij(t)is time-varying delays for the system.n denotes the number of neurons in the indicated neural networks.(·)and(·)are the ith activation functions and those associated with time delays,respectively.
System(2)can be rewritten in the following vector form
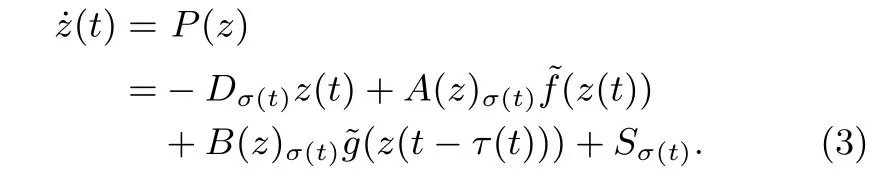
By applying the theories of set-valued maps and di ff erential inclusions,the memristive neural network(3)hasthe same solution set as the following di ff erential inclusion equation[19]−[21]:
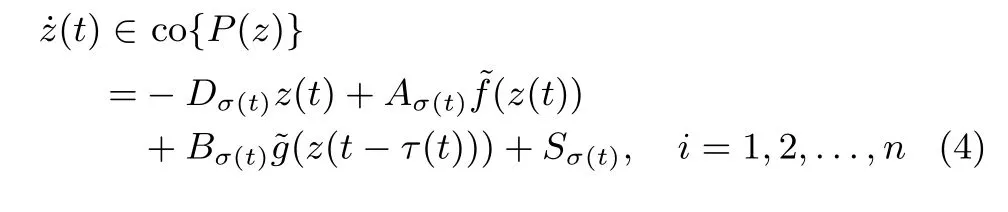
where Dγ=diag(d1γ,d2γ,...,dnγ),γ ∈ {1,2,...,N}.For some time t,σ(t)= γ,we say that ith neural network(Di,Ai,Bi)is activated at time t.Assume that the function σ(t)is right-continuous,that is,σ(t)= σ(t+).The time t is called the switching time if σ(t)/= σ(t−).And

Moreover,we assume that the initial conditions of the system(4)are of the form

where φi(·)denote real-valued continuous functions de fi ned on[−τ,0].
Suppose thatis an equilibrium point of system(2).Let x(t)=z(t)− z∗,then system(4)can be rewritten as follows

Transform(6)into the following form


The initial conditions of system(4)will be transformed into the following form

The following assumptions and de fi nition are made on system(2)throughout this paper.
Assumption 1:There exist positive constants Fi,Gi,i=1,2,...,n,and fi(0)=0,gi(0)=0 such that,for all arguments

Assumption 2:τij:[0,+∞)→ [0,+∞)is continuously di ff erentiable,and 0≤τij≤¯τ,≤R<1.
Assumption 2 ensures that t−τijhas di ff erential inverse function denoted by ϕij(t)and.
De fi nition 1[22]:Let us consider the set-valued map φ(x)de fi ned as:

where K[U]represents the closure of convex hull of set U,i.e.,.µ[U]denotes the Lebesgue measure of set U,N is an arbitrary set with measure zero.When y(t,x)is locally bounded,there exists a setandµ()=0,such that φ(x)=co{ν :there exists a set{xi}that satis fi es xiand ν=limy(t,xi)}for any t≥0,N ⊂Rnandµ(N)=0.
3 AnalysisofMemristiveSynchronous Switching Neural Networks
Theorem 1:Assume that there exist positive constants λi(i=1,2,...,n),µ,ν ∈ [0,1],and positive constants ε such that the following condition holds:

then the trivial solution of(7)is exponentially stable,and we say the system(2)is globally exponentially stable.
Proof:We can choose the following nonnegative Lya-punov function candidate for system(7)

where t>0,and then compute the upper and right Dini derivative along the trajectories of system(7)

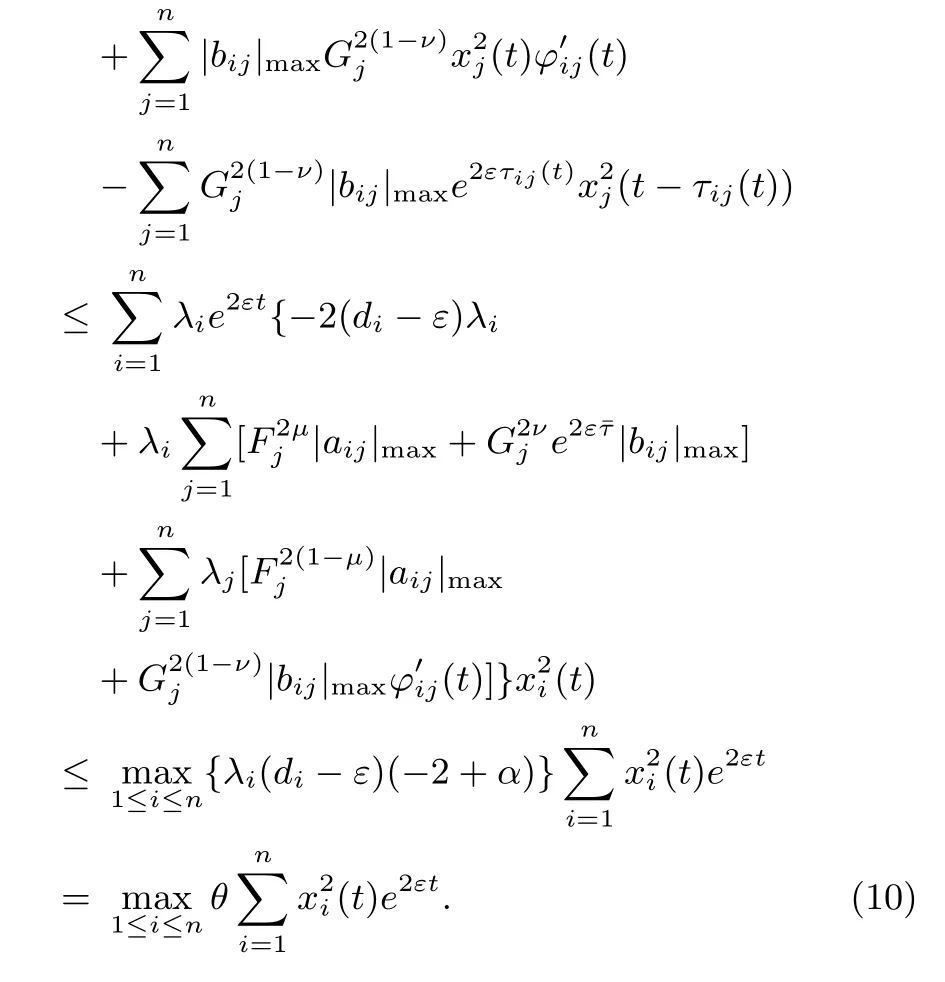
Therefore,when θ< 0

After a series of calculations according to(9),we can obtain
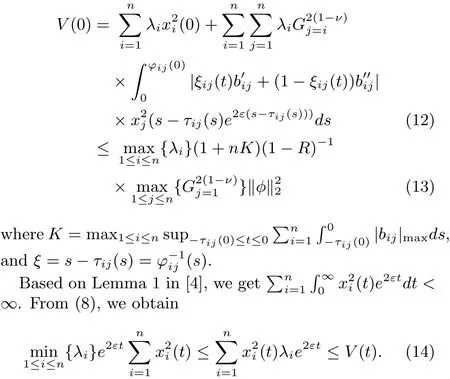
Combining(10),(11)and(13),we can get

where
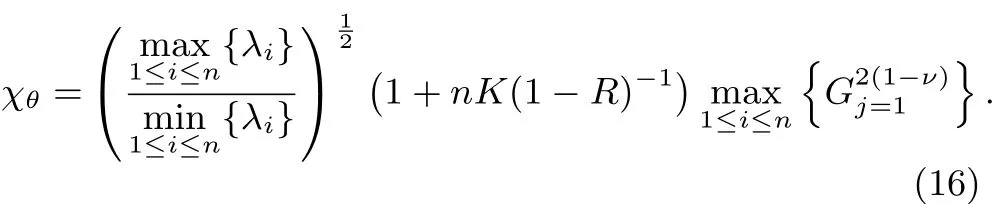
Therefore,the equilibrium point z∗of the memristive neural networks system is globally exponentially stable.Thus,the proof of Theorem 1 is completed.
The proposed criteria satisfy not only the case of binaryvalue memristor connection weight like previous results but also the case of the memristor connection weight changing continuously with the time.Moreover,we can say that the criteria of the system called memristive neural networks with time-varying delays and synchronous switching are fi rstly established.
Remark 1:In many other papers,the authors only considered the case of binary-value memristor connection weight.In the present paper,we relax this limitation and assume the memristor connection weight is changing continuously with the time,and the polarity of the voltage is also applied to the memristor.
4 An Illustrative Example
Example 1:The vector form of the memristive system(2)is as follows

Consider the switching system with Σ∈{1,2},D1=diag(1,1),D2=diag(5,5),external input S1=S2=(0,0)T,time delay τ=0.2− 0.05sin2(t).

Choose λ1= λ2=1,ε=1,it is easy to verify that those conditions satis fi ed Theorem 1,and system(2)is globally exponentially stable with convergence rate ε based on Theorem 1.Time response curves for memristive neural network with time-varying delays and synchronous switching are as shown in Fig.1.
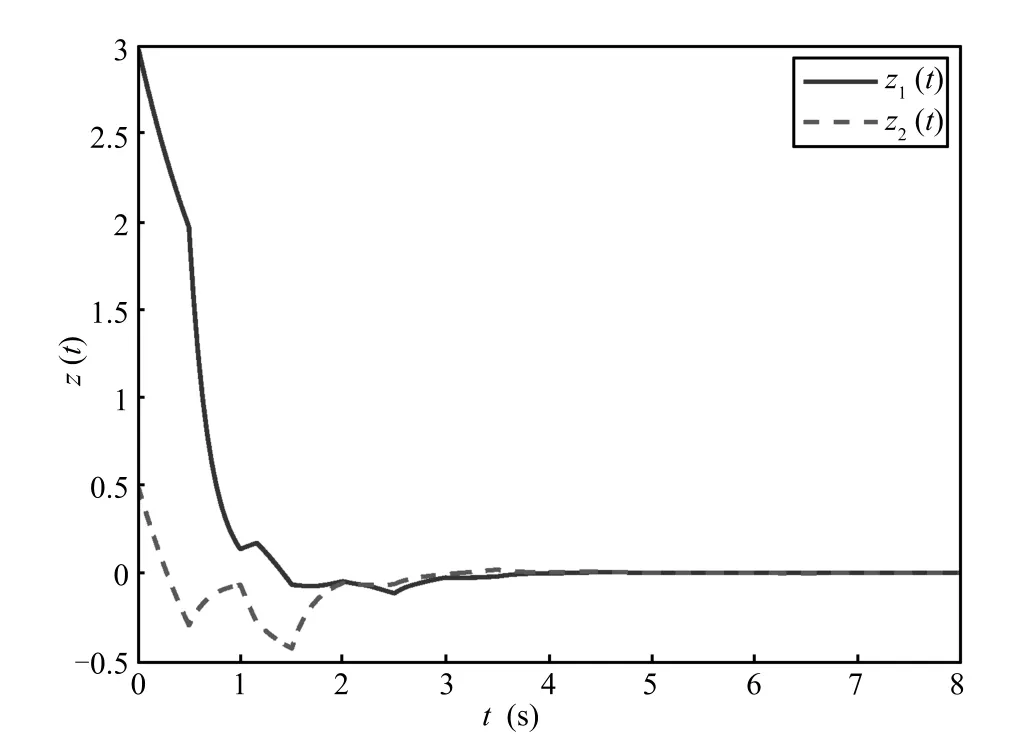
Fig.1 Time response curves for memristive neural network with time-varying delays and synchronous switching.
5 Conclusions
In this paper,we have studied the global exponential stability of memristive neural networks with time-varying delays and synchronous switching.Simple and easy criteria for exponential stability are obtained.As a result,one numerical example has been presented to illustrate e ff ectiveness of the proposed theory.The method of this paper may be extended to study some other memristive neural networks.
1 L.O.Chua,“Memristor-the missing circuit element,” IEEE Trans.Circ.Theory,vol.18,no.5,pp.507−519,Sep.1971.
2 L.O.Chua and S.M.Kang,“Memristive devices and systems,” Proc.IEEE,vol.64,no.2,pp.209−223,Feb.1976.
3 D.B.Strukov,G.S.Snider,D.R.Stewart,and R.S.Williams,“The missing memristor found,” Nature,vol.453,no.7191,pp.80−83,May2008.
4 X.F.Liao and K.W.Wong,“Global exponential stability for a class of retarded functional di ff erential equations with applications in neural networks,”J.Math.Anal.Appl.,vol.293,no.1,pp.125−148,May2004.
5 C.J.Li,C.D.Li and T.W.Huang,“Exponential stability of impulsive high-order Hop fi eld-type neural networks with delays and reaction-di ff usion,”Int.J.Computer Math.,vol.88,no.15,pp.3150−3162,May2011.
6 C.D.Li,C.J.Li and C.Liu,“Destabilizing e ff ects of impulse in delayed BAM neural networks,”Mod.Phys.Lett.B,vol.23,no.29,pp.3503−3513,Nov.2009.
7 X.F.Liao and J.B.Yu,“Robust stability for interval Hopfi eld neural networks with time delay,”IEEE Trans.Neural Netw.,vol.9,no.5,pp.1042−1045,Sep.1998.
8 C.D.Li,X.F.Liao,and K.W.Wong,“Delay-dependent and delay-independent stability criteria for cellular neural networks with delays,”Int.J.Bifurcation Chaos,vol.16,no.11,pp.3323−3340,Nov.2006.
9 X.He,C.D.Li,and Y.L.Shu,“Bogdanov-takens bifurcation in a single inertial neuron model with delay,”Neurocomputing,vol.89,pp.193−201,Jul.2012.
10 S.K.Duan,X.F.Hu,L.D.Wang,and C.D.Li,“Analog memristive memory with applications in audio signal processing,” Sci.China Inf.Sci.,vol.57,no.4,pp.1−15,Apr.2014.
11 X.Wang,C.D.Li,T.W.Huang,and S.K.Duan,“Global exponential stability of a class of memristive neural networks with time-varying delays,”Neural Comput.Appl.,vol.24,no.7−8,pp.1707−1715,Jun.2014.
12 A.V.Avizienis,H.O.Sillin,C.Martin-Olmos,H.H.Shieh,M.Aono,A.Z.Stieg,and J.K.Gimzewski,“Neuromorphic atomic switch networks,”PLoS One,vol.7,no.8,Article ID e42772,Aug.2012.
13 A.L.Wu,Y.Shen,Z.G.Zeng,and J.Zhang,“Analysis of a memristor-based switching network,”in Proc.2011 Int.Conf.Information Science and Technology(ICIST),Nanjing,China,2011,pp.1043−1046.
14 F.Z.Wang,N.Helian,S.Wu,X.Yang,Y.K.Guo,G.Lim,and M.M.Rashid,“Delayed switching applied to memristor neural networks,”J.Appl.Phys.,vol.111,no.7,Article ID 07E317,Feb.2012.
15 L.Chua, “Resistance switching memories are memristors,”Appl.Phys.A,vol.102,no.4,pp.765−783,Mar.2011.
16 Q.Han,C.D.Li,and J.J.Huang,“Estimation on error bound of lag synchronization of chaotic systems with time delay and parameter mismatch,”J.Vib.Control,vol.16,no.11,pp.1701−1711,May2010.
17 C.Liu,C.D.Li,and S.K.Duan,“Stabilization of oscillating neural networks with time-delay by intermittent control,”Int.J.Control Autom.Syst.,vol.9,no.6,pp.1074−1079,Dec.2011.
18 S.C.Wu,C.D.Li,X.F.Liao,and S.K.Duan,“Exponential stability of impulsive discrete systems with time delay and applications in stochastic neural networks:a Razumikhin approach,” Neurocomputing,vol.82,29−36,Apr.2012.
19 J.Hu and J.Wang,“Global uniform asymptotic stability of memristor-based recurrent neural networks with time delays,”in Proc.2010 Int.Joint Conf.Neural Networks(IJCNN),Barcelona,Spain,pp.1−8.
20 G.D.Zhang,Y.Shen,and J.W.Sun,“Global exponential stability of a class of memristor-based recurrent neural networks with time-varying delays,”Neurocomputing,vol.97,pp.149−154,Nov.2012.
21 L.Zhang and Z.Yi,“Selectable and unselectable sets of neurons in recurrent neural networks with saturated piecewise linear transfer function,”IEEE Transactions on Neural Networks,vol.22,no.7,pp.1021−1031,Jul.2011.

22 M.Forti and P.Nistri,“Global convergence of neural networks with discontinuous neuron activations,”IEEE Trans.Circuits and Systems I:Fundamental Theory and Applications,vol.50,no.11,pp.1421−1435,Nov.2003.Yinlu Jiang received the B.S.degree in communication engineering from Southwest University of Science and Technology,Sichuan,China,in 2013,and presently she is studying for M.S.degree in Signal and Information Processing at Southwest University,Chongqing,China.Her research interests include neural networks,memristive systems,and impulsive dynamical systems.E-mail:jiang_yinlu@126.com

Yinlu Jiang and Chuandong Li.Globally exponential stability of memristive neural networks with time-varying delays and synchronous switching.Acta Automatica Sinica,2017,43(8):1465−1469
the B.S.degree in applied mathematics from Sichuan University,Chengdu,China in 1992,and M.S.degree in operational research and control theory and Ph.D.degree in computer software and theory from Chongqing University,Chongqing,China,in 2001 and 2005,respectively. He has been a Professor at the College of Electronic and Information Engineering,Southwest University,Chongqing,China,since 2012,and has been the IEEE Senior Member since 2010.From November 2006 to November 2008,he served as a Research Fellow in the Department of Manufacturing Engineering and Engineering Management,City University of Hong Kong,Hong Kong,China.He has published about more than 100 journal papers.His research interests include computational intelligence,neural networks,memristive systems,chaos control,and synchronization,and impulsive dynamical systems.Corresponding author of this paper.E-mail:licd@cqu.edu.cn
Manuscript
June 7,2015;accepted October 13,2015.
This work was supported by the National Natural Science Foundation of China(61374078)and Natural Science Foundation Project of Chongqing CSTC(cstc2014jcyjA40014).
Recommended by Associate Editor Zhanshan Wang.
1.College of Electronic and Information Engineering,Southwest University,Chongqing 400715,China
