Reliability-based Robust Optimization Design Based on Specular Re fl ection Algorithm
2017-09-11QisongQiJunWangGeningXuXiaoningFan
Qisong Qi Jun Wang Gening Xu Xiaoning Fan
Reliability-based Robust Optimization Design Based on Specular Re fl ection Algorithm
Qisong Qi1Jun Wang1Gening Xu1Xiaoning Fan1
In this paper,a novel global optimization method—specular re fl ection algorithm(SRA)is proposed,which simulates the unique optical property of mirror—re fl ection function.Combining the computing features of the SRA with traditional mathematical theories,the global convergence ability of the SRA is veri fi ed.The reasonable value of the SRA’s control parameter is analysed,so that the best control parameter which is suitable for current optimization problems can be acquired.Four numerical examples are researched using the SRA and other 4 classical intelligent optimization methods,such as particle swarm optimization,Kalman swarm optimization,etc.Simulation results of numerical examples demonstrated the e ff ectiveness and superiority of the SRA,especially its suitability for solving high dimensional,multi-peak complex functions.Finally the structure of general bridge crane is investigated and designed by SRA for robust reliability optimization design.The results illustrate that the SRA is reasonable,accurate and can be treated as an e ff ective analysis technique in reliability-based robust optimization design.It can be predicted that the SRA can be widely used in engineering for creating more value.
Engineering,mirror,robust reliability optimization,specular re fl ection algorithm(SRA)
DOI10.16383/j.aas.2017.e150129
1 Introduction
With the increasingly complicated engineering problems during the past few years,many researchers devote themselves to researching new intelligent optimization algorithms.In 2011,a new heuristic optimization algorithm named fruit fl y optimization algorithm(FOA)is proposed by Pan[1]who is inspired by the feeding behaviors of drosophila.FOA is easy to be understood,and it can deal with the optimization problems with fast speed and high accuracy,while,the results are in fl uenced a lot by the initial solutions[2].Based on the phototropic growth characteristics of plants,a new global optimization algorithm called plant growth simulation algorithm is proposed by Li et al.,which is a kind of bionic random algorithm and suitable for large-scale,multi-modal and nonlinear integer programming[3],however,for its complex calculation theory,the algorithm is not widely applied in industry and scienti fi c research.Arti fi cial bee colony algorithm[4]is a new application of swarm intelligence,which simulates the social behaviors of bees,whose defects are slow convergence speed and easy to trap into local optimum[5].
Mirror is a common necessity,which plays an important role in daily life.Inspired by the optical function of mirror,a new algorithm called specular re fl ection algorithm(SRA)is raised by this paper.SRA,similar to genetic algorithm[6]−[8],particle swarm optimization[9]−[11],simulated annealing algorithm[12],[13],di ff erential evolution algorithm[14],[15],etc,can be widely used in science and engineering.The SRA has many outstanding advantages,such as simple principle,easy programming,high precision and fast calculation speed,and its unique non-population searching mode distinguishes itself from original swarm algorithm.Furthermore,the global searching ability is signi fi cantly improved by the speci fi c acceptance criterion of the new solution.In order to verify above mentioned features of SRA,a great deal of comparative experiments are adopted in this paper.At last,the reliability based design and robust design arecombined with the SRA,in order to evaluate the ability of SRA in reliability based robust optimization design.
2 SRA
2.1 Introduction of SRA
Mirror is a life necessity and a product of human civilization,which can change the direction of propagation of light.There are various kinds of mirrors,such as magnifying glass,microscope,etc.With the help of mirror,a great deal of stu ffcan be observed,even if they are out of the range of visibility.For example,the submarine soldier is able to catch sight of the object above the water by periscope.This re fl ection property of mirror is simulated by the SRA.
Object,suspected target,eyes and mirror are the four basic elements of specular re fl ection system.
Object is the objective function of optimization.Getting its exact coordinate is the purpose of the SRA.It is not involved in the optimization procedure for the location of the object is unpredictable.
Suspected target is the coordinate of the object observed by eyes,which is approximate to the optimal solution.There is an error between the suspected target and object,because the coordinate of the object observed by eyes is not accurate.The suspected target is located around the object,and it is the element nearest to the object.
Mirror can change the direction of propagation of light.The vision of eyes can be broaden by mirror.All the things that can re fl ect light(glass,water,etc.)are taken as mirror.
Eyes are the subject of the SRA,which can acquire the approximate coordinate of the object.And it is the element farthest from the object.
2.2 De fi nition
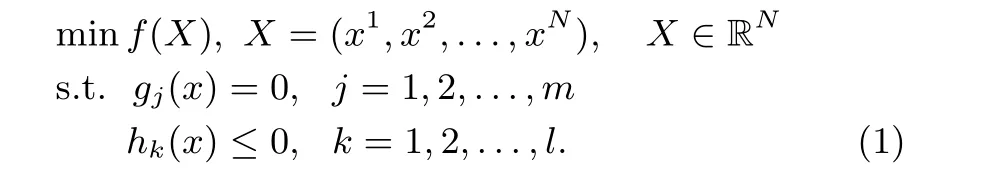
Taking the constrained optimization problem showed in(1)as an example,the de fi nition of SRA will be drawn as following:
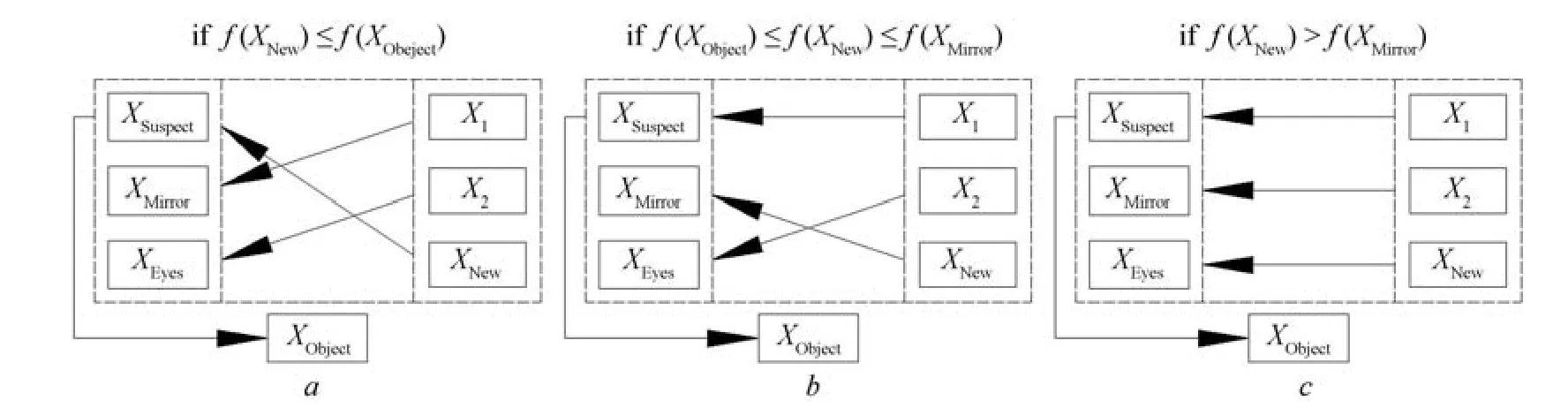
Fig.1. Coordinate update of the specular re fl ection system.
Set the specular re fl ection system as a 4×N dimensional Euclidean space,where N is the number of design variables.The elements in the system are de fi ned as,i=(0,1,2,3),and XObject=X0,XSuspect=X1,XMirror=X2,XEyes=X3.Where(n=1,2,...,N)is the position of the ith variable in the N dimensional space.The four elements of SRA can be de fi ned as f(Xi),and the relationship among the four elements is f(X0)≤f(X1)≤f(X2)≤f(X3).
Searching the new coordinate:the coordinates of XNew1and XNew2can be acquired by(2),and the new coordinate of XNewcan be got by(2).
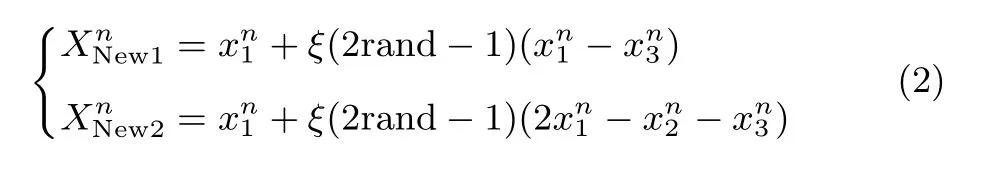
where ξ is coefficient,which is determined by(11).
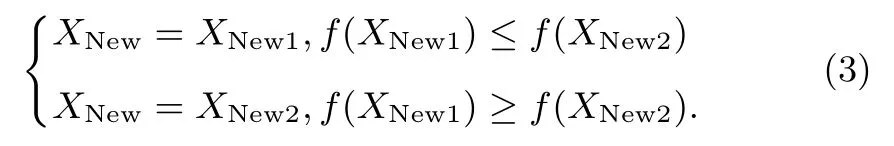
Updating the specular re fl ection system:Once the coordinate of XNewis acquired,the eyes will change its place to continue searching for the “object”,the four elements of the system are X0X1X2and XNewunder the current situation.The specular re fl ection system will be adjusted by the modi fi cation of the four elements,the system will be changed by the rules shown in Fig.1.
The optimization steps of the SRA are shown as follows:
Step 1:De fi ne the initial value Xi,i=0,1,2,3,and the maximum iteration number Itermax.
Step 2:If the precision or the maximum iteration number reaches the design requirements,the coordinate of XObjectwill be output which is the optimum solution.Otherwise,execute the next step continually.
Step 3:Search the coordinate of XNewby(2)and(3),the new iteration process will begin,then go back to Step 2 and Continue to calculate.
In conclusion,the optimization fl ow chart of the SRA is given by Fig.2.
2.3 Optimization Flow Chart of the SRA
Theorem 1:The constraint optimization problem presented in(1)can converge to the global extremum with 100%probability by the SRA.
Proof:Provided that XObject=minf(X),X∈D which is the global optimal solution,where f(XObject)is the optimal value of objective function,D is the feasible region and D={X|gj(XObject)=0,j=1,2,...,m;hk(XObject)≤0,k=1,2,...,l;XObject∈Rn}and D∈RN.
First,get the feasible initial solutionsandrandomly among the searching space,where,and the corresponding values of objective functioncan be worked out,where.

Fig.2. Optimization fl ow chart of the SRA.
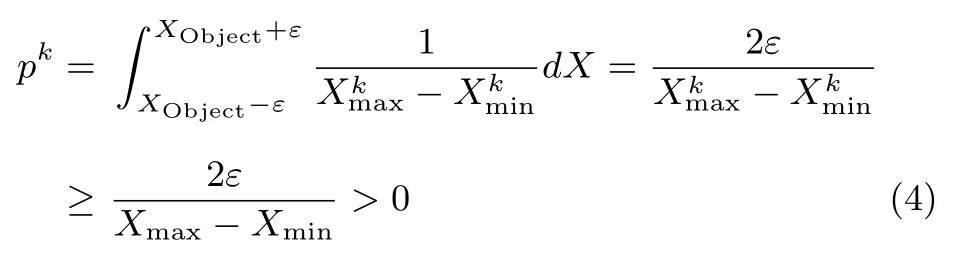
where ε is a real number which is sufficiently small;Xmaxand Xminare the extreme values of the 4×N dimensional Euclidean space.
The probability that the feasible solutionis optimal is P1,and the probability thatis not optimal is Q1,both P1and Q1are expressed as follows:

TABLE I JuDGEMENt oF ξ
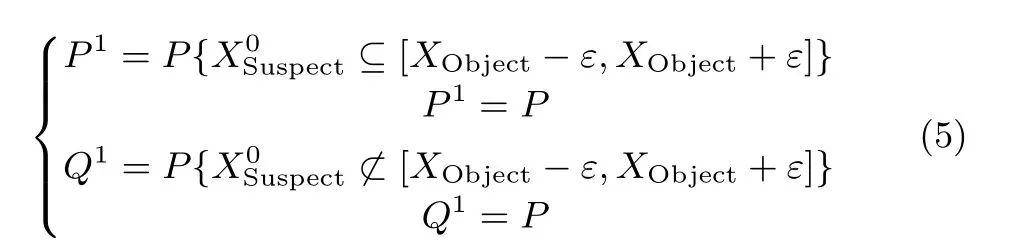
The probability that the feasible solution gotten for the second time still failing to be the optimal value is:

So,the probability that the solution is optimal is:
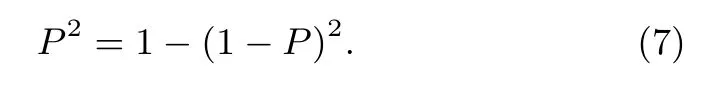
After n times iteration,the probability of getting the optimum solution can be acquired by the following inference.

Calculate the extreme value of(8):
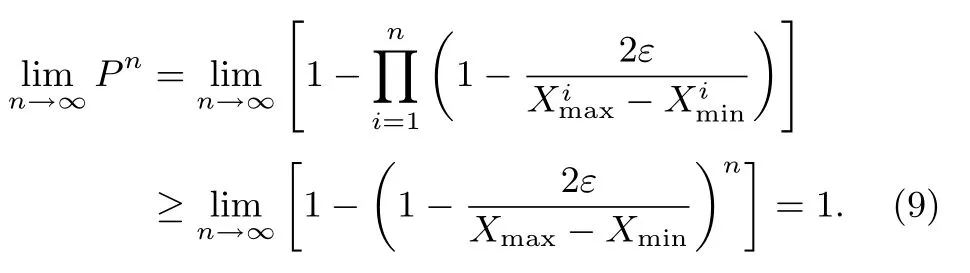
With the iterations going on,it is more and more likely to achieve the optimum solution.When n→∞,Pn→1,it indicates that the searching process of SRA can converge to the global extreme with 100%probability.
2.4 Selection of Control Parameter
The control parameter is closely related to the space complexity of optimized target,which has an e ff ect on the capability of algorithm.The control parameters of classical optimization algorithm are gotten by experience or experiment,such as the learning parameter c1=c2=2 by PSO[16],[17],and the crossover probability and mutation probability of GA[18].It is impossible that the control parameter acquired by experience is suitable for all optimization problems.The SRA only has the control parameter ξ,whose value will have a prominent e ff ect on SRA.In this section,a classical test function is used to con fi rm the most appropriate value of ξ,and the results are listed in Table I.

The test function is illustrated by(10),and its threedimension diagram is shown in Fig.3.The global minimum value in theory of this function is 0(0,0,...,0)and the constraint condition is−5.12≤xj≤5.12,j=1,2,...,N.In consideration of N=(2,10,20,50,100,500)and ξ=(0.4,0.5,...,2.0),do the calculation 50 times using every possible combination of N and ξ,then put the average results in Table I.Assume that the convergence condition is Itermax=105or f(x1,x2,...,xN)≤ 10−5.
As shown in Table I,all the results fall in between 10−5and 10−6,the optimization efficiency which is in fl uenced by ξ cannot be evaluated by the optimal solutions,therefore,iteration times is the only factor to be considered.
According to the Table I,the conclusions can be drawn as follows:when N=2 and ξ=1.9,the efficiency of the optimization is highest,the corresponding iteration is 82.44;When N=10,N=20,N=50 and N=100,the best ξ and its corresponding iteration times are 1.3 and654.72,1.1 and 1.2946×103,0.9 and 4.2036×103,0.7 and 1.0679 × 104,respectively.In addition,the value of ξ will be reduced gradually with the increasing of N,and the relationship between ξ and N(as shown in(11))can be speculated by the method of data fi tting.


Fig.3. Three-dimensional surface of test function.
2.5 Simulation Experiments
To verify the global optimization ability of SRA,four numerical test functions in[10]are used,each test function is listed in Table II in detail.The total iteration time is set as 2000.The SRA will be executed 50 times,and the average values are listed in Table III,other results are references from[10],Figs.4−7 show the iteration curves of the objective functions of each test function respectively.
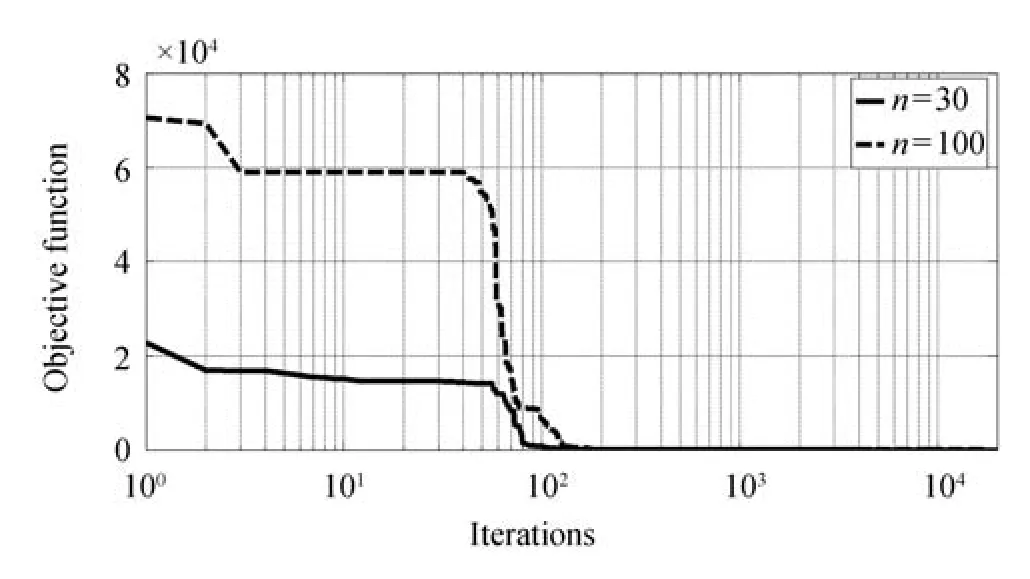
Fig.4. Iteration curve of sphere.
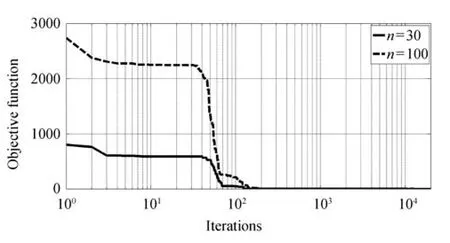
Fig.5. Iteration curve of griewank.
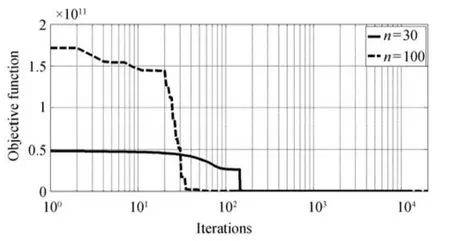
Fig.6. Iteration curve of rosenbrock.
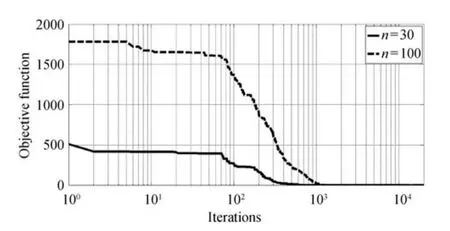
Fig.7. Iteration curve of restrigin.
The results in Table IV indicate that:when n=30,the results of the four test functions calculated by SRA are 1.1080×10−24,4.6629×10−15,9.8730×10−7and 3.9373 ×10−21respectively,which are 1.87×1015,2.12×104,2.90×102,1.11×1017times higher than the results gotten by new chaos PSO algorithm which possesses the highest accuracy in[10];When n=100,the results of the four test functions calculated by SRA are 2.3160×10−12,2.7978×10−14,6.1173× 10−5,8.7727×10−7respectively,and the computational accuracy are still 8.95×102,3.54×103,4.75,4.99×102times higher than the results calculated by new chaos PSO algorithm.All in all,the SRA is an efficient optimization algorithm.
3 Reliability Robust Optimization Design
3.1 Reliability Design
According to the reliability design theory,the reliability can be calculated by(12):
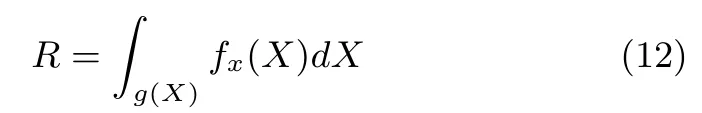
where fx(X)is the joint probability density of basic random variables X=(X1,X2,...,Xn)T,which shows the state of the components.

The basic random variables Xi(i=1,2,...,n)are independent of each other and follow certain distribution.The reliability index β and the reliability R= Φ(·)can be calculated by Monte Carlo method[19],where Φ(·)is the standard normal distribution function.

TABLE II NuMERiCAL CALCuLAtioN FuNCtioN
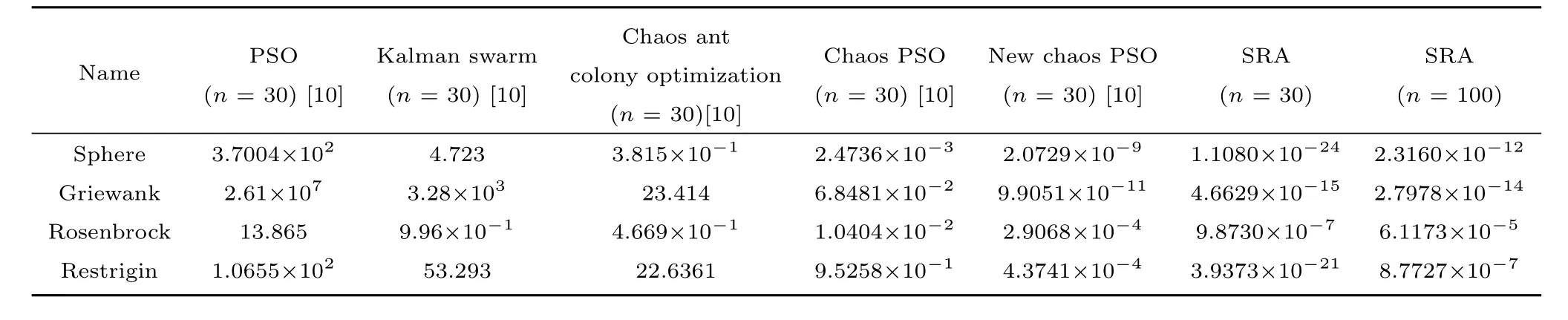
TABLE III CALCuLAtioN REsuLts oF TEst FuNCtioN
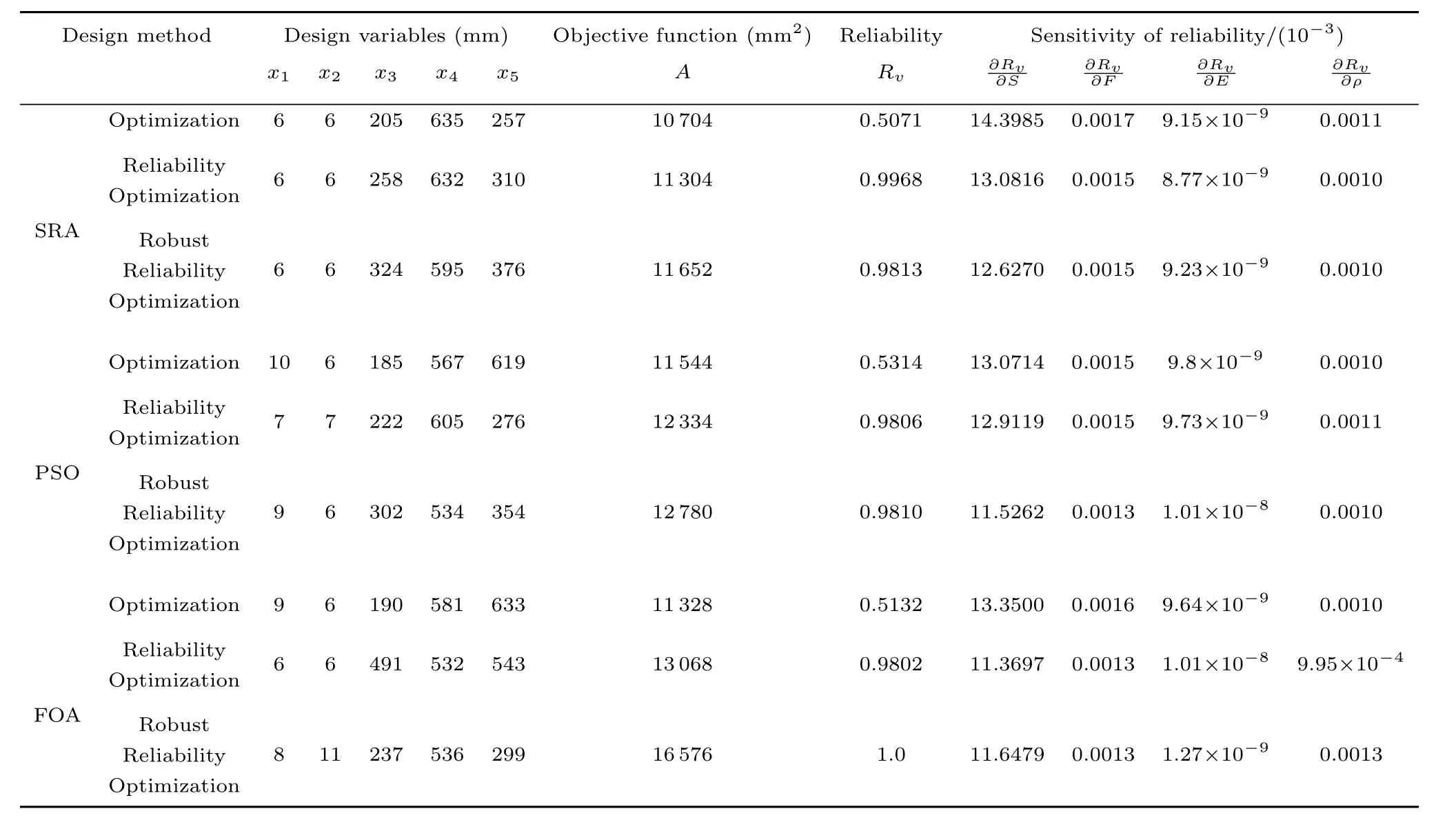
TABLE IV CALCuLAtioN REsuLts
3.2 Reliability Robust Optimization Design
Robust design is a modern design technique that can improve the efficiency and quality and reduce the cost of products[20],[21].The robust design of mechanical products can make the products insensitive to the changes of design parameters.The product which is designed by robust design method has the characteristic of stability.Even if there is an error in the designed parameters,the product still has excellent performance.Reliability is a kind of design method to eliminate the weaknesses,failure modes and guard against malfunction.The reliability robust optimization design is a new method by combining the robust design and reliability design,which possess all the merits of the two methods.The products designed by the reliability robust optimization design method are reliable and haverobustness.

where f1(X)and f2(X)are the objective functions of the Reliability Robust Optimization design,f1(X)=R and f2(X)is the design criterion related to robust design which can be acquired by(15);R is the reliability;R0is the constraint condition of reliability;piand qjare equality and inequality constraints of the robust reliability optimization design respectively.

where ω1and ω2are weighting coefficients,which are related to the importance of f1(X)and f2(X),both of them are calculated by(16),and ω1+ ω2=1.

where X1∗and X2∗are the best values when minf(X)=f1(X)and minf(X)=f2(X)respectively.
4 Engineering Example
The bridge crane is taken as an example to verify the capability of the SRA in solving the engineering problems.The SRA is adopted to design the structure with optimized design,reliability optimization design and robust reliability optimization design,and the results are listed in Table III together with the results calculated by PSO and FOA,which are used for analysing the performance of the SRA.
4.1 Design Parameters
The mechanical model of the bridge crane is shown in Fig.8,the uniform load q and the concentrated load F are exerted on the girder,where q is caused by the structure deadweight and F is related to the weight of the hoisted cargo.
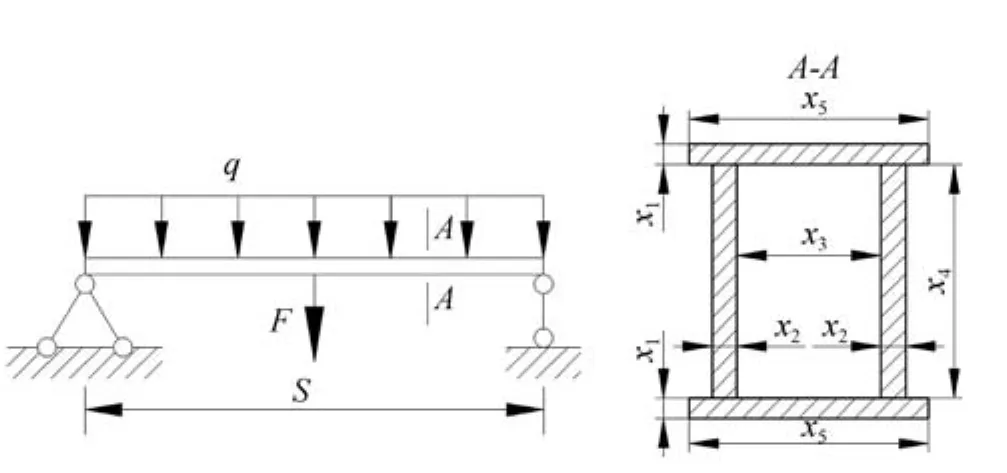
Fig.8.Mechanical model diagram and sectional dimension.
The parameters xi(i=1,2,3,4,5)are considered to be the design variables,where 6≤x1,x2≤30,50≤x3,x4≤5000,x5=x3+2x2+40.The parameter S is the span of the bridge crane.Other parameters include the elasticity modulus E,the material density ρ,q=g(x1,x2,x3,x4,x5). The parameters S,F,E and ρ are independent of each other,and they are normal random variables,S~N(12,0.082),F~N(92100,4652),E~N(206000,61802),ρ~ N(7850,5.62).
4.2 Optimization Design
Objective function:According to the characteristics of the structural optimization problem,the objective function can be de fi ned as shown in(17).

Constraint condition:Strength,sti ff ness and stability are the three basic failure modes of bridge crane.Therefore,the constraint condition can be de fi ned as following:
1)Strength Constraint:The maximum stress of dangerous point in mid-span section must be smaller than the ultimate stress frd;

where frdis determined by the limit state method,and frd=fyk/γm=235/1.1=213.64MPa,f(yk)=235 is yield stress,γm=1.1 is the resistance coefficient,IZis moment of inertia of Section 2.1,q and IZare the functions related to design variables xi(i=1,2,3,4,5).
2)Sti ff ness Constraint:The maximum de fl ection of the structure must be smaller than the allowable value γ0=S/400.

3)Stability Constraint:The depth-width ratio of Section 2.1 must be smaller than 3.
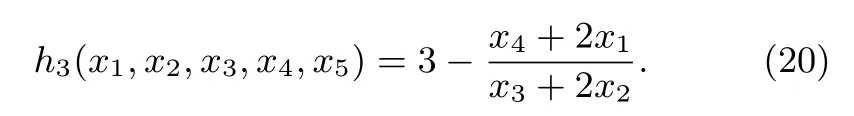
In conclusion,the optimization model of the bridge crane can be built as(21).
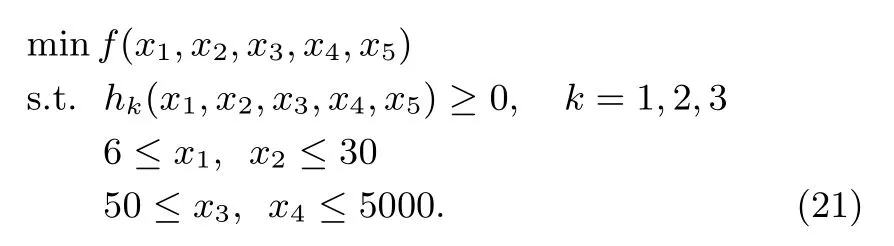
4.3 Reliability Optimization Design
The reliability constraint of structure is added to(21)to achieve the reliability optimization design.The failure of any mode will result in the failure of the structure,so the reliability Rvis de fi ned by(22).The reliability optimization model of bridge crane can be established by(23).

where Rk,k=1,2,3 is the probability of the kth failure mode.
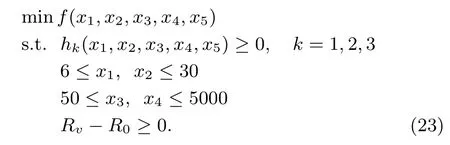
4.4 Robust Reliability Optimization Design
According to the robust reliability optimization design model which is shown in(14),the index of reliability and robustness are taken into account,the multi-objective optimization model is built by(24).

4.5 Calculation Results
The three optimization models shown in(21),(23)and(24)are calculated by the SRA,PSO and FOA,respectively.And the results are presented in Table III,from which the conclusions can be drawn as follows:
1)For structural optimization,the results obtained by the three algorithms are 10704,11544 and 11328,the optimum among the three is 10704 which is calculated by the SRA,which proves the ability of SRA is higher than PSO and FOA.The reliability results of the three groups of parameters are 0.5071,0.5314 and 0.5132 respectively,which are unable to meet the requirement of reliability design for the reliability constraint is ignored.
2)The reliability of the structure can be ensured and the robustness can be improved after reliability optimization design.However,the areas of Section 2.1 are increased to 11652,12334 and 16576 at the same time,and the best result is also calculated by SRA.
3)With the requirements of the robustness,the reliability sensitivity index of design variables are signi fi cantly reduced,and the robustness of structure is improved notably.
5 Conclusions
In this paper,a new optimization algorithm—specular re fl ection algorithm(SRA)is proposed,which is inspired by the optical property of the mirror.The SRA has a particular searching strategy which is di ff erent from the swarm intelligence optimization algorithms.The convergence ability of the SRA is veri fi ed by the traditional mathematical method,it converges to the global optimum value with the probability of 100%.The reasonable values of the control parameters are analysed,and their computational formula is deduced by the method of data fi tting,so that the control parameters will vary with the di ff erent problems and thus the adaptation and the operability of the SRA will be improved.Four classical numerical test functions are analysed by the SRA,and the results indicate that the ability of the SRA is better than the traditional intelligent optimization algorithms.Then,the theories of the reliability optimization and robust design are combined to establish the mathematical models of the optimization design,reliability optimization design and robust reliability optimization design for the bridge crane as an example system,which are calculated by the SRA and other two optimization methods(PSO and FOA).The conclusions are drawn after the simulation,that the structure designed by the SRA is reliable and robust.The results calculated by the SRA are superior to the PSO and the FOA.All in all,the SRA is the latest research in the area of intelligent optimization,which has the better calculation capability than other optimization algorithms,and the ability for the structure design is veri fi ed in this paper.SRA can be widely applied in other fi elds and create more value.
1 W.T.Pan,“A new fruit fl y optimization algorithm:Taking the fi nancial distress model as an example,”Knowl.Based Syst.,vol.26,pp.69−74,Feb.2012.
2 H.Cheng and C.Z.Liu,“Mixed fruit fl y optimization algorithm based on chaotic mapping,”Comput.Eng.,vol.39,no.5,pp.218−221,May 2013.
3 T.Li,C.F.Wang,W.B.Wang,and W.L.Su,“A global optimization bionics algorithm for solving integer programming-Plant growth simulation algorithm,”Syst.Eng.Theory Pract.,vol.25,no.1,pp.76−85,Jan.2005.
4 D.Karaboga and B.Basturk,“On the performance of arti ficial bee colony(ABC)algorithm,”Appl.Soft Comput.,vol.8,no.1,pp.687−697,Jan.2008.
5 X.J.Bi and Y.J.Wang,“A modi fi ed arti fi cial bee colony algorithm and its application,”J.Harbin Eng.Univ.,vol.33,no.1,pp.117−123,Jan.2012.
6 J.H.Holland,Adaptation in Natural and Arti fi cial Systems.Ann Arbor,MI:University of Michigan Press,1975.
7 M.Franchini,“Use of a genetic algorithm combined with a local search method for the automatic calibration of conceptual rainfall-runo ffmodels,”Hydrol.Sci.J.,vol.41,no.1,pp.21−39,Feb.1996.
8 C.Y.Liu,C.Q.Yan,J.J.Wang,and Z.H.Liu,“Particle swarm genetic algorithm and its application,”Nucl.Power Eng.,vol.33,no.4,pp.29−33,Aug.2012.
9 L.B.Zhang,C.G.Zhou,M.Ma,and X.H.Liu,“Solutions of multi-objective optimization problems based on particle swarm optimization,”J.Comput.Res.Dev.,vol.41,no.7,pp.1286−1291,Jul.2004.
10 X.B.Xu,K.F.Zheng,D.Li,M.Ma,and Y.X.Yang,“New chaos-particle swarm optimization algorithm,”J.Commun.,vol.33,no.1,pp.24−30,37,Jan.2012.
11 H.Modares,A.Al fi,and M.B.Naghibi Sistani,“Parameter estimation of bilinear systems based on an adaptive particle swarm optimization,”Eng.Appl.Artif.Intell.,vol.23,no.7,pp.1105−1111,Oct.2010.
12 S.Kirkpatrick,C.D.Gelatt Jr,and M.P.Vecchi,“Optimization by simulated annealing,”Science,vol.220,no.4598,671−680,May 1983.
13 K.Abdi,M.Fathian,and E.Safari,“A novel algorithm based on hybridization of arti fi cial immune system and simulated annealing for clustering problem,”Int.J.Adv.Manuf.Technol.,vol.60,no.5−8,pp.723−732,May 2012.
14 R.Storn and K.Price,“Di ff erential evolution-A simple and efficient heuristic for global optimization over continuous spaces,” J.Global Optim.,vol.11,no.4,pp.341−359,Dec.1997.
15 B.V.Babu and M.M.L.Jehan,“Di ff erential evolution for multi-objective optimization,”in Proc.The 2003 Congress on Evolutionary Computation,Canberra,ACT,Australia,vol.4,pp.2696−2703,Dec.2003.
16 Z.X.Liu and H.Liang,“Parameter setting and experimental analysis of the random number in particle swarm optimization algorithm,”Control Theory Appl.,vol.27,no.11,pp.1489−1496,Nov.2010.
17 C.K.Dimou and V.K.Koumousis,“Reliability-based optimal design of truss structures using particle swarm optimization,” J.Comput.Civil Eng.,vol.23,no.2,pp.100−109,Mar.2009.
18 D.A.McAdams and W.Li,“A novel method to design and optimize fl at-foldable origami structures through a genetic algorithm,”J.Comput.Inform.Sci.Eng.,vol.14,no.3,Article ID:031008,Jun.2014.
19 Z.Z.Lv,S.F.Song,H.S.Li,and X.K.Yuan,Structure and Mechanism Reliability Analysis and Reliability Sensitivity Analysis.Beijing,China:Science Press,2009.
20 H.X.Guo,“Current status of research on robust design and development of research on fuzzy robust design,”J.Mach.Design,vol.22,no.2,pp.1−5,Feb.2005.
21 Y.M.Zhang,R.Y.Liu,and F.H.Yu,“Multi-objective reliability based on robust optimization design for vehicle frontaxles,” Mach.Design and Res.,vol.22,no.4,pp.82−84,106,Aug.2006.

Qisong QiisaPh.D.candidateat Taiyuan University of Science and Technology,China.His research interests include intelligent optimization algorithm,structure reliability design and structure design of Crane.Corresponding author of this paper.E-mail:qiqisong_19870328@126.com

Jun Wang isaPh.D.candidateat Taiyuan University of Science and Technology,China.Her research interests include intelligent optimization algorithm and hydraulic servo control system.
E-mail:best-wangj@126.com


Xiaoning Fan received the Ph.D.degree from Dalian University of Technology,China.She is currently a Professor of Taiyuan University of Science and Technology.Her research interests include computational intelligence,optimization design and structure fatigue life evaluation.
E-mail:fannyfxn@163.com
Qisong Qi,Jun Wang,Gening Xu,Xiaoning Fan.Reliability-based robust optimization design based on specular re fl ection algorithm.Acta Automatica Sinica,2017,43(8):1457−1464
the Ph.D.degree from Tongji University,China.He is currently a Professor of Taiyuan University of Science and Technology.His research interests include theory and method of structure design and analysis and structure reliability design.E-mail:xugening@sina.com
Manuscript
August 4,2015;accepted February 1,2016.
This work was supported by the National Natural Science Foundation of China(51275329).
Recommended by Associate Editor Qinglai Wei.
1.Taiyuan University of Science and Technology,Taiyuan 030024,China
